Функция это способы представления функций

4. графический. Графический способ – самый удобный для наглядного представление функции и её свойств. Для графического способа представления функции используют декартову систему координат.

Источник

Что такое Функция?

О чем эта статья:

7 класс, 11 класс, ЕГЭ/ОГЭ

Понятие функции

Определение функции можно сформулировать по-разному. Рассмотрим несколько вариантов, чтобы усвоить наверняка.

1. Функция — это взаимосвязь между величинами, то есть зависимость одной переменной величины от другой.

Знакомое обозначение y = f (x) как раз и выражает идею такой зависимости одной величины от другой. Величина у зависит от величины х по определенному закону, или правилу, которое обозначается f.

Вывод: меняя х (независимую переменную, или аргумент) — меняем значение у.

2. Функция — это определенное действие над переменной.

Значит, можно взять величину х, как-то над ней поколдовать — и получить соответствующую величину у.

В технической литературе можно встретить такие определения функции для устройств, в которых на вход подается х — на выходе получается у. Схематично это выглядит так:

В этом значении слово «функция» используют и в далеких от математики областях. Например, так говорят о функциях ноутбука, костей в организме или даже о функциях менеджера в компании. В каждом перечисленном случае речь идет именно о неких действиях.

3. Функция — это соответствие между двумя множествами, причем каждому элементу первого множества соответствует один элемент второго множества. Это самое популярное определение в учебниках по математике.

Например, в функции у = 2х каждому действительному числу х ставит в соответствие число в два раза большее, чем х.

Область определения — множество х, то есть область допустимых значений выражения, которое записано в формуле.

Например, для функции вида

область определения выглядит так:

• х ≠ 0 (потому что на ноль делить нельзя)

И записать это можно так: D (y): х ≠ 0.

Область значений — множество у, то есть это значения, которые может принимать функция.

Например, естественная область значений функции y = x2 — это все числа больше либо равные нулю. Можно записать вот так: Е (у): у ≥ 0.

Для примера рассмотрим соответствие между двумя множествами — человек-владелец странички в инстаграм и сама страничка, у которой есть владелец. Такое соответствие можно назвать взаимно-однозначным — у человека есть страничка, и это можно проверить. И наоборот — по аккаунту в инстаграм можно проверить, кто им владеет.

В математике тоже есть такие взаимно-однозначные функции. Например, линейная функция у = 3х +2. Каждому значению х соответствует одно и только одно значение у. И наоборот — зная у, можно сразу найти х.

Источник

Определение функции. Способы задания функции.

Что значить задать функцию? Какими способами можно задать функцию? Что такое определение функции?

Задать функцию — это значит указать правило, при задании любого значения аргумента x вы найдете значение функции y.

Функция y=f(x) – зависимость переменной y от переменной x. Когда задаем значение аргумента x, получаем единственное значение функции y.

Способы задания функции.

В данной статье рассмотрим 3 способа задания функции. На самом деле их больше, в школьной программе чаще всего разбирают эти способы задания функции.

Аналитический способ задания функции.

Чаще всего в школьной программе правило задают в виде формулы y=f(x), x∈X или нескольких формул. Такой способ задания функции называется аналитическим.

Примеры аналитического задания функции:

Графический способ задания функции.

Также если по формуле построить график функции, то данный способ задания функции будет называться графическим. Не всегда вам будут давать график совместно с формулой. Иногда вам в заданиях будут давать только график функции, по которому вы должны будете найти определенные данные. По графику функции можно восстановить его формулу, но это не всегда легко сделать, все зависит от начерченного графика. В школьной программе вам будут задавать графики, по которым вы сможете рассчитать формулу.

Примеры, графического задания функции:

Табличный способ задания функции.

Следующий способ задания функции применяется чаще всего на практике называется табличный.

Все данные представлены в виде таблице. У этого способа имеется конечное множество значений аргумента. Такими таблицами вы уже пользовались в алгебре, например, таблица квадратов, таблица корней и т.д.

Примеры, табличного задания функции:

Рассмотрим примеры по теме «Способы задания функции»:

Пример №1:

Является ли графическим заданием какой-либо функции фигура?

Сколько бы мы не проводили вертикальных линий, всегда будет одно пересечение с графиком. Следовательно, изображенная фигура является графиком функции.

Пример №2:

Является ли графическим заданием какой-либо функции фигура?

Сколько бы мы не проводили вертикальных линий, всегда будет одно пересечение с графиком. Следовательно, изображенная фигура является графиком функции.

Пример №3:

Является ли графическим заданием какой-либо функции фигура?

При проведении вертикальных линий у нас имеется два пересечения. То есть у одной вертикальной линии два пересечения с фигурой. По определению переменной x должно соответствовать только одно значение переменной y, а у нас два пересечения фигуры. Следовательно, данная фигура не является графиком функции.

Источник

Функция (математика)

Из Википедии — свободной энциклопедии

Фу́нкция (отображе́ние, опера́тор, преобразова́ние) в математике — соответствие между элементами двух множеств — правило, по которому каждому элементу первого множества соответствует один и только один элемент второго множества.

Математическое понятие функции выражает интуитивное представление о том, как одна величина полностью определяет значение другой величины. Так, значение переменной x <\displaystyle x> однозначно определяет значение выражения x 2 <\displaystyle x^<2>> , также значение месяца однозначно определяет значение следующего за ним месяца. «Житейский» пример функции: каждому человеку можно однозначно поставить в соответствие его биологического отца.

Аналогично, заранее заданный алгоритм по значению входного данного выдаёт значение выходного данного.

Часто под термином «функция» понимается числовая функция, то есть функция, которая ставит одни числа в соответствие другим. Эти функции удобно представлять в виде графиков.

Источник

Вопрос 1.

Функция — переменная величина у называется функцией переменной величины х(аргумент или независимая переменная), если каждому допустимому значению х соответствует определенное и единственной значение у: у= f(х). совокупность допустимых значений аргумента х называется областью определения функции. Способы представлений функций:

аналитический – в виде уравнения или формулы: у = f(х) При аналитическом задании функции часто не указывают область ее определения. Если функция задана формулой, то при отсутствии особых оговорок областью ее определения считается наибольшее множество, на котором эта формула имеет смысл.. Например, функция спроса задана уравнением: Q=30 — 8P;

Графиком функции называется множество точек плоскости, абсциссами которых служат значение аргумента х, а ординатами – соответствующие им значения функции у. Графический способ задания функции используют тогда, когда функцию трудно или невозможно задать аналитически. График функции дает наглядное представление о свойствах функции. Задать функцию графически — это значит построить ее график

При табличном способе задания функции рядом с числовым значением аргумента выписывается соответствующее значение функции. Таблицы могут составляться также по значениям х и у, полученным из опыта или наблюдения. Недостатком табличного способа задания функции является то, что в таблице могут быть указаны не все, а лишь отдельные значения аргумента и функции. Особенности изменения функции при этом могут быть искажены или утрачены.

Непрерывные функции. Непрерывная функция — функция без «скачков», то есть такая, у которой малые изменения аргумента приводят к малым изменениям значения функции. Функция у= f(х). называется непрерывной при данном значении х=х₀, если бесконечно малому приращению ∆х аргумента х соответствует бесконечно малое приращение функции ∆у, т.е. выполняется условие

Вопрос 2

Переменные величины — это такие величины, которые в условиях данного вопроса могут принимать различные значении. Постоянные величины — это такие величины, которые в условиях данного вопроса сохраняют неизменные значения. Одни и те же величины в условиях одного вопроса могут быть постоянными, а в другом переменными.Например Температура T кипения воды в большинстве физических вопросов — величина постоянная T=100°C. Однако в тех вопросах, где нужно считаться с изменением атмосферного давления, T величина переменная.Различие постоянных и переменных величин особенно часто применяется в высшей математике. В элементарной математике основную роль играет разделение величин на известные и неизвестные. Последнее сохраняется и в высшей математике, но не играет там основной роли. Переменные величины как правило обозначаются последними буквами латинского алфавита x, y, z. А постоянные — первыми a, b, c.Бесконечно малые и бесконечно большие величины.Понятие бесконечно малых и бесконечно больших величин играет важную роль в математическом анализе. Многие задачи просто и легко решаются используя понятия бесконечно больших и малых величин.Бесконечно малые. 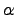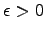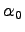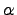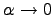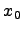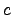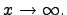Переменная называется бесконечно малой, если для любого существует такое значение , что каждое следующии за ним значение будет по абсолютной величине меньше .Если — бесконечно малая то говорят, что стремится к нулю, и пишут: .Бесконечно большие.Переменная x называется бесконечно большой, если для всякого положительного числа cсуществует такое значение , что каждое следующее за ним x будет по абсолютной величине больше . Пишут: Величина, обратная к бесконечно большой, есть величина бесконечно малая, и обратно.

Теорема 1. Алгебраическая сумма двух, трех и вообще любого конечного числа бесконечно малых есть функция бесконечно малая.

Доказательство. Приведем доказательство для двух слагаемых. Пусть f(x)=α(x)+β(x), где 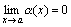и . Нам нужно доказать, что при произвольном как угодно малом ε>0 найдется δ>0, такое, что для x, удовлетворяющих неравенству |x – a| 0. Так как по условию теоремы α(x) – бесконечно малая функция, то найдется такое δ₁>0, что при |x – a| 0, что при |x – a| 0 найдется окрестность точки a, в которой будет выполняться неравенство |α(x)| 1 / 37 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 > Следующая > >>

Тут вы можете оставить комментарий к выбранному абзацу или сообщить об ошибке.

Источник