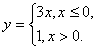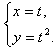Функции способы задания функций ответы

Функция. Способы задания функций.

Функция является заданной, иначе говоря, известной, если для каждого значения возможного числа аргументов можно узнать соответствующее значение функции. Наиболее распространенные три способа задания функции: табличный, графический, аналитический, существуют еще словесный и рекурсивный способы.

1. Табличный способ наиболее широко распространен (таблицы логарифмов, квадратных корней), основное его достоинство – возможность получения числового значения функции, недостатки заключаются в том, что таблица может быть трудно читаема и иногда не содержит промежуточных значений аргумента.

Аргумент х принимает заданные в таблице значения, а у определяется соответственно этому аргументу х.

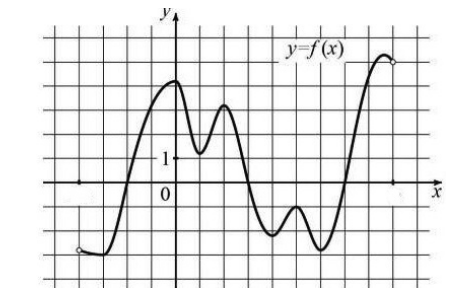
2. Графический способ заключается в проведении линии (графика), у которой абсциссы изображают значения аргумента, а ординаты – соответствующие значения функции. Часто для наглядности масштабы на осях принимают разными.

Например: для нахождения по графику у, которому соответствует х = 2,5 необходимо провести перпендикуляр к оси х на отметке 2,5. Отметку можно довольно точно сделать с помощью линейки. Тогда найдем, что при х = 2,5 у равно 7,5, однако если нам необходимо найти значение у при х равном 2,76, то графический способ задания функции не будет достаточно точным, т.к. линейка не дает возможности для столь точного замера.

Достоинства этого способа задания функций заключаются в легкости и целостности восприятия, в непрерывности изменения аргумента; недостатком является уменьшение степени точности и сложность получения точных значений.

3. Аналитический способ состоит в задании функции одной или несколькими формулами. Основным достоинством этого способа является высокая точность определения функции от интересующего аргумента, а недостатком является затрата времени на проведение дополнительных математических операций.

Функцию можно задать с помощью математической формулы y=x 2 , тогда если х равно 2, то у равно 4, возводим х в квадрат.

4. Словесный способ состоит в задании функции обычным языком, т.е. словами. При этом необходимо дать входные, выходные значения и соответствие между ними.

Словесно можно задать функцию (задачу), принимающуюся в виде натурального аргумента х с соответствующим значением суммы цифр, из которых состоит значение у. Поясняем: если х равно 4, то у равно 4, а если х равно 358, то у равен сумме 3 + 5 + 8, т. е 16. Далее аналогично.

5. Рекурсивный способ состоит в задании функции через саму себя, при этом значения функции определяются через другие ее же значения. Такой способ задания функции используется в задании множеств и рядов.

При разложении числа Эйлера задается функцией:

Ее сокращение приведено ниже:

При прямом расчёте возникает бесконечная рекурсия, но можно доказать, что значение f(n) при возрастании n стремится к единице (поэтому, несмотря на бесконечность ряда, значение числа Эйлера конечно). Для приближённого вычисления значения e достаточно искусственно ограничить глубину рекурсии некоторым наперёд заданным числом и по достижении его использовать вместо f(n) единицу.

Источник

Понятие функции. Способы задания функции

Функцией называется закон, по которому числу х из заданного множества Х, поставлено в соответствие только одно число у, пишут 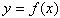, при этом x называют аргументом функции, y называют значением функции.

Существуют разные способы задания функций.

1. Аналитический способ.

Аналитический способ — это наиболее часто встречающийся способ задания функции.

Заключается он в том, что функция задается формулой, устанавливающей, какие операции нужно произвести над х, чтобы найти у. Например .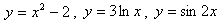

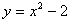
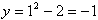
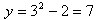
Рассмотрим первый пример — . Здесь значению x = 1 соответствует , значению x = 3 соответствует и т. д.

Функция может быть задана на разных частях множества X разными функциями.

Во всех ранее приведенных примерах аналитического способа задания, функция была задана явно. То есть, справа стояла переменная y, а слева формула от переменной х. Однако, при аналитическом способе задания, функция может быть задана и неявно.

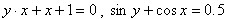
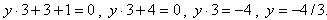
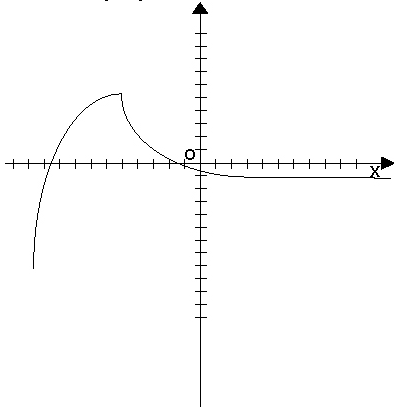
Например . Здесь, если мы задаем переменной x значение, то, чтобы найти значение переменной у (значение функции), мы должны решить уравнение. Например, для первой заданной функции при х = 3, будем решать уравнение:

. То есть, значение функции при х = 3 равно -4/3.

При аналитическом способе задания, функция может быть задана параметрически — это, когда х и у выражены через некоторый параметр t. Например,

Здесь при t = 2, x = 2, y = 4. То есть, значение функции при х = 2 равно 4.

2. Графический способ.

При графическом способе вводится прямоугольная система координат и в этой системе координат изображается множество точек с координатами (x,y). При этом 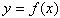. Пример:

3. Словесный способ.

Функция задается с помощью словесной формулировки. Классический пример – функция Дирихле.

«Функция равна 1, если х – рациональное число; функция равна 0, если х – иррациональное число».

4. Табличный способ.

Табличный способ наиболее удобен, когда множество Х конечно. При этом способе составляется таблица, в которой каждому элементу из множества Х, ставится в соответствие число Y.

Ошибка в тексте? Выдели её мышкой и нажми

Остались рефераты, курсовые, презентации? Поделись с нами — загрузи их здесь!

Источник

Что такое Функция?

О чем эта статья:

7 класс, 11 класс, ЕГЭ/ОГЭ

Понятие функции

Определение функции можно сформулировать по-разному. Рассмотрим несколько вариантов, чтобы усвоить наверняка.

1. Функция — это взаимосвязь между величинами, то есть зависимость одной переменной величины от другой.

Знакомое обозначение y = f (x) как раз и выражает идею такой зависимости одной величины от другой. Величина у зависит от величины х по определенному закону, или правилу, которое обозначается f.

Вывод: меняя х (независимую переменную, или аргумент) — меняем значение у.

2. Функция — это определенное действие над переменной.

Значит, можно взять величину х, как-то над ней поколдовать — и получить соответствующую величину у.

В технической литературе можно встретить такие определения функции для устройств, в которых на вход подается х — на выходе получается у. Схематично это выглядит так:

В этом значении слово «функция» используют и в далеких от математики областях. Например, так говорят о функциях ноутбука, костей в организме или даже о функциях менеджера в компании. В каждом перечисленном случае речь идет именно о неких действиях.

3. Функция — это соответствие между двумя множествами, причем каждому элементу первого множества соответствует один элемент второго множества. Это самое популярное определение в учебниках по математике.

Например, в функции у = 2х каждому действительному числу х ставит в соответствие число в два раза большее, чем х.

Область определения — множество х, то есть область допустимых значений выражения, которое записано в формуле.

Например, для функции вида

область определения выглядит так:

• х ≠ 0 (потому что на ноль делить нельзя)

И записать это можно так: D (y): х ≠ 0.

Область значений — множество у, то есть это значения, которые может принимать функция.

Например, естественная область значений функции y = x2 — это все числа больше либо равные нулю. Можно записать вот так: Е (у): у ≥ 0.

Для примера рассмотрим соответствие между двумя множествами — человек-владелец странички в инстаграм и сама страничка, у которой есть владелец. Такое соответствие можно назвать взаимно-однозначным — у человека есть страничка, и это можно проверить. И наоборот — по аккаунту в инстаграм можно проверить, кто им владеет.

В математике тоже есть такие взаимно-однозначные функции. Например, линейная функция у = 3х +2. Каждому значению х соответствует одно и только одно значение у. И наоборот — зная у, можно сразу найти х.

Источник

Функции и способы задания функций

Вы будете перенаправлены на Автор24

Определение функции

Существуют множество определений для понятия «функция».

Одними из классических определений понятия «функция» считаются определения на базе соответствий. Приведем ряд таких определений.

Зависимость, при которой каждому значению независимой переменной соответствует единственное значение зависимой переменной, называется функцией.

Пусть даны два непустых множества $X$ и $Y$. Соответствие $f$, которое каждому $x\in X$ сопоставляет один и только один $y\in Y$ Называется функцией ($f:X → Y$).

Пусть $M$ и $N$ — два произвольных числовых множества. Говорят, что на $M$ определена функция $f$, принимающая значения из $N$, если каждому элементу $x\in X$ поставлен в соответствие один и только один элемент из $N$.

Следующее определение дается через понятие переменной величины. Переменной величиной называется величина, которая в данном исследовании принимает различные числовые значения.

Пусть $M$ — множество значений переменной величины $x$. Тогда, сели каждому значению $x\in M$ соответствует одно определенное значение другой переменной величины $y$ есть функция величины $x$, определенной на множестве $M$.

Далее рассмотрим теоретико-множественные определения.

Пусть $X$ и $Y$ — некоторые числовые множества. Функцией называется множество $f$ упорядоченных пар чисел $(x,\ y)$ таких, что $x\in X$, $y\in Y$ и каждое $x$ входит в одну и только одну пару этого множества, а каждое $y$ входит, по крайней мере, в одну пару [15].

Всякое множество $f=\<\left(x,\ y\right)\>$ упорядоченных пар $\left(x,\ y\right)$ таких, что для любых пар $\left(x’,\ y’\right)\in f$ и $\left(x»,\ y»\right)\in f$ из условия $y’≠ y»$ следует, что $x’≠x»$ называется функцией или отображением [7].

Готовые работы на аналогичную тему

Функция $f:X → Y$ — это множество $f$ упорядоченных пар $\left(x,\ y\right)\in X\times Y$, таких, что для любого элемента $x\in X$ существует единственный элемент $y\in Y$ такой, что $\left(x,\ y\right)\in f$, то есть функция — кортеж объектов $\left(f,\ X,\ Y\right)$.

В этих определениях

$x$ — независимая переменная.

$y$ — зависимая переменная.

Все возможные значения переменной $x$ называется областью определения функции, а все возможные значения переменной $y$ называется областью значения функции.

Далее будем рассматривать три способа для задания функций: аналитический, табличный и графический.

Аналитический способ задания функции

Для этого способа нам понадобится понятие аналитического выражения.

Аналитическим выражением называется произведение всех возможных математических операций над какими-либо числами и переменными.

Аналитическим способом задания функции и является её задание с помощью аналитического выражения.

Приведем далее преимущества и недостатки данного способа:

Плюсы:

1. С помощью формул мы можем определить значение функции для любого определенного значения переменной $x$;
2. Функции, заданные таким способом можно изучать с помощью аппарата математического анализа.

Минусы:

1. Малая наглядность.
2. Иногда приходится производить очень громоздкие вычисления.

Табличный способ задания функции

Данный способ задания состоит в том, что для нескольких значений независимой переменной выписываются значения зависимой переменной. Все это вносится в таблицу.

Плюс: Для любого значения независимой переменной $x$, которая внесена в таблицу, сразу узнается соответствующее значение функции $y$.

Минусы:

1. Чаще всего, нет полного задания функции;
2. Малая наглядность.

Графический способ задания функции

Введем понятие графика функции:

Графиком функции $f(x)$ называется множество точек координатной плоскости, которые имеют вид $(x,\ f\left(x\right))$.

Задание графика с помощью такого изображения его в декартовой системе координат называется графическим способом.

Пример задачи

Дан аналитический вид функции $y=x^2$. Привести табличный и графический способы задания этой же функции.

Решение.

Сначала приведем табличный способ. Так как при возведении в четную степень любого числа получим неотрицательное значение, то получим следующую таблицу:

Это и есть табличное задание.

Перейдем теперь к заданию в виде графика. Для этого отметим в декартовой системе координат точки из таблицы выше. Получим:

Источник