Функции способы задания функции графики элементарных функций

Функция. Способы задания функций.

Функция является заданной, иначе говоря, известной, если для каждого значения возможного числа аргументов можно узнать соответствующее значение функции. Наиболее распространенные три способа задания функции: табличный, графический, аналитический, существуют еще словесный и рекурсивный способы.

1. Табличный способ наиболее широко распространен (таблицы логарифмов, квадратных корней), основное его достоинство – возможность получения числового значения функции, недостатки заключаются в том, что таблица может быть трудно читаема и иногда не содержит промежуточных значений аргумента.

Аргумент х принимает заданные в таблице значения, а у определяется соответственно этому аргументу х.

2. Графический способ заключается в проведении линии (графика), у которой абсциссы изображают значения аргумента, а ординаты – соответствующие значения функции. Часто для наглядности масштабы на осях принимают разными.

Например: для нахождения по графику у, которому соответствует х = 2,5 необходимо провести перпендикуляр к оси х на отметке 2,5. Отметку можно довольно точно сделать с помощью линейки. Тогда найдем, что при х = 2,5 у равно 7,5, однако если нам необходимо найти значение у при х равном 2,76, то графический способ задания функции не будет достаточно точным, т.к. линейка не дает возможности для столь точного замера.

Достоинства этого способа задания функций заключаются в легкости и целостности восприятия, в непрерывности изменения аргумента; недостатком является уменьшение степени точности и сложность получения точных значений.

3. Аналитический способ состоит в задании функции одной или несколькими формулами. Основным достоинством этого способа является высокая точность определения функции от интересующего аргумента, а недостатком является затрата времени на проведение дополнительных математических операций.

Функцию можно задать с помощью математической формулы y=x 2 , тогда если х равно 2, то у равно 4, возводим х в квадрат.

4. Словесный способ состоит в задании функции обычным языком, т.е. словами. При этом необходимо дать входные, выходные значения и соответствие между ними.

Словесно можно задать функцию (задачу), принимающуюся в виде натурального аргумента х с соответствующим значением суммы цифр, из которых состоит значение у. Поясняем: если х равно 4, то у равно 4, а если х равно 358, то у равен сумме 3 + 5 + 8, т. е 16. Далее аналогично.

5. Рекурсивный способ состоит в задании функции через саму себя, при этом значения функции определяются через другие ее же значения. Такой способ задания функции используется в задании множеств и рядов.

При разложении числа Эйлера задается функцией:

Ее сокращение приведено ниже:

При прямом расчёте возникает бесконечная рекурсия, но можно доказать, что значение f(n) при возрастании n стремится к единице (поэтому, несмотря на бесконечность ряда, значение числа Эйлера конечно). Для приближённого вычисления значения e достаточно искусственно ограничить глубину рекурсии некоторым наперёд заданным числом и по достижении его использовать вместо f(n) единицу.

Источник

Основные элементарные функции: их свойства и графики

Основные элементарные функции, присущие им свойства и соответствующие графики – одни из азов математических знаний, схожих по степени важности с таблицей умножения. Элементарные функции являются базой, опорой для изучения всех теоретических вопросов.

Статья ниже дает ключевой материал по теме основных элементарных функций. Мы введем термины, дадим им определения; подробно изучим каждый вид элементарных функций, разберем их свойства.

Выделяют следующие виды основных элементарных функций:

• постоянная функция (константа);
• корень n -ой степени;
• степенная функция;
• показательная функция;
• логарифмическая функция;
• тригонометрические функции;
• братные тригонометрические функции.

Постоянная функция

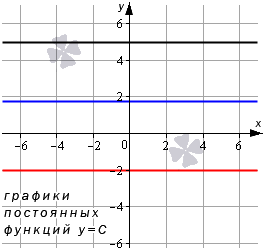
Постоянная функция определяется формулой: y = C ( C – некое действительное число) и имеет также название: константа. Данная функция определяет соответствие любому действительному значению независимой переменной x одного и того же значения переменной y – значение C .

График константы – это прямая, которая параллельна оси абсцисс и проходит через точку, имеющую координаты ( 0 , С ) . Для наглядности приведем графики постоянных функций y = 5 , y = — 2 , y = 3 , y = 3 (на чертеже обозначено черным, красным и синим цветами соответственно).

Свойства постоянных функций:

• область определения – все множество действительных чисел;
• постоянная функция – четная;
• область значений – множество, составленное из единственного числа C ;
• постоянная функция является невозрастающей и неубывающей;
• постоянная функция – прямая линия, о выпуклости или вогнутости здесь речи быть не может;
• асимптоты отсутствуют;
• точка прохождения функции на координатной плоскости – ( 0 ; С ) .

Корень n-й степени

Данная элементарная функция определяется формулой y = x n ( n – натуральное число больше единицы).

Рассмотрим две вариации функции.

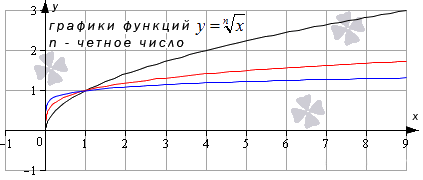
1. Корень n -й степени, n – четное число

Для наглядности укажем чертеж , на котором изображены графики таких функций: y = x , y = x 4 и y = x 8 . Эти функции отмечены цветом: черный, красный и синий соответственно.

Похожий вид у графиков функции четной степени при иных значениях показателя.

Свойства функции корень n-ой степени, n – четное число

• область определения – множество всех неотрицательных действительных чисел [ 0 , + ∞ ) ;
• когда x = 0 , функция y = x n имеет значение, равное нулю;
• данная функция- функция общего вида (не является ни четной, ни нечетной);
• область значений: [ 0 , + ∞ ) ;
• данная функция y = x n при четных показателях корня возрастает на всей области определения;
• функция обладает выпуклостью с направлением вверх на всей области определения;
• отсутствуют точки перегиба;
• асимптоты отсутствуют;
• график функции при четных n проходит через точки ( 0 ; 0 ) и ( 1 ; 1 ) .

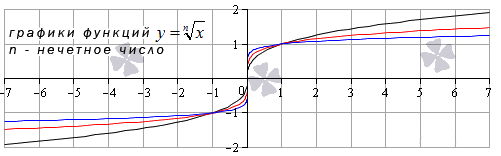
1. Корень n -й степени, n – нечетное число

Такая функция определена на всем множестве действительных чисел. Для наглядности рассмотрим графики функций y = x 3 , y = x 5 и x 9 . На чертеже они обозначены цветами: черный, красный и синий цвета кривых соответственно.

Иные нечетные значения показателя корня функции y = x n дадут график аналогичного вида.

Свойства функции корень n-ой степени, n – нечетное число

• область определения – множество всех действительных чисел;
• данная функция – нечетная;
• область значений – множество всех действительных чисел;
• функция y = x n при нечетных показателях корня возрастает на всей области определения;
• функция имеет вогнутость на промежутке ( — ∞ ; 0 ] и выпуклость на промежутке [ 0 , + ∞ ) ;
• точка перегиба имеет координаты ( 0 ; 0 ) ;
• асимптоты отсутствуют;
• график функции при нечетных n проходит через точки ( — 1 ; — 1 ) , ( 0 ; 0 ) и ( 1 ; 1 ) .

Степенная функция

Степенная функция определяется формулой y = x a .

Вид графиков и свойства функции зависят от значения показателя степени.

• когда степенная функция имеет целый показатель a , то вид графика степенной функции и ее свойства зависят от того, четный или нечетный показатель степени, а также того, какой знак имеет показатель степени. Рассмотрим все эти частные случаи подробнее ниже;
• показатель степени может быть дробным или иррациональным – в зависимости от этого также варьируется вид графиков и свойства функции. Мы разберем частные случаи, задав несколько условий: 0 a 1 ; a > 1 ; — 1 a 0 и a — 1 ;
• степенная функция может иметь нулевой показатель, этот случай также ниже разберем подробнее.

Степенная функция при нечетном положительном показателе

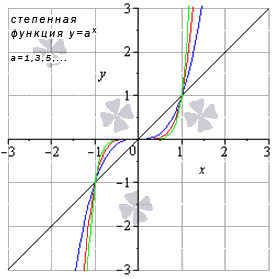
Разберем степенную функцию y = x a , когда a – нечетное положительное число, например, a = 1 , 3 , 5 …

Для наглядности укажем графики таких степенных функций: y = x (черный цвет графика), y = x 3 (синий цвет графика), y = x 5 (красный цвет графика), y = x 7 (зеленый цвет графика). Когда a = 1 , получаем линейную функцию y = x .

Свойства степенной функции, когда показатель степени – нечетный положительный

• область определения: x ∈ — ∞ ; + ∞ ;
• область значений: y ∈ — ∞ ; + ∞ ;
• функция является нечетной, поскольку y ( — x ) = — y ( x ) ;
• функция является возрастающей при x ∈ ( — ∞ ; + ∞ ) ;
• функция имеет выпуклость при x ∈ ( — ∞ ; 0 ] и вогнутость при x ∈ [ 0 ; + ∞ ) (исключая линейную функцию);
• точка перегиба имеет координаты ( 0 ; 0 ) (исключая линейную функцию);
• асимптоты отсутствуют;
• точки прохождения функции: ( — 1 ; — 1 ) , ( 0 ; 0 ) , ( 1 ; 1 ) .

Степенная функция при четном положительном показателе

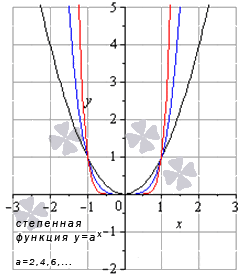
Разберем степенную функцию y = x a , когда a – четное положительное число, например, a = 2 , 4 , 6 …

Для наглядности укажем графики таких степенных функций: y = x 2 (черный цвет графика), y = x 4 (синий цвет графика), y = x 8 (красный цвет графика). Когда a = 2 , получаем квадратичную функцию, график которой – квадратичная парабола.

Свойства степенной функции, когда показатель степени – четный положительный:

• область определения: x ∈ ( — ∞ ; + ∞ ) ;
• область значений: y ∈ [ 0 ; + ∞ ) ;
• функция является четной, поскольку y ( — x ) = y ( x ) ;
• функция является возрастающей при x ∈ [ 0 ; + ∞ ) ; убывающей при x ∈ ( — ∞ ; 0 ] ;
• функция имеет вогнутость при x ∈ ( — ∞ ; + ∞ ) ;
• очки перегиба отсутствуют;
• асимптоты отсутствуют;
• точки прохождения функции: ( — 1 ; 1 ) , ( 0 ; 0 ) , ( 1 ; 1 ) .

Степенная функция при нечетном отрицательном показателе

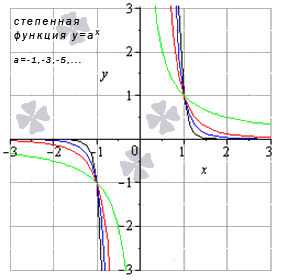
На рисунке ниже приведены примеры графиков степенной функции y = x a , когда a – нечетное отрицательное число: y = x — 9 (черный цвет графика); y = x — 5 (синий цвет графика); y = x — 3 (красный цвет графика); y = x — 1 (зеленый цвет графика). Когда a = — 1 , получаем обратную пропорциональность, график которой – гипербола.

Свойства степенной функции, когда показатель степени – нечетный отрицательный:

• область определения: x ∈ ( — ∞ ; 0 ) ∪ ( 0 ; + ∞ ) ;

Когда х = 0 , получаем разрыв второго рода, поскольку lim x → 0 — 0 x a = — ∞ , lim x → 0 + 0 x a = + ∞ при a = — 1 , — 3 , — 5 , … . Таким образом, прямая х = 0 – вертикальная асимптота;

• область значений: y ∈ ( — ∞ ; 0 ) ∪ ( 0 ; + ∞ ) ;
• функция является нечетной, поскольку y ( — x ) = — y ( x ) ;
• функция является убывающей при x ∈ — ∞ ; 0 ∪ ( 0 ; + ∞ ) ;
• функция имеет выпуклость при x ∈ ( — ∞ ; 0 ) и вогнутость при x ∈ ( 0 ; + ∞ ) ;
• точки перегиба отсутствуют;
• горизонтальная асимптота – прямая y = 0 , поскольку:

k = lim x → ∞ x a x = 0 , b = lim x → ∞ ( x a — k x ) = 0 ⇒ y = k x + b = 0 , когда а = — 1 , — 3 , — 5 , . . . .

• точки прохождения функции: ( — 1 ; — 1 ) , ( 1 ; 1 ) .

Степенная функция при четном отрицательном показателе степени

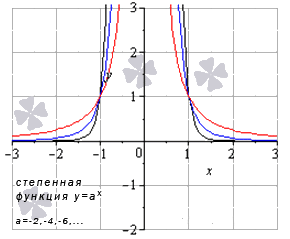
На рисунке ниже приведены примеры графиков степенной функции y = x a , когда a – четное отрицательное число: y = x — 8 (черный цвет графика); y = x — 4 (синий цвет графика); y = x — 2 (красный цвет графика).

Свойства степенной функции, когда показатель степени – четный отрицательный:

• область определения: x ∈ ( — ∞ ; 0 ) ∪ ( 0 ; + ∞ ) ;

Когда х = 0 , получаем разрыв второго рода, поскольку lim x → 0 — 0 x a = + ∞ , lim x → 0 + 0 x a = + ∞ при a = — 2 , — 4 , — 6 , … . Таким образом, прямая х = 0 – вертикальная асимптота;

• область значений: y ∈ ( 0 ; + ∞ ) ;
• функция является четной, поскольку y ( — x ) = y ( x ) ;
• функция является возрастающей при x ∈ ( — ∞ ; 0 ) и убывающей при x ∈ 0 ; + ∞ ;
• функция имеет вогнутость при x ∈ ( — ∞ ; 0 ) ∪ ( 0 ; + ∞ ) ;
• точки перегиба отсутствуют;
• горизонтальная асимптота – прямая y = 0 , поскольку:

k = lim x → ∞ x a x = 0 , b = lim x → ∞ ( x a — k x ) = 0 ⇒ y = k x + b = 0 , когда a = — 2 , — 4 , — 6 , . . . .

• точки прохождения функции: ( — 1 ; 1 ) , ( 1 ; 1 ) .

Степенная функция при рациональном или иррациональном показателе (значение больше нуля и меньше единицы)

С самого начала обратите внимание на следующий аспект: в случае, когда a – положительная дробь с нечетным знаменателем, некоторые авторы принимают за область определения этой степенной функции интервал — ∞ ; + ∞ , оговаривая при этом, что показатель a – несократимая дробь. На данный момент авторы многих учебных изданий по алгебре и началам анализа НЕ ОПРЕДЕЛЯЮТ степенные функции, где показатель – дробь с нечетным знаменателем при отрицательных значениях аргумента. Далее мы придержемся именно такой позиции: возьмем за область определения степенных функций с дробными положительными показателями степени множество [ 0 ; + ∞ ) . Рекомендация для учащихся: выяснить взгляд преподавателя на этот момент во избежание разногласий.

Итак, разберем степенную функцию y = x a , когда показатель степени – рациональное или иррациональное число при условии, что 0 a 1 .

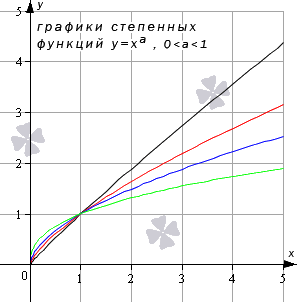
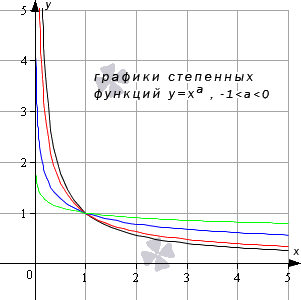
Проиллюстрируем графиками степенные функции y = x a , когда a = 11 12 (черный цвет графика); a = 5 7 (красный цвет графика); a = 1 3 (синий цвет графика); a = 2 5 (зеленый цвет графика).

Иные значения показателя степени a (при условии 0 a 1 ) дадут аналогичный вид графика.

Свойства степенной функции при 0 a 1 :

• область определения: x ∈ [ 0 ; + ∞ ) ;
• область значений: y ∈ [ 0 ; + ∞ ) ;
• данная функция – функция общего вида (не является ни нечетной, ни четной);
• функция является возрастающей при x ∈ [ 0 ; + ∞ ) ;
• функция имеет выпуклость при x ∈ ( 0 ; + ∞ ) ;
• точки перегиба отсутствуют;
• асимптоты отсутствуют;
• точки прохождения функции: ( 0 ; 0 ) , ( 1 ; 1 ) .

Степенная функция при нецелом рациональном или иррациональном показателе степени (больше единицы)

Разберем степенную функцию y = x a , когда показатель степени – нецелое рациональное или иррациональное число при условии, что a > 1 .

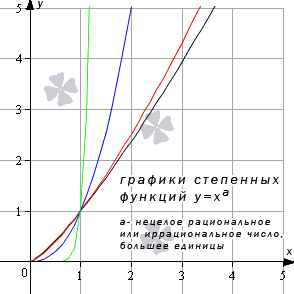
Проиллюстрируем графиками степенную функцию y = x a в заданных условиях на примере таких функций: y = x 5 4 , y = x 4 3 , y = x 7 3 , y = x 3 π (черный, красный, синий, зеленый цвет графиков соответственно).

Иные значения показателя степени а при условии a > 1 дадут похожий вид графика.

Свойства степенной функции при a > 1 :

• область определения: x ∈ [ 0 ; + ∞ ) ;
• область значений: y ∈ [ 0 ; + ∞ ) ;
• данная функция – функция общего вида (не является ни нечетной, ни четной);
• функция является возрастающей при x ∈ [ 0 ; + ∞ ) ;
• функция имеет вогнутость при x ∈ ( 0 ; + ∞ ) (когда 1 a 2 ) и выпуклость при x ∈ [ 0 ; + ∞ ) (когда a > 2 );
• точки перегиба отсутствуют;
• асимптоты отсутствуют;
• точки прохождения функции: ( 0 ; 0 ) , ( 1 ; 1 ) .

Степенная функция при действительном показателе степени (больше минус единицы и меньше нуля)

Обращаем ваше внимание! Когда a – отрицательная дробь с нечетным знаменателем, в работах некоторых авторов встречается взгляд, что область определения в данном случае – интервал — ∞ ; 0 ∪ ( 0 ; + ∞ ) с оговоркой, что показатель степени a – несократимая дробь. На данный момент авторы учебных материалов по алгебре и началам анализа НЕ ОПРЕДЕЛЯЮТ степенные функции с показателем в виде дроби с нечетным знаменателем при отрицательных значениях аргумента. Далее мы придерживаемся именно такого взгляда: возьмем за область определения степенных функций с дробными отрицательными показателями множество ( 0 ; + ∞ ) . Рекомендация для учащихся: уточните видение вашего преподавателя на этот момент во избежание разногласий.

Продолжаем тему и разбираем степенную функцию y = x a при условии: — 1 a 0 .

Приведем чертеж графиков следующий функций: y = x — 5 6 , y = x — 2 3 , y = x — 1 2 2 , y = x — 1 7 (черный, красный, синий, зеленый цвет линий соответственно).

Свойства степенной функции при — 1 a 0 :

lim x → 0 + 0 x a = + ∞ , когда — 1 a 0 , т.е. х = 0 – вертикальная асимптота;

• область значений: y ∈ 0 ; + ∞ ;
• данная функция – функция общего вида (не является ни нечетной, ни четной);
• функция является убывающей при x ∈ 0 ; + ∞ ;
• функция имеет вогнутость при x ∈ 0 ; + ∞ ;
• точки перегиба отсутствуют;
• горизонтальная асимптота – прямая y = 0 ;
• точка прохождения функции: ( 1 ; 1 ) .

Степенная функция при нецелом действительном показателе степени (меньше минус единицы)

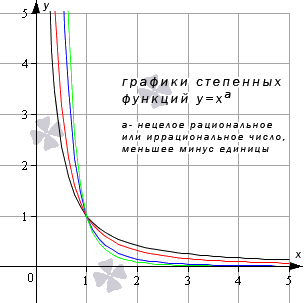
На чертеже ниже приведены графики степенных функций y = x — 5 4 , y = x — 5 3 , y = x — 6 , y = x — 24 7 (черный, красный, синий, зеленый цвета кривых соответственно).

Свойства степенной функции при a — 1 :

lim x → 0 + 0 x a = + ∞ , когда a — 1 , т.е. х = 0 – вертикальная асимптота;

• область значений: y ∈ ( 0 ; + ∞ ) ;
• данная функция – функция общего вида (не является ни нечетной, ни четной);
• функция является убывающей при x ∈ 0 ; + ∞ ;
• функция имеет вогнутость при x ∈ 0 ; + ∞ ;
• точки перегиба отсутствуют;
• горизонтальная асимптота – прямая y = 0 ;
• точка прохождения функции: ( 1 ; 1 ) .

Когда a = 0 и х ≠ 0 , получим функцию y = x 0 = 1 , определяющую прямую, из которой исключена точка ( 0 ; 1 ) (условились, что выражению 0 0 не будет придаваться никакого значения).

Показательная функция

Показательная функция имеет вид y = a x , где а > 0 и а ≠ 1 , и график этой функции выглядит различно, исходя из значения основания a . Рассмотрим частные случаи.

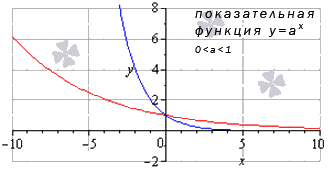
Сначала разберем ситуацию, когда основание показательной функции имеет значение от нуля до единицы ( 0 a 1 ) . Наглядным примером послужат графики функций при a = 1 2 (синий цвет кривой) и a = 5 6 (красный цвет кривой).

Подобный же вид будут иметь графики показательной функции при иных значениях основания при условии 0 a 1 .

Свойства показательной функции, когда основание меньше единицы:

• область определения – все множество действительных чисел;
• область значений: y ∈ ( 0 ; + ∞ ) ;
• данная функция – функция общего вида (не является ни нечетной, ни четной);
• показательная функция, у которой основание меньше единицы, является убывающей на всей области определения;
• функция имеет вогнутость при x ∈ — ∞ ; + ∞ ;
• точки перегиба отсутствуют;
• горизонтальная асимптота – прямая y = 0 при переменной x , стремящейся к + ∞ ;
• точка прохождения функции: ( 0 ; 1 ) .

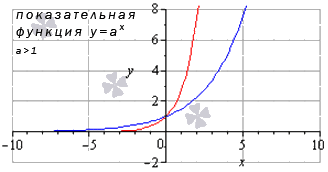
Теперь рассмотрим случай, когда основание показательной функции больше, чем единица ( а > 1 ) .

Проиллюстрируем этот частный случай графиком показательных функций y = 3 2 x (синий цвет кривой) и y = e x (красный цвет графика).

Иные значения основания, большие единицы, дадут аналогичный вид графика показательной функции.

Свойства показательной функции, когда основание больше единицы:

• область определения – все множество действительных чисел;
• область значений: y ∈ ( 0 ; + ∞ ) ;
• данная функция – функция общего вида (не является ни нечетной, ни четной);
• показательная функция, у которой основание больше единицы, является возрастающей при x ∈ — ∞ ; + ∞ ;
• функция имеет вогнутость при x ∈ — ∞ ; + ∞ ;
• точки перегиба отсутствуют;
• горизонтальная асимптота – прямая y = 0 при переменной x , стремящейся к — ∞ ;
• точка прохождения функции: ( 0 ; 1 ) .

Логарифмическая функция

Логарифмическая функция имеет вид y = log a ( x ) , где a > 0 , a ≠ 1 .

Такая функция определена только при положительных значениях аргумента: при x ∈ 0 ; + ∞ .

График логарифмической функции имеет различный вид, исходя из значения основания а.

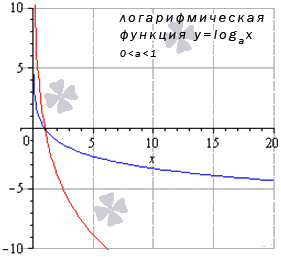
Рассмотрим сначала ситуацию, когда 0 a 1 . Продемонстрируем этот частный случай графиком логарифмической функции при a = 1 2 (синий цвет кривой) и а = 5 6 (красный цвет кривой).

Иные значения основания, не большие единицы, дадут аналогичный вид графика.

Свойства логарифмической функции, когда основание меньше единицы:

• область определения: x ∈ 0 ; + ∞ . Когда х стремится к нулю справа, значения функции стремятся к + ∞ ;
• область значений: y ∈ — ∞ ; + ∞ ;
• данная функция – функция общего вида (не является ни нечетной, ни четной);
• логарифмическая функция является убывающей на всей области определения;
• функция имеет вогнутость при x ∈ 0 ; + ∞ ;
• точки перегиба отсутствуют;
• асимптоты отсутствуют;
• точка прохождения функции: ( 1 ; 0 ) .

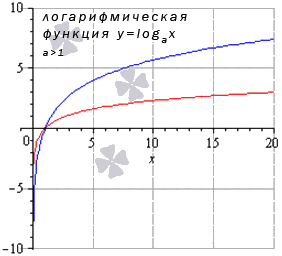
Теперь разберем частный случай, когда основание логарифмической функции больше единицы: а > 1 . На чертеже ниже – графики логарифмических функций y = log 3 2 x и y = ln x (синий и красный цвета графиков соответственно).

Иные значения основания больше единицы дадут аналогичный вид графика.

Свойства логарифмической функции, когда основание больше единицы:

• область определения: x ∈ 0 ; + ∞ . Когда х стремится к нулю справа, значения функции стремятся к — ∞ ;
• область значений: y ∈ — ∞ ; + ∞ (все множество действительных чисел);
• данная функция – функция общего вида (не является ни нечетной, ни четной);
• логарифмическая функция является возрастающей при x ∈ 0 ; + ∞ ;
• функция имеет выпуклость при x ∈ 0 ; + ∞ ;
• точки перегиба отсутствуют;
• асимптоты отсутствуют;
• точка прохождения функции: ( 1 ; 0 ) .

Тригонометрические функции, их свойства и графики

Тригонометрические функции – это синус, косинус, тангенс и котангенс. Разберем свойства каждой из них и соответствующие графики.

В общем для всех тригонометрических функций характерно свойство периодичности, т.е. когда значения функций повторяются при разных значениях аргумента, отличающихся друг от друга на величину периода f ( x + T ) = f ( x ) ( T – период). Таким образом, в списке свойств тригонометрических функций добавляется пункт «наименьший положительный период». Помимо этого, будем указывать такие значения аргумента, при которых соответствующая функция обращается в нуль.

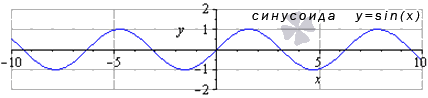
1. Функция синус: y = sin ( х )

График данной функции называется синусоида.

Свойства функции синус:

• область определения: все множество действительных чисел x ∈ — ∞ ; + ∞ ;
• наименьший положительный период: Т = 2 π ;
• функция обращается в нуль, когда x = π · k , где k ∈ Z ( Z – множество целых чисел);
• область значений: y ∈ — 1 ; 1 ;
• данная функция – нечетная, поскольку y ( — x ) = — y ( x ) ;
• функция является возрастающей при x ∈ — π 2 + 2 π · k ; π 2 + 2 π · k , k ∈ Z и убывающей при x ∈ π 2 + 2 π · k ; 3 π 2 + 2 π · k , k ∈ Z ;
• функция синус имеет локальные максимумы в точках π 2 + 2 π · k ; 1 и локальные минимумы в точках — π 2 + 2 π · k ; — 1 , k ∈ Z ;
• функция синус вогнутая, когда x ∈ — π + 2 π · k ; 2 π · k , k ∈ Z и выпуклая, когда x ∈ 2 π · k ; π + 2 π · k , k ∈ Z ;
• точки перегиба имеют координаты π · k ; 0 , k ∈ Z ;
• асимптоты отсутствуют.

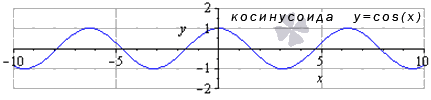
График данной функции называется косинусоида.

Свойства функции косинус:

• область определения: x ∈ — ∞ ; + ∞ ;
• наименьший положительный период: Т = 2 π ;
• функция обращается в нуль, когда x = π 2 + π · k при k ∈ Z ( Z – множество целых чисел);
• область значений: y ∈ — 1 ; 1 ;
• данная функция – четная, поскольку y ( — x ) = y ( x ) ;
• функция является возрастающей при x ∈ — π + 2 π · k ; 2 π · k , k ∈ Z и убывающей при x ∈ 2 π · k ; π + 2 π · k , k ∈ Z ;
• функция косинус имеет локальные максимумы в точках 2 π · k ; 1 , k ∈ Z и локальные минимумы в точках π + 2 π · k ; — 1 , k ∈ z ;
• функция косинус вогнутая, когда x ∈ π 2 + 2 π · k ; 3 π 2 + 2 π · k , k ∈ Z и выпуклая, когда x ∈ — π 2 + 2 π · k ; π 2 + 2 π · k , k ∈ Z ;
• точки перегиба имеют координаты π 2 + π · k ; 0 , k ∈ Z
• асимптоты отсутствуют.

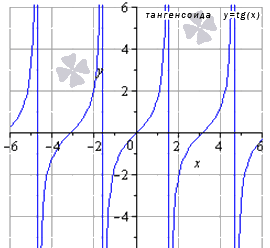
График данной функции называется тангенсоида.

Свойства функции тангенс:

• область определения: x ∈ — π 2 + π · k ; π 2 + π · k , где k ∈ Z ( Z – множество целых чисел);
• Поведение функции тангенс на границе области определения lim x → π 2 + π · k + 0 t g ( x ) = — ∞ , lim x → π 2 + π · k — 0 t g ( x ) = + ∞ . Таким образом, прямые x = π 2 + π · k k ∈ Z – вертикальные асимптоты;
• наименьший положительный период: Т = π ;
• функция обращается в нуль, когда x = π · k при k ∈ Z ( Z – множество целых чисел);
• область значений: y ∈ — ∞ ; + ∞ ;
• данная функция – нечетная, поскольку y ( — x ) = — y ( x ) ;
• функция является возрастающей при — π 2 + π · k ; π 2 + π · k , k ∈ Z ;
• функция тангенс является вогнутой при x ∈ [ π · k ; π 2 + π · k ) , k ∈ Z и выпуклой при x ∈ ( — π 2 + π · k ; π · k ] , k ∈ Z ;
• точки перегиба имеют координаты π · k ; 0 , k ∈ Z ;
• наклонные и горизонтальные асимптоты отсутствуют.

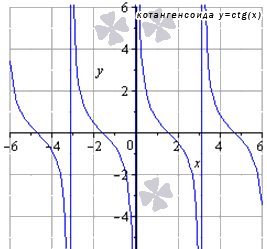
График данной функции называется котангенсоида.

Свойства функции котангенс:

• область определения: x ∈ ( π · k ; π + π · k ) , где k ∈ Z ( Z – множество целых чисел);

Поведение функции котангенс на границе области определения lim x → π · k + 0 t g ( x ) = + ∞ , lim x → π · k — 0 t g ( x ) = — ∞ . Таким образом, прямые x = π · k k ∈ Z – вертикальные асимптоты;

• наименьший положительный период: Т = π ;
• функция обращается в нуль, когда x = π 2 + π · k при k ∈ Z ( Z – множество целых чисел);
• область значений: y ∈ — ∞ ; + ∞ ;
• данная функция – нечетная, поскольку y ( — x ) = — y ( x ) ;
• функция является убывающей при x ∈ π · k ; π + π · k , k ∈ Z ;
• функция котангенс является вогнутой при x ∈ ( π · k ; π 2 + π · k ] , k ∈ Z и выпуклой при x ∈ [ — π 2 + π · k ; π · k ) , k ∈ Z ;
• точки перегиба имеют координаты π 2 + π · k ; 0 , k ∈ Z ;
• наклонные и горизонтальные асимптоты отсутствуют.

Обратные тригонометрические функции, их свойства и графики

Обратные тригонометрические функции – это арксинус, арккосинус, арктангенс и арккотангенс. Зачастую, в связи с наличием приставки «арк» в названии, обратные тригонометрические функции называют аркфункциями.

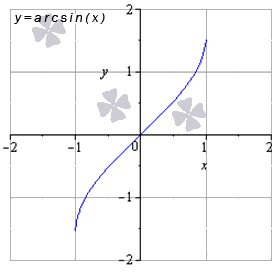
1. Функция арксинус: y = a r c sin ( х )

Свойства функции арксинус:

• область определения: x ∈ — 1 ; 1 ;
• область значений: y ∈ — π 2 ; π 2 ;
• данная функция – нечетная, поскольку y ( — x ) = — y ( x ) ;
• функция является возрастающей на всей области определения;
• функция арксинус имеет вогнутость при x ∈ 0 ; 1 и выпуклость при x ∈ — 1 ; 0 ;
• точки перегиба имеют координаты ( 0 ; 0 ) , она же – нуль функции;
• асимптоты отсутствуют.

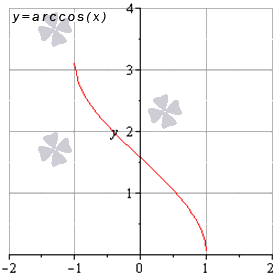
1. Функция арккосинус: y = a r c cos ( х )

Свойства функции арккосинус:

• область определения: x ∈ — 1 ; 1 ;
• область значений: y ∈ 0 ; π ;
• данная функция — общего вида (ни четная, ни нечетная);
• функция является убывающей на всей области определения;
• функция арккосинус имеет вогнутость при x ∈ — 1 ; 0 и выпуклость при x ∈ 0 ; 1 ;
• точки перегиба имеют координаты 0 ; π 2 ;
• асимптоты отсутствуют.

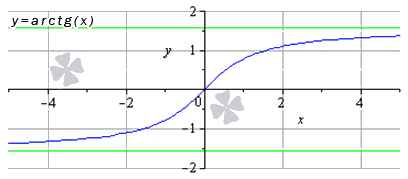
1. Функция арктангенс: y = a r c t g ( х )

Свойства функции арктангенс:

• область определения: x ∈ — ∞ ; + ∞ ;
• область значений: y ∈ — π 2 ; π 2 ;
• данная функция – нечетная, поскольку y ( — x ) = — y ( x ) ;
• функция является возрастающей на всей области определения;
• функция арктангенс имеет вогнутость при x ∈ ( — ∞ ; 0 ] и выпуклость при x ∈ [ 0 ; + ∞ ) ;
• точка перегиба имеет координаты ( 0 ; 0 ) , она же – нуль функции;
• горизонтальные асимптоты – прямые y = — π 2 при x → — ∞ и y = π 2 при x → + ∞ (на рисунке асимптоты – это линии зеленого цвета).

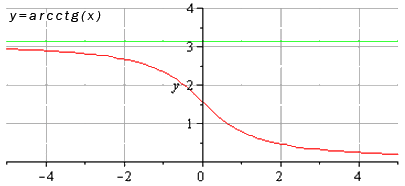
1. Функция арккотангенс: y = a r c c t g ( х )

Свойства функции арккотангенс:

• область определения: x ∈ — ∞ ; + ∞ ;
• область значений: y ∈ ( 0 ; π ) ;
• данная функция – общего вида;
• функция является убывающей на всей области определения;
• функция арккотангенс имеет вогнутость при x ∈ [ 0 ; + ∞ ) и выпуклость при x ∈ ( — ∞ ; 0 ] ;
• точка перегиба имеет координаты 0 ; π 2 ;
• горизонтальные асимптоты – прямые y = π при x → — ∞ (на чертеже – линия зеленого цвета) и y = 0 при x → + ∞ .

Источник