- Функции. Область определения и множество значений; график функции, построение графиков функции, заданных различными способами. Свойства функции. план-конспект занятия по алгебре (10, 11 класс)
- Скачать:
- Предварительный просмотр:
- Функция. Область определения и область значений функции. Графики функции
- Содержание
- Графики элементарных функций
- Линейная функция
- Обратная пропорциональность
- Степенная функция
- Показательная функция
- Логарифмическая функция
- Тригонометрическая функция
- Обратные тригонометрические функции
Функции. Область определения и множество значений; график функции, построение графиков функции, заданных различными способами. Свойства функции.
план-конспект занятия по алгебре (10, 11 класс)
Функции. Область определения и множество значений; график функции, построение графиков функции, заданных различными способами. Свойства функции.
Скачать:
| Вложение | Размер |
|---|---|
| 80_funktsii_oblast_opredeleniya_i_mnozhestvo_znacheniy.doc | 136 КБ |
Предварительный просмотр:
Тема: Функции. Область определения и множество значений; график функции, построение графиков функции, заданных различными способами. Свойства функции.
- дать определение понятий «функция», «область определения», «область значений», «график функции»;
- рассмотреть способы задания функций;
- рассмотреть свойства функций (нули функций, промежутки знакопостоянства, промежутки возрастания и убывания функции, четность и нечетность функции)
- рассмотреть свойства некоторых элементарных функций
Функция — одно из важнейших математических понятий. Функцией называют такую зависимость переменной у от переменной х, при которой каждому значению переменной х соответствует единственное значение переменной у.
Переменную х называют независимой переменной или аргументом. Переменную у называют зависимой переменной. Говорят также, что переменная у является функцией от переменной х. Значения зависимой переменной называют значениями функции.
Если зависимость переменной у от переменной х является функцией, то коротко это записывают так: y=f(x ). (Читают: у равно f от х .) Символом f(x) обозначают значение функции, соответствующее значению аргумента, равному х .
Все значения независимой переменной образуют область определения функции . Все значения, которые принимает зависимая переменная, образуют область значений функции .
Если функция задана формулой и ее область определения не указана, то считают, что область определения функции состоит из всех значений аргумента, при которых формула имеет смысл.
Способы задания функции:
1. аналитический способ (функция задается с помощью математической формулы;
2. табличный способ (функция задается с помощью таблицы)
3. описательный способ (функция задается словесным описанием)
4. графический способ (функция задается с помощью графика).
Графиком функции называют множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты — соответствующим значениям функции.
ОСНОВНЫЕ СВОЙСТВА ФУНКЦИЙ
Нуль функции – такое значение аргумента, при котором значение функции равно нулю .
2. Промежутки знакопостоянства функции
Промежутки знакопостоянства функции – такие множества значений аргумента, на которых значения функции только положительны или только отрицательны.
3. Возрастание (убывание) функции.
Возрастающая в некотором промежутке функция — функция, у которой большему значению аргумента из этого промежутка соответствует большее значение функции.
Функция у = f (x) называется возрастающей на интервале (а; b), если для любых x 1 и x 2 из этого интервала таких, что x 1 2 , справедливо неравенство f(x 1 ) 2 ).
Убывающая в некотором промежутке функция — функция, у которой большему значению аргумента из этого промежутка соответствует меньшее значение функции.
Функция у = f (x) называется убывающей на интервале (а; b) , если для любых x 1 и x 2 из этого интервала таких, что x 1 2 , справедливо неравенство f(x 1 )>f(x 2 ).
4. Четность (нечетность) функции
Четная функция — функция, у которой область определения симметрична относительно начала координат и для любого х из области определения выполняется равенство f(-x) = f(x) . График четной функции симметричен относительно оси ординат.
Например, у = х 2 — четная функция.
Нечетная функция — функция, у которой область определения симметрична относительно начала координат и для любого х из области определения справедливо равенство f(-x) = — f(x). График нечетной функции симметричен относительно начала координат.
Например: у = х 3 — нечетная функция .
Функция общего вида не является четной или нечетной ( у = х 2 +х ).
Свойства некоторых функций и их графики
1. Линейной функцией называется функция вида , где k и b – числа.
Область определения линейной функции – множество R действительных чисел.
Графиком линейной функции у = kx + b (k ≠ 0) является прямая проходящая через точку (0; b ) и параллельная прямой у = kx.
Прямая, не параллельная оси Оу, является графиком линейной функции.
Свойства линейной функции.
1. При k > 0 функция у = kx + b возрастающая в области определения.
2. При k 0 функция у = kx + b убывающая в области определения.
3. Множеством значений функции y = kx + b(k ≠ 0 ) является вся числовая прямая, т.е. множество R действительных чисел.
При k = 0 множество значений функции у = kx + b состоит из одного числа b.
3. При b = 0 и k = 0 функция не является ни четной, ни нечетной.
При k = 0 линейная функция имеет вид у = b и при b ≠ 0 она является четной.
При k = 0 и b = 0 линейная функция имеет вид у = 0 и являете одновременно четной и нечетной.
Графиком линейной функции у = b является прямая, проходящая через точку (0; b ) и параллельная оси Ох. Заметим, что при b = 0 график функции у = b совпадаете осью Ох .
5. При k > 0 имеем, что у > 0, если и у 0, если . При k 0 имеем, что у > 0, если и у
2. Функция y = x 2
Область определения этой функции — множество R действительных чисел.
Придавая переменной х несколько значений из области определения функции и вычисляя соответствующие значения у по формуле y = x 2 , изображаем график функции.
График функции y = x 2 называется параболой.
Свойства функции у = х 2 .
1. Если х = 0, то у = 0, т.е. парабола имеет с осями координат общую точку (0; 0) — начало координат.
2. Если х ≠ 0 , то у > 0, т.е. все точки параболы, кроме начала координат, лежат над осью абсцисс.
3. Множеством значений функции у = х 2 является промежуток [0; + ∞).
4. Если значения аргумента отличаются только знаком, то значения функции равны, т.е. парабола симметрична относительно оси ординат (функция у = х 2 — четная).
5. На промежутке [0; + ∞) функция у = х 2 возрастает.
6. На промежутке (-∞; 0] функция у = х 2 убывает.
7. Наименьшее значение функция принимает в точке х = 0, оно равно 0. Наибольшего значения не существует.
Область определения этой функции — промежуток [0;+∞), т. е. все неотрицательные числа.
Придавая переменной х несколько значений из области определения функции и вычисляя соответствующие значения у по формуле , изображаем график функции.
1. Если х = 0, то у = 0, т.е. график функции имеет с осями координат общую точку (0; 0) — начало координат.
2. Если х > 0, то у > 0, т.е. все точки графика функции, кроме начала координат, лежат над осью абсцисс.
3. Множеством значений функции является промежуток [0;+∞) .
4. Функция не является ни четной, ни нечетной.
5. Функция возрастающая в области определения.
6. Наименьшее значение функция принимает в точке х = 0, оно равно 0. Наибольшего значения не существует.
4. Функция y = x 3
Область определения этой функции — множество R действительных чисел,
Придавая переменной х несколько значений из области определения функции и вычисляя соответствующие значения у по формуле у = х 3 , изображаем график функции.
График функции у= х 3 называется кубической параболой.
Свойства функции y = x 3 .
1. Если х = 0, то у = 0, т.е. кубическая парабола пересекает оси координат в точке (0; 0) — начале координат.
2. Если х > 0, то у > 0, а если х 0, то у
3. Множеством значений функции у = х 3 является вся числовая прямая.
4. Если значения аргумента отличаются только знаком, то и значения функции отличаются только знаком, т.е. кубическая парабола симметрична относительно начала координат (функция у = х 3 — нечетная).
4. Функция у = х 3 возрастающая в области определения.
Область определения этой функции — множество R действительных чисел.
Пользуясь определением модуля числа х при х > О получим у = х, а при х у = — х . Таким образом, имеем:
График функции состоит из двух частей: части прямой у = х при х ≥ 0 и из части прямой у =- х при х
1. Если х = 0, то у = 0, т.е. график пересекает оси координат в точке (0; 0) — начале координат.
2. Если х ≠ 0, то у > 0, т.е. все точки графика функции y = |x|, кроме начала координат, лежат над осью абсцисс.
3. Множеством значений функции y = |x| является промежуток [0;+∞).
4. Если значения аргумента отличаются только знаком, то значения функции равны, т.е. график функции симметричен относительно ординат (функция y = |x| — четная).
5. На промежутке [0;+∞) функция y = |x| возрастает.
6. На промежутке (-∞;0] функция y = |x| убывает.
7. Наименьшее значение функция принимает в точке х, оно равно 0. Наибольшего значения не существует.
Область определения функции: .
Область значений функции: .
2. Промежутки знакопостоянства,
Если k > 0, то у > 0 при х > 0; у х
Если k у х > 0; у > 0 при х
3. Промежутки возрастания и убывания.
Если k > 0, то функция убывает при .
4. Четность (нечетность) функции.
- Найдите область определения функции
- При каких значениях
функция принимает положительные значения?
Постройте график функции
- Постройте график функции
и укажите координаты точек пересечения этих графиков.
- Постройте график функции
Проходит ли график через точку А(-35, -65)?
- Вычислите координаты точек пересечения параболы
и прямой
- Какая из прямых у = 3х — 1, у = 2х + 4 или у = -2х проходит через начало координат? Постройте график этой функции.
Источник
Функция. Область определения и область значений функции. Графики функции
Функция y=f(x) — это такая зависимость переменной y от переменной x , когда каждому допустимому значению переменной x соответствует единственное значение переменной y .
Областью определения функции D(f) называют множество всех допустимых значений переменной x .
Область значений функции E(f) — множество всех допустимых значений переменной y .
График функции y=f(x) — множество точек плоскости, координаты которых удовлетворяют данной функциональной зависимости, то есть точек, вида M (x; f(x)) . График функции представляет собой некоторую линию на плоскости.
Содержание
Графики элементарных функций
Линейная функция
Линейная функция — это функция вида y=kx+b , где k и b некоторые действительные числа.
Если b=0 , то функция примет вид y=kx и будет называться прямой пропорциональностью.
D(f) : x \in R;\enspace E(f) : y \in R
График линейной функции — прямая.
Угловой коэффициент k прямой y=kx+b вычисляется по следующей формуле:
k= tg \alpha , где \alpha — угол наклона прямой к положительному направлению оси Ox .
1) Функция монотонно возрастает при k > 0 .
2) Функция монотонно убывает при k .
3) Если k=0 , то придавая b произвольные значения, получим семейство прямых параллельных оси Ox .
Обратная пропорциональность
Обратной пропорциональностью называется функция вида y=\frac
Графиком функции y=\frac
1) Если k > 0 , то график функции будет располагаться в первой и третьей четверти координатной плоскости.
2) Если k , то график функции будет располагаться во второй и четвертой координатной плоскости.
Степенная функция
Степенная функция — это функция вида y=x^n , где n — отличное от нуля, действительное число
1) Если n=2 , то y=x^2 . D(f) : x \in R; \: E(f) : y \in [0; +\infty) .
Графиком функции y=x^2 является парабола.
2) Если n=3 , то y=x^3 . D(f) : x \in R; \: E(f) : y \in R .
Графиком функции y=x^3 является кубическая парабола.
3) Если n=\frac<1> <2>, то y=x^\tfrac<1> <2>или y=\sqrt
4) Если n=\frac<1> <3>, то y=x^\tfrac<1> <3>или y=\sqrt[3]
Показательная функция
Показательная функция — это функция вида y=a^x , где a=const, a > 0, a \neq 1
D(f) : x \in R; \: E(f) : y \in (0; +\infty ) .
Графиком показательной функции является экспонента.
1) Функция будет монотонно возрастать при a > 1 .
2) Функция монотонно убывает при 0 .
Например: y=\left (\frac<1> <2>\right )^
Логарифмическая функция
Логарифмическая функция — это функция вида y=\log_x , где a — действительное число, a > 0, \: a \neq 1
D(f) : x \in (0; +\infty ); \: E(f) : y \in R .
1) Функция монотонно возрастает при a > 1 .
2) Функция будет монотонно убывать при 0 .
Тригонометрическая функция
К тригонометрическим функциям относят функции вида:
1) y=\sin x . D(f) : x \in R; \: E(f) : y \in [-1; 1] ; основной период функции T=2 \pi
2) y = \cos x . D(f) : x \in R; \: E(f) : y \in [-1; 1] ; основной период функции T=2 \pi
3) y = tg x . D(f) : x \in \left \< R /x \neq \frac<\pi><2>+\pi n\right \>, n \in \mathbb
4) y = ctg x . D(f) : x \in \left \< R /x \neq 0+\pi n\right \>, n \in \mathbb
Обратные тригонометрические функции
К обратным тригонометрическим функциям относят функции вида:
1) y=\arcsin x . D(f) : x \in [-1; 1], \: E(f) : y \in \left [ -\frac<\pi><2>; \frac<\pi> <2>\right ]
2) y=arccos x . D(f) : x \in [-1; 1], \: E(f) : y \in [0; \pi]
3) y=arctg x . D(f) : x \in R, \: E(f) : y \in \left (-\frac<\pi><2>; \frac<\pi> <2>\right )
4) y= arcctg x . D(f) : x \in R, \: E(f) : y \in \left (0; \pi \right )
Источник


 функция принимает положительные значения?
функция принимает положительные значения?
 и укажите координаты точек пересечения этих графиков.
и укажите координаты точек пересечения этих графиков.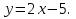
 и прямой
и прямой 























