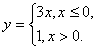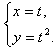Функции область определения значений способы задания свойства функции

2. Определение, способы задания и свойства функции

Определение:Если каждому элементухмножестваХпо какому-либо законуf(или по определенному правилуf) ставится в соответствие единственный элементуиз множестваУ, то говорят, что заданафункциональная зависимостьуотх по законуy=f(x)илифункция y=f(x).

При этом х называетсянезависимой переменной(илиаргументом),у – зависимой переменной(илизначением функции). МножествоХназываетсяобластью определения( илиобластью существования) функции и обозначаетсяD(f), множествоУназываетсяобластью значений функции и обозначаетсяЕ(f).

Если множество Хне оговорено, то под областью определения функции подразумевается область допустимых значений независимой переменнойх, при котом формула имеет смысл. Например, для.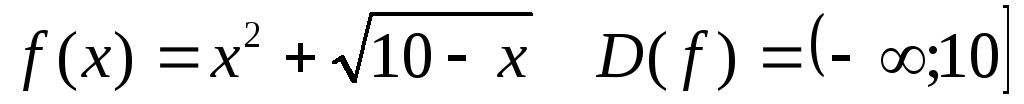

Задать функцию– значит, указать законfили правило, позволяющее, знаях.находить соответствующее значениеу.

1. Аналитический– если функция задана с помощью формулы. Наиболее удобный способ для математического анализа, позволяющий исследовать функцию.

2. Табличный– если задана таблица значений функции, соответствующих определенным значением аргумента. Этот способ имеет широкое применение в экономике: экспериментальные измерения, таблицах бухгалтерской отчетности, банковской деятельности, статистических данных и т.п.

3. Графический– если задан график. Этот способ обычно используется с употреблением самопишущих приборов (осциллографы, сейсмографы и т.п.). В экономике используются графики, характеризующие динамику экономических параметров: объема ВВП, выручки, курсы валют, курса акций и т.п.

4. Словесный– если функция описывается правилом, составления, например, функция Дирихле:f(x)=1 , если x – рационально и f(x)=0, если x— иррационально.

1. Четность и нечетность

При этом D(f)называетсясимметричнойотносительно О(0;0). График четной функции симметричен относительно Оу, а график нечетной – относительно О(0;0).

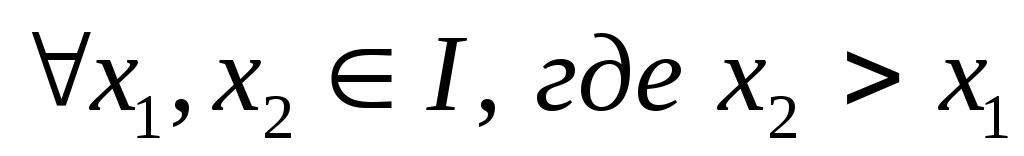
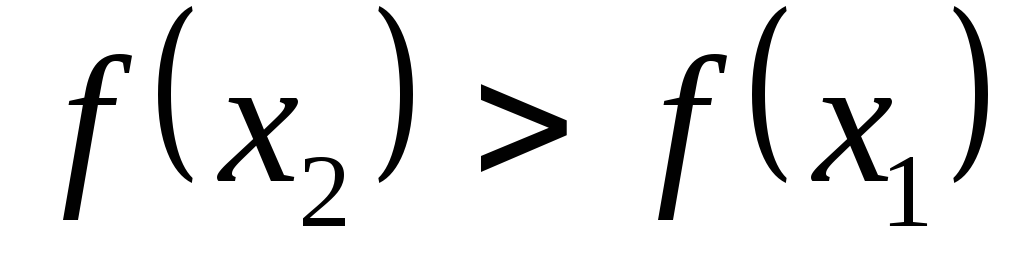
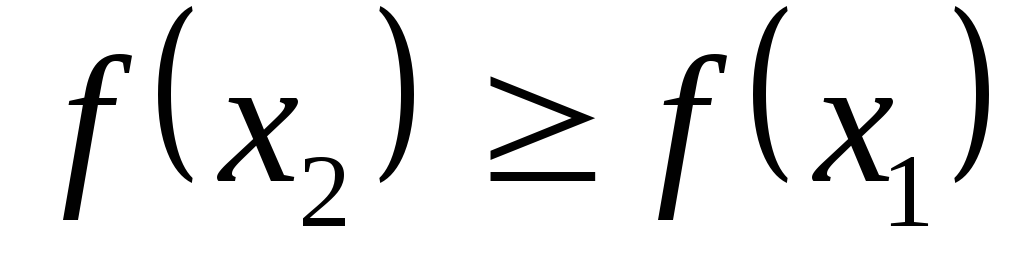
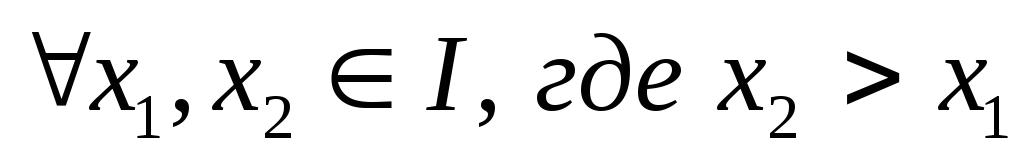
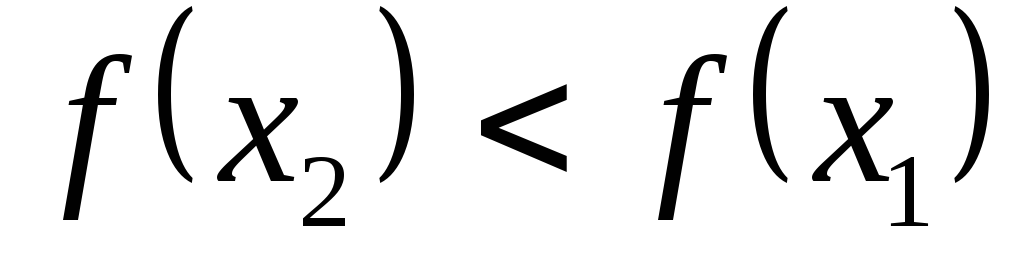
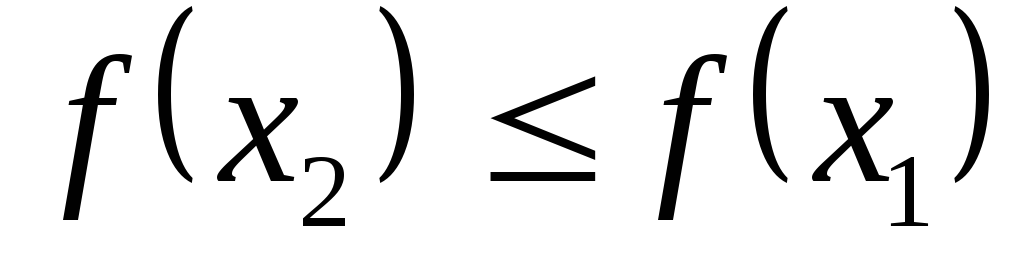
Функция называется возрастающейна промежуткеID(f), есливыполняется условие:инеубывающей, если. Функция называетсяубывающейна промежуткеID(f), есливыполняется условие:иневозрастающей, если.

Например,fубывает прих(a;b), не убывает прих(b;с)и возрастает прих(с;d)

Возрастающие, неубывающие, убывающие и невозрастающие функции на промежутке ID(f)называютсямонотоннымина этом промежутке, а возрастающие и убывающие –строго монотонными.

Функция называется ограниченнойна множествеD(f), если существует такое число М>0, чтохD(f)выполняется неравенство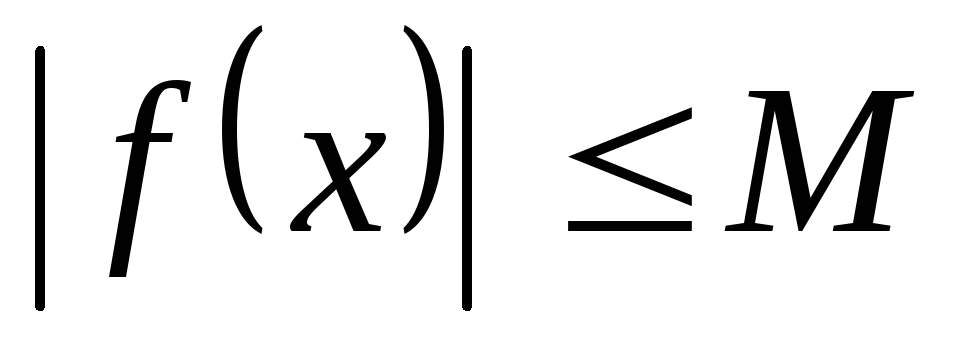. Или коротко:

если .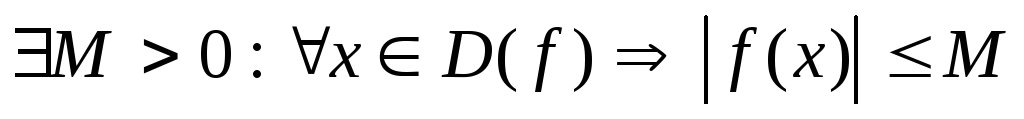

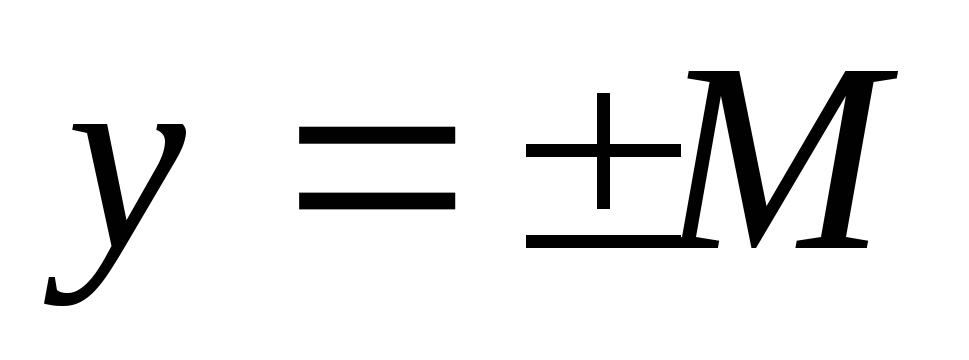
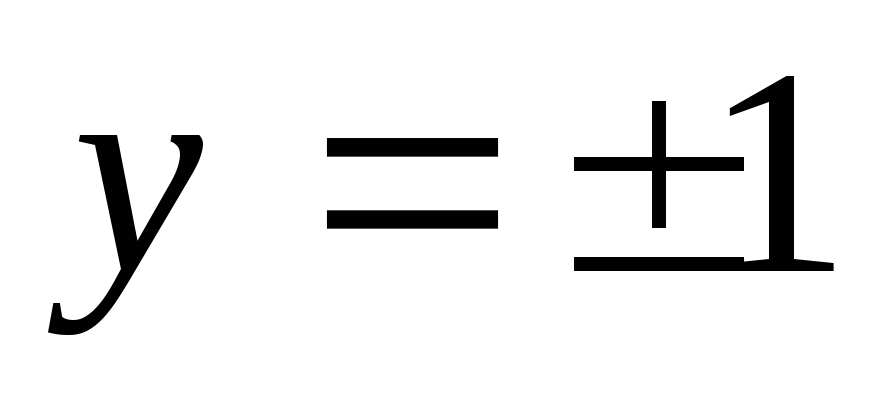
Графики таких функций ограничены прямыми . Например,у=sin x ограничена прямыми.

Число Т называется периодомфункции. Если Т – период, тоnTтакже является периодом, гдеn=±1;±2;…

Например, функция у=sin x является периодической, т.к.xD(f) sin(x+2π)=sin x. Аналогично можно доказать, что ±2π; ±4π; ±6π;… также являются периодами. Период 2π являетсянаименьшим положительными называетсяосновным.

Применение функций в экономике

Функции находят широкое применение в экономической теории и практике. Наиболее часто используются следующие функции:

1.Функция полезности (функция предпочтений) – зависимость полезности, т.е. результата, эффекта некоторого действия от уровня (интенсивности) этого действия.

2.Производственная функция зависимость результата производственной деятельности от обусловивших его факторов.

3.Функция выпуска (частный вид производственной функции) – зависимость объёма производства от наличия или потребления ресурсов.

4.Функция издержек (частный вид производственной функции) –зависимость издержек производства от объёма продукции.

5.Функция спроса, потребления и предложения – зависимость объёма спроса, потребления или предложения на отдельные товары или услуги от различных факторов (например, цены, дохода и т.п.).

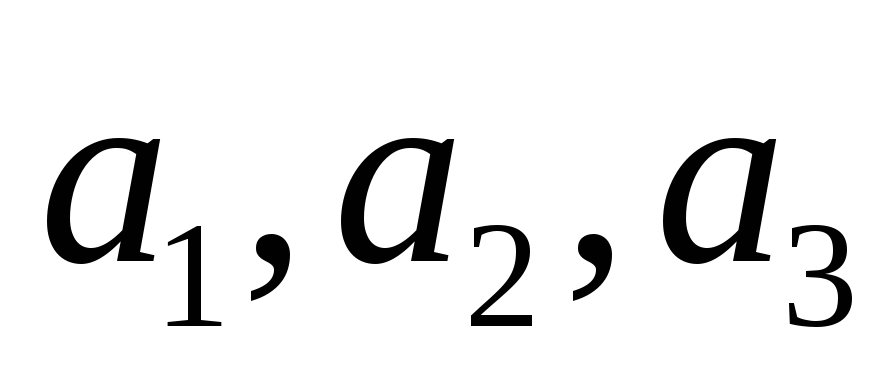
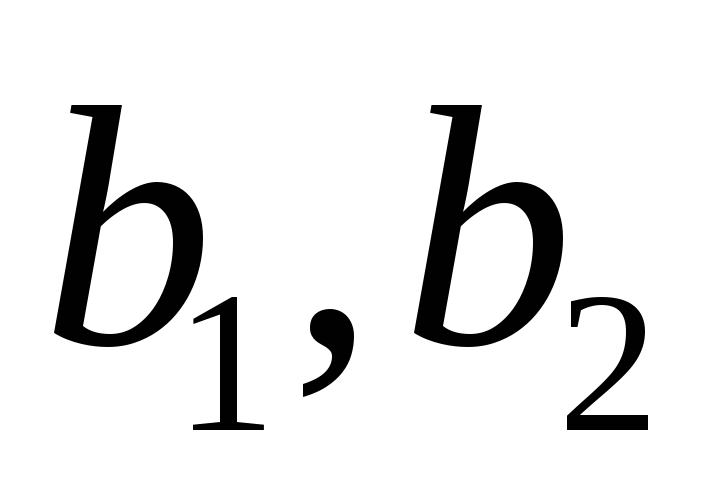
Например, исследуя зависимости спроса на различные товары от дохода можно установить уровни доходов , при которых начинается приобретение тех или иных товаров и уровни (точки) насыщениядля групп товаров первой и второй необходимости. (см. рис.1)

Рассматривая в одной системе координат кривые спроса и предложения, можно установить равновесную (рыночную) цену данного товара в процессе формирования цен в условиях конкурентного рынка (паутинообразная модель) (см. рис.2)

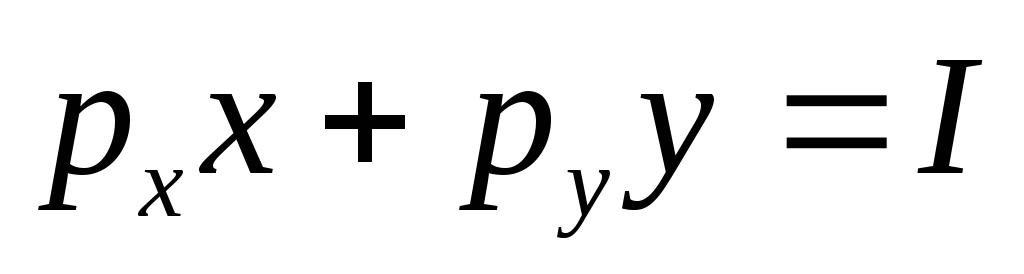
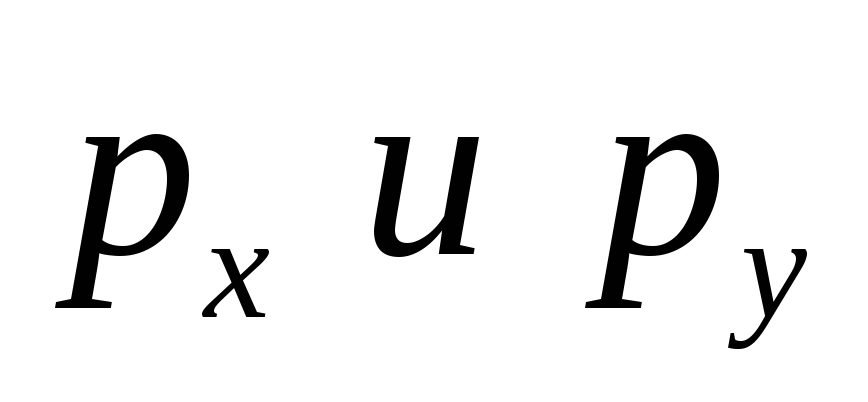
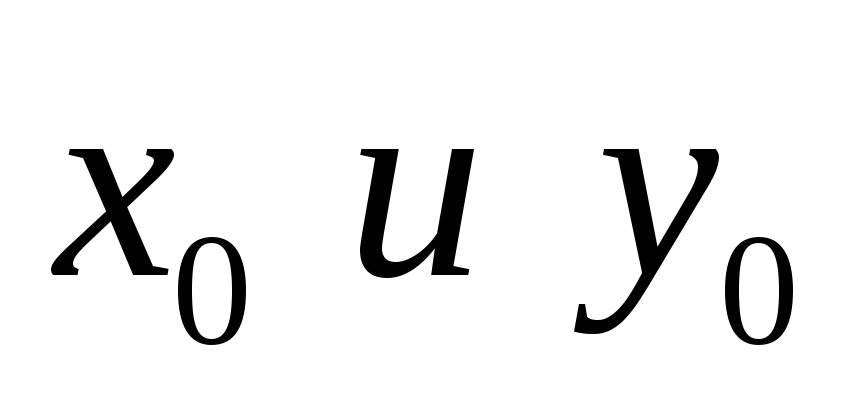
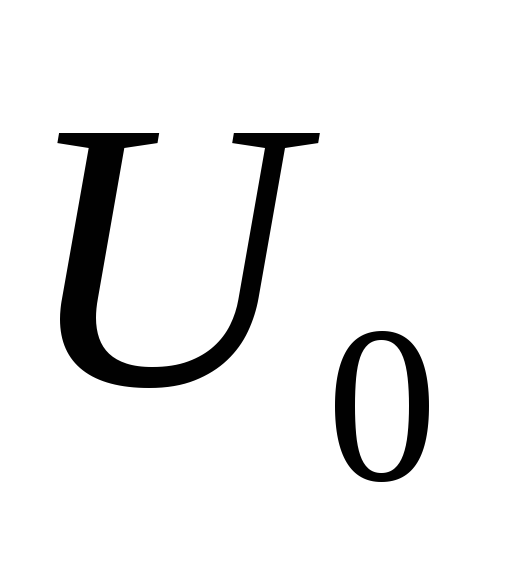
Изучая в теории потребительского спроса кривые безразличия (линии, вдоль которых полезность двух благ х и у одна и та же), например, задаваемые в виде xy=U, и линию бюджетного ограничения при ценах благ и доходе потребителяI, мы можем установить оптимальные количества благ , имеющих максимальную полезность(см. рис.3).

Товары 2-ой необходимости

Товары 1-ой необходимости

Рассматривая функции издержек (полных затрат) с(q) и дохода фирмы r(q), мы можем установить зависимость прибыли π(q)=c(q)-r(q) от объёма производства q (см. рис.4) и выявить уровни объёма производства, при которых производство продукции убыточно (0 2 / 4 2 3 4 > Следующая > >>

Тут вы можете оставить комментарий к выбранному абзацу или сообщить об ошибке.

Читайте также:  Деловое общение способы передачи

Источник

Понятие функции. Способы задания функции

Функцией называется закон, по которому числу х из заданного множества Х, поставлено в соответствие только одно число у, пишут 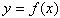, при этом x называют аргументом функции, y называют значением функции.

Существуют разные способы задания функций.

1. Аналитический способ.

Аналитический способ — это наиболее часто встречающийся способ задания функции.

Заключается он в том, что функция задается формулой, устанавливающей, какие операции нужно произвести над х, чтобы найти у. Например .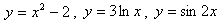

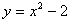
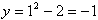
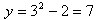
Рассмотрим первый пример — . Здесь значению x = 1 соответствует , значению x = 3 соответствует и т. д.

Функция может быть задана на разных частях множества X разными функциями.

Во всех ранее приведенных примерах аналитического способа задания, функция была задана явно. То есть, справа стояла переменная y, а слева формула от переменной х. Однако, при аналитическом способе задания, функция может быть задана и неявно.

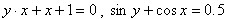
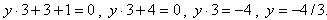
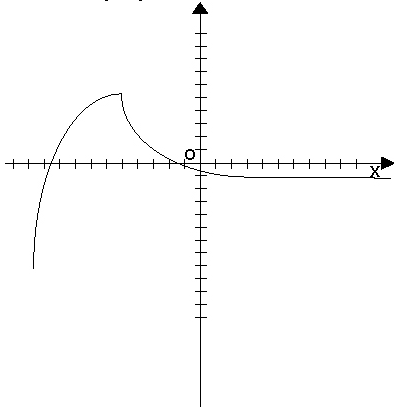
Например . Здесь, если мы задаем переменной x значение, то, чтобы найти значение переменной у (значение функции), мы должны решить уравнение. Например, для первой заданной функции при х = 3, будем решать уравнение:

. То есть, значение функции при х = 3 равно -4/3.

При аналитическом способе задания, функция может быть задана параметрически — это, когда х и у выражены через некоторый параметр t. Например,

Здесь при t = 2, x = 2, y = 4. То есть, значение функции при х = 2 равно 4.

2. Графический способ.

При графическом способе вводится прямоугольная система координат и в этой системе координат изображается множество точек с координатами (x,y). При этом 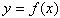. Пример:

3. Словесный способ.

Функция задается с помощью словесной формулировки. Классический пример – функция Дирихле.

«Функция равна 1, если х – рациональное число; функция равна 0, если х – иррациональное число».

4. Табличный способ.

Табличный способ наиболее удобен, когда множество Х конечно. При этом способе составляется таблица, в которой каждому элементу из множества Х, ставится в соответствие число Y.

Ошибка в тексте? Выдели её мышкой и нажми

Остались рефераты, курсовые, презентации? Поделись с нами — загрузи их здесь!

Источник

Что такое Функция?

О чем эта статья:

7 класс, 11 класс, ЕГЭ/ОГЭ

Понятие функции

Определение функции можно сформулировать по-разному. Рассмотрим несколько вариантов, чтобы усвоить наверняка.

1. Функция — это взаимосвязь между величинами, то есть зависимость одной переменной величины от другой.

Читайте также:  Способы решения алгебраических дробей

Знакомое обозначение y = f (x) как раз и выражает идею такой зависимости одной величины от другой. Величина у зависит от величины х по определенному закону, или правилу, которое обозначается f.

Вывод: меняя х (независимую переменную, или аргумент) — меняем значение у.

2. Функция — это определенное действие над переменной.

Значит, можно взять величину х, как-то над ней поколдовать — и получить соответствующую величину у.

В технической литературе можно встретить такие определения функции для устройств, в которых на вход подается х — на выходе получается у. Схематично это выглядит так:

В этом значении слово «функция» используют и в далеких от математики областях. Например, так говорят о функциях ноутбука, костей в организме или даже о функциях менеджера в компании. В каждом перечисленном случае речь идет именно о неких действиях.

3. Функция — это соответствие между двумя множествами, причем каждому элементу первого множества соответствует один элемент второго множества. Это самое популярное определение в учебниках по математике.

Например, в функции у = 2х каждому действительному числу х ставит в соответствие число в два раза большее, чем х.

Область определения — множество х, то есть область допустимых значений выражения, которое записано в формуле.

Например, для функции вида

область определения выглядит так:

• х ≠ 0 (потому что на ноль делить нельзя)

И записать это можно так: D (y): х ≠ 0.

Область значений — множество у, то есть это значения, которые может принимать функция.

Например, естественная область значений функции y = x2 — это все числа больше либо равные нулю. Можно записать вот так: Е (у): у ≥ 0.

Для примера рассмотрим соответствие между двумя множествами — человек-владелец странички в инстаграм и сама страничка, у которой есть владелец. Такое соответствие можно назвать взаимно-однозначным — у человека есть страничка, и это можно проверить. И наоборот — по аккаунту в инстаграм можно проверить, кто им владеет.

В математике тоже есть такие взаимно-однозначные функции. Например, линейная функция у = 3х +2. Каждому значению х соответствует одно и только одно значение у. И наоборот — зная у, можно сразу найти х.

Источник