- Способы задания функции двух переменных
- Лекция 1. Функции нескольких переменных
- Зміст
- Тема 1. Функции многих переменных. Основные понятия
- 1. Определение функции нескольких переменных
- 2. Предел и непрерывность функции нескольких переменных
- 3. Частные производные и дифференциалы
- Тема 2. Диференцирование сложной и неявно заданнной функции. Производные и дифференциалы высших порядков
- 4. Частные производные сложных и неявных функций. Полная производная
- 5. Частные производные второго порядка
- Тема 3. Некоторые применения частных производных
- 6. Касательная плоскость и нормаль к поверхности
- 7. Градиент
- 8. Производная по направлению
- 9. Экстремумы функции двух переменных
Способы задания функции двух переменных
ОСНОВНЫЕ ПОНЯТИЯ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ (ФНП)
ПЛАН
1. Определение функции нескольких переменных (ФНП).
2. Способы задания функции двух переменных.
3. Предел и непрерывность ФНП.
4. Частные и полное приращения функции двух переменных.
5.Частные производные первого порядка функции двух
переменных и их геометрическая интерпретация
Определение ФНП.
При изучении многих явлений приходится встречаться с функциями двух и более независимых переменных. Приведем примеры.
Пример 1. Площадь Sпрямоугольника со сторонами, длины которых равны х и у вычисляется по формуле: S = х · у, где S– является функцией двух переменных т.к. каждой паре значений х и усоответствует определенное значение площади S.
Пример 2. Объем V прямоугольного параллелепипеда с ребрами, длины которых равны х, у, z определяется по формуле V = x y z.
Здесь V – функция трех переменных x, y, z.
Определение. Функцией n переменных х1, х2,…,хn,
где (х1, х2,…,хn) ÎDÌ R n будем называть правило или
закон, по которому каждому набору переменных
(х1, х2,…,хn) ÎD ставится в соответстие единственное число
у ÎЕ Ì R. Тот факт, что задана функция n переменных
будем записывать следующим образом: у = f(х1, х2,…,хn) .
Мы будем рассматривать функции двух переменных, т.к. основные факты теории функций нескольких переменных наблюдаются уже на функции двух переменных, а также для функций двух переменных можно дать геометрическую интерпретацию.
Определение.Функцией двух переменных х, у будем называть правило
или закон, по которому каждой паре чисел (х, у) Î D
ставится в соответствие единственное число z Î Е.
Тот факт, что задана функция двух переменных, будем записывать в виде: z = f(x, у). При этом хи у будем называть независимыми переменными (аргументами), а z – зависимой переменной (функцией).
Множество D(z) называется областью определения функции. Множество Е значений, принимаемых z в области определения, называется областью изменения функции.
Функцию двух переменных z = f(х, у), где (х, у) Î D можно рассматривать как функцию точки М(х, у) координатной плоскости Оху.
Значение функции z = f(х, у) в точке М0(х0, у0) называют частным значением функциии обозначают одним из способов:
z(х0, у0), 
Способы задания функции двух переменных
Функция двух переменных, как и функция одной переменной, может быть задана разными способами.
1) Аналитический способ состоит в том, что функция zпредставлена с помощью формулы. Если при этом область определения D(z) не указана, то под ней понимают множество таких пар значений (х, у), при которых заданная формула имеет смысл. Областью определения может быть вся плоскость или её часть, ограниченная некоторыми линиями. Линию, ограничивающую область, называют границей области. Точки области, не лежащие
 |
на границе, называются внутренними. Об-
ласть, состоящая только из внутренних точек,
называется открытой, область с присоеди-
ненной к ней границей называется замкнутой
областью. Например, функция
z = ln(4 – х 2 – у 2 ) имеет областью определе-
Рис. 1 ния внутреннюю часть круга х 2 + у 2
Если поверхность является графиком функции двух переменных, то уравнение, определяющее эту функцию, является уравнением поверхности.
Например, функция 
 |
 |
Предел функции
Понятия предела функции двух (и более) переменных и непрерывности вводится аналогично понятию предела и непрерывности функции одной переменной.
вем число: 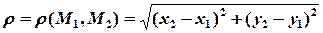
Определение.d-окрестностью точки М0(х0, у0) назовем множество всех
точек М(х, у) плоскости, таких, что r(М, М0) 0 существует d > 0 такое, что для всех
точек М(х, у) Î D(z), отличных от точки М0 и удовлетво-
ряющих неравенству r(М, М0)
Источник
Лекция 1. Функции нескольких переменных
| Сайт: | Навчальний сайт ХНАДУ |
| Курс: | Вища Математика (2 семестр) Вишневецький А.Л. |
| Книга: | Лекция 1. Функции нескольких переменных |
| Надруковано: | Гість |
| Дата: | четвер 18 листопад 2021 14:25 |
Зміст
Тема 1. Функции многих переменных. Основные понятия
1. Определение функции нескольких переменных
Если каждой паре (x, y) значений двух переменных x, y из некоторого множества D соответствует одно определенное значение переменной z, то говорят, что z – функция двух переменных x, y, определенная в области D. Множество D называется областью определения функции Z. Символически функция двух переменных записывается в виде равенства z = f(x, y), в котором f обозначает знак соответствия. Геометрически область определения D представляет собой некоторую часть плоскости Oxy, ограниченную линиями, которые могут принадлежать или не принадлежать области. Если функция задана формулой и область D её определения не указана, то считается, что D есть множество всех значений переменных, для которых эта формула имеет смысл.
Вообще, величина z называется функцией переменных x1, x2, . xn, если каждой совокупности (x1, x2, . xn) переменных x1, x2, . xn из некоторого множества D соответствует определенное значение y, что символически записывается в виде z = f(x1, x2, . xn). Множество D называется областью определения функции y.
Для каждой пары (x,y) из области определения функции z = f(x, y) можно построить точку M(x, y, z), где z = f(x, y). Множество всех таких точек называется графиком функции z = f(x, y). Обычно это некоторая поверхность.
2. Предел и непрерывность функции нескольких переменных
Окрестностью точки на плоскости называется любой круг с центром в этой точке, а окрестностью точки в пространстве – любой шар с центром в этой точке.
На функции многих переменных переносятся такие понятия, как предел, непрерывность и т.п.
Например, функция непрерывна в любой точке плоскости, за исключением начала координат. Здесь функция терпит бесконечный разрыв.
Функция, непрерывная в каждой точке некоторой области, называется непрерывной в этой области.
3. Частные производные и дифференциалы
Рассмотрим функцию z = f(x, y), определенную в точке M(x; y ) и некоторой ее окрестности. Если переменной x придать некоторое приращение Δx, а y оставить постоянной, то функция z = f(x, y) получит приращение Δxz = f(x + Δx, y) — f(x, y), называемое частным приращением функции z по переменной x.
Аналогично, Δyz = f(x , y + Δy) — f(x, y) называют частным приращением функции z по переменной y.
если они существуют, называются частными производными функции z = f(x, y) по переменным x и y соответственно.
Частная производная вычисляется как производная от функции z = f(x, y) по переменной x при условии, что y = const.
Частная производная вычисляется по y при условии, что x = const.
Все правила и формулы дифференцирования функций одной переменной применимы для нахождения частных производных функции любого числа переменных.
Полным приращением функции z = f(x, y) называется разность
Главная часть полного приращения функции z = f(x, y), линейно зависящая от приращений независимых переменных Δx и Δy, называется полным дифференциалом и обозначается dz. Если функция имеет непрерывные частные производные, то
где dx = Δx, dy = Δy – приращения независимых переменных, называемые их дифференциалами. С точностью до бесконечно малых величин высшего порядка относительно Δx и Δy верно равенство Δz ≈ dz. Последнее применяется для нахождения приближенного значения функции в точке:
Тема 2. Диференцирование сложной и неявно заданнной функции. Производные и дифференциалы высших порядков
4. Частные производные сложных и неявных функций. Полная производная
Функция z = f(u, v), где u = φ(x, y), v = ψ(x, y), называется сложной функцией переменных x, y. Для нахождения частных производных сложных функций используются следующие формулы:
В частности, если x = t, то , и
– формула полной производной.
5. Частные производные второго порядка
Частными производными второго порядка называются частные производные, взятые от частных производных первого порядка:
Частные производныеи
называются смешанными. Значения смешанных производных в точках, в которых они непрерывны, равны между собой:
Тема 3. Некоторые применения частных производных
6. Касательная плоскость и нормаль к поверхности
Прямая называется касательной к поверхности в некоторой точке M0(x; y; z), если она является касательной к какой-нибудь кривой, лежащей на поверхности и проходящей через точку M0.
Плоскость, в которой расположены все касательные прямые к линиям на поверхности, проходящим через данную ее точку M0, называется касательной плоскостью к поверхности в точке M0.
Прямая, проведенная через точку M0 поверхности перпендикулярно к касательной плоскости, называется нормалью к поверхности в точке M0.
Если поверхность задана уравнением F(x, y, z) = 0, то:
а уравнение нормали к поверхности в этой точке:
7. Градиент
Определение . Градиентом функции u (x, y. ) называется вектор, координаты которого есть частные производные функции u по x, y. . Обозначение: grad u.
Градиент в данной точке M0 находим, подставляя координаты точки M0:
8. Производная по направлению
Дадим характеристику скорости роста функции F(x, y, z) по направлению от точки M0 к точке M, т.е. по направлению вектора
Опр . Производной функции F по направлению вектора называется функция
Функция F в направлении вектора: возрастает, если
, убывает, если
, не меняется при
.
Производную проще вычислять как скалярное произведение
9. Экстремумы функции двух переменных
Точка M0(x0; y0) из области определения D функции z = f(x, y) называется точкой минимума функции, если z = f(x0, y0) Теорема (достаточные условия экстремума). Пусть в некоторой области, содержащей точку M0(x0; y0), функция z = f(x, y) имеет непрерывные частные производные до третьего порядка включительно.
Источник





