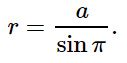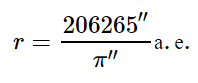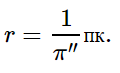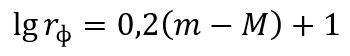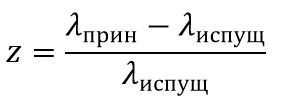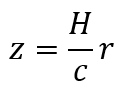Фотометрический способ определения расстояния

Реферат: Определение расстояний до звезд и планет

Определение расстояний до космических объектов. 3

Определение расстояний до планет. 4

Определение расстояний до ближайших звезд. 4

Метод параллакса. . 4

Фотометрический метод определения расстояний. . 6

Определение расстояния по относительным скоростям. . 7

Список литературы. 9

Вступление.

Наши знания о Вселенной тесно связаны со способностью человека определять расстояния в пространстве. С незапамятных времен вопрос «как далеко?» играл первостепенную роль для астронома в его попытках познать свойства Вселенной, в которой он живет. Но как бы ни было велико стремление человека к познанию, оно не могло быть осуществлено до тех пор, пока в распоряжении людей не оказались высокочувствительные и совершенные инструменты. Таким образом, хотя на протяжении веков представления о физическом мире непрерывно развивались, завесы, скрывавшие верстовые столбы пространства, оставались нетронутыми. Во все века философы и астрономы размышляли о космических расстояниях и усердно искали способы их измерения. Но все было напрасно, так как необходимые для этого инструменты не могли быть изготовлены. И, наконец, после того как телескопы уже в течение многих лет использовались астрономами и первые гении посвятили свой талант изучению богатств, добытых этими телескопами, настало время союза точной механики и совершенной оптики, который позволил создать инструмент, способный разрешить проблему расстояний. Барьеры были устранены, и многие астрономы объединили свои знания, мастерство и интуицию с целью определить те колоссальные расстояния, которые отделяют от нас звездные миры.

В 1838 году три астронома (в разных частях света) успешно измерили расстояния до некоторых звезд. Фридрих Вильгельм Бессель в Германии определил расстояние до звезды Лебедь 61. Выдающийся русский астроном Василий Струве установил расстояние до звезды Веги. На мысе Доброй Надежды в Южной Африке Томас Гендерсон измерил расстояние до ближайшей к Солнцу звезды – альфа Центавра. Во всех названных случаях астрономы измеряли невообразимо малое угловое расстояние, чтобы определить так называемый параллакс. Их успех был обусловлен тем, что звезды, до которых они измеряли расстояния, находились относительно близко к Земле.

Определение расстояний до космических объектов.

В астрономии нет единого универсального способа определения расстояний. По мере перехода от близких небесных тел к более далеким одни методы определения расстояний сменяют другие, служащие, как правило, основой для последующих. Точность оценки расстояний ограничивается либо точностью самого грубого из методов, либо точностью измерения астрономической единицы длины (а. е.), величина которой по радиолокационным измерениям известна со среднеквадратичной погрешностью 0,9 км. и равна 149597867,9 ± 0,9 км. С учетом различных изменений а. е. Международный астрономический союз принял в 1976 году значение 1 а. е. = 149597870 ± 2 км.

Определение расстояний до планет.

Название: Определение расстояний до звезд и планет Раздел: Рефераты по авиации и космонавтике Тип: реферат Добавлен 04:40:15 08 июня 2004 Похожие работы Просмотров: 1499 Комментариев: 20 Оценило: 7 человек Средний балл: 4.6 Оценка: 5 Скачать

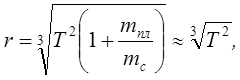Среднее расстояние r планеты от Солнца (в долях а. е.) находят по периоду ее обращения Т :

где r выражено в а. е., а Т – в земных годах. Массой планеты m по сравнению с массой солнца m_c можно пренебречь. Формула следует из третьего закона Кеплера (квадраты периодов обращения планет вокруг Солнца относятся как кубы их средних расстояний от Солнца).

Расстояния до Луны и планет с высокой точностью определены также методами радиолокации планет.

Определение расстояний до ближайших звезд.

Метод параллакса.

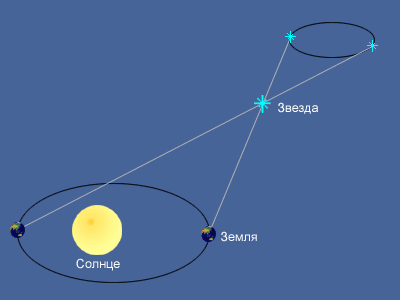
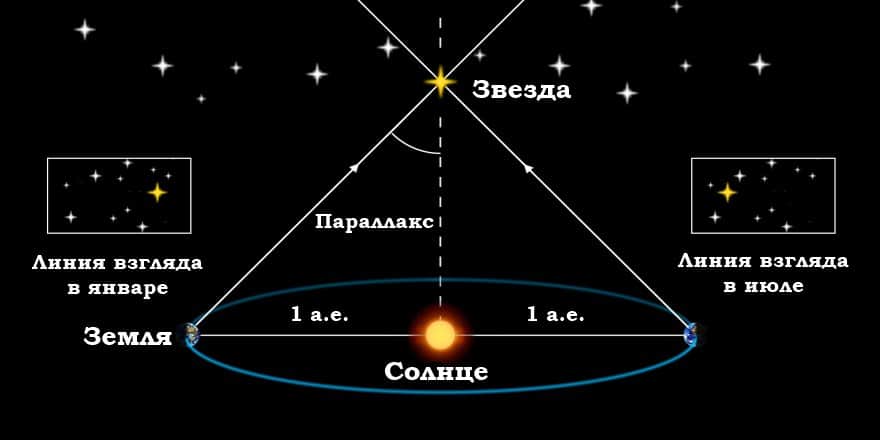
Вследствие годичного движения Земли по орбите близкие звезды немного перемещаются относительно далеких «неподвижных» звезд. За год такая звезда описывает на небесной сфере малый эллипс, размеры которого тем меньше, чем звезда дальше. В угловой мере большая полуось этого эллипса приблизительно равна величине максимального угла, под каким со звезды видна 1 а. е. (большая полуось земной орбиты), перпендикулярная направлению на звезду. Этот угол (p), называемый годичным или тригонометрическим параллаксом звезды, равный половине ее видимого смещения за год, служит для измерения расстояния до нее на основе тригонометрических соотношений между сторонами и углами треугольника ЗСА, в котором известен угол p и базис – большая полуось земной орбиты (см. рис. 1).

Расстояние r до звезды, определяемое по величине ее тригонометрического параллакса p, равно:

где параллакс p выражен в угловых секундах.

Для удобства определения расстояний до звезд с помощью параллаксов в астрономии применяют специальную единицу длины – парсек (пс). Звезда, находящаяся на расстоянии 1 пс, имеет параллакс, равный 1». Согласно вышеназванной формуле, 1 пс = 206265 а. е. = 3,086·10 18 см.

Наряду с парсеком применяется еще одна специальная единица расстояний – световой год (т. е. расстояние, которое свет проходит за 1 год), он равен 0,307 пс, или 9,46·10 17 см.

Ближайшая к Солнечной системе звезда – красный карлик 12-й звездной величины Проксима Центавра – имеет параллакс 0,762, т. е. расстояние до нее равно 1,31 пс (4,3 световых года).

Нижний предел измерения тригонометрических параллаксов

0,01», поэтому с их помощью можно измерять расстояния, не превышающие 100 пс с относительной погрешностью 50%. (При расстояниях до 20 пс относительная погрешность не превышает 10%.) Этим методом до настоящего времени определены расстояния до около 6000 звезд. Расстояния до более далеких звезд в астрономии определяют в основном фотометрическим методом.

Источник

Определение расстояний до ближайших звезд.

Вследствие годичного движения Земли по орбите близкие звезды немного перемещаются относительно далеких «неподвижных» звезд. За год такая звезда описывает на небесной сфере малый эллипс, размеры которого тем меньше, чем дальше звезда. В угловой мере большая полуось этого эллипса приблизительно равна величине макс. угла, под каким со звезды видна 1 а.е. (большая полуось земной орбиты), перпендикулярная направлению на звезду. Этот угол (), называемый годичным или тригонометрическим параллаксом звезды, служит для измерения расстояния до нее на основе тригонометрических соотношений между сторонами и углами треугольника ЗСА, в к-том известен угол и базис — большая полуось земной орбиты (рис. 2).

Расстояние r до звезды, определяемое по величине ее тригонометрического параллакса , равно:

(а.е.), (5)

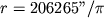
где параллакс выражен в угловых секундах.

Рис. 2. Определение расстояния до звезды А по ее

видимому годичному перемещению на небесной сфере,

вызванному движением Земли по орбите; — параллакс

звезды А, С — Солнце, З — Земля, расстояние между

ними равно 1 а.е.

Для удобства определения расстояний до звезд с помощью параллаксов в астрономии применяют специальную единицу длины — парсек (пк). Звезда, находящаяся на расстоянии 1 пк, имеет параллакс, равный 1″. Согласно формуле (5), 1 пк=206265 а.е.= см. Наряду с парсеком применяется еще одна специальная единица расстояний — световой год, он равен 0,307 пк, или см.

Ближайшая к Солнечной системе звезда — красный карлик 12-й звездной величины Проксима Центавра — имеет параллакс 0,762, т.е. расстояние до нее равно 1,32 пк (4,3 св. года).

Нижний предел измерений тригонометрических параллаксов

0,01″, поэтому с их помощью можно измерять расстояния, не превышающие 100 пк (с относительной погрешностью 50%). При расстояниях до 20 пк относительная погрешность не превышает 10%. Расстояния до более далеких звезд в астрономии определяют в основном фотометрическим методом (см. ниже).

Кроме параллактических смещений близких звезд можно отметить лишь два случая, когда видимые перемещения деталей космических объектов по небу можно также использовать для точного определения расстояний до них. Это — несколько движущихся близких звездных скоплений и быстро перемещающиеся газовые оболочки или сгущения. Примером являются новые и сверхновые звезды, для разлетающихся оболочек которых наряду с видимой скоростью расширения в угловых секундах можно определить спектроскопическим способом радиальную скорость расширения.

Фотометрический метод определения расстояний.

Освещенности, создаваемые одинаковыми по мощности источниками света, обратно пропорциональны квадратам расстояний до них. Следовательно, видимый блеск одинаковых светил (т.е. освещенность, создаваемая у Земли на единичной площадке, перпендикулярной лучам света) может служить мерой расстояний до них. Выражение освещенностей в звездных величинах (m — видимая, M — абсолютная звездная величина) приводит к следующей основной формуле фотометрических расстояний r_ф (пк):

(6)

Для светил, у которых известны тригонометрические параллаксы, можно, определив M по этой же формуле, сопоставить физические свойства с абсолютными звездными величинами. Это сопоставление показало, что абсолютные звездные величины многих классов светил (звезд, галактик и др.) можно оценивать по ряду их физических свойств.

Основным способом оценки абсолютных величин звезд является спектральный способ: в спектрах звезд одного и того же спектрального класса обнаружены особенности, указывающие на их абсолютные величины (чаще всего это усиление линий ионизованных атомов с возрастанием светимости звезд). По таким признакам звезды разделены на классы светимости (см. Светимости классы). По классам и более мелким подклассам светимости, оцениваемым по спектрам звезд, можно находить абсолютные величины с погрешность до 0,5 m . Эта погрешность соответствует относительной погрешности 30% при определении r_ф по формуле (6).

Для определения расстояний до звездных скоплений имеется спец. способ, использующий диаграмму «видимая величина-показать цвета» звезд скопления. Она сравнивается с диаграммой «абсолютная величина-показать цвета», которая составлена по звездам того же типа близких к нам скоплений (рис. 3). Сдвиг между сравниваемыми диаграммами по вертикали равен модулю расстояния (m-M), по которому при помощи формулы (6) и находят т.н. фотометрические расстояние r_ф звездного скопления (с относительной погрешностью 20%).

Рис. 3. Зависимость «абсолютная звездная

величина MV-показатель цвета (B-V)₀» для исходной

главной последовательности (верхняя кривая)

и зависимость «видимая звездная величина

m₀ — показатель цвета» скопления Персея (нижняя кривая);

m₀ — видимая звездная величина, свободная от

межзвездного поглощения света. Сдвиг по оси

звездных величин равен модулю расстояний (m₀-M_V).

Важный метод определения фотометрических расстояний в Галактике и до соседних звездных систем — галактик — основан на характерном свойстве переменных звезд — цефеид. Короткопериодические цефеиды (с периодами колебаний блеска менее суток) в среднем имеют абсолютную величину +0,5 m . Они встречаются в шаровых звездных скоплениях, в центральной области и сферической короне Галактики и относятся к ее звездному населению II типа. По цефеидам в конечном счете найдены расстояния до шаровых звездных скоплений и установлено расстояние от Солнца до центра Галактики.

Для долгопериодических цефеид (периоды колебаний от 1 до 146 сут.), относящихся к звездному населению I типа (плоской составляющей Галактики), установлена важная зависимость период-светимость, согласно которой, чем короче период колебаний блеска, тем цефеида слабее по абсолютной величине. С помощью этой зависимости можно определить абсолютные величины цефеид по длительности их периодов колебаний блеска и, следовательно, фотометрические расстояния до цефеид и звездных скоплений, спиральных рукавов и звездных систем, где они наблюдаются (см. Период-светимость зависимость). Погрешность определения расстояний по цефеидам составляет для звездных скоплений в среднем 40% (в отдельных случаях меньше).

Источник

Фотометрический способ определения расстояния

Методы определения расстояний до звезд

Годичный параллакс

Кажущееся перемещение более близкой звезды на фоне очень далеких звезд происходит по эллипсу с периодом в 1 год и отражает движение наблюдателя вместе с Землей вокруг Солнца. Маленький эллипс, описываемый звездой, называется параллактическим эллипсом. В угловой мере большая полуось этого эллипса равна величине угла, под которым со звезды видна большая полуось земной орбиты, перпендикулярная направлению на звезду. Этот угол называется годичным параллаксом ( π ).

Параллактические смещения звезд служат неопровержимым доказательством обращения Земли вокруг Солнца. Расстояния до звезд определяются по их годичному параллактическому смещению, которое обусловлено перемещением наблюдателя (вместе с Землей) по земной орбите.

Если CT = a есть средний радиус земной орбиты, SC = r — расстояние до звезды S от Солнца C, а угол π — годичный параллакс звезды, то

Так как годичные параллаксы звезд оцениваются десятичными долями секунды, а 1 радиан равен 206265′′ , то расстояние до звезды можно определить из соотношения

При измерении расстояний до звезд астрономическая единица слишком мала. Поэтому для удобства определения расстояний до звезд в астрономии применяется специальная единица длины — парсек (пк) , название которой происходит от слов «параллакс» и «секунда».

Парсек — это расстояние, с которого радиус земной орбиты был бы виден под углом в 1′′.

1 пк = 206 265 а. е. = 3,086 · 10 13 км.

Таким образом, расстояние до звезд в парсеках будет определяться выражением

В астрономических единицах обычно выражаются расстояния до тел Солнечной системы. Расстояния до небесных тел, находящихся за пределами Солнечной системы, обычно выражаются в парсеках, килопарсеках ( 1 кпк = 10 3 пк ) и мегапарсеках ( 1 Мпк = 10 6 пк ), а также в световых годах ( 1 св. г. = 9,46 · 10 12 км = 63 240 а. е. = 0,3067 пк или 1 пк = 3,26 св. г. ).

Световой год — расстояние, которое электромагнитное излучение (в вакууме) проходит за 1 год.

Фотометрический метод определения расстояний

Освещенности, создаваемые одинаковыми по мощности источниками света, обратно пропорциональны квадратам расстояний до них. Следовательно, видимый блеск одинаковых светил (т.е. освещенность, создаваемая у Земли на единичной площадке, перпендикулярной лучам света) может служить мерой расстояний до них. Выражение освещенностей в звездных величинах ( m — видимая, M — абсолютная звездная величина) приводит к следующей основной формуле фотометрических расстояний r_ф(пк) :

Для светил, у которых известны тригонометрические параллаксы, можно, определив M по этой же формуле, сопоставить физические свойства с абсолютными звездными величинами. Это сопоставление показало, что абсолютные звездные величины многих классов светил (звезд, галактик и др.) можно оценивать по ряду их физических свойств.

Основным способом оценки абсолютных величин звезд является спектральный способ: в спектрах звезд одного и того же спектрального класса обнаружены особенности, указывающие на их абсолютные величины (чаще всего это усиление линий ионизованных атомов с возрастанием светимости звезд). По таким признакам звезды разделены на классы светимости. По классам и более мелким подклассам светимости, оцениваемым по спектрам звезд, можно находить абсолютные величины с погрешность до 0,5 m . Эта погрешность соответствует относительной погрешности 30%.

Цефеиды (стандартные свечи)

Важный метод определения фотометрических расстояний в Галактике и до соседних звездных систем — галактик — основан на характерном свойстве переменных звезд — цефеид. Короткопериодические цефеиды (с периодами колебаний блеска менее суток) в среднем имеют абсолютную величину +0,5 m . Они встречаются в шаровых звездных скоплениях, в центральной области и сферической короне Галактики и относятся к ее звездному населению II типа. По цефеидам в конечном счете найдены расстояния до шаровых звездных скоплений и установлено расстояние от Солнца до центра Галактики.

Для долгопериодических цефеид (периоды колебаний от 1 до 146 сут.), относящихся к звездному населению I типа (плоской составляющей Галактики), установлена важная зависимость период-светимость, согласно которой, чем короче период колебаний блеска, тем цефеида слабее по абсолютной величине. С помощью этой зависимости можно определить абсолютные величины цефеид по длительности их периодов колебаний блеска и, следовательно, фотометрические расстояния до цефеид и звездных скоплений, спиральных рукавов и звездных систем, где они наблюдаются. Погрешность определения расстояний по цефеидам составляет для звездных скоплений в среднем 40% (в отдельных случаях меньше).

Определение внегалактических расстояний

Расстояния до ближайших галактик были установлены по оценкам видимых звездных величин цефеид и ярчайших звезд в этих звездных системах. Более тысячи цефеид найдено в Магеллановых Облаках, несколько сотен — в Туманности Андромеды (М31). Цефеиды обнаружены также в семи неправильных и спиральных галактиках, находящихся в радиусе около 3 Мпк вокруг нашей Галактики.

В системах, где не удается обнаружить цефеиды, ищут ярчайшие звезды-сверхгиганты и гиганты высших классов светимости. Ярчайшие сверхгиганты обнаружены в нескольких сотнях спиральных и неправильных галактик в радиусе до 10 Мпк (абсолютные величины их — от -9 до -10 m ). В эллиптических галактиках население I типа (долгопериодические цефеиды, сверхгиганты и горячие газовые туманности) отсутствует. Однако небольшие эллиптические галактики нашей Местной группы на фотографиях распадаются на звезды, ярчайшие из которых оказались красными гигантами, аналогичными гигантам в шаровых звездных скоплениях нашей Галактики (абсолютные величины этих гигантов достигают -2 m , радиус обнаружения — около 1 Мпк). По красным гигантам удается оценивать фотометрические расстояния до эллиптических галактик внутри Местной группы галактик с погрешностью 20%.

В качестве индикаторов расстояний используются также новые звезды и сверхновые звезды.

В некоторых галактиках наблюдаются яркие газовые туманности. Оказалось, что линейные размеры наибольших туманностей в галактиках почти одинаковы. Поэтому, измерив угловые размеры d» ярчайшей туманности в какой-либо галактике, можно определить расстояние r до этой галактики. Данный способ применим к спиральным и неправильным галактикам до расстояний 15 Мпк. Погрешность этого метода — не менее 10%.

До остальных галактик фотометрические расстояния можно определять более грубым способом по оценке интегральной звездной величины галактики. По особенностям внешнего вида спиральных галактик (толщина, длина спиральных рукавов, поверхностная яркость и т.п.) часто можно грубо оценить светимость галактики или, по крайней мере, установить, что галактика не относится к числу карликовых. В последнем случае ее абсолютную интегральную величину можно условно принять равной -20 m (ср. значение для галактик-гигантов) и по видимой величине грубо оценить расстояние.

На больших расстояниях (> 1000 Мпк) видимый блеск галактик и других космических объектов ослабляется не только в силу фотометрического закона квадрата расстояния, но также, помимо поглощения света, вследствие красного смещения — «покраснения» далеких источников излучения, отражающего расширение Вселенной, что приходится учитывать при определении фотометрических расстояний.

Определение расстояний по красному смещению

Сравнение фотометрических расстояний до галактик с величиной смещения z их спектральных линий к красному концу спектра показало, что величина

пропорциональна расстоянию r (Хаббла закон):

где H — постоянная Хаббла. Отсюда получается формула для определения расстояний до далеких галактик, радиогалактик и квазаров:

Источник