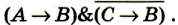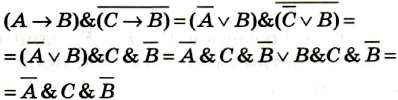Формальный способ решения задач

Урок 27
§22. Логические задачи и способы их решения

Содержание урока:

	22.4. Использование таблиц истинности для решения логических задач
22.3. Задачи на сопоставление. Табличный метод. 22.4. Использование таблиц истинности для решения логических задач		САМОЕ ГЛАВНОЕ Вопросы и задания

22.5. Решение логических задач путём упрощения логических выражений

Следующий формальный способ решения логических задач состоит в том, чтобы:

1) выделить из условия задачи элементарные (простые) высказывания и обозначить их буквами;
2) записать условие задачи на языке алгебры логики, соединив простые высказывания в составные с помощью логических операций;
3) составить единое логическое выражение, учитывающее все требования задачи;
4) используя законы алгебры логики, упростить полученное выражение и вычислить его значение;
5) выбрать решение — набор логических переменных (элементарных высказываний), при котором построенное логическое выражение является истинным;
6) убедиться, что полученное решение удовлетворяет всем условиям задачи.

Пример 7. На вопрос, кто из трёх учащихся изучал логику, был получен ответ: «Если изучал первый, то изучал и второй, но неверно, что если изучал третий, то изучал и второй». Кто из учащихся изучал логику?

Обозначим через А, В, С простые высказывания:

• А = «Первый ученик изучал логику»;
• В = «Второй ученик изучал логику»;
• С = «Третий ученик изучал логику».

Из условия задачи следует истинность высказывания:

Упростим получившееся высказывание:

Получившееся высказывание будет истинным только в случае, если С — истина, а А и В — ложь. А это значит, что логику изучал только третий ученик, а первый и второй не изучали.

Cкачать материалы урока

Источник

ФОРМАЛЬНОЕ РЕШЕНИЕ ЗАДАЧИ

После проведения анализа постановки задачи, выявления данных, их структуры и отношений между ними можно приступить к построению формальной модели. Это наиболее важный этап в процессе решения задачи.

Модель — это упрощенное представление о реальном объекте, процессе или явлении. Моделирование — построение моделей для исследования и изучения моделируемого объекта, процесса, явления с целью получения новой информации при решении конкретных задач.

Для описания модели предметной области решаемой задачи необходимо выбрать некоторую формальную систему. Обычно, исходя из постановки задачи, можно сразу определить один или несколько видов моделей, подходящих для описания и моделирования решения вашей задачи: математические, геометрические, структурные, логические и др.

Наиболее распространенными и хорошо изученными являются математические модели, описывающие зависимости между данными числового типа. Например, в качестве математической модели звезды можно использовать систему уравнений, описывающих процессы, происходящие в недрах звезды. Математической моделью другого рода являются математические соотношения, позволяющие рассчитать оптимальный план работы предприятия. К основным достоинствам математических моделей безусловно относятся хорошо изученные и широко применяемые математические методы решения большого класса задач, что значительно облегчает формирование основной идеи и выбор методов решения задачи.

Приступая к разработке модели, следует попытаться решить задачу для конкретных входных данных, затем обобщить полученное решение на основе его анализа для любых значений входных данных. Перед тем как определить решение задачи для конкретных входных данных целесообразно найти ответ на следующие вопросы:

Существуют ли решения аналогичных задач?

Какая математическая модель больше всего подходит для решения этой задачи?

Пример 1.Постановка задачи. Требуется определить пригодность данной аудитории для проведения учебных занятий.

Этап 1. Анализ постановки задачи и ее предметной области.

В результате анализа предметной области, выявляем, что эта предметная область связана с образовательным процессом. И постановка задачи может быть переформулирована следующим образом. Определить, подходит ли некоторая аудитория для проведения занятий группы учеников при некоторой норме площади для каждого ученика. Введем обозначения для входных и выходных данных. Исходные данные должны быть представлены простыми переменными значениями числового типа: А — ширина аудитории, B — ее длина, К — количество учеников в группе, N — допустимое минимальное количество квадратных метров для одного ученика (норма ), M — количество парт в аудитории. В качестве выходных данных будут выступать сообщения: » Аудитория может быть использована для поведения учебных занятий » и » Аудитория не может быть использована для поведения учебных занятий «.

Этап 2. Формальное решение.

Определим отношения между входными и выходными данными. Для этого введем промежуточные данные числового типа : S — площадь аудитории, C — требуемая по нормам площадь для проведения занятий для группы из К учеников, D — требуемое количество парт для обучения группы, состоящей из К учеников. Опишем соотношения между входными и выходными данными, используя математические зависимости. Математическая модель:

Дата добавления: 2016-04-06 ; просмотров: 844 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник

Как решать логические и математические задачи

Решение задач на логику — отличная гимнастика для ума детей и взрослых на каждый день. На ЛогикЛайк более 3500 заданий с ответами и пояснениями, полноценный учебный комплекс для развития логики и способностей к математике.

Решаем логические задачи

Чтобы научиться решать типовые логические задачи, простые и нестандартные математические задачи, важно знать основные приемы и методы их решения. Ведь решить одну и ту же задачу и прийти к правильному ответу во многих случаях можно разными способами.

Знание и понимание различных методов решения поможет определить, какой способ подойдет лучше в каждом конкретном случае, чтобы выбрать наиболее быстрый и простой путь получения ответа.

К «классическим» логическим задачам относятся текстовые задачи, цель решения которых состоит в распознавании объектов или расположении их в определенном порядке в соответствии с заданными условиями.

Более сложными и увлекательными типами заданий являются задачи, в которых отдельные утверждения являются истинными, а другие ложными. Задачи на перемещение, перекладывание, взвешивание, переливание — самые яркие примеры широкого ряда нестандартных задач на логику.

Основные методы решения логических задач

• метод рассуждений;
• с помощью таблиц истинности;
• метод блок-схем;
• средствами алгебры логики (алгебры высказываний);
• графический (в том числе, «дерево логических условий», метод кругов Эйлера);
• метод математического бильярда.

Давайте рассмотрим подробнее с примерами три популярных способа решения логических задач, которые мы рекомендуем использовать в начальной школе (детям 6-12 лет):

• метод последовательных рассуждений;
• разновидность метода рассуждений — «с конца»;
• табличный способ.

Метод последовательных рассуждений

Самый простой способ решения несложных задач заключается в последовательных рассуждениях с использованием всех известных условий. Выводы из утверждений, являющихся условиями задачи, постепенно приводят к ответу на поставленный вопрос.

На столе лежат Голубой , Зеленый , Коричневый и Оранжевый карандаши.

Третьим лежит карандаш, в имени которого больше всего букв. Голубой карандаш лежит между Коричневым и Оранжевым .

Разложи карандаши в описанном порядке.

Рассуждаем. Последовательно используем условия задачи для формулирования выводов о позиции, на которой должен лежать каждый следующий карандаш.

• Больше всего букв в слове «коричневый», значит, он лежит третьим.
• Известно, что голубой карандаш лежит между коричневым и оранжевым. Справа от коричневого есть только одна позиция, значит, расположить голубой между коричневым и другим карандашом возможно только слева от коричневого.
• Следующий вывод на основе предыдущего: голубой карандаш лежит на второй позиции, а оранжевый — на первой.
• Для зеленого карандаша осталась последняя позиция — он лежит четвертым.

Метод «с конца»

Такой способ решения является разновидностью метода рассуждений и отлично подходит для задач, в которых нам известен результат совершения определенных действий, а вопрос состоит в восстановлении первоначальной картины.

Бабушка испекла для троих внуков рогалики и оставила их на столе. Коля забежал перекусить первым. Сосчитал все рогалики, взял свою долю и убежал.
Аня зашла в дом позже. Она не знала, что Коля уже взял рогалики, сосчитала их и, разделив на троих, взяла свою долю.
Третьим пришел Гена, который тоже разделил остаток выпечки на троих и взял свою долю.
На столе осталось 8 рогаликов.

Сколько рогаликов из восьми оставшихся должен съесть каждый, чтобы в результате все съели поровну?

Начинаем рассуждение «с конца».
Гена оставил для Ани и Коли 8 рогаликов (каждому по 4). Получается, и сам он съел 4 рогалика: 8 + 4 = 12.
Аня оставила для братьев 12 рогаликов (каждому по 6). Значит, и сама она съела 6 штук: 12 + 6 = 18.
Коля оставил ребятам 18 рогаликов. Значит, сам съел 9: 18 + 9 = 27.

Бабушка положила на стол 27 рогаликов, рассчитывая, что каждому достанется по 9 штук. Поскольку Коля уже съел свою долю, Аня должна съесть 3, а Гена — 5 рогаликов.

Решение логических задач с помощью таблиц истинности

Суть метода состоит в фиксации условий задачи и полученных результатов рассуждений в специально составленных под задачу таблицах. В зависимости от того, является высказывание истинным или ложным, соответствующие ячейки таблицы заполняются знаками «+» и «-» либо «1» и «0».

Три спортсмена ( красный , синий и зеленый ) играли в баскетбол.
Когда мяч оказался в корзине, красный воскликнул: «Мяч забросил синий».
Синий возразил: «Мяч забросил зеленый».
Зеленый сказал: «Я не забрасывал».

Кто забросил мяч, если только один из троих сказал неправду?

Сначала таблицу составляют: слева записывают все утверждения, которые содержатся в условии, а сверху — возможные варианты ответа.

Затем таблицу последовательно заполняют: верные утверждения отмечают знаком «+», а ложные утверждения — знаком «-«.

Рассмотрим первый вариант ответа («мяч забросил красный «), проанализируем утверждения, записанные слева, и заполним первый столбик.
Исходя из нашего предположения («мяч забросил красный «), утверждение «мяч забросил синий» — ложь. Ставим в ячейке «-«.
Утверждение «мяч забросил зеленый» также ложь. Заполняем ячейку знаком «-«.
Утверждение зеленого «Я не забрасывал» – истина. Ставим в ячейке «+».

Рассмотрим второй вариант ответа (предположим, что мяч забросил зеленый ) и заполним второй столбик.
Утверждение «мяч забросил Синий» — ложь. Ставим в ячейке «-«.
Утверждение «мяч забросил зеленый « — истина. Заполняем ячейку знаком «+».
Утверждение зеленого «Я не забрасывал» – ложь. Ставим в ячейке «-«.

И, наконец, третий вариант: предположим, что «мяч забросил синий «.
Тогда утверждение «мяч забросил синий « — истина. Ставим в ячейке «+».
Утверждение «мяч забросил зеленый» — ложь. Заполняем ячейку знаком «-«. Утверждение зеленого «Я не забрасывал» – истина. Ставим в ячейке «+».

Так как по условию лишь один из троих ребят сказал неправду, в заполненной таблице выбираем такой вариант ответа, где будет только одно ложное утверждение (в столбце один знак «-«). Подходит третий столбец.

Значит, правильный ответ – мяч забросил синий.

Метод блок-схем

Метод блок-схем считается оптимальным вариантом для решения задач на взвешивание и на переливание жидкостей. Альтернативный способ решения этого типа задач — метод перебора вариантов — не всегда является оптимальным, да и назвать его системным довольно сложно.

• графически (блок-схемой) описываем последовательность выполнения операций;
• определяем порядок их выполнения;
• в таблице фиксируем текущие состояния.

Подробнее об этом и других способах решения логических задач с примерами и описанием хода решения мы рассказываем в полном Курсе ЛогикЛайк по развитию логического мышления.

Отгадывайте самые интересные загадки на логику, собранные специально для постоянных читателей нашего блога и учеников LogicLike, решайте логические задачи онлайн вместе с тысячами детей и взрослых!

Учим детей 5-12 лет решать любые логические и математические задачи. Более 3500 занимательных заданий с ответами и пояснениями.

Источник

Формальный способ решения задач

Из анализа специальной литературы мы выделяем несколько различных способов решения логических задач:

• Метод рассуждений;
• Метод таблиц;
• Метод блок-схем;
• Метод графов;
• Метод кругов Эйлера.

Остановимся отдельно на каждом из выделенных методов, иллюстрируя их примерами решения конкретных задач.

Метод первый: Метод рассуждений

Идея метода состоит в том, что мы проводим рассуждения, используя последовательно все условия задачи, и приходим к выводу, который и будет являться ответом задачи. Этим способом обычно решают несложные логические задачи.

Например. Возраст мамы и дочки в сумме составляет 98 лет. Дочь родилась, когда маме было 22 года. Сколько лет маме и дочке? Решение: так как разница в их возрасте 22 года (именно в этом возрасте у мамы родилась дочь), то 98 – 22 =76 (лет). Это удвоенный возраст дочери, тогда 76 : 2 = 38(лет). Значит, матери 98 – 38 = 60 (лет).

Задача 1. Вадим, Сергей и Михаил изучают различные иностранные языки: китайский, японский и арабский. На вопрос, какой язык изучает каждый из них, один ответил: «Вадим изучает китайский, Сергей не изучает китайский, а Михаил не изучает арабский». Впоследствии выяснилось, что в этом ответе только одно утверждение верно, а два других ложны. Какой язык изучает каждый из молодых людей?

Решение: Имеется три утверждения. Если верно первое утверждение, то верно и второе, так как юноши изучают разные языки. Это противоречит условию задачи, поэтому первое утверждение ложно. Если верно второе утверждение, то первое и третье должны быть ложны. При этом получается, что никто не изучает китайский. Это противоречит условию, поэтому второе утверждение тоже ложно. Остается считать верным третье утверждение, а первое и второе — ложными. Следовательно, Вадим не изучает китайский, китайский изучает Сергей.

Ответ: Сергей изучает китайский язык, Михаил — японский, Вадим — арабский .

Метод второй: Метод таблиц

Основной прием, который используется при решении текстовых логических задач, заключается в построении таблиц. Таблицы не только позволяют наглядно представить условие задачи или ее ответ, но в значительной степени помогают делать правильные логические выводы в ходе решения задачи. [5]

Идея метода: оформлять результаты логических рассуждений в виде таблицы.

2)возможность контролировать процесс рассуждений;

3)возможность формализовать некоторые логические рассуждения.

Задача 2 . Данным способом можно решить, известную многим загадку Эйнштейна.

5 разных человек в 5 разных домах разного цвета, курят 5 разных марок сигарет, выращивают 5 разных видов животных, пьют 5 разных видов напитков.

Вопрос:1) Кто выращивает рыбок?

2)Норвежец живет в первом доме.

3)Англичанин живет в красном доме.

4)Зеленый дом находится непосредственно слева от белого.

5)Датчанин пьет чай.

6)Тот, кто курит Rothmans, живет рядом с тем, кто выращивает кошек.

7)Тот, кто живет в желтом доме, курит Dunhill.

8)Немец курит Marlboro.

9)Тот, кто живет в центре, пьет молоко.

10)Сосед того, кто курит Rothmans, пьет воду.

11)Тот, кто курит Pall Mall, выращивает птиц.

12)Швед выращивает собак.

13)Норвежец живет рядом с синим домом.

14)Тот, кто выращивает лошадей, живет в синем доме.

15)Тот, кто курит Philip Morris, пьет пиво.

16)В зеленом доме пьют кофе.

Метод третий: Метод блок-схем

Этот метод используют в основном для задач, в которых с помощью сосудов известных емкостей требуется отмерить некоторое количество жидкости, а также задачи, связанные с операцией взвешивания на чашечных весах. Простейший прием решения задач этого класса состоит в переборе возможных вариантов. Понятно, что такой метод решения не совсем удачный, в нем трудно выделить какой-либо общий подход к решению других подобных задач.

Более систематический подход к решению задач «на переливание» заключается в использовании блок-схем. Суть этого метода состоит в следующем. Сначала выделяются операции, которые позволяют нам точно отмерять жидкость. Эти операции называются командами. Затем устанавливается последовательность выполнения выделенных команд. Эта последовательность оформляется в виде схемы. Подобные схемы называются блок-схемами и широко используются в программировании. Составленная блок-схема является программой, выполнение которой может привести нас к решению поставленной задачи. Для этого достаточно отмечать, какие количества жидкости удается получить при работе составленной программы. При этом обычно заполняют отдельную таблицу, в которую заносят количество жидкости в каждом из имеющихся сосудов. [4]

Идея метода: описать последовательность выполнения операций, определить порядок их выполнения и фиксировать состояния.

Задача 3 . Имеются два сосуда — трехлитровый и пятилитровый. Нужно, пользуясь этими сосудами, получить 1, 2, 3, 4, 5, 6, 7 и 8 литров воды. В нашем распоряжении водопроводный кран и раковина, куда можно выливать воду.

Решение. Перечислим все возможные операции, которые могут быть использованы нами, и введем для них следующие сокращенные обозначения: НБ — наполнить больший сосуд водой из-под крана; НМ — наполнить меньший сосуд водой из-под крана; ОБ — опорожнить больший сосуд, вылив воду в раковину; ОМ — опорожнить меньший сосуд, вылив воду в раковину; Б→М — перелить из большего в меньший, пока больший сосуд не опустеет или меньший сосуд не наполнится; М→Б — перелить из меньшего в больший, пока меньший сосуд не опустеет или больший сосуд не наполнится. Выделим среди перечисленных команд только три: НБ, Б→М, ОМ. Кроме этих трех команд рассмотрим еще две вспомогательные команды: Б = 0 ? — посмотреть, пуст ли больший сосуд; М = З ? — посмотреть, наполнен ли малый сосуд.

В зависимости от результатов этого осмотра мы переходим к выполнению следующей команды по одному из двух ключей — «да» или «нет». Такие команды в программировании принято называть командами «условного перехода» и изображать в блок-схемах в виде ромбика с двумя ключами-выходами.

Договоримся теперь о последовательности выполнения выделенных команд. После Б→М будем выполнять ОМ всякий раз, как меньший сосуд оказывается наполненным, и НБ всякий раз, как больший сосуд будет опорожнен. Последовательность команд изобразим в виде блок-схемы.

Начнем выполнение программы. Будем фиксировать, как меняется количество воды в сосудах, если действовать по приведенной схеме. Результаты оформим в виде таблицы.

Дальше эта последовательность будет полностью повторяться. Из таблицы видим, что количество воды в обоих сосудах вместе образует следующую последовательность: 0, 5, 2, 7, 4, 1, 6, 3, 0 и т.д. Таким образом, действуя по приведенной схеме, можно отмерить любое количество литров от 1 до 7. Чтобы отмерить еще и 8 литров, надо наполнить оба сосуда.

Метод четвертый: метод графов.

Граф — множество точек, изображенных на плоскости (листе бумаги, доске), некоторые пары из которых соединены отрезками. Точки называют вершинами графов, а отрезки — ребрами графов. Выделяя из словесных рассуждений главное — объекты и отношения между ними, графы представляют изучаемые факты в наглядной форме.

Примеры решения логических задач с использованием графов подкупают своей наглядностью и простотой, избавляют от лишних рассуждений, во многих случаях сокращают нагрузку на память. С одной стороны, графы позволяют проследить все логические возможности изучаемой ситуации, с другой, благодаря своей обозримости, помогают в ходе решения задачи классифицировать логические возможности, отбрасывать неподходящие случаи, не доводя до полного перебора всех случаев.
Идея метода: выявление и последовательное исключение логических возможностей, задаваемых условиями задачи.

Задача 4. Три ученицы — Аня, Варя и Клава — на первомайской демонстрации были: одна в крас­ном, другая в белом, третья в синем платье. В вы­сказывании: Аня была в красном платье, Варя не в красном, Клава не в синем — одна часть верна, а две неверны. В каком платье была каждая из уче­ниц?

Решение: Будем исходить из двух возможно­стей: Аня была в красном платье (Ак) и Аня была не в красном (то есть в белом или синем) и изобра­зим эти возможности: первую ребром Ак, а вторую двумя ребрами Ас и Аб, исходящими из одной точки. Если Аня была в красном платье, то в синем могла быть или Варя, или Клава. По­этому к ребру Ак присоединим 2 ребра Вс и Кс. Путь АкВс закончим Кб, а путь АкКс закончим Вб. Но из двух получившихся путей условию задачи ни один не удовлетворяет.

Обратимся ко второй возможности. К ребру Ас присоединим два ребра Вк и Кк, так как в красном платье в этом случае могла быть Варя или Клава. Такие же два ребра присоединим к Аб. Закончить каждый из получившихся путей очень просто: нуж­но присоединить последовательно ребра Кб, Вб, Кс и Вс. Имеем четыре логические возможности, но условию задачи удовлетворяет лишь путь АсВкКб, а остальные три пути — не удовлетворяют. Значит, Аня была в синем платье, Варя — в красном, а Кла­ва—в белом.

Метод пятый: метод кругов Эйлера.

Упростить решение многих логических задач помогают так называемые круги Эйлера, с помощью которых можно изобразить множество элементов, обладающих определенным свойством. Круги Эйлера — геометрическая схема, с помощью которой можно изобразить отношения между подмножествами, для наглядного представления.

Тип задач: Метод кругов Эйлера позволяет графически решать математические задачи, основанные на применении теории множеств.

Формальный способ решения подобных задач:

1. Выделить в тексте задачи рассматриваемые свойства объектов.

2. Заполнить круги Эйлера-Венна, проанализировав соответствие объектов и присущих им свойств.

3. Выбрать решение – набор значений простых высказываний, при котором соответствие объектов и свойств является истинным.

4. Проверить, удовлетворяет ли полученное решение условию задачи.

Преимущества и недостатки данного способа:

Необязательность знания формул и законов алгебры логики

Не подходит для решения сложных задач

Не обладает универсальностью, т.е. предназначен для определенного класса задач

Задача 5 . Каждый из 35 шестиклассников является читателем, по крайней мере, одной из двух библиотек: школьной и районной. Из них 25 человек берут книги в школьной библиотеке, 20 – в районной.

1.Являются читателями обеих библиотек;
2. Не являются читателями районной библиотеки;
3. Не являются читателями школьной библиотеки;
4. Являются читателями только районной библиотеки;
5. Являются читателями только школьной библиотеки?

Решение: Заметим, что первый вопрос является ключевым для понимания и решения данной задачи. Ведь не сразу сообразишь, как получается 20 + 25 = 45 из 35. В первом вопросе звучит подсказка к пониманию условия: есть ученики, которые посещают обе библиотеки. А если условие задачи изобразить на схеме, то ответ на первый вопрос становится очевидным.

1. 20 + 25 – 35 = 10 (человек) – являются читателями обеих библиотек. На схеме это общая часть кругов. Мы определили единственную неизвестную нам величину. Теперь, глядя на схему, легко даем ответы на поставленные вопросы.

2. 35 – 20 = 15 (человек) – не являются читателями районной библиотеки. (На схеме левая часть левого круга)

3. 35 – 25 = 10 (человек) – не являются читателями школьной библиотеки. (На схеме правая часть правого круга)

4. 35 – 25 = 10 (человек) – являются читателями только районной библиотеки. (На схеме правая часть правого круга)

5. 35 – 20 = 15 (человек) – являются читателями только школьной библиотеки. (На схеме левая часть левого круга).

Очевидно, что 2 и 5, а также 3 и 4 – равнозначны и ответы на них совпадают.

Источник