Физика способы определения объема

ГДЗ учебник по физике 7 класс Перышкин. №4 Измерение объема тела. Номер №1

Цель работы:
Научиться определять объём тела с помощью измерительного цилиндра.
Приборы и материалы:
Измерительный цилиндр (мензурка), тела неправильной формы небольшого объёма (гайки, фарфоровые ролики, кусочки металла и др.), нитки.
Указания к работе:
1 . Определите цену деления мензурки.
2 . Налейте в мензурки столько воды, чтобы тело можно было полностью погрузить в воду, и измерьте её объём.
3 . Опустите тело, объём которого надо измерить, в воду, удерживая его за нитку (рис. 201 ), и снова измерьте объём жидкости.
4 . Проделайте опыты, описанные в пунктах 2 и 3, с некоторыми другими имеющимися у вас телами.
5 . Результаты измерений запишите в таблицу 9 .
Дополнительное задание.
Если тело неправильной формы не входить в мензурку, то его объём можно определить с помощью отливного сосуда (рис. 202 ). Перед измерением сосуд наполняют водой до отверстия отливной трубки. При погружении в него тела часть воды, равная объёму тела, выливается. Измерив мензуркой её объём, определяют объём погружённого в жидкость тела.

Таблица 9 .

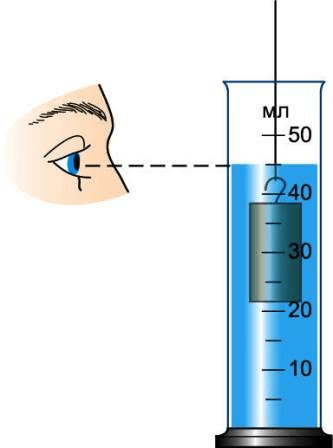
рис. 201

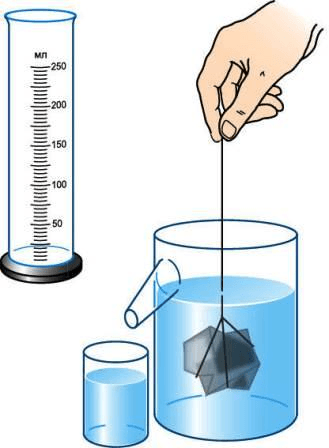
рис. 202

Решение

Объём тела неправильной формы точно измерить с помощью измерительных приборов нельзя. Поэто­му для измерения объема воспользуемся мензуркой. Тело, полностью погружён­ное в жидкость, вытесняет объём жидкости, кото­рый равен объёму самого тела. Воспользуемся этим законом и найдем объёмы некоторых тел следую­щим образом. Нальем достаточное количество воды в мензурку, а затем погрузим полностью туда наше тело. Разница между первоначальным объёмом и объёмом жидкости, в которое погружено тело, равна объёму этого тела.
$V = V_ <2>— V_<1>$ , где $V_<2>$ − объём воды и тела, $V_<1>$ − начальный объём воды в мензурке.

1. Прежде чем проводить измерения физической величины с помощью измерительного прибора нужно определите цену деления его шкалы.
   Для определения цены деления необходимо взять 2 соседних числа, найти их разницу (от большего отнять меньшее), а затем разделить полученное число на количество маленьких штрихов между этими числами.
   На шкале цилиндра возьмём, к примеру, числа 20 и 30 .
   Таким образом, цена каждого деления будет равна
   $\frac<30 - 20><2>= \frac<10><2>$ = 5 мл.
2. В мензурку нальём столько воды, чтобы тело можно было полностью погрузить в воду. Начальный объём воды равен 70 $см^<3>$ .
3. Опустим тело, объём которого надо измерить (шарик, брусок, цилиндр), в воду, удерживая его за нитку, и снова измерим объём жидкости.
   Вычисления.
   $V_ <бр>= 95 — 70 = 25 см^<3>$
   $V_ <ц>= 85 — 65 = 20 см^<3>$
   $V_ <ш>= 75 — 60 = 15 см^<3>$
4. Результаты измерений запишем в таблицу 9 .

№ опыта	Название тела	Начальный объём воды в мензурке $V_<1>, см^<3>$	Объём воды и тела $V_<2>, см^<3>$	Объём тела V, $см^<3>$ $V = V_<2>-V <1>$
1	Брусок	70	95	25
2	Цилиндр	65	85	20
3	Шарик	60	75	15

Вывод. В ходе лабораторной работы мы научились измерять объёмы тел с помощью измерительного цилиндра и выяснили, что объём тел равен разнице объёма воды, в которое погружено тело, и первоначального объёма воды.

Источник

Способы определения объёма тел. Лабораторная работа 4 Урок физики в 7 классе Учебник Пёрышкин А.В. Учитель Кононова Е.Ю. — презентация

Презентация была опубликована 7 лет назад пользователемВадим Шадринцев

Похожие презентации

Презентация 7 класса по предмету «Физика и Астрономия» на тему: «Способы определения объёма тел. Лабораторная работа 4 Урок физики в 7 классе Учебник Пёрышкин А.В. Учитель Кононова Е.Ю.». Скачать бесплатно и без регистрации. — Транскрипт:

1 Способы определения объёма тел. Лабораторная работа 4 Урок физики в 7 классе Учебник Пёрышкин А.В. Учитель Кононова Е.Ю.

2 величинаОбозна- чение Единицы измерения формула Время t с ; мин; ч Длина/высота L / h м ; см; км Путь s Масса m кг; г; мг; т Скорость υм/с ; км/ч υ = s/t ПлощадьS м 2 ; см 2 объёмV м 3 ; см 3 ; мл;V = m/ρ плотностьρ кг/м 3 ; г/см 3 ρ = m/V

3 Запиши и запомни: 1 мл = 1 см 3 1 л = 1 дм 3 1 см 3 = 0,001 дм 3 1 дм 3 =1000 см 3 1см 3 = 0, м 3 1м 3 = см 3

4 § вопрос: способы определить объём тела Ответ: * Вычислить физически: V = m/ρ * Вычислить геометрически: V = abc V = S h *объём тела равен объёму вытесненной жидкости V т = V 2 – V 1 Мензурка отливной стакан

5 Стр.163 Лабораторная работа 4 Измерение объёма тела. Цель: Научиться определять объём тела разными способами; сравнить эти способы. 1 способ физический брусок m б =. г (из Л.Р. 3 ) цилиндр m ц =. г (из Л.Р. 3 ) ρ =. г/см 3 ( из таблицы стр.51) V б = m б /ρ = … / … = … V ц = m ц /ρ = … / … = … (вычислить дома)

6 2 способ: геометрический брусок а = … см ; b = …см; c = … см ( измерить с точностью до десятых) V = abc = … … … = … см 3 ( округлить до целых) (можно вычислять дома) цилиндр h = … см S = … см 2 n ц = 7 V = Sh = … … = … см 3 n н = 11 (округлить до целых) 1 кл = 0.25 см 2 Так можно посчитать площадь: S = (π d 2 ):4 или S = ( n ц + n н /2)0,25 см 2 S = ( 7+ 11/2) 0,25см 2 = 3,125см 2 3см 2

7 3 способ: измерить с помощью мензурки ц.д. = (… — …) : … = … мл ( цена деления ) V 1 = … мл ( объём воды в мензурке ) V 2 = … мл ( объём воды вместе с телом ) V т = V 2 – V 1 = … — … = … мл = … см 3 ( объём тела)

8 4 способ: с помощью отливного стакана и мензурки. Объём тела равен объёму вытесненной жидкости. V т = V ж = … мл = … см 3 ( опишите последовательность действий. Какие сложности возникают при этом способе?)

9 Вывод: ( Ответьте на вопросы) 1) Какой способ определения объёма точнее? 2) Получились ли объёмы одного и того же тела, измеренные разными способами равными? 3) Почему? ( почему равны, или почему различаются.) Дома: доделать Л.Р. 4 ; оформить Л.Р.5

10 8 Цена Деления прибора 9 с как определить цену деления Ц.Д.= -Промежуток между ближайшими делениями шкалы -1)..два оцифрованых деления.. 2) из большего вычесть меньшее 3)разделить на количество промежутков

Источник

Определение площади и объема в физике с примером

Содержание:

Определение площади и объема:

В повседневной жизни нам довольно часто приходится иметь дело с определением таких величин, как площадь и объем. Представьте себе, что вам необходимо сделать ремонт в квартире (или доме): побелить стены и потолок, покрасить пол. Чтобы закупить необходимое количество материалов, нужно определить площадь поверхностей и объем краски.

Из уроков математики вам известно, как находить площадь некоторых фи-гур: квадрата, прямоугольника, параллелограмма.

Рис. 6.1.

Рис. 6.2.

Рис. 6.3

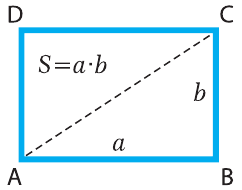
Площадь прямоугольника ABCD (рис. 6.1) вычисляется по формуле:
S = a · b, (6.1)
где a – ширина прямоугольника, b – высота.

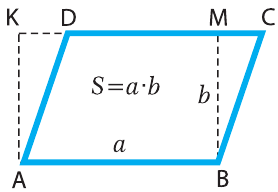
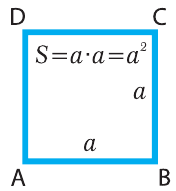
Площадь параллелограмма ABCD (рис. 6.2) также находится по формуле 6.1. Площадь квадрата найти легко, поскольку его ширина и высота одинаковы:
S = a · a = a 2 , (6.2)

Из рис. 6.1 видно, что площадь прямоугольного треугольника АBC можно найти по формуле:
, (6.3)

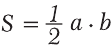
Проблема определения площади круга была решена еще в Древней Греции. Для этого нужно знать радиус круга и число «пи», приблизительное значение
которого π ≈ 3,14.
Площадь круга равняется
S = π · R 2 , (6.4) .

Значение числа 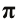можно получить, если разделить длину круга L на его диаметр. Причем не имеет значения, каков размер круга и в каких единицах измерены длина и диаметр (нужно только, чтобы это были одни и те же единицы).

Вычисление объема простых фигур

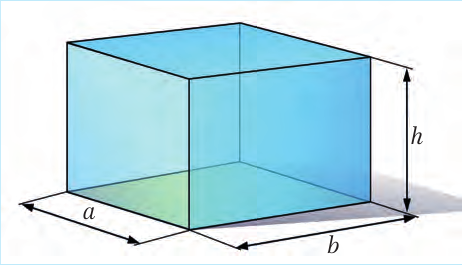
Каждое тело занимает определенный объем. Чем большую часть пространства занимает тело, тем больше его объем. Объем обозначают буквой V (от volume – объем). Чтобы найти объем прямоугольного бруска или ящика (математики называют эту геометрическую фигуру параллелепипедом) со сторона-ми a, b и h, надо их перемножить (рис. 6.4):

Рис. 6.4.

Рис. 6.5.

Рис. 6.6.

V = a · b · h (6.4)
Поскольку S = a · b,
где S – это площадь основания ящика, то формулу (6.4) можно переписать и так:

V = S · h (6.5)
У куба все ребра равны, потому его объем равняется:
V = a · a · a = a 3 (6.6)

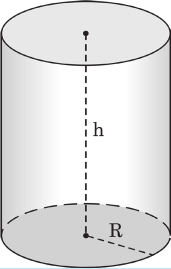
Объем цилиндра (рис. 6.5) с радиусом основания R и высотой h можно также определить по формуле (6.5), то есть:
V = S · h = πR 2 · h (6.7)

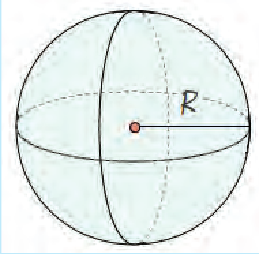
Объем шара (рис. 6.6)
(6.8)

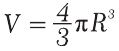
Единицы измерения объема

Поскольку длину сторон измеряют в единицах длины (метр, дециметр, сантиметр и т. д.), то единицы измерения объема – это единицы длины, возведенные в третью степень.

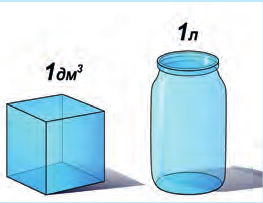
Куб с ребром 1 м имеет объем 1 м 3 (один кубический метр). Один литр (1 л) по определению – это объем куба с ребром 1 дм (рис. 6.7), то есть 1 л = 1 дм 3 (дециметр кубический). Один литр равен 1000 кубических сантиметров: 1 л = 1000 см 3 . Объем в один сантиметр кубический еще называют миллилитром, то есть тысячной частью литра (1 мл = 0,001 л).

Рис. 6.7. Один литр – это 1дм 3

Напомним, что дециметр – это десятая часть метра, а сантиметр – сотая часть метра

Таблица 6.1

1 м 3 = 1 000 л	1 м 3 = 1 000 000 см 3
1 л = 1 дм 3	1 л = 1000 см 3
1 дм 3 = 1 000 см 3	1 л = 1 000 мл
1 см3 = 1 мл	1 мл = 0,001 л

• Заказать решение задач по физике

Измерение объема тел неправильной формы

Прибор для измерения объема называют мензуркой, или мерным цилиндром (рис. 6.8). Мензурка – это прозрачный сосуд с нанесенными делениями, которые обозначают объем в миллилитрах. Дома у вас наверняка есть мерный стакан, то есть та же мензурка. Литровой или поллитровой банкой, или стаканом (250 мл) также можно пользоваться, если не нужна большая точность. С помощью мензурки можно определить объем жидкости и тела неправильной формы. Для этого в мензурку нужно налить воду и определить объем этой воды. Потом полностью погрузить тело в воду и запомнить новое значение объема. Разница измеренных значений равна объему тела.

Рис. 6.8. Деления мензурки определяют объем в миллилитрах (то есть в см 3 )

История:

Существует легенда, согласно которой первым такой способ определения объема изобрел древнегреческий ученый Архимед. Произошло это во время размышлений над довольно сложной зада-чей, предложенной царем Гиероном. Идея решения возникла тогда, когда Архимед влез в ванну и заметил, что уровень воды поднялся. Ученый понял, что вытесненный объем воды как раз равен объему погруженного в нее тела. Восторженный Архимед выпрыгнул из ванны и выбежал на улицу с криком «Эврика! Эврика!», что в переводе с древнегреческого значит «На-шел! Нашел!».

Итоги:

• Площадь тел правильной формы равна произведению основы на высоту и измеряется в квадратных единицах длины S = a · b.
• Объем тел правильной формы определяется как произведение площади основы на высоту и измеряется в кубических единицах V = S · h.
• Объем тел произвольной формы определяют с помощью мензурки
• Площадь круга определяют по формуле S = π · R 2 .
• Объем шара равен .

Рекомендую подробно изучить предметы:

Физика Атомная физика Ядерная физика Квантовая физика Молекулярная физика

Ещё лекции с примерами решения и объяснением:

• Связь физики с другими науками
• Макромир, мегамир и микромир в физике
• Пространство и время
• Что изучает механика в физике
• Единая физическая картина мира
• Физика и научно-технический прогресс
• Физические величины и их единицы измерения
• Точность измерений и погрешности

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник