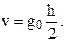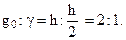Физические способы определения объема ствола

7) Физические способы определение объема ствола.

К физическим способам определения объема ствола относятся ксилометрические и весовые.

Ксилометрические способы базируются на одном из законов Архимеда, согласно которому тело, погруженное в воду, вытесняет равновеликий ее объем. Для реализации этого закона были предложены особые приборы, названные ксилометрами. На отмеченных ксилометрах отсчеты уровня воды по отградуированной шкале берутся до и после погружения тела в воду. Разность этих объемов дает кубатуру измеряемого предмета.

Весовой способ основан на соотношении между массой тела, его плотностью и объемом: V=m/p. Весовой способ учета на практике применяется при невозможности определения объема древесины стереометрическими методами (перевозка дров в железнодорожных вагонах, отпуск саксауловых дров и т.п.). В этом случае плотность древесины устанавливают по ГОСТу..

20)Определение процента текущего прироста объема растущих деревьев.

На растущих деревьях он определяется приближенными способами, с использованием закономерных соотношений между величинами приростов различных таксационных показателей, а также связей между приростом деревьев и природными факторами, влияющими на рост деревьев.

Соотношение между процентами прироста объема и составляющих

его компонентов в формуле Vств = g1,3 ∙h∙f .

Представляет практический интерес соотношение между процентами прироста d1,3 и Vств, вытекающее из формулы PV = e∙Pd. Как показали исследования, величина коэффициента e меняется в широких пределах

– от 1,7 до 6,4 – и не может быть точно установлена в натуре. Анало-

гичная же картина сохраняется в связях Pg и PV.

Следовательно, по величине процентов прироста d1,3 и g1,3 стволов

нельзя уверенно судить о размерах PV даже в пределах одного и того же древостоя.

Существующие приближенные способы определения процента прироста объема стволов по объему основаны на ряде допущений, не всегда обоснованных и достаточно объективных. Рассмотрим наиболее известные из них.

1. При отсутствии роста дерева в высоту и неизменяемости видового числа формула:

В литературе она известна как формула Бреймана. Однако такое выражение процента прироста объема стволов применимо лишь к старым деревьям. Погрешности же в молодых возрастах составляют до -35…-40 %.

2.При условии неизменяемости только видового числа ствола исходное уравнение прироста приобретает вид:

В таком виде формула показывает систематическое преувеличение результатов, так как с возрастом видовое число стволов обычно уменьшается. Погрешность в проценте прироста объемов составляет

Для улучшения результатов проф. А.В. Тюрин предложил поправку к алгоритму

Уравнение пригодно для деревьев, прошедших кульминацию роста в высоту (обычно старше 50 лет).

3. При условии изменения видовых высот h∙f стволов пропорционально приростам диаметров на высоте 1,3 м формула (5.37) приобретает следующий вид:

Все три рассмотренные формулы для отдельных деревьев могут дать погрешности до ± 40…50 % и применимы лишь к средней оценке разнородной совокупности деревьев.

Широкое распространение в лесном хозяйстве получил способ Пресслера (1868) определения процента объемного прироста деревьев по их относительному диаметру. Относительный диаметр – это отношение диаметра на высоте 1,3 м без коры в настоящий момент к его текущему приросту за t-летний период:

Шнейдер (1853) предложил способ определения процента объемного прироста деревьев по числу годичных слоев в последнем сантиметре радиуса ствола на высоте 1,3 м.

Проф. М.Л. Дворецкий (1964) предложил формулу определения

процента объемного прироста срубленных стволов:

Источник

Способы определения объема ствола и его части

Правильными телами вращения, к которым в той или иной степени приближается форма ствола, являются: цилиндр, параболоид, конус и нейлоид. Цилиндр образуется прямой, параллельной его оси; параболоид ‑ выпуклой кривой; конус ‑ прямой, наклонной к его оси, нейлоид ‑ вогнутой кривой. Если ствол разрезать по сердцевине вертикальной плоскостью, то получится фигура, ограниченная кривой, которая называется образующей ствола. Однако, эта кривая неправильная, у большинства деревьев она асимметрична оси ствола, вследствие чего поперечное сечение его, в отличие от правильных тел вращения, является неправильным кругом. Кроме того, эта кривая является сложной, она представляет собой сочетание разных кривых: в нижней части ствола она вогнута по отношению к его оси, в средней части ‑ ближе к прямой, параллельной оси, в верхней половине образующая представляет собой выпуклую кривую, а в самой верхней части ‑ почти прямую, наклонную к оси.

Сделав сечение на границе переходов одной части образующей ствола в другую, получим фигуры, которые по своей форме приближаются к правильным телам вращения: в нижней части ‑ к усеченному нейлоиду, в средней ‑ к цилиндру, выше половины высоты ствола ‑ к усеченному параболоиду и в самой верхней части ‑ к конусу.

Следовательно, ствол не является правильным стереометрическим телом, и его только условно можно рассматривать как тело вращения вокруг оси. В практике лесной таксации применяют формулу объема целого ствола или его части по их длине и площади сечения на середине ствола или его части. Для вычисления объема по такой формуле допускают, что ствол является параболоидом вращения и используют известную формулу параболоида:

В таком виде эту формулу применять для определения объема ствола нецелесообразно, так как нижнее сечение ствола обычно имеет корневые наплывы и утолщения, поэтому используют другую формулу объема параболоида. Известно, что у обыкновенного параболоида площадь сечения прямо пропорциональна высоте. Следовательно, сделав сечение на половине высоты параболоида (рис. 4), можно написать следующую пропорцию:

где γ ‑ площадь сечения параболоида на половине его высоты.

Отсюда g_o = 2, т.е. площадь сечения основания параболоида в 2 раза больше площади сечения на половине высоты. Заменив в формуле площадь основания этим выражением, получим:

Следовательно, объем параболоида равен объему цилиндра, высота которого равна высоте параболоида, а площадь основания соответствует площади сечения на середине высоты параболоида. Эта формула в лесной таксации известна под названием простой формулы срединного сечения. Ее применяют для определения объемов ствола без вершины и отрезков ствола разной длины.

Рис. 4. Параболоид с сечением на середине

В практике таксации лесного хозяйства существуют физические способы определения объема древесины. Эти формулы основаны на использовании следующих законов физики:

— тело, погруженное в воду, вытесняет количество воды, объем которого равен объему погруженного тела;

— объем тела, состоящего их однородного вещества, прямо пропорционален его весу.

Для определения объема древесины по первому закону сконструированы особые приборы ‑ ксилометры. Они бывают с переменным и постоянным уровнем воды (рис.5).

Ксилометр с переменным уровнем воды работает по принципу сообщающихся сосудов. Это сосуд цилиндрической формы диаметром 50 ‑ 70 см и высотой около 1,5 м. В нижней части цилиндра имеется кран для сливания воды. На высоте 40 ‑ 50 см от основания в боковую стенку вделана коленчатая стеклянная трубка с открытыми концами. К трубке прикреплена шкала с делениями в 0.5 дм3; иногда шкала снабжена кониусом.

Рис. 5. Ксилометры:

а ‑ c переменным уровнем воды;

б ‑ c постоянным уровнем воды

Объем древесины ксилометром с переменным уровнем определяют следующим образом. В цилиндр наливают столько воды, чтобы в нее можно было погрузить образец древесины, объем которого желают определить. После того, как уровень воды в цилиндре установится, делают отсчет по шкале. Затем погружают в воду образец и делают отсчет по шкале. Разность двух отсчетов даст объем внутренней воды. Так как древесина, особенно сухая, способна впитывать воду, то часть воды при измерении не будет учтена, поэтому после первого отсчета образец вынимают из воды, дают воде полностью с него стечь.

Ксилометр с постоянным уровнем представляет собой сосуд из толстой жести (в лесу вместо такого цилиндра можно использовать обыкновенную кадку). В верхнюю часть цилиндра вделан кран. В цилиндр наливают воду выше уровня крана, и после того, как уровень воды установится, открывают кран, спускают лишнюю воду, кран закрывают. Затем образец древесины взвешивают и погружают в воду. После того, как уровень воды установится, под кран подставляют сосуд и открывают кран. Объем вытесненной воды измеряют или взвешивают. Образец вынимают и после того, как вода полностью стечет с него, снова взвешивают: разность между вторым и первым весом образца покажет количество воды, которое не вытеснилось образцом, а впиталось им. Эту разницу прибавляют к полученному объему вытесненной воды и получают объем образца.

Ксилометрический способ применяют при научно-исследовательских работах, в лабораториях и при определении объемов сучьев, корней, наплывов.

Источник

7) Физические способы определение объема ствола.

К физическим способам определения объема ствола относятся ксилометрические и весовые.

Ксилометрические способы базируются на одном из законов Архимеда, согласно которому тело, погруженное в воду, вытесняет равновеликий ее объем. Для реализации этого закона были предложены особые приборы, названные ксилометрами. На отмеченных ксилометрах отсчеты уровня воды по отградуированной шкале берутся до и после погружения тела в воду. Разность этих объемов дает кубатуру измеряемого предмета.

Весовой способ основан на соотношении между массой тела, его плотностью и объемом: V=m/p. Весовой способ учета на практике применяется при невозможности определения объема древесины стереометрическими методами (перевозка дров в железнодорожных вагонах, отпуск саксауловых дров и т.п.). В этом случае плотность древесины устанавливают по ГОСТу..

20)Определение процента текущего прироста объема растущих деревьев.

На растущих деревьях он определяется приближенными способами, с использованием закономерных соотношений между величинами приростов различных таксационных показателей, а также связей между приростом деревьев и природными факторами, влияющими на рост деревьев.

Соотношение между процентами прироста объема и составляющих

его компонентов в формуле Vств = g1,3 ∙h∙f .

Представляет практический интерес соотношение между процентами прироста d1,3 и Vств, вытекающее из формулы PV = e∙Pd. Как показали исследования, величина коэффициента e меняется в широких пределах

– от 1,7 до 6,4 – и не может быть точно установлена в натуре. Анало-

гичная же картина сохраняется в связях Pg и PV.

Следовательно, по величине процентов прироста d1,3 и g1,3 стволов

нельзя уверенно судить о размерах PV даже в пределах одного и того же древостоя.

Существующие приближенные способы определения процента прироста объема стволов по объему основаны на ряде допущений, не всегда обоснованных и достаточно объективных. Рассмотрим наиболее известные из них.

1. При отсутствии роста дерева в высоту и неизменяемости видового числа формула:

В литературе она известна как формула Бреймана. Однако такое выражение процента прироста объема стволов применимо лишь к старым деревьям. Погрешности же в молодых возрастах составляют до -35…-40 %.

2.При условии неизменяемости только видового числа ствола исходное уравнение прироста приобретает вид:

В таком виде формула показывает систематическое преувеличение результатов, так как с возрастом видовое число стволов обычно уменьшается. Погрешность в проценте прироста объемов составляет

Для улучшения результатов проф. А.В. Тюрин предложил поправку к алгоритму

Уравнение пригодно для деревьев, прошедших кульминацию роста в высоту (обычно старше 50 лет).

3. При условии изменения видовых высот h∙f стволов пропорционально приростам диаметров на высоте 1,3 м формула (5.37) приобретает следующий вид:

Все три рассмотренные формулы для отдельных деревьев могут дать погрешности до ± 40…50 % и применимы лишь к средней оценке разнородной совокупности деревьев.

Широкое распространение в лесном хозяйстве получил способ Пресслера (1868) определения процента объемного прироста деревьев по их относительному диаметру. Относительный диаметр – это отношение диаметра на высоте 1,3 м без коры в настоящий момент к его текущему приросту за t-летний период:

Шнейдер (1853) предложил способ определения процента объемного прироста деревьев по числу годичных слоев в последнем сантиметре радиуса ствола на высоте 1,3 м.

Проф. М.Л. Дворецкий (1964) предложил формулу определения

процента объемного прироста срубленных стволов:

Источник

51. Физические и математические способы определения объема стволов. Приближенные способы определения объема растущих деревьев.

Объем ствола срубленного дерева и его части можно определить физич. и математ. методами.

физич.методы – Ксилометрический (основан на законе Архимеда, по объёму вытесненной жидкости, с постоянным и переменным уровнем) и весовой (при нем V древесины опр-ся делением ее массы на плотность, которая зависит от породы и влажности). Используют гидростатические весы – вес в воздухе и вес в воде.

Математич.способ основаны на стереометрии. Основные объемообразующ. Показатели (Д,h и формы ствола) зависят от множества факторов (порода, А, усл.роста). Исходя из того, что ствол правильное тело вращения формулы для исчисления не сложны. Поэтому при определении объема древесного ствола его форму нередко сравнивают с правильными телами вращения, формулы которых уже известны: цилиндра (V=g₀*h) , конусом(V=g₀*h/3) , параболоидом (V=g₀*h/2) , и нейлоидом (V=g₀*h/4). Сделав сечение примерно на границе перехода одной части образующей в другую, получим фигуры: в нижней части ствола усеченный нейлоид, в средней – цилиндры, выше половины высоты – усеченный параболоид, вершинка –конусу.

Определение объема ствола растущего дерева вычисляют по формуле V_c=g_1,3*h*f. Для этой формулы площадь сечения определяют по измеренному диаметру на высоте груди, а видовое число берут из таблицы видовых чисел.

Способ Денцена V_s=d 2 _1,3/1000. Для определения – измеряют диаметр на высоте груди в целых сантиметрах, возводят его в квадрат, отделяют три десятичных знака справа и получают объем в кубометрах.

52. Классификация лесоматериалов и методы их таксации (в плотной и складочной мерах).

Сортименты – виды лесной продукции.

1.деловые – используется в круглом виде и используется для дальнейшей переработки.

2.дровяные – используется для отопления, углежжения, сухой перегонки. Таксация дров, учет в поленницах V_скл=a*l*h, V_пл=Vскл*Кт

Деловые сортименты делятся на: обработанные и круглые.

Лесоматериалы по способу получении и характеру обработки делятся на:

круглые л/м сохранившие форму боковой поверхности ствола (пиловочные и строительные бревна, руд.стойка, балансы. Из лиственных фанерный и спичечный кряж). Определение объема в плотной и складочной мере. Объем по формуле срединного сечения, существуют таблицы по D, L → V/ На практике определяется по табл. На основании длины и диаметра в верхнем отрезе, составленные для среднего сбега 1см на 1п.м.

дрова в круглом или колотом виде

пиломатериалы, полученные продольной распиловкой (пластина, четвертина, брусья, брусок, шпала, доска, горбыль, паркет)

Брусья – 2-х, 3-х, 4-х кантные по количеству пропиленных сторон. Больше 10см размеры.

л/м из корневых и прикорневых частей (осмол, болванки)

л/м из коры древ. И куст. пород

Объем хлыстов – производят перечет хлыстов по градациям толщины на 1,3м от комля, затем для 15-20 хлыстов находим, на основе вспомогательной таблице определяем разряд высот, из таблицы объема хлыстов соот. разряда выписываем объем одного хлыста для каждой категории толщины и находим хлыст + объем хлыста штабеля.

Учет круглого леса в склад.мере. V_шт=l*h*a.

Тут вы можете оставить комментарий к выбранному абзацу или сообщить об ошибке.

Источник