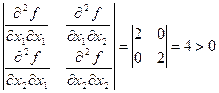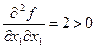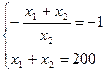Некоторые задачи оптимизации в экономике
Трейдинг криптовалют на полном автомате по криптосигналам. Сигналы из первых рук от мощного торгового робота и команды из реальных профессиональных трейдеров с опытом трейдинга более 7 лет. Удобная система мгновенных уведомлений о новых сигналах в Телеграмм. Сопровождение сделок и индивидуальная помощь каждому. Сигналы просты для понимания как для начинающих, так и для опытных трейдеров. Акция. Посетителям нашего сайта первый месяц абсолютно бесплатно .
Проиллюстрируем данный метод на конкретной задаче.
Фирма реализует автомобили двумя способами: через розничную и оптовую торговлю. При реализации х1 автомобилей в розницу расходы на реализацию составляют (4 х1+х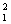
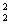
) у. е., а при продаже х2 автомобилей оптом – х
у. е. Н
айти оптимальный способ реализации автомобилей, минимизирующий суммарные расходы, если общее число, предназначенных для продажи автомобилей составляет 200шт.
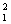
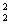
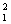
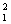
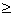
Решение: Составим функцию L(х1,х2)=4х1+х+х и будем находить её минимум. Т.к. для продажи предназначено 200 автомобилей, то х1+х2=200. Разрешим данной уравнение относительно переменной х2: х2=200-х1. Подставим полученное выражение в функцию L, получим L=4 х1+ х+ (200- х1)2=2х—396 х1+40000, х1
0.
Найдём экстремум данной функции.
L
=4 х1-396.
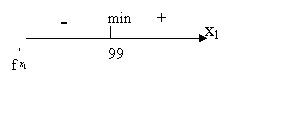
Приравняв её к нулю, получим х1=99.
Ответ: оптимальный способ реализации автомобилей – это 99 автомобилей в розницу и 101 автомобиль оптом (х2=200-99). Расходы составят 20398 р.
В экономических задачах, в которых отыскивается оптимум функции f =(x1,x2, …,хn), где n 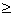2, полагают, что найденное единственное решение, удовлетворяющее необходимому условию экстремума, является оптимальным.
4. Задача потребительского выбора.
1) Функция полезности. Бюджетное ограничение. Формулировка задачи потребительского выбора.
Будем считать, что потребитель располагает доходом Q, который он полностью тратит на приобретение благ (продуктов) Учитывая структуру цен, доход и собственные предпочтения, потребитель приобретает определённое количество благ, и математическая модель такого его поведения называется моделью потребительского выбора.
В некоторых задачах выделяют один продукт, а вторым считают все остальные. Поэтому сначала рассмотрим модель с двумя видами продуктов. Потребительский набор – это вектор (x1,x2), координата x1 которого равна количеству единиц первого продукта, а координата x2 равна количеству единиц второго продукта.
Выбор потребителя характеризуется отношением предпочтения, суть которого состоит в следующем. Считается, что потребитель про каждые два набора может сказать, что либо один из них более желателен, чем другой, либо потребитель не видит между ними разницы. Отношение предпочтения транзитивно, т.е. если набор А=(а1,а2) предпочтительнее набора B=(b1,b2), а набор B=(b1,b2) предпочтительнее набора С=(с1,с2), то набор А=(а1,а2) предпочтительнее набора С=(с1,с2).
На множестве потребительских наборов (x1,x2) определена функция u(x1,x2) (называемая функцией полезности потребителя), значение u(x1,x2) которой на потребительском наборе (x1,x2)равно потребительской оценке индивидуума для этого набора. Потребительскую оценку u(x1,x2) набора (x1,x2) принято называть уровнем (или степенью) удовлетворения потребительского индивидуума, если он приобретает или потребляет данный набор (x1,x2). Каждый потребитель имеет, вообще говоря, свою функцию полезности. Если набор А 
предпочтительнее набора В, то u(А)>u(В).
Функция полезности удовлетворяет следующим свойствам:
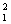
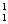
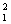
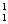
1. Возрастание потребления одного продукта при постоянном потреблении другого продукта ведёт к росту потребительской оценки, т.е. если x>x
, то u(x,x2)> u(x,x2);
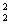
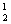
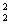
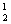
если x>x
, то u(x1, x)> u(x1, x).
Иначе говоря, u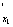
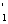
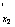
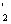
(x1,x2)=u
>0, u
(x1,x2)=u
>0.
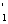
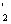
Первые частные производные u и u называются предельными полезностями первого и второго продуктов соответственно.
2. Предельная полезность каждого продукта уменьшается, если объём его потребления растёт (закон убывания предельной полезности). Из свойства второй производной следует, что u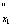
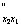
(x1,x2) 0, u
(x1,x2)=u21>0.
Линия, соединяющая потребительские наборы (x1,x2), имеющие один и тот же уровень удовлетворения потребностей называется линией безразличия. Линия безразличия есть не что иное, как линия уровня функции полезности. Множество линий безразличия называется картой линий безразличия. Линии безразличия, соответствующие разным уровням удовлетворения потребностей не пересекаются и не касаются. Чем выше и правее расположена линия безразличия, тем большему уровню удовлетворения потребностей она соответствует. Условия 1-3 означают, что линия безразличия убывает и является выпуклой вниз.
Задача потребительского выбора заключается в выборе такого потребительского набора (х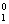
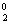
, х
), который максимизирует его функцию полезности при заданном бюджетном ограничении.
Бюджетное ограничение означает, что денежные расходы на продукты не могут превышать денежного дохода, т.е. p1x1+p2x2≤Q, где p1 и p2 – рыночные цены, а Q – доход потребителя, который он готов потратить на приобретение первого и второго продуктов. Величины p1, p2 и Q заданы.
Источник
Пример 4.4.1
Расчет экономико-математической модели при нелинейных затратах на производство
Рассмотрим применение изученных методов на примере решения задачи оптимальной реализации продукции.
Фирма реализует автомобили двумя способами: через магазин и через торговых агентов. При реализации 
автомобилей через магазин расходы на реализацию составляют 
усл. ед., а при продаже 
автомобилей через торговых агентов расходы составляют 
усл. ед. Найти оптимальный способ реализации автомобилей, минимизирующий суммарные расходы, если общее число предназначенных для продажи автомобилей составляет 200 штук.
Составим математическую модель задачи.
Целью является минимизация суммарных расходов
.
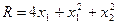
Управляющие переменные – это число автомобилей, реализуемых первым и вторым способом: и соответственно (200 штук). Окончательно математическая модель имеет следующий вид:
.
.
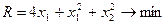
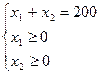
Для ее расчета применим метод множителей Лагранжа. Функция Лагранжа имеет вид
.
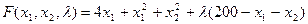
Найдем частные производные функции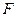 
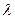
по , и 
и приравняем их к нулю.
Получим следующую систему уравнений:
.
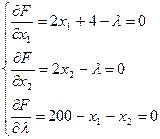
Решая систему, найдем
=99, =101, =202, 
=20398.
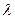
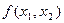
Определитель, составленный из вторых частных производных функций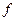 
по , , имеет вид
Следовательно, по теореме о достаточном условии существования условного экстремума функция 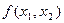в точке =99, =101 действительно имеет экстремум.
следовательно в этой точке функция 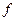имеет условный минимум.
Таким образом, для получения минимальных расходов, нужно реализовать 99 автомобилей через магазин и 101 автомобиль через торговых агентов. При этом расходы на реализацию составят 20398 усл. ед.
Данную задачу можно было решить и графическим методом (рис. 4.4.1).
Рис. 4.4.1
Областью допустимых решений задачи является отрезок АВ, линиями уровня функции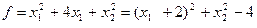 
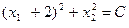
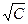
являются концентрические окружности 
с центром в точке =-2, =0 и радиусом 
.
Из рисунка видно, что минимальное значение функции, принадлежащее области допустимых решений, достигается в точке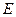 
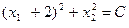
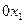
, в которой совпадают угловой коэффициент прямой =200-и касательной к окружности к оси 
.
Продифференцировав последнее уравнение по , получим
,
.
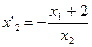
Приравняем последнее выражение к угловому коэффициенту прямой и добавим к этому уравнению уравнение прямой, которой принадлежит точка Е.
Решив последнюю систему, найдем оптимальные значения: =99, =101, =20398.
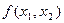
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Источник
