Фаза распределения способы распределения

Секреты VSA: Фазы накопления и распределения

Часть трейдеров никогда не задумывалось о том, как же образуются цены на финансовом рынке? Сегодня мы поговорим о спросе и предложении – тех самых причинах, которые влияют на динамичное образование цены.

Статью подготовил трейдер-аналитик Pro-TS Александр Ларин.

Как правило, малое количество предложений формирует динамическую амплитуду цены. Чем это все заканчивается? Происходит резкое повышение цены, в результате которого формируется новое предложение на рынке. Это все происходит вплоть до момента, когда цена устроит обе стороны: и продавца, и покупателя. Далее происходит движение цены уже в поиске поддержки для покупателя.

Что такое боковое движение цены? Так называется равновесие, когда обе стороны добились желаемой цены. Если мы видим, что равновесие нарушается, стоит начинать говорить об отсутствии спроса или предложения. Это характеризуется пробоем поддержки или сопротивления, цена снова начинает свое движение, чтобы стать благоприятной для обоих сторон.

Движением цены же называют исходный результат непостоянства спроса и предложения. Для того, чтобы сделать торговлю наименее рискованной и наиболее прибыльной, трейдеру необходимо скорее понять, чего же ожидают продавцы и покупатели.

Объемом в данном случае является именно то звено, которое связывает трейдера и колеблющиеся спрос и предложение. Через него трейдер видит активность продавцов и покупателей. Каким образом это происходит? Объем, естественно, постоянно изменяется, а это, в свою очередь, и позволяет оценивать потенциал спроса и предложения.

Для того, чтобы проводить анализ объема непосредственно на графике, можно использовать различные индикаторы, предназначенные для этой процедуры.

ЧТО ТАКОЕ VSA?

Volume Spread Analysis (сокращенно VSA) предназначен для определения уровня интереса участников рынка к цене, которая на данный момент присуща инструменту.

В сфере VSA существует такое понятие, как ненормальное поведение объема. Это один из факторов, который позволяет трейдеру анализировать уровень интереса инвесторов к данному торговому инструменту. Однако, существует некоторая проблема: одинаковый показатель объема может вызвать абсолютно разное поведение цен. Может происходить как боковое движение цены, так и вверх, и вниз.

Возникает логичный вопрос, каким же образом все-таки правильно используется изменение объема для определения направления цены? В этом нам помогает спред, являющийся сформированным ценовым диапазоном.

Одним из важных моментов является закрытия баров. Важно наблюдать на цену закрытия предыдущего и текущего, чтобы получить более точные показатели. Последняя цена указывает трейдеру на направление работы данного объема. Активность покупателей и продавцов характеризуется ценой закрытия баров.

Возьмем часовой график. Бар на этом графике, соответственно, образуется за час. Например, у нас был значительный прирост к объему, цена закрытия у нас оказалась ниже середины бара, а предшествующие бары показали нам на балансе положительную отметку. Цена шла вверх.

О чем это все говорит? Если рассматривать данную ситуацию совместно со спредом, то мы увидим, что сила покупателей оказалась слишком слаба для того, чтобы цена выросла. Предложение, как можно заметить, поспособствовало закрытию цены ниже середины спреда. Это может говорить о том, что вскоре образуется изменение направления тренда.

Спред и объемы помогут трейдеру в прогнозировании будущего состояния рынка, так как они ориентируются в динамике поведения рынка.

Стоит отметить, что опытные участники рынка не смогут управлять ценой при помощи контроля поведения. И на это никак не влияет размер их депозита. Однако, они постоянно будут применять другие различные способы получения прибыли на других игроках.

СЛАБЫЕ РЫНКА ПРОТИВ СИЛЬНЫХ

На рынке присутствует правило естественно отбора – выигрывает сильнейший. Сильные игроки постоянно разыскивают наиболее слабые места в биржевой толпе. Если они их все-таки находят, они начинают использовать различные манипуляции, получая, соответственно, с этого прибыль.

Стоит запомнить простой принцип: хочешь выжить – не будь в толпе слабых. Постоянно нужно работать так, как сильный игрок. Это важно, если Вы хотите получать прибыль, а не терять депозит. Ведь, если трейдер находится в толпе слабых, он автоматически предоставляет возможность сильному игроку забрать свой депозит.

Однако, спекулянты постоянно переходят на сторону слабых. Почему? Они просто-напросто бояться признавать свои ошибки. Они скрывают свою халатную торговлю за слабых игроков, перенося всю ответственность на них.

«БЫЧИЙ» РЫНОК И «МЕДВЕЖИЙ»: ФОРМИРОВАНИЕ

Переход активов от слабых игроков к сильным определяет будущее направление цены. Для того, чтобы осознать, как это все происходит, необходимо научиться проводить анализ спроса и предложения.

Примеры манипуляций:

1. Как вызвать панику у слабых игроков? Нужно лишь дождаться плохих новостей. В такие моменты поведение большинства очень предсказуемо: падение рынка означает массовые продажи, во время которых достаточно сильно вырастает предложение. А теперь попробуйте ответить на следующие вопросы: «Какой спрос сможет поглотить текущие объемы? Кто все-таки находится на противоположной стороне сделки?».
2. Большинство неопытных участников рынка часто пропускают формирование «бычьего» рынка. Соответственно, у них срабатывает инстинкт жадности, однако, уже поздно. Они нервничают, думают, что тенденция проходит мимо. Начинается массовая скупка торгового инструмента. Зачастую это происходит на экстремуме тренда. Задумайтесь, а кому выгодно находиться с противоположной стороны, распродавая активы?

Вы должны понять, что настоящая слабость рынка образуется только в росте. А сила, соответственно, в падении.

ПРИМЕРЫ НАКОПЛЕНИЯ И РАСПРЕДЕЛЕНИЯ

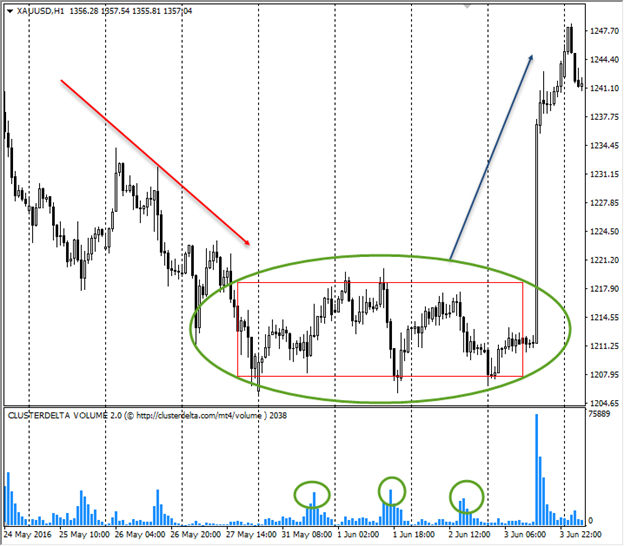
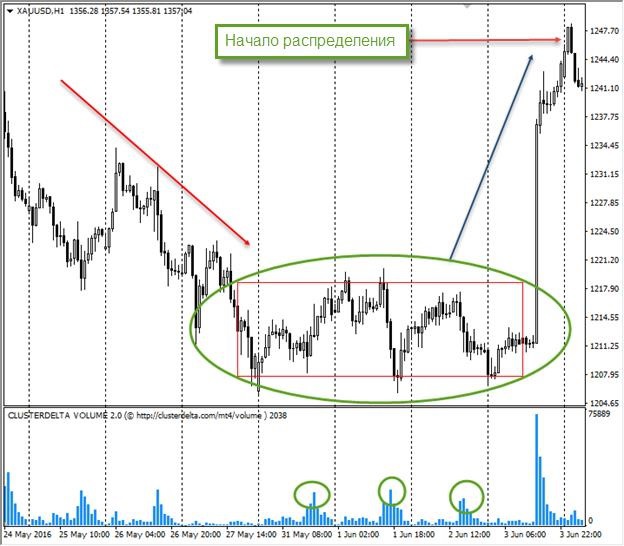
Но как все вышеописанное отображается на графике? Двумя фазами – накопления и распределения. Данные фазы идут последовательно друг за другом. На картинке приведены две фазы:

Мы каждый день видим на графике изменение сил рынка. На картинке хорошо видно боковое движение, в котором накапливаются объемы. Другими словами, на изображении представлена зона накопления.

Далее мы видим распределение объемов – зону распределения.

НАКОПЛЕНИЕ И РАСПРЕДЕЛЕНИЕ АКТИВОВ КРУПНЫМИ ИГРОКАМИ

Закон спроса и предложения можно применять к любому временному интервалу, торговой площадке и инструменты. Единственное, что изменяется – отображение крупных игроков. Они меняется от одного графика к другому. Таким образом мы видим, как они маскируют действия.

Если мы видим, что инвестиционная компания набирает позиции в процессе накопления, — это означает удержание роста цены. Таким образом мы видим, как они маскируют предложение.

Набор позиций крупными игроками осуществляется при помощи установки лимитных ордеров. Таким образом образовываются уровни поддержки/сопротивления, а также происходит порционное накопление объемов в различных зонах.

Распределение способствует передаче накопленных объемов слабым участникам. Стоит учитывать, что сама передача происходит наиболее незаметно, нежели накопление. Как итог, толпа скупает и продает все, однако, делает это с запозданием, из-за чего слабые игроки теряют свои денежные средства.

Именно поэтому я и хочу рассказать Вам про VSA-анализ, который помогает трейдеру исправить сложившуюся ситуацию. Он поспособствует скорейшему пониманию того, что же делают крупные игроки, а также сделает рынок еще более прогнозируемым.

Хотите узнать еще больше о VSA-анализе? Тогда посмотрите трансляцию вебинара, которую мы провели вместе с моим коллегой, ведущим трейдером-аналитиком Андреем Миклушевским на YouTube-канале Академии Форекса! На вебинаре мы рассказали про метод торговли VSA, который поможет Вам отследить действия крупных игроков, т.е крупные деньги на рынке Forex. Посмотрев вебинар, Вы узнаете, как объем влияет на ценовое движение и как извлечь из этого прибыль.

Источник

Типичные распределения вероятности: шпаргалка data scientist-а

У data scientist-ов сотни распределений вероятности на любой вкус. С чего начать?

Data science, чем бы она там не была – та ещё штука. От какого-нибудь гуру на ваших сходках или хакатонах можно услышать:«Data scientist разбирается в статистике лучше, чем любой программист». Прикладные математики так мстят за то, что статистика уже не так на слуху, как в золотые 20е. У них даже по этому поводу есть своя несмешная диаграмма Венна. И вот, значит, внезапно вы, программист, оказываетесь совершенно не у дел в беседе о доверительных интервалах, вместо того, чтобы привычно ворчать на аналитиков, которые никогда не слышали о проекте Apache Bikeshed, чтобы распределённо форматировать комментарии. Для такой ситуации, чтобы быть в струе и снова стать душой компании – вам нужен экспресс-курс по статистике. Может, не достаточно глубокий, чтобы вы всё понимали, но вполне достаточный, чтобы так могло показаться на первый взгляд.

Вероятностные распределения – это основа статистики, так же как структуры данных – основа computer science. Если хотите говорить языком data scientist-а – надо начинать с их изучения. В принципе можно, если повезёт, делать простые анализы, используя R или scikit-learn вообще без понимания распределений, так же как можно написать программу на Java без понимания хэшфункций. Но рано или поздно это закончится слезами, ошибками, ложными результатами или — гораздо хуже – охами и выпученными глазами от старших статистиков.

Существуют сотни различных распределений, некоторые из которых на слух звучат как чудовища средневековых легенд, типа Muth или Lomax. Тем не менее, на практике более-менее часто используются около 15. Каковы они, и какие умные фразы о них требуется запомнить?

Итак, что такое распределение вероятности?

Всё время что-то происходит: кидаются кубики, идёт дождь, подъезжают автобусы. После того, как это что-то произошло, можно быть уверенным в некотором исходе: кубики выпали на 3 и 4, выпало 2.5 см дождя, автобус подъехал через 3 минуты. Но до этого момента мы можем говорить только о том, насколько каждый исход возможен. Распределения вероятности описывают то, как мы видим вероятность каждого исхода, что, зачастую, гораздо интереснее, чем знать только один, наиболее возможный, исход. Распределения бывают разных форм, но строго одного размера: сумма всех вероятностей в распределении — всегда 1.

Например, подбрасывание правильной монетки имеет два исхода: она упадёт либо орлом, либо решкой (предполагая, что она не приземлится на ребро и её не стащит в воздухе чайка). Перед броском мы верим, что с шансом 1 к 2 или с вероятностью 0.5 она упадёт орлом. Точно так же, как и решкой. Это распределение вероятности двух исходов броска, и, если вы внимательно прочитали это предложение, то вы уже поняли распределение Бернулли.

Несмотря на экзотические названия, распространённые распределения связаны друг с другом достаточно интуитивными и интересными способами, позволяющими легко их вспоминать и уверенно о них рассуждать. Некоторые естественно следуют, например, из распределения Бернулли. Время показать карту этих связей.

Каждое распределение иллюстрируется примером её функции плотности распределения (ФПР). Эта статья только о тех распределениях, у которых исходы – одиночные числа. Поэтому, горизонтальная ось каждого графика – набор возможных чисел-исходов. Вертикальная – вероятность каждого исхода. Некоторые распределения дискретны — у них исходы должны быть целыми числами, типа 0 или 5. Таковые обозначаются редкими линиями, по одной на каждый исход, с высотой, соответствующей вероятности данного исхода. Некоторые – непрерывны, у них исходы могут принять любое численное значение, типа -1.32 или 0.005. Эти показаны плотными кривыми с областями под секциями кривой, которые дают вероятности. Сумма высот линий и областей под кривыми — всегда 1.

Распечатайте, отрежьте по пунктирной линии и носите с собой в кошельке. Это — ваш путеводитель в стране распределений и их родственников.

Бернулли и равномерное

Вы уже встретились с распределением Бернулли выше, с двумя исходами – орлом или решкой. Представьте его теперь как распределение над 0 и 1, 0 – орёл, 1 – решка. Как уже понятно, оба исхода равновероятны, и это отражено на диаграмме. ФПР Бернулли содержит две линии одинаковой высоты, представляющие 2 равновероятных исхода: 0 и 1 соответственно.

Распределение Бернулли может представлять и неравновероятные исходы, типа броска неправильной монетки. Тогда вероятность орла будет не 0.5, а какая-то другая величина p, а вероятность решки – 1-p. Как и многие другие распределения, это на самом деле целое семейство распределений, задаваемых определёнными параметрами, как p выше. Когда будете думать «Бернулли» – думайте про «бросок (возможно, неправильной) монетки».

Отсюда весьма небольшой шаг до того, чтобы представить распределение поверх нескольких равновероятных исходов: равномерное распределение, характеризуемое плоской ФПР. Представьте правильный игральный кубик. Его исходы 1-6 равновероятны. Его можно задать для любого количества исходов n, и даже в виде непрерывного распределения.

Думайте о равномерном распределении как о «правильном игральном кубике».

Биномиальное и гипергеометрическое

Биномиальное распределение можно представить как сумму исходов тех вещей, которые следуют распределению Бернулли.

Киньте честную монету два раза – сколько раз будет орёл? Это число, подчиняющееся биномиальному распределению. Его параметры – n, число испытаний, и p – вероятность «успеха» (в нашем случае – орла или 1). Каждый бросок – распределённый по Бернулли исход, или испытание. Используйте биномиальное распределение, когда считаете количество успехов в вещах типа броска монеты, где каждый бросок не зависит от других и имеет одинаковую вероятность успеха.

Или представьте урну с одинаковым количество белых и чёрных шаров. Закройте глаза, вытащите шар, запишите его цвет и верните назад. Повторите. Сколько раз вытащился чёрный шар? Это число также подчиняется биномиальному распределению.

Эту странную ситуацию мы представили, чтобы было легче понять смысл гипергеометрического распределения. Это распределение того же числа, но в ситуации если бы мы не возвращали шары обратно. Оно, безусловно, двоюродный брат биномиального распределения, но не такое же, так как вероятность успеха изменяется с каждым вытащенным шаром. Если количество шаров достаточно велико по сравнению с количеством вытаскиваний – то эти распределения практически одинаковы, так как шанс успеха изменяется с каждым вытаскиванием крайне незначительно.

Когда где-то говорят о вытаскивании шаров из урн без возврата, практически всегда безопасно ввернуть «да, гипергеометрическое распределение», потому что в жизни я ещё не встречал никого, кто реально наполнял бы урны шарами и потом вытаскивал их и возвращал, или наоборот. У меня даже знакомых нет с урнами. Ещё чаще это распределение должно всплывать при выборе значимого подмножества некоторой генеральной совокупности в качестве выборки.

Тут может быть не очень понятно, а раз туториал и экспресс-курс для новичков — надо бы разъяснить. Генеральная совокупность — есть нечто, что мы хотим статистически оценить. Для оценки мы выбираем некоторую часть (подмножество) и производим требуемую оценку на ней (тогда это подмножество называется выборкой), предполагая, что для всей совокупности оценка будет похожей. Но чтобы это было верно, часто требуются дополнительные ограничения на определение подмножества выборки (или наоборот, по известной выборке нам надо оценить, описывает ли она достаточно точно совокупность).

Практический пример — нам нужно выбрать от компании в 100 человек представителей для поездки на E3. Известно, что в ней 10 человек уже ездили в прошлом году (но никто не признаётся). Сколько минимум нужно взять, чтобы в группе с большой вероятностью оказался хотя бы один опытный товарищ? В данном случае генеральная совокупность — 100, выборка — 10, требования к выборке — хотя бы один, уже ездивший на E3.

В википедии есть менее забавный, но более практичный пример про бракованные детали в партии.

Пуассон

Что насчёт количества заказчиков, звонящих по горячей линии в техподдержку каждую минуту? Это исход, чьё распределение на первый взгляд биномиальное, если считать каждую секунду как испытание Бернулли, в течение которой заказчик либо не позвонит (0), либо позвонит (1). Но электроснабжающие организации прекрасно знают: когда выключают электричество – за секунду могут позвонить двое или даже больше сотни людей. Представить это как 60000 миллисекундных испытаний тоже не поможет – испытаний больше, вероятность звонка в миллисекунду меньше, даже если не учитывать двух и более одновременно, но, технически – это всё ещё не испытание Бернулли. Тем не менее, срабатывает логическое рассуждение с переходом к бесконечности. Пусть n стремится к бесконечности, а p – к 0, и так, чтобы np было постоянным. Это как делить на всё более малые доли времени со всё менее малой вероятностью звонка. В пределе мы получим распределение Пуассона.

Так же, как и биномиальное, распределение Пуассона – это распределение количества: количества раз того, как что-то произойдёт. Оно параметризуется не вероятностью p и количеством испытаний n, но средней интенсивностью λ, что, в аналогии с биномиальным, просто постоянное значение np. Распределение Пуассона – то, о чём надо вспоминать, когда идёт речь о подсчёте событий за определённое время при постоянной заданной интенсивности.

Когда есть что-то, типа прихода пакетов на роутер или появления покупателей в магазине или что-то, ожидающее в очереди – думайте «Пуассон».

Геометрическое и отрицательное биномиальное

Из простых испытаний Бернулли появляется другое распределение. Сколько раз монетка выпадет решкой, прежде, чем выпасть орлом? Число решек подчиняется геометрическому распределению. Как и распределение Бернулли, оно параметризуется вероятностью успешного исхода, p. Оно не параметризуется числом n, количеством бросков-испытаний, потому что число неудачных испытаний как раз и есть исход.

Если биномиальное распределение это «сколько успехов», то геометрическое это «Сколько неудач до успеха?».

Отрицательное биномиальное распределение – простое обобщение предыдущего. Это количество неудач до того, как будет r, а не 1, успехов. Поэтому оно дополнительно параметризуется этим r. Иногда его описывают как число успехов до r неудач. Но, как говорит мой лайф-коуч: «Ты сам решаешь, что есть успех, а что — неудача», так что это тоже самое, если при этом не забыть, что вероятность p тоже должна правильной вероятностью успеха или неудачи соответственно.

Если нужна будет шутка для снятия напряжения, можно упомянуть, что биномиальное и гипергеометрическое распределение – это очевидная пара, но и геометрическое и отрицательное биномиальное так же весьма похожи, после чего заявить «Ну и кто же так их все называет, а?»

Экспоненциальное и Вейбула

Снова о звонках в техподдержку: сколько пройдёт до следующего звонка? Распределение этого времени ожидания как будто бы геометрическое, потому что каждая секунда, пока никто не звонит – это как неуспех, до секунды, пока, наконец, звонок не произойдёт. Количество неудач –это как количество секунд, пока никто не звонил, и это практически время до следующего звонка, но «практически» нам недостаточно. Суть в том, что это время будет суммой целых секунд, и, таким образом, не получится посчитать ожидание внутри этой секунды до непосредственно звонка.

Ну и, как и раньше, переходим в геометрическом распределении к пределу, относительно временных долей – и вуаля. Получаем экспоненциальное распределение, которое точно описывает время до звонка. Это непрерывное распределение, первое такое у нас, потому что исход не обязательно в целых секундах. Как и распределение Пуассона, оно параметризуется интенсивностью λ.

Повторяя связь биномиального с геометрическим, Пуассоновское «сколько событий за время?» связано с экспоненциальным «сколько до события?». Если есть события, количество которых на единицу времени подчиняется распределению Пуассона, то время между ними подчиняется экспоненциальному распределению с тем же параметром λ. Это соответствие между двумя распределениями необходимо отмечать, когда обсуждается любое из них.

Экспоненциальное распределение должно приходить на ум при размышлении о «времени до события», возможно, «времени до отказа». По факту, это такая важная ситуация, что существуют более обобщённые распределения чтобы описать наработку-на-отказ, типа распределения Вейбула. В то время, как экспоненциальное распределение подходит, когда интенсивность — износа, или отказов, например – постоянна, распределение Вейбула может моделировать увеличивающуюся (или уменьшающуюся) со временем интенсивность отказов. Экспоненциальное, в общем-то, частный случай.

Думайте «Вейбул» когда разговор заходит о наработке-на-отказ.

Нормальное, логнормальное, Стьюдента и хи-квадрат

Нормальное, или гауссово, распределение, наверное, одно из важнейших. Его колоколообразная форма узнаётся сразу. Как и e, это особенно любопытная сущность, которая проявляется везде, даже из внешне самых простых источников. Возьмите набор значений, подчиняющихся одному распределению – любому! – и сложите их. Распределение их суммы подчиняется (приблизительно) нормальному распределению. Чем больше вещей суммируется – тем ближе их сумма соответствует нормальному распределению (подвох: распределение слагаемых должно быть предсказуемым, быть независимым, оно стремится только к нормальному). То, что это так, несмотря на исходное распределение – это потрясающе.

Меня удивило, что автор не пишет про необходимость сопоставимого масштаба суммируемых распределений: если одно существенно доминирует надо остальными — сходиться будет крайне плохо. И, в общем-то, абсолютная взаимная независимость необязательна, достаточна слабая зависимость.

Ну сойдёт, наверное, для вечеринок, как он написал.

Это называется «центральная предельная теорема», и надо знать, что это, почему так названо и что означает, иначе моментально засмеют.

В её разрезе, нормальное связано со всеми распределениями. Хотя, в основном, его связывают с распределениями всяких сумм. Сумма испытаний Бернулли следует биномиальному распределению и, с увеличением количества испытаний, это биномиальное распределение становится всё ближе в нормальному распределению. Аналогично и его двоюродный брат – гипергеометрическое распределение. Распределение Пуассона – предельная форма биномиального – так же приближается к нормальному с увеличением параметра интенсивности.

Исходы, которые подчиняются логнормальному распределению, дают значения, логарифм которых нормально распределён. Или по-другому: экспонента нормально распределённого значения логнормально распределена. Если суммы – нормально распределены, то запомните так же, что произведения распределены логнормально.

t-Распределение Стьюдента – это основа t-теста, который многие нестатистики изучают в других областях. Оно используется для предположений о среднем нормального распределения и так же стремится к нормальному распределению с увеличением своего параметра. Отличительная особенность t-распределения – его хвосты, которые толще, чем у нормального распределения.

Если толстохвостый анекдот недостаточно раскачал вашего соседа – переходите в довольно забавной байке про пиво. Больше 100 лет назад Гиннесс использовал статистику, чтобы улучшить свой стаут. Тогда Вильям Сили Госсет и изобрёл полностью новую статистическую теорию для улучшенного выращивания ячменя. Госсет убедил босса, что другие пивовары не поймут, как использовать его идеи, и получил разрешение на публикацию, но под псевдонимом «Стьюдент». Самое известное достижение Госсета – как раз это самое t-распределение, которое, можно сказать, названо в честь него.

Наконец, распределение хи-квадрат – распределение сумм квадратов нормально-распределенных величин. На этом распределении построен тест хи-квадрат, который сам основан на сумме квадратов разниц, которые должны быть нормально распределены.

Гамма и бета

В этом месте, если вы уже заговорили о чём-то хи-квадратном, разговор начинается всерьёз. Вы уже, возможно, говорите с настоящими статистиками, и, наверное, стоит уже откланиваться, поскольку могут всплыть вещи типа гамма-распределения. Это обобщение и экспоненциального, и хи-квадрат распределения. Как и экспоненциальное распределение, оно используется для сложных моделей времен ожидания. Например, гамма-распределение появляется, когда моделируется время до следующих n событий. Оно появляется в машинном обучении как «сопряжённое априорное распределение» к парочке других распределений.

Не вступайте в разговор об этих сопряжённых распределениях, но если всё-таки придётся, не забудьте сказать о бета-распределении, потому что оно сопряжённое априорное к большинству упомянутых здесь распределений. Data-scientist-ы уверены, что оно именно для этого и сделано. Упомяните об этом ненароком и идите к двери.

Начало мудрости

Распределения вероятности — это то, о чём нельзя знать слишком много. По настоящему заинтересованные могут обратиться к этой супердетализированной карте всех распределений вероятности. Надеюсь, этот шуточный путеводитель даст вам уверенность казаться «в теме» в современной технокультуре. Или, по крайней мере, способ с высокой вероятностью определить, когда надо идти на менее ботанскую вечеринку.

Шон Овен – директор Data Science в Cloudera, Лондон. До Клаудеры он основал Myrrix Ltd. (сейчас проект Oryx) для коммерционализации широкомасштабных рекомендательных систем в реальном времени на Hadoop. Он так же контрибьютор Apache Spark и соавтор O’Reilly Media’s Advanced Analytics with Spark

Источник