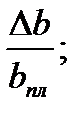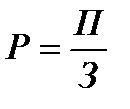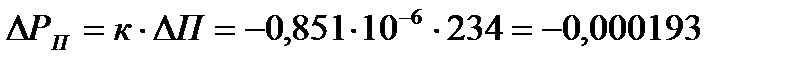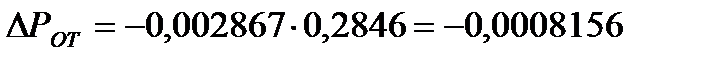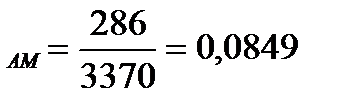Факторный анализ способом цепной подстановки или абсолютных разниц

Способ цепных подстановок. Формула. Пример в Excel. Факторный анализ

Рассмотрим достаточно популярный элемент экономического анализа — метод цепных подстановок.

Общая характеристика метода цепных подстановок

Одним из универсальных и распространенных элементов экономического анализа является метод цепных подстановок. Используют его для определения степени воздействия отдельных факторов на конкретные совокупные показатели. Он позволяет:

• объяснить, как конкретный фактор на них отражается, влияет на их изменение;
• путем расчета выяснить отклонения одних типов значений от других (фактических от нормативных).

Важно! Данный способ применяют, когда речь идет о прямой и обратно пропорциональной зависимости.

Для него характерна универсальность и сравнительная простота в расчетах. Это позволяет применять его часто и, что немаловажно, при анализе разных факторных моделей (FACTOR MODEL). Мультипликативных, кратных и т. д.

Суть метода подстановки состоит в последовательной замене значений факторов:

• базисных на отчетные;
• либо плановых на фактические.

Изначально взаимосвязанные факторы размещают определенным порядком. Сначала – количественные, те, которые выражают количество, подлежат учету. Вслед за ними – качественные, характеризуемые признаками, внутренними качествами.

Наглядный пример. Предположим, нужно выяснить влияние количества работников и производительности (результативности) труда на объем производимых хозяйственных товаров. С этой целью сначала определяют влияние количественного фактора (численности персонала), а только потом – качественного (продуктивности, производительности).

Когда качественных и количественных факторов много, руководствуются принципом «сначала наиболее общие, а затем остальные». Т. е. факторы первого порядка (определяют результат), второго порядка (воздействуют на результат) и т. д. Затем с их участием при помощи расчетов, заменяя значения, вычитая, определяют влияние факторов на изменение анализируемого совокупного показателя.

Оценка стоимости бизнеса	Финансовый анализ по МСФО	Финансовый анализ по РСБУ
Расчет NPV, IRR в Excel	Оценка акций и облигаций

Формула метода цепных подстановок

Рассмотрим стандартный вариант расчета для двух факторов, из которых построена мультипликативная модель анализируемого показателя. Основные этапы калькуляции:

1. Замена базисных значений факторов на отчетные.
2. Определение влияния двух факторов (Ф1 и Ф2) на изменение показателя П.

В формулах используется модель: П=Ф1 * Ф2, а также сокращения: б – базисные значения, о – отчетные и ус – условные. Последовательность действий:

3. Замена значений:

Пб=Ф1б * Ф2б (1)

Пус=Ф1о * Ф2б (2)

По=Ф1о * Ф2о (3)

4. Определение влияния Ф1 на изменение анализируемого показателя (Пф1):

Пф1=Пус – Пб (4)

5. Определение влияния Ф2 на изменение анализируемого показателя (Пф2):

Пф2=По – Пус (5)

6. Проверка соответствия алгебраической суммы и итогового общего показателя (Пи):

Пи = Пф1 + Пф2 (6)

На этом расчет закончен. Аналогичным путем производят замену значений плановых показателей на фактические, и, соответственно, выясняют влияние факторов на изменение анализируемого показателя.

Важно! Самостоятельно выполнить необходимые расчеты, используя метод цепных подстановок, можно при помощи онлайн калькулятора. Для этого требуется в предложенную форму внести все значения факторов влияния и кликнуть «выполнить расчет».

Алгоритм метода

Подытоживая все действия при калькуляции по формулам, приведенным выше, можно вывести некий общий алгоритм действий. Итак, влияние конкретного фактора на изменение анализируемого показателя определяют следующим путем:

1. Значение первого фактора в базисном периоде (раннем) заменяют на его значение в отчетном периоде (последующем, более позднем).
2. В итоге получают первое условное значение.
3. После замены смотрят, как изменился анализируемый показатель.
4. Для этого отнимают от условного значения показателя его базисную величину. Это и будет размер влияния 1 фактора.
5. Затем по аналогии путем замены и вычитания значений определяют влияние остальных факторов.

Важно! Условный показатель – результат замены значений. Например, условный показатель 1 – замены первого значения, условный показатель 2 – замены второго и т. д.

Итоги, на которые следует обратить особое внимание:

1. Влияние на конкретный показатель выясняют посредством вычитания. Для этого из результата второго расчета отнимают результат первого, затем, последовательно, из третьего – результат второго и так до конца.
2. Для определения влияния 2 факторов, выполняют 3 расчета, соответственно, для 3 факторов – 4 расчета и т. д.
3. Если речь идет о плановых и фактических показателях, то их замену производят тоже по приведенному выше алгоритму. Причем первый расчет всегда содержит одни плановые величины, сведения для него берут из плана предприятия. Последний расчет включает только фактические величины и данные для него берут из соответствующего отчета (за квартал, год).

Недостаток метода цепных подстановок

Минусов у этого метода не так уж и много, но при расчетах они имеют немаловажное значение. Во-первых, конечный результат (это величина влияния на совокупный показатель) напрямую зависит от последовательности подстановок. Если порядок замены значений поменять, то изменится и результат (величина влияния), причем каждого фактора. Во-вторых, если в расчетах опущен какой-то фактор, есть арифметическая ошибка, величина влияния некоторых факторов будет неточной. При этом общий итог может быть верным.

Учитывая это, следует придерживаться следующей последовательности в расчетах:

1. Установить взаимосвязь всех имеющихся факторов.
2. Разделить их на количественные и качественные.
3. Выяснить, как, в каком порядке нужно их подменять.

Важно! Нельзя произвольно менять последовательность подстановок, т. к. это приводит к отклонениям в расчетах и различиям в оценке влияния факторов. И чем больше отклонений, тем больше разница.

Это главный недостаток метода, который надо учитывать при калькуляциях. Устранить его можно при помощи математических способов анализа, но лучше, конечно, до этого не доводить.

Способ цепных подстановок. Факторный анализ

Под факторным анализом понимают многомерность метода, который применяют для комплексного исследования, выяснения степени воздействия факторов на величину итоговых показателей. Когда связь между факторами и этими показателями имеет функциональный характер, влияние факторов изучают при помощи детерминированного факторного анализа. Вот тогда-то и применяются способ цепных подстановок. Хотя, помимо него, еще используют и другие способы, например:

• относительных или абсолютных разниц;
• индексный;
• интегральный и др.

Первые два способа, а также цепная подстановка базируются на элиминировании, что подразумевает исключение, устранение влияния всех факторов на величину соответствующего показателя, помимо одного. Простыми словами, все факторы подлежат изменению не зависимо друг от друга. Сначала меняется только один, затем только два, потом только три. Но другие во время их изменений остаются неизменными. Это позволяет выяснить влияние каждого отдельно взятого фактора на рассматриваемый показатель.

Среди применяемых способов детерминированного факторного анализа самыми часто используемыми являются именно цепные подстановки. Их универсальность позволяет, как уже было сказано выше, применять его в расчетах для всех факторных моделей. Тем не менее, у них есть существенный недостаток. Факторы не зависят друг от друга, влияют только на совокупный (анализируемый) показатель и при расчетах их нужно заменять в строгой порядке, иначе результаты будут неточными.

Кстати сказать, устранить этот недостаток может интегральный способ детерминированного факторного анализа. Месторасположение факторов при калькуляции этим способом не сказывается на результате их влияния. Поэтому он выдает более точные значения при установлении степени воздействия факторов на показатель.

Пример анализа методом цепных подстановок

Цель анализа: определить влияние двух факторов (продажной стоимости товара и количества реализованного товара) на объем продаж (анализируемый показатель).

Мультипликативная факторная модель: ОП (объем продаж либо выручка)= Кпт (количество проданного товара) * Це (цена единицы товара).

Условные данные и обозначения для калькуляции:

• количество проданного товара: 1 500 шт. (согласно плану) и 2 000 шт. (по факту);
• цена 1 един. товара: 4,5 р. (согласно плану) и 5,7 р. (по факту).

1. Сначала производим замену значений факторов: ОПп = Кпт (по плану) * Це (по плану), затем ОП ус. = Кпт (по факту) * Це (по плану) и, наконец, ОПф = Кпт (по факту) * Це (по факту).
2. Затем определяем влияние 1 фактора (количества реализованного товара) на ОП путем следующего вычитания: ОПус – ОПп
3. Далее определяем влияние 2 фактора (цены 1 товара), аналогично, путем вычитания: ОПф – ОПус
4. В завершение сверяем алгебраическую сумму и итоговый показатель – результат должен быть одинаковым.

Используемые сокращения в расчетах: п – по плану, ф – фактически, ус – условно. Т. е. ОПп – плановое значение показателя, ОПф – фактическое, ОПус – условное. Калькуляция и ее результаты приведены далее в таблице.

ОП (Кпт)=9 000 – 6 750 = 2 250 р.

ОП (Це)=11 400 – 9 000 = 2 400 р.

Замена значений	Определение влияния Кпт на ОП	Определение влияния Це на ОП	Сверка алгебраической суммы и итогового показателя
ОПп=1 500 * 4,5 = 6 750 р. ОПусл.=2 000 * 4,5 =9 000 р. ОПф=2 000 * 5,7 =11 400 р.	ОП (Кпт) + ОП(Це) = 2 250 + 2 400 = 4 650 р. ОПф – Опп = 11 400 – 6 750 = 4 650 р. Результат одинаков: 4 650 р. = 4 650 р.

Подводим итоги:

1. Объем продаж (анализируемый показатель) повысился на 4 650 р.
2. Изменение показателя вызвано ростом количества реализованного товара с 1 500 шт. до 2 000 шт. (всего на 500 шт.). За счет реализации этих 500 единиц объем продаж увеличился на 2 250 р.
3. Изменение показателя вызвано также ростом продажной цены товара на 1,2 р. (5,7 р. – 4,5 р.). При этом увеличение объема продаж составило 2 400 р.

Пример решения задачи методом цепных подстановок

В 2018 г. предприятие реализовало 200 станков. Продажная цена 1 единицы на тот момент составляла 310 тыс. руб. В следующем 2019 г. было реализовано 195 станков, но уже по цене 320 тыс. руб. за каждый.

Задача: определить, какой фактор повлиял на снижение выручки и насколько, а какой – на увеличение. За основу берется базисный период (б) – 2018 г. и отчетный (о) – 2019 г.

Последовательность решения задачи:

1. Определяем размер выручки за 2018 г.: Вб = Сб (количество реализованных станков в базисном периоде) * Цб (цена 1 станка в этом же базисном периоде) = 200 ст.* 310 тыс. руб. = 62 000 тыс. руб.
2. Находим условную выручку (Ву) при изменении количества станков с 200 (в 2018 г.) до 195 (в 2019 г.): Ву = Со (количество реализованных станков в отчетном периоде) * Цб = 195 ст. * 310 тыс. руб. = 60 450 тыс. руб.
3. Определяем размер выручки за отчетный 2019 г.: Во = Со (количество реализованных станков в отчетном периоде) * Цо (цену 1 станка в отчетном периоде) = 195 ст. * 320 тыс. руб. = 62 400 тыс. руб.
4. Выясняем, как повлияло уменьшение количества реализованных станков в 2019 г. на размер выручки: Ву – Вб = 60 450 тыс. руб. – 62 000 тыс. руб. = – 1 550 тыс. руб. Получилось отрицательное значение, которое говорит о том, что из-за уменьшения числа реализованных станков выручка снизилась на 1 550 тыс. руб.
5. Выясняем, как повлиял рост цены за 1 станок на выручку в 2019 г.: Во – Ву = 62 400 тыс. руб. – 60 450 тыс. руб. = 1 950 тыс. руб. Это значит, что в результате роста продажной цены выручка возросла на 1 950 тыс. руб.
6. Разница выручки в отчетном и базисном периодах: 62 400 тыс. руб. – 62 000 тыс. руб. = 400 тыс. руб.

Резюмируем. Оптимальный вариант развития для предприятия в создавшейся ситуации – увеличение объема реализуемой продукции (станков). Для этого нужно искать новые рынки сбыта. Чем больше будет продано станков, тем, соответственно, больше будет выручка.

Источник

Факторный анализ, его приемы: цепных подстановок, абсолютных и относительных разниц, долевого участия, интегральный.

Под факторным, анализом, понимается методика комплексного и системного изучения и измерения воздействия факторов на величину результативных показателей.

В зависимости от характера исследуемых взаимосвязей различа­ют детерминированный и стохастический факторный анализ.

Детерминированный факторный анализ исследует влияние факто­ров, связь которых с результативным показателем носит функцио­нальный характер, т.е. когда величина результативного показателя может быть представлена в виде произведения, частного или алгеб­раической суммы нескольких факторов.

В детерминированном анализе выделяют следующие типы наиболее часто встречающихся факторных моделей.

1 . Аддитивные модели:

Они используются в тех случаях, когда результативный показатель представляет собой алгебраическую сумму нескольких факторных показателей.

2. Мультипликативные модели:

Этот тип моделей применяется тогда, когда результативный по­казатель представляет собой произведение нескольких факторов.

Они применяются тогда, когда результативный показатель получают делением одного факторного показателя на величину другого.

4.Смешанные (комбинированные) модели — это сочетание в различных комбинациях предыдущих моделей:

У=(а+b)/с У=а/(b+с) У=а*b/с У=(а+b) и т.д.

Стохастический анализпредставляет собой методику исследования факторов, связь которых с результативным показателем в отличие от функциональной является неполной, вероятностной (корреляционной).

В детерминированном факторном анализе используются следующие способы: цепной подстановки, индексный, абсолютных разниц, относительных разниц, пропорционального деления, интегральный, логарифмирования и др.

Первые четыре способа основываются на методе элиминирования. Элиминировать — это значит устранить, отклонить, исключить воздействие всех факторов на величину результативного показателя, кроме одного!’ Этот метод исходит из того, что все факторы изменяются независимо друг от друга: сначала изменяется один, а все другие остаются без изменения, потом изменяются два, затем три и т.д., при неизменности остальных. Это позволяет определить влияние каждого фактора на величину исследуемого показателя в отдельности.

Наиболее универсальным из них является способ цепной подстановки.Он используется для расчета влияния факторов во всех типах детерминированных факторных моделей. Этот способ позволяет определить влияние отдельных факторов на изменение величины результативного показателя путем постепенной замены базисной величины каждого факторного показателя в объеме результативного на фактическую в отчетном периоде. С этой целью определяют ряд условных величин результативного показателя, которые учитывают изменение одного, затем двух, трех и т.д. факторов, допуская, что остальные не меняются. Сравнение величины результативного показателя до и после изменения уровня определенного фактора позволяет элиминироваться от влияния всех факторов, кроме одного, и определить воздействие последнего на прирост результативного показателя.

Рассмотрим алгоритм расчета влияния факторов для мультипликативной факторной модели типа Y = а *b * с * d.

Имеются плановые и фактические значения по каждому факторному показателю.

Определяем изменение величины результативного показателя за счет каждого фактора:

Способ абсолютных разницявляется одной из модификаций элиминирования. Как и способ цепной подстановки, он применяется для расчета влияния факторов на прирост результативного показателя в детерминированном анализе, но только в мультипликативных и мультипликативно-аддитивных моделях: Y = (а-b)с и Y = а(b-с). И хотя его использование ограничено, но благодаря своей простоте он получил широкое применение в АХД. Особенно эффективно применяется этот способ в том случае, если исходные данные уже содержат абсолютные отклонения по факторным показателям.

При его использовании величина влияния факторов рассчитывается умножением абсолютного прироста исследуемого фактора на базовую (плановую) величину факторов, которые находятся справа от него, и на фактическую величину факторов, расположенных слева от него в модели.

Рассмотрим алгоритм расчета для мультипликативной факторной модели типа Y = а *b * с * d.

Имеются плановые и фактические значения по каждому факторному показателю, а также их абсолютные отклонения:

Определяем изменение величины результативного показателя за счет каждого фактора:

Как правило из приведенной схемы, расчет строится на последовательной замене плановых значений факторных показателей на их отклонения, а затем на фактический уровень этих показателей.

Способ абсолютных разниц дает те же результаты, что и способ цепной подстановки. Здесь также необходимо следить за тем, чтобы алгебраическая сумма прироста результативного показателя за счет отдельных факторов была равна общему его приросту.

Способ относительных разниц, как и предыдущий, применяется для измерения влияния факторов на прирост результативного показателя только в мультипликативных и аддитивно-мультипликативных моделях типа У = (а-b)с.

Рассмотрим методику расчета влияния факторов этим способом для мультипликативных моделей типа Y = а *b * с * d.

Изменение результативного показателя определяется следующим образом:

∆Y_a = Y_пл×

∆Y_b = (Y_пл +∆Y_a) ×

∆Y_c = (Y_пл +∆Y_a +∆Y_b ) ×

Результаты расчетов те же, что и при использовании предыдущих способов.

Способ относительных разниц удобно применять в тех случаях, когда требуется рассчитать влияние большого комплекса факторов (8-10 и более). В отличие от предыдущих способов значительно сокращается количество вычислений.

Метод пропорционального деления и долевого участия. Применяется к кратным и смешанным моделям. Согласно методу пропорционального деления рассчитывается коэффициент пропорционального деления.

, ,где DF — общее изменение результативного показателя.

Оценка влияния каждого фактора путём умножения коэффициента пропорционального деления на изменение этого показателя.

Согласно методу долевого участия определяется объём долевого участия как удельный вес изменения исследуемого факторного показателя в общем изменении всех факторов.

В кратных моделях влияние фактора, стоящего в знаменателе, по указанным методам не всегда возможно определить объективно. Указанные приёмы, как правило, в смешанных моделях применяются в сочетании.

Рассмотрим пример использования приема пропорционального деления и долевого участия.

Показатель	Предшествующий год	Отчетный год
Прибыль от реализации
Затраты на производство и сбыт продукции
в т. ч. мат. затраты
ФОТ и отчисления на соц. нужды
Амортизация ОПС
Прочие затраты

DР=- 0,003071, DЗ=3370, DП=234

Снижение рентабельности за отчётный год было обусловлено опережающим ростом затрат над ростом прибыли.

Коэффициент долевого участия для всех видов затрат:

d

d

d

d

Элиминирование – как способ детерминированного факторного анализа предполагает, что факторы, влияющие на результативный показатель, не зависят друг от друга. И это является существенным недостатком способа цепных подстановок и относительных и абсолютных разниц. Интегральный способ позволяет устранить этот недостаток. Этот способ используется в мультипликативных, кратных и смешанных моделях кратно-аддитивного вида. Результаты влияния факторов не зависят от местоположения факторов в модели, что позволяет с большей точностью рассчитать их воздействие.

Рассмотрим методику расчета мультипликативных моделей:

1). А = В *С

; или

; или

2). на примере мультипликативной модели А = В *С* D

;

;

.

Для методики расчета в кратных и смешанных моделях используются следующие рабочие формулы:

1). для кратной модели

;

2). для смешанной модели кратно-аддитивного вида

; ;

.

Использование интегрального метода не требует знания всего процесса интегрирования. Достаточно в готовые рабочие формулы подставить необходимые числовые данные и сделать не очень сложные расчеты с помощью калькулятора или компьютера в Ехсе1. При этом достигается более высокая точность расчетов.

Источник

Читайте также:  Каковы основные способы образования имен прилагательных