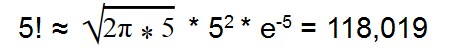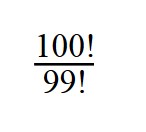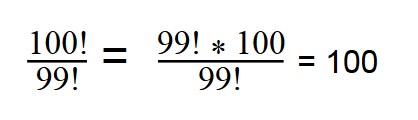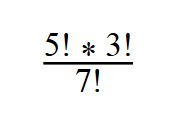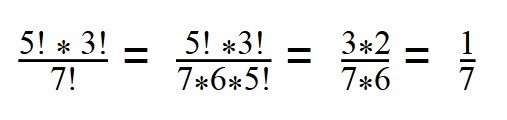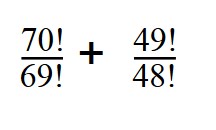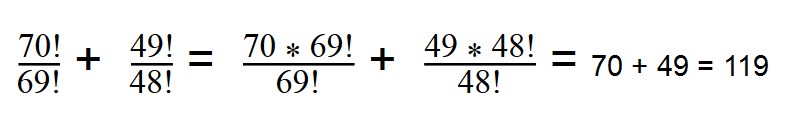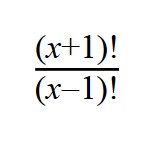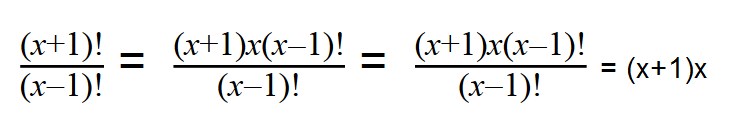Что такое факториал?
Я думаю трудно найти человека, который не знал бы, что такое факториал. Но, чёрт возьми, такая красивая математическая операция, давайте поговорим о ней снова. Тем более постарался максимально доходчиво объяснить материал даже очень далеким от математики людям. Поехали!
Кто из Вас помнит, когда столкнулся с факториалом впервые? Я, например, абсолютно уверен, что первый раз увидел значок n! на советской микро-ЭВМ Электроника МК-71. Меня поразило, в первую очередь, как с помощью этой кнопки быстро переполняется буфер и выскакивает ошибка. Потом уже, начав изучать математику, удалось поближе познакомиться с этим зверем. Начнем с определения:
Лаконично и просто.
Факториал крут тем, насколько быстро возрастает его значение, и если 5! равен всего лишь 120, то 10! — уже 3 628 800, а, например, факториал 1000000 равен 8,263931688Е+5565708. Факториал возрастает быстрее чем экспонента и степенная функция и даже чем их произведение, но, однако уступает функции n в степени n.
Короткий пример вычисления факториала
Важное уточнение: 0! = 1, что следует из определения факториала.
Самым натуральным образом понятие «факториал» возникает в комбинаторике при попытке посчитать количество перестановок элементов множества. Например, пусть множество состоит из 4 шаров разного цвета: красного, синего, желтого и зеленого. Ответьте на вопрос: сколько существует способов укладки этих шаров (разный порядок — разный способ) ?
Если взять первым красный шар, а затем найти варианты расположения остальных — получим 6 вариантов. Перебрав все 4 шара получим 24 = 1*2*3*4=4! Таким образом, количество перестановок во множестве равно факториалу количества его членов.
Во-вторых, факториал применяется при расчете количества размещений — еще одной операции из мира комбинаторики. Суть ее проста, поясним ее на всё том же примере разноцветных шаров. Ответьте на вопрос: сколько способов отдельного размещения 2 шаров из представленных 4 (разный порядок — разный способ) ?
Всего имеется 12 вариантов размещения 2 элементов из 4. То, что мы сейчас посчитали руками формализуется следующим образом через факториал:
Читается как количество размещений из n элементов по m
В-третьих, факториал присутствует в формуле количества сочетаний из n элементов по m. Сочетания отличаются от размещений тем, что если набор элементов одинаков — он не учитывается.
На рисунке обведены сочетания: как видно, их стало в 2 раза меньше. Формула вычисления количества сочетаний из n элементов по k выглядит так:
Раз уж мы разобрались с перестановками, размещениями и сочетаниями, перейдем к «имени нарицательному», страшному и пугающему: биному Ньютона. Как окажется, знание факториала и последней формулы легко позволит Вам расколоть этот «крепкий орешек».
Как ни странно, бином Ньютона это выражение (1+x)^n и его легко найти через формулу сочетаний (доказательство естественно опустим). Вот небольшой пример нахождения бинома третьей степени, который легко перепроверить перемножением.
Разобравшись с этим примером, можете спокойно спорить с друзьями и знакомыми, что без проблем вычислите бином Ньютона n-ной степени!
Некоторые интересные свойства факториала
Во многих случаев, когда не требуется точного вычисления факториала не требуется, можно воспользоваться формулой Стирлинга:
Например, реальное значение факториала 5 — это 120. По формуле Стирлинга получается так:
Строго говоря, это только первый член бесконечного ряда. С увеличением количества членом приближение будет всё точнее
Идем дальше. До этого мы условились, что в качестве подфакториальной переменной, рассматриваем только натуральные числа. А что, если бы нам захотелось вычислить факториал дробного числа? Оказывается, и такой факториал тоже существует.
Используются такие расчеты при статистическом описании нейронных сетей. Данные вычисления приближенные, чтобы точно вычислять значение таких факториалов, используется Гамма-функция. Но это уже совсем другая история.
Есть еще двойной факториал, обозначаемый n!!. Формула его вычисления зависит от четности или нечетности аргумента.
Думаю принцип понятен без дополнительных пояснений.
Кроме того, существует «король факториалов», так называемый суперфакториал, который равен произведению факториалов числа, меньше либо равного данному:
Ну а дальше пошло-поехало: придумали гиперфакториалы, которые равны произведениям суперфакториалов, а потом и вовсе обобщили в m-кратный факториал.
Вот еще несколько интересных свойств факториала и заканчиваем:
1) n! — никогда не является квадратом какого-либо числа.
Источник
Алгоритмы быстрого вычисления факториала
Понятие факториала известно всем. Это функция, вычисляющая произведение последовательных натуральных чисел от 1 до N включительно: N! = 1 * 2 * 3 *… * N. Факториал — быстрорастущая функция, уже для небольших значений N значение N! имеет много значащих цифр.
Попробуем реализовать эту функцию на языке программирования. Очевидно, нам понадобиться язык, поддерживающий длинную арифметику. Я воспользуюсь C#, но с таким же успехом можно взять Java или Python.
Итак, простейшая реализация (назовем ее наивной) получается прямо из определения факториала:
На моей машине эта реализация работает примерно 1,6 секунд для N=50 000.
Далее рассмотрим алгоритмы, которые работают намного быстрее наивной реализации.
Алгоритм вычисления деревом
Первый алгоритм основан на том соображении, что длинные числа примерно одинаковой длины умножать эффективнее, чем длинное число умножать на короткое (как в наивной реализации). То есть нам нужно добиться, чтобы при вычислении факториала множители постоянно были примерно одинаковой длины.
Пусть нам нужно найти произведение последовательных чисел от L до R, обозначим его как P(L, R). Разделим интервал от L до R пополам и посчитаем P(L, R) как P(L, M) * P(M + 1, R), где M находится посередине между L и R, M = (L + R) / 2. Заметим, что множители будут примерно одинаковой длины. Аналогично разобьем P(L, M) и P(M + 1, R). Будем производить эту операцию, пока в каждом интервале останется не более двух множителей. Очевидно, что P(L, R) = L, если L и R равны, и P(L, R) = L * R, если L и R отличаются на единицу. Чтобы найти N! нужно посчитать P(2, N).
Посмотрим, как будет работать наш алгоритм для N=10, найдем P(2, 10):
P(2, 10)
P(2, 6) * P(7, 10)
( P(2, 4) * P(5, 6) ) * ( P(7, 8) * P(9, 10) )
( (P(2, 3) * P(4) ) * P(5, 6) ) * ( P(7, 8) * P(9, 10) )
( ( (2 * 3) * (4) ) * (5 * 6) ) * ( (7 * 8) * (9 * 10) )
( ( 6 * 4 ) * 30 ) * ( 56 * 90 )
( 24 * 30 ) * ( 5 040 )
720 * 5 040
3 628 800
Получается своеобразное дерево, где множители находятся в узлах, а результат получается в корне
Реализуем описанный алгоритм:
Для N=50 000 факториал вычисляется за 0,9 секунд, что почти вдвое быстрее, чем в наивной реализации.
Алгоритм вычисления факторизацией
Второй алгоритм быстрого вычисления использует разложение факториала на простые множители (факторизацию). Очевидно, что в разложении N! участвуют только простые множители от 2 до N. Попробуем посчитать, сколько раз простой множитель K содержится в N!, то есть узнаем степень множителя K в разложении. Каждый K-ый член произведения 1 * 2 * 3 *… * N увеличивает показатель на единицу, то есть показатель степени будет равен N / K. Но каждый K 2 -ый член увеличивает степень еще на единицу, то есть показатель становится N / K + N / K 2 . Аналогично для K 3 , K 4 и так далее. В итоге получим, что показатель степени при простом множителе K будет равен N / K + N / K 2 + N / K 3 + N / K 4 +…
Для наглядности посчитаем, сколько раз двойка содержится в 10! Двойку дает каждый второй множитель (2, 4, 6, 8 и 10), всего таких множителей 10 / 2 = 5. Каждый четвертый дает четверку (2 2 ), всего таких множителей 10 / 4 = 2 (4 и 8). Каждый восьмой дает восьмерку (2 3 ), такой множитель всего один 10 / 8 = 1 (8). Шестнадцать (2 4 ) и более уже не дает ни один множитель, значит, подсчет можно завершать. Суммируя, получим, что показатель степени при двойке в разложении 10! на простые множители будет равен 10 / 2 + 10 / 4 + 10 / 8 = 5 + 2 + 1 = 8.
Если действовать таким же образом, можно найти показатели при 3, 5 и 7 в разложении 10!, после чего остается только вычислить значение произведения:
10! = 2 8 * 3 4 * 5 2 * 7 1 = 3 628 800
Осталось найти простые числа от 2 до N, для этого можно использовать решето Эратосфена:
Эта реализация также тратит примерно 0,9 секунд на вычисление 50 000!
Как справедливо отметил pomme скорость вычисления факториала на 98% зависит от скорости умножения. Попробуем протестировать наши алгоритмы, реализовав их на C++ с использованием библиотеки GMP. Результаты тестирования приведены ниже, по ним получается что алгоритм умножения в C# имеет довольно странную асимптотику, поэтому оптимизация дает относительно небольшой выигрыш в C# и огромный в C++ с GMP. Однако этому вопросу вероятно стоит посвятить отдельную статью.
Все алгоритмы тестировались для N равном 1 000, 2 000, 5 000, 10 000, 20 000, 50 000 и 100 000 десятью итерациями. В таблице указано среднее значение времени работы в миллисекундах.
График с линейной шкалой
График с логарифмической шкалой
Идеи и алгоритмы из комментариев
Хабражители предложили немало интересных идей и алгоритмов в ответ на мою статью, здесь я оставлю ссылки на лучшие из них
Исходные коды реализованных алгоритмов приведены под спойлерами
Источник
Факториал
О чем эта статья:
Факториал: определение
Факториал числа n — это произведение натуральных чисел от 1 до n. Обозначается n, произносится «эн-факториал».
Факториал определен для целых неотрицательных чисел. Это значит, что вот так нельзя:
Число должно быть целое и положительное:
- 3! 56! 12!
| Формула факториала n!=1⋅2⋅3⋅. ⋅(n−2)⋅(n−1)⋅n |
Вычисляется факториал по формуле: путем умножения всех чисел от одного до значения самого числа под факториалом. Факторизация — это разложение функции на множители.
Мы видим, что 4! — это 3!*4
5! — это 4!*5
6! — это 5!*6
Формулы и свойства факториала
Чтобы узнать, как вычислять факториалы быстро — воспользуемся табличкой. Сохраняйте себе и решайте раньше остальных.
| 1! = 1 |
| 2! = 2 |
| 3! = 6 |
| 4! = 24 |
| 5! = 120 |
| 6! = 720 |
| 7! = 5040 |
| 8! = 40320 |
| 9! = 362880 |
| 10! = 3628800 |
| 11! = 39916800 |
| 12! = 479001600 |
| 13! = 6227020800 |
| 14! = 87178291200 |
| 15! = 1307674368000 |
| 16! = 20922789888000 |
| 17! = 355687428096000 |
| 18! = 6402373705728000 |
| 19! = 121645100408832000 |
| 20! = 2432902008176640000 |
| 21! = 51090942171709440000 |
| 22! = 1124000727777607680000 |
| 23! = 25852016738884976640000 |
| 24! = 620448401733239439360000 |
| 25! = 15511210043330985984000000 |
Факториалов в математике 9 класса — полно. Чтобы всегда быть готовым решить пример, запомните основные формулы:
- (n — 1)! = 1*2*3*4*5*. *(n — 2)(n — 1)
- n! = 1*2*3*4*5*. *(n — 2)(n — 1)n
- (n + 1)! = 1*2*3*4*5*. *(n — 2)(n — 1)n(n + 1)
С помощью формулы Стирлинга можно вычислить факториал многоразрядных чисел.
Такая формула дает результат с небольшой погрешностью.
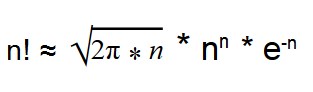 |
Рекуррентная формула
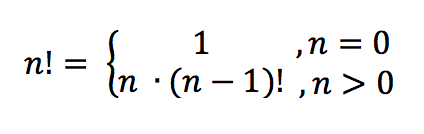 |
- 5! = 5*(5 — 1)! = 5*4! = 5*24 = 120
- 6! = 6*(6-1)! = 6*5! = 6*120 = 720
Для решения примеров обращайтесь к таблице.
Примеры умножения факториалов:
- Пользуйтесь готовой таблицей 5! * 7! = 120 * 5040 = 604800
- Или раскладывайте факториалы отдельно, если хотите потренироваться:
5! = 1*2*3*4*5 = 4! * 5 =120
7! = 1*2*3*4*5*6*7 = 6! * 7 = 5040
120 * 5040 = 604800
Примеры решений
Давайте поупражняемся и решим пару примеров.
1. Сократите дробь:
При сокращении факториалов, пользуйтесь свойством:
n! = (n — 1)! * n
100! = 99! * 100
Далее сокращаем по принципу сокращения обыкновенных дробей.
2. Вычислите значение выражения с факториалом: 8! + 5!
Можно для решения факториалов воспользоваться таблицей и вычислить быстрее.
А можно потренироваться и разложить их:
8! = 1*2*3*4*5*6*7*8 = 7!*8 = 5040 * 8 = 40320
5! = 1*2*3*4*5 = 4!*5 = 120
40320 + 120 = 40440
8! + 5! = 40440
3. Вычислите значение выражения:
7! = 1*2*3*4*5*6*7 = 5! * 6 *7
Далее сокращаем все, что можем сократить (3*2=6, сокращаем числа 6) и получаем ответ.
4. Вычислите значение выражение:
Вы уже знаете, как найти факториал — раскладываем 70 и 49:
70! = 1*2*3*. *69 = 69! * 70
49! = 1*2*3*. 49! * 48
Далее сокращаем все одинаковые множители.
5. Сократите дробь:
Проводим разложение на множители при помощи формул сокращенного умножения (x+1)x(x-1) и сокращаем все одинаковые множители (x-1)!.
Если вы все еще считаете, что факториал бесполезен и не может помочь вам в жизни, то это не так. Он помогает легко вычислять вероятности (а это бывает нужно чаще, чем кажется). К тому же, комбинаторика необходима тем, кто собирается работать в IT. Поэтому решайте побольше задачек на факториалы, в мире будущего без них — никуда.
Источник