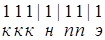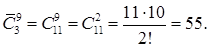14. Сочетания с повторениями
Пусть имеются предметы n различных типов. Сколькими способами можно составить из них комбинацию из k элементов, если не принимать во внимание порядок элементов в комбинации, но при этом предметы одного и того же типа могут повторяться? Иными словами, различные комбинации должны отличаться количеством предметов хотя бы одного типа. Такие комбинации называются сочетаниями с повторениями, а их общее число будем обозначать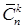 
.
Поясним это на следующем примере. Пусть имеется три элемента: a, b и c. Тогда из этих трёх элементов можно составить шесть сочетаний с повторениями по два элемента: ab, ac, bc, aa, bb, cc.
Таким образом, сочетание с повторениями из n элементов по k элементов (при этом допускается, что m>n) может содержать любой элемент сколько угодно раз от 1 до k включительно или не содержать его совсем, т. е. каждое сочетание с повторениями из n элементов по k элементов может состоять не только из k различных элементов, но и k каких угодно и как угодно повторяющихся элементов.
Следует отметить, что если, например, две комбинации по k элементов отличаются друг от друга только порядком расположения элементов, то они не считаются различными сочетаниями.
Существует специальная формула для вычисления числа сочетаний с повторениями:
(12.1)
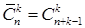
Выведем эту формулу. Прежде всего надо занумеровать возможные типы элементов числами от 1 до n (иначе можно оказаться в положении мужа, который никак не мог вспомнить, что ему поручила купить жена: 5 пакетов молока и 2 банки пива или наоборот 2 пакета молока и 5 банок пива). Теперь можно каждую комбинацию зашифровать с помощью последовательности единиц и палочек: для каждого типа с 1-го до n-го по порядку написать столько единиц, сколько предметов этого типа входит в комбинацию, а различные типы отделять друг от друга палочками.
Например, в кондитерском магазине продаются пирожные 4 видов: корзиночки, наполеоны, песочные и эклеры. Если куплено 3 корзиночки (к), 1 наполеон (н), 2 песочных (п) и 1 эклер (э), то получим такую запись:
В этой записи палочки отделяют одну группу пирожных от другой. Если же куплено 2 корзиночки и 5 песочных, то получим запись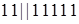 
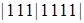
. Ясно, что разным покупкам соответствуют при этом разные комбинации из 7 единиц и 3 палочек. Обратно, каждой комбинации единиц и палочек соответствует какая-то покупка. Например, комбинации 
соответствует покупка 3 наполеонов и 4 песочных (крайние группы отсутствуют).
В результате мы получим столько единиц, сколько предметов входит в комбинацию, т. е. k, а число палочек будет на 1 меньше, чем число типов предметов, т. е. n–1. Таким образом, мы получим перестановки с повторениями из k единиц и n–1 палочек. Различным комбинациям при этом соответствуют различные перестановки с повторениями, а каждой перестановке с повторениями соответствует своя комбинация.
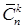
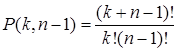
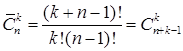
Итак, число сочетаний с повторениями из элементов n типов по k равно числу P(k, n–1) перестановок с повторениями из n–1 палочек и k единиц. А
. Поэтому
.
Пример 12.1. В кондитерской имеется 3 вида пирожных. Сколькими способами можно купить 9 пирожных?
Решение. В задаче требуется найти число всевозможных групп по 9 элементов, которые можно составить из данных трех различных элементов, причем указанные элементы в каждой группе могут повторяться, а сами группы отличаются друг от друга хотя бы одним элементом. Это задача на отыскание числа сочетаний с повторениями из трех элементов по девять. Следовательно,
Пример 12.2. В почтовом отделении продаются открытки 10 сортов. Сколькими способами можно купить в нем 12 открыток? 8 открыток? Сколькими способами можно купить 8 различных открыток?
Решение. Данная задача на отыскание числа сочетаний с повторениями из 10 элементов по 10. Следовательно,
, 
.
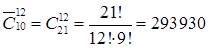
В случае, когда требуется купить 8 различных открыток, получим сочетания без повторений:
.
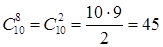
Пример 12.3. Сколько всего чисел (не больше 100000) можно составить из цифр 1, 2, 3, 4 и 5 в каждом из которых цифры расположены в неубывающем порядке?
Решение. Это задача о числе сочетаний из пяти цифр по одному, по два, по три, по четыре и по пяти с повторениями в каждом случае. Поскольку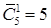 
, 
, 
, 
, 
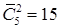
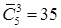
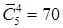
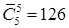
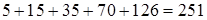
, то существует 
чисел, удовлетворяющих условию задачи.
12.1. Сколькими способами Буратино, кот Базилио и лиса Алиса могут поделить между собой 5 одинаковых золотых монет?
Ответ: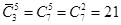 
.
12.2. В кондитерской имеется пять разных сортов пирожных. Сколькими способами можно выбрать набор из четырёх пирожных?
Ответ: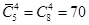 
.
12.3. Сколько существует треугольников, длины сторон которых принимают одно из значений 4, 5, 6, 7?
Ответ: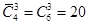 
.
12.4. Сколько можно построить различных прямоугольных параллелепипедов, длина каждого ребра которых является целым числом от 1 до 10?
Ответ: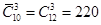 
.
Источник
КОМБИНАТОРИКА
Комбинаторика – раздел математики, который изучает задачи выбора и расположения элементов из некоторого основного множества в соответствии с заданными правилами. Формулы и принципы комбинаторики используются в теории вероятностей для подсчета вероятности случайных событий и, соответственно, получения законов распределения случайных величин. Это, в свою очередь, позволяет исследовать закономерности массовых случайных явлений, что является весьма важным для правильного понимания статистических закономерностей, проявляющихся в природе и технике.
Правила сложения и умножения в комбинаторике
Правило суммы. Если два действия А и В взаимно исключают друг друга, причем действие А можно выполнить m способами, а В – n способами, то выполнить одно любое из этих действий (либо А, либо В) можно n + m способами.
Пример 1.
В классе учится 16 мальчиков и 10 девочек. Сколькими способами можно назначить одного дежурного?
Дежурным можно назначить либо мальчика, либо девочку, т.е. дежурным может быть любой из 16 мальчиков, либо любая из 10 девочек.
По правилу суммы получаем, что одного дежурного можно назначить 16+10=26 способами.
Правило произведения. Пусть требуется выполнить последовательно k действий. Если первое действие можно выполнить n1 способами, второе действие n2 способами, третье – n3 способами и так до k-го действия, которое можно выполнить nk способами, то все k действий вместе могут быть выполнены:
Пример 2.
В классе учится 16 мальчиков и 10 девочек. Сколькими способами можно назначить двух дежурных?
Первым дежурным можно назначить либо мальчика, либо девочку. Т.к. в классе учится 16 мальчиков и 10 девочек, то назначить первого дежурного можно 16+10=26 способами.
После того, как мы выбрали первого дежурного, второго мы можем выбрать из оставшихся 25 человек, т.е. 25-ю способами.
По теореме умножения двое дежурных могут быть выбраны 26*25=650 способами.
Сочетания без повторений. Сочетания с повторениями
Классической задачей комбинаторики является задача о числе сочетаний без повторений, содержание которой можно выразить вопросом: сколькими способами можно выбрать m из n различных предметов ?
Пример 3.
Необходимо выбрать в подарок 4 из 10 имеющихся различных книг. Сколькими способами можно это сделать?
Нам из 10 книг нужно выбрать 4, причем порядок выбора не имеет значения. Таким образом, нужно найти число сочетаний из 10 элементов по 4:
.
Рассмотрим задачу о числе сочетаний с повторениями: имеется по r одинаковых предметов каждого из n различных типов; сколькими способами можно выбрать m (
) из этих (n*r) предметов?
.
Пример 4.
В кондитерском магазине продавались 4 сорта пирожных: наполеоны, эклеры, песочные и слоеные. Сколькими способами можно купить 7 пирожных?
Т.к. среди 7 пирожных могут быть пирожные одного сорта, то число способов, которыми можно купить 7 пирожных, определяется числом сочетаний с повторениями из 7 по 4.
.
Размещения без повторений. Размещения с повторениями
Классической задачей комбинаторики является задача о числе размещений без повторений, содержание которой можно выразить вопросом: сколькими способами можно выбрать и разместить по m различным местам m из n различных предметов?
Пример 5.
В некоторой газете 12 страниц. Необходимо на страницах этой газеты поместить четыре фотографии. Сколькими способами можно это сделать, если ни одна страница газеты не должна содержать более одной фотографии?
В данной задаче мы не просто выбираем фотографии, а размещаем их на определенных страницах газеты, причем каждая страница газеты должна содержать не более одной фотографии. Таким образом, задача сводится к классической задаче об определении числа размещений без повторений из 12 элементов по 4 элемента:
Таким образом, 4 фотографии на 12 страницах можно расположить 11880 способами.
Также классической задачей комбинаторики является задача о числе размещений с повторениями, содержание которой можно выразить вопросом: сколькими способами можно выбрать и разместить по m различным местам m из n предметов, среди которых есть одинаковые?
Пример 6.
У мальчика остались от набора для настольной игры штампы с цифрами 1, 3 и 7. Он решил с помощью этих штампов нанести на все книги пятизначные номера– составить каталог. Сколько различных пятизначных номеров может составить мальчик?
Можно считать, что опыт состоит в 5-кратном выборе с возращением одной из 3 цифр (1, 3, 7). Таким образом, число пятизначных номеров определяется числом размещений с повторениями из 3 элементов по 5:
.
Перестановки без повторений. Перестановки с повторениями
Классической задачей комбинаторики является задача о числе перестановок без повторения, содержание которой можно выразить вопросом: сколькими способами можно разместить n различных предметов на n различных местах?
Пример 7.
Сколько можно составить четырехбуквенных «слов» из букв слова«брак»?
Генеральной совокупностью являются 4 буквы слова «брак» (б, р, а, к). Число «слов» определяется перестановками этих 4 букв, т. е.
Для случая, когда среди выбираемых n элементов есть одинаковые (выборка с возвращением), задачу о числе перестановок с повторениями можно выразить вопросом: сколькими способами можно переставить n предметов, расположенных на n различных местах, если среди n предметов имеются k различных типов (k
Пример 8.
Сколько разных буквосочетаний можно сделать из букв слова «Миссисипи»?
Здесь 1 буква «м», 4 буквы «и», 3 буквы «c» и 1 буква «п», всего 9 букв. Следовательно, число перестановок с повторениями равно
ОПОРНЫЙ КОНСПЕКТ ПО РАЗДЕЛУ «КОМБИНАТОРИКА»
Источник
