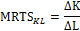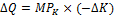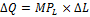Взаимозаменяемость ресурсов. Изокванта.
Один и тот же объект выпуска продукции может быть достигнут при различных сочетаниях факторов. Для фирмы, стремящейся к максимизации прибыли, наилучшей комбинацией факторов окажется та, которая обеспечивает наименьшие издержки => задача фирмы сводится к обеспечению минимизации издержек при каждом заданном объеме производства.
Для выявления всех возможных комбинаций факторов при выпуске заданного объема продукции в экономической теории используется понятие изокванты. Изокванта – кривая, любая точка на которой показывает различные комбинации двух переменных факторов, обеспечивающие один и тот же объем выпуска продукции. Все комбинации факторов производства, представленные на изокванте, являются технологически эффективными.
Свойства:
— изокванты никогда не пересекаются в силу действия принципа транзитивности (транзитивность означает следующее: если какая-то альтернатива А предпочтительнее, чем альтернатива Б, а альтернатива Б предпочтительнее С, то альтернатива А предпочтительнее С, в данном случает альтернативы – это изокванты). Каждой изокванте соответствует определенный объем выпуска продукции, причем чем дальше изокванта отстоит от начала координат, тем больший объем выпуска обеспечивается.
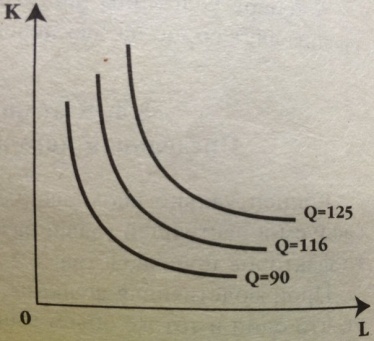
— изокванты имею т отрицательный наклон, т.к. для сохранения неизменным объема выпуска продукции при уменьшении использования одного фактора необходимо увеличить применение другого фактора.
— изокванты становятся более пологими по мере продвижения сверху вниз вдоль них. В верхней части части изокванты для выпуска заданного объема продукции используется большое количество капитала и незначительное количество труда. При движении вниз вдоль изокванты требуется все больше единиц труда для замещения каждой единицы капитала, вследствие падение предельной производительности труда по мере наращивания его количества. Этим объясняется выпуклая по отношению к началу координат форма изоквант.
С помощью наклона изоквант можно определить степень замещения одного фактора производства другим. Например, фирма производит продукцию с использованием двух переменных факторов: капитала (K) и труда (L). Начнем двигаться вниз по изокванте с объемом выпуска (Q), равным 116 единиц, сокращая количество применяемого капитала. Для того, чтобы остаться на этой же изокванте, т.е. обеспечить тот же объем производства, фирме потребуется увеличить количество применяемого труда. Отношение изменения в количестве одного фактора к изменению в количестве другого фактора при сохранении неизменным объема производства называется предельной нормой технологического замещения (MRTS):
В данном случае, MRTS – пропорция замещения капитала трудом при условии, что мы остаемся на той же самой изокванте с объемом в 116 единиц.
Наклон кривой в каждой точке определяется наклоном касательной в данной точке, который равен отношению величины изменения фактора K к величине изменения фактора L (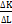 
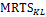
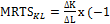
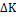
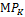
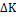
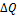
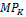
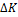
) => наклон изокванты равен предельной норме технологического замещения. Т. К. изокванта имеет отрицательный наклон, 
в любой точке будет равна наклону касательной в данной точке, умноженной на -1, т.е.
).
Предельная норма технологического замещения непосредственно связана с предельными продуктами факторов производства. Сокращая количество одного из факторов, например капитала ( 
), фирма тем самым уменьшает объем выпуска продукции на определенную величину. Эта величина равна произведению предельного продукта капитала ( 
) и изменения в его количестве ( )
– изменение в объеме выпуска продукции.
— предельный продукт капитала.
— изменение количества применяемого капитала.
Для того, чтобы остаться на той же изокванте, сокращение объема производства должно быть компенсировано увеличением количеством применяемого труда ( 
, т.е.
– предельный продукт труда,
— изменение количества применяемого труда.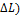
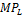
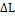
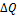
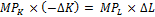
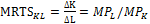
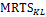
=> абсолютное значение равно в данных уравнениях =>
=>
= наклону изокванты
Изокванты имеют выпуклую по отношению к началу координат форму т.к. по мере движения вниз по изокванте уменьшается. Пояснение: по мере увеличения количества фактора L его определенный продукт уменьшается относительно предельного продукта фактора K. => сокращение применяемого фактора R ведет к росту его предельного продукта. Знаменатель в уравнении будет расти, а числитель будет уменьшаться.
Три различных типа изоквант, отличающиеся степенью взаимозаменяемости ресурсов.
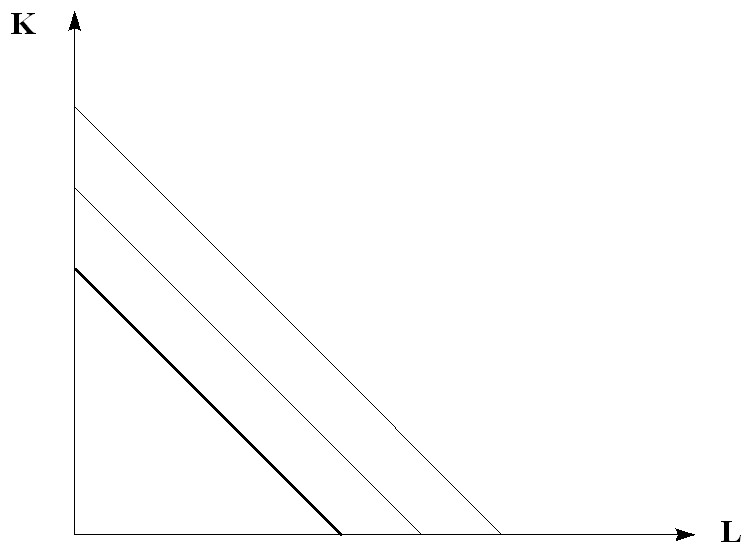
1) Абсолютная заменяемость:
Заданный объем выпуска продукции может быть обеспечен как путем использования какого-либо одного из двух переменных ресурсов, так и путем их комбинаций. Изокванта будет иметь вид прямой линии, а MRTS будет постоянной величиной. Например, нефть и газ являются абсолютно заменяемыми.
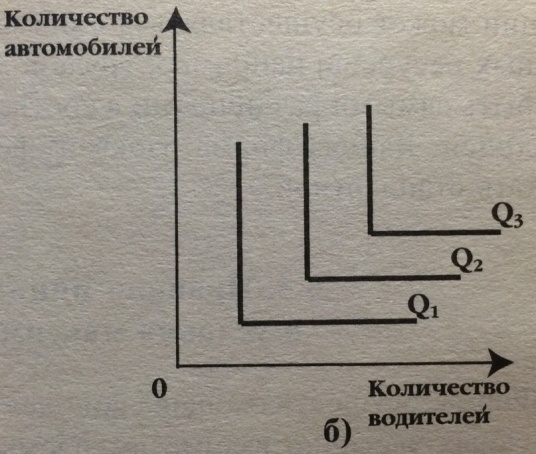
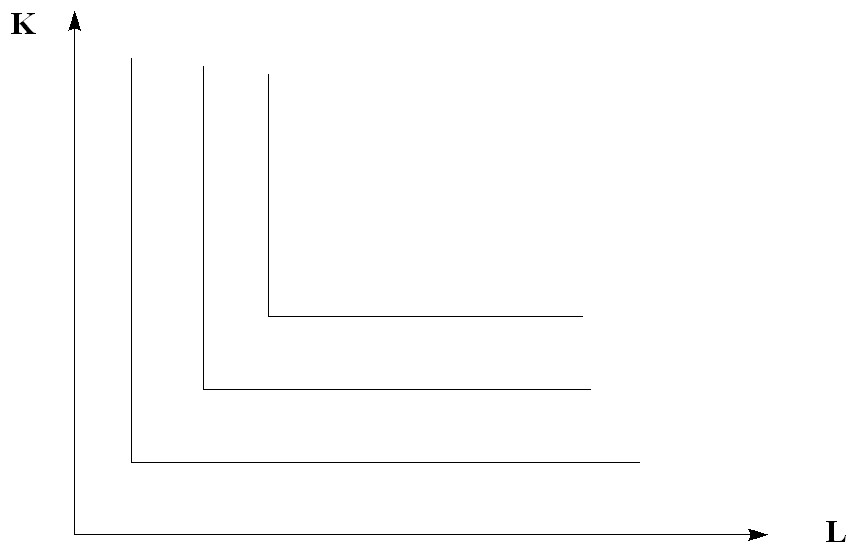
2) Абсолютная комплементарность:
Два переменных ресурса, используемых для производства данного вида продукции, имеют одну определенную пропорцию. Заданная производственная функция предполагает наличие единственно возможной комбинации ресурсов. В данном случае MRTS = 0, а изокванта будет иметь вид прямого угла. Обязательным условием перехода на более высокую изокванту такого вида является соблюдение заданной пропорциональности в использовании ресурсов. Если будет изменение одного ресурса без соответствующего изменения в количестве другого, то перейти на другую изокванту не представляется возможным. При преходе на более высокую изокванту, как правило, происходит при неизменной пропорции 1:1.
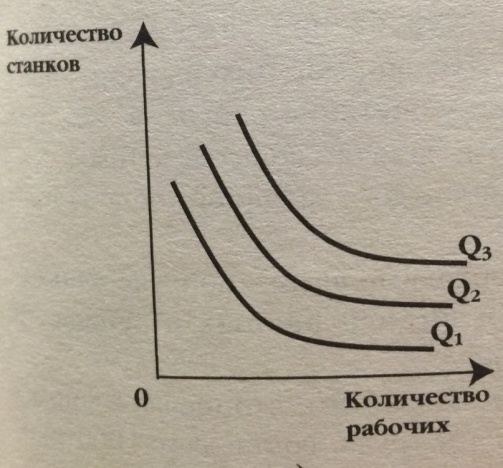
3) Частичная взаимозаменяемость:
Производство продукции может осуществляться с обязательным использованием двух перемнных ресурсов, например, труда и капитала. Однако их комбинации могут быть самыми различными в соответствии с заданной производственной функцией. Данная форма изоквант встречается чаще всего, и ее принято считать стандартной.
Источник
Изокванта и ее типы
При моделировании потребительского спроса один и тот же уровень полезности различных комбинаций потребительских благ графически отображается с помощью кривой безразличия.
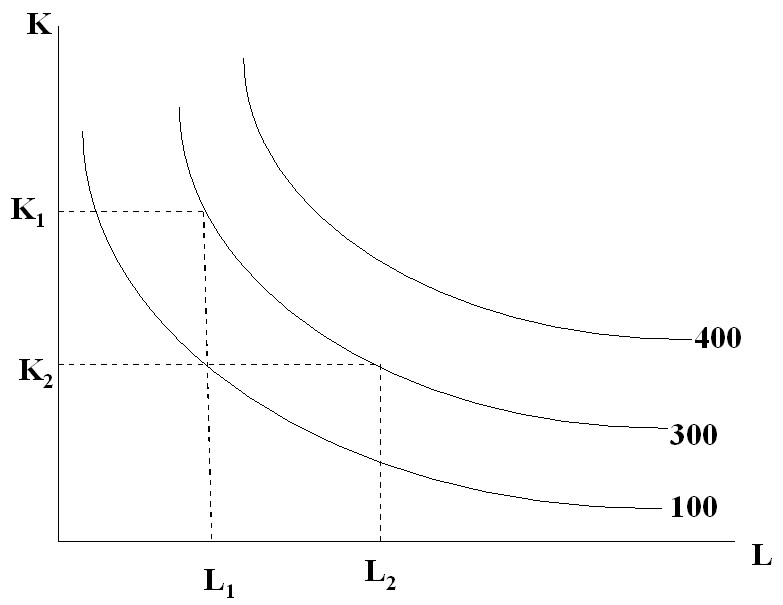
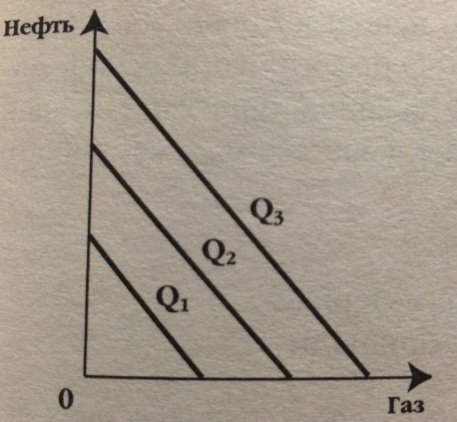
В экономико-математических моделях производства каждая технология графически может быть представлена точкой, координаты которой отражают минимально необходимые затраты ресурсов K и L для производства данного объема выпуска. Множество таких точек образуют линию равного выпуска, или изокванту. Таким образом, производственная функция графически представляется семейством изоквант. Чем дальше от начала координат расположена изокванта, тем больший объем производства она отражает. В отличие от кривой безразличия каждая изокванта характеризует количественно определенный объем выпуска. На рис. 6.1 представлено три изокванты, соответствующие объему производства в 200, 300 и 400 единиц продукции.
Рис. 6.1. Изокванты, соответствующие различному объему производства
Можно сказать, что для выпуска 300 единиц продукции необходимо K1 единиц капитала и L1 единиц труда или K2 единиц капитала или L2 единиц труда, или любая другая их комбинация из того множества, которое представлено изоквантой Y2=300.
В общем случае в множестве X допустимых наборов производственных факторов выделяется подмножество Xc, называемое изоквантой производственной функции, которое характеризуется тем, что для всякого вектора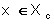 
справедливо равенство:
Таким образом, для всех наборов ресурсов, соответствующих изокванте, оказываются равными объемы выпускаемой продукции. По существу изокванта представляет собой описание возможности взаимной замены факторов в процессе производства продукции, обеспечивающей неизменный объем производства. В связи с этим оказывается возможным определить коэффициент взаимной замены ресурсов, используя дифференциальное соотношение вдоль любой изокванты
.
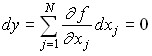
Отсюда коэффициент эквивалентной замены пары факторов j и k равен:
.
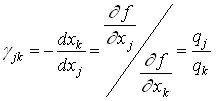
Полученное соотношение показывает, что, если производственные ресурсы замещаются в отношении, равном отношению приростных продуктивностей, то количество производимой продукции остается неизменным. Нужно сказать, что знание производственной функции позволяет охарактеризовать масштабы возможности осуществить взаимную замену ресурсов в эффективных технологических способах. Для достижения этой цели служит коэффициент эластичности замены ресурсов по продукции:
,
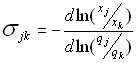
который вычисляется вдоль изокванты при неизменном уровне затрат прочих производственных факторов. Величина σjk представляет собой характеристику относительного изменения коэффициента взаимной замены ресурсов при изменении соотношения между ними. Если отношение взаимозаменяемых ресурсов изменится на σjk процентов, то коэффициент взаимной замены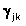 
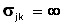
изменится на 1 процент. В случае линейной производственной функции коэффициент взаимной замены остается неизменным при любом соотношении используемых ресурсов и поэтому можно считать, что эластичность 
. Соответственно большие значения σjk свидетельствуют о том, что возможна большая свобода в замене производственных факторов вдоль изокванты и при этом основные характеристики производственной функции (продуктивности, коэффициент взаимозамены) будут меняться очень слабо.
Для степенных производственных функций для любой пары взаимозаменяемых ресурсов справедливо равенство σjk=1. В практике прогнозирования и предплановых расчетов часто используются функции постоянной эластичности замены (СЕS), имеющие вид:
.
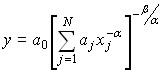
Для такой функции коэффициент эластичности замены ресурсов:
и не меняется в зависимости от объема и отношения затрачиваемых ресурсов. При малых значениях σjk ресурсы могут заменять друг друга лишь в незначительных размерах, а в пределе при σjk=0 они теряют свойство взаимозаменяемости и выступают в процессе производства лишь в постоянном отношении, т.е. являются взаимодополняющими. Примером производственной функции, описывающей производство в условиях использования взаимодополняющих ресурсов является функция «выпуска-затрат», которая имеет вид:
,
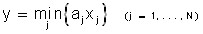
где aj – постоянный коэффициент ресурсоотдачи j-того производственного фактора. Нетрудно видеть, что производственная функция такого типа определяет выпуск по «узкому месту» на множестве используемых производственных факторов. Различные случаи поведения изоквант производственных функций для различных значений коэффициентов эластичности замены представлены на графике (рис. 6.2).
Представление эффективного технологического множества с помощью скалярной производственной функции оказывается недостаточным в тех случаях, когда нельзя обойтись единственным показателем, описывающим результаты деятельности производственного объекта, но необходимо использовать несколько (М) выходных показателей. В этих условиях можно использовать векторную производственную функцию:
,
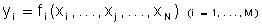
Рис. 6.2. Различные случаи поведения изоквант
Важное понятие предельной (дифференциальной) продуктивности вводится соотношением:
,
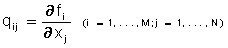
Аналогичное обобщение допускают все остальные главные характеристики скалярных ПФ.
Подобно кривым безразличия изокванты также подразделяются на различные типы.
Для линейной производственной функции вида:
Y = A + b1K + b2L ,где
Y – объем производства;
A, b1, b2 — параметры;
K, L – затраты капитала и туда,
и полном замещении одного ресурса другим изокванта будет иметь линейную форму (рис. 6.3).
Рис. 6.3. Изокванты линейного типа
Для степенной производственной функции Y = AKαLβ будут иметь вид кривых (рис. 6.4).
Рис. 6.4. Изокванты степенной производственной функции
Если изокванта отражает лишь один технологический способ производства данного продукта, то труд и капитал комбинируются в единственно возможном сочетании (рис.6.5).
Рис. 6.5. Изокванты при жесткой дополняемости ресурсов
Такие изокванты иногда называют изоквантами леонтьевского типа, по имени американского экономиста В.В.Леонтьева, который положил такой тип изокванты в основу разработанного им метода input-output (затраты – выпуск).
Изокванты подобной конфигурации используются в линейном программировании для обоснования теории оптимального распределения ресурсов. Ломаные изокванты наиболее реалистично представляют технологические возможности многих производственных объектов. Однако, в экономической теории традиционно используют главным образом кривые изокванты, которые получаются из ломаных при увеличении числа технологий и увеличении соответственно точек излома.
Источник
