Еще один способ доказательства теоремы пифагора

Разные способы доказательства теоремы Пифагора: примеры, описание и отзывы

В одном можно быть уверенным на все сто процентов, что на вопрос, чему равен квадрат гипотенузы, любой взрослый человек смело ответит: «Сумме квадратов катетов». Эта теорема прочно засела в сознании каждого образованного человека, но достаточно лишь попросить кого-либо ее доказать, и тут могут возникнуть сложности. Поэтому давайте вспомним и рассмотрим разные способы доказательства теоремы Пифагора.

Краткий обзор биографии

Теорема Пифагора знакома практически каждому, но почему-то биография человека, который произвел ее на свет, не так популярна. Это поправимо. Поэтому прежде чем изучить разные способы доказательства теоремы Пифагора, нужно кратко познакомиться с его личностью.

Пифагор – философ, математик, мыслитель родом из Древней Греции. Сегодня очень сложно отличить его биографию от легенд, которые сложились в память об этом великом человеке. Но как следует из трудов его последователей, Пифагор Самосский родился на острове Самос. Его отец был обычный камнерез, а вот мать происходила из знатного рода.

Судя по легенде, появление на свет Пифагора предсказала женщина по имени Пифия, в чью честь и назвали мальчика. По ее предсказанию рожденный мальчик должен был принести много пользы и добра человечеству. Что вообще-то он и сделал.

Рождение теоремы

В юности Пифагор переехал с острова Самос в Египет, чтобы встретиться там с известными египетскими мудрецами. После встречи с ними он был допущен к обучению, где и познал все великие достижения египетской философии, математики и медицины.

Вероятно, именно в Египте Пифагор вдохновился величеством и красотой пирамид и создал свою великую теорию. Это может шокировать читателей, но современные историки считают, что Пифагор не доказывал свою теорию. А лишь передал свое знание последователям, которые позже и завершили все необходимые математические вычисления.

Как бы там ни было, сегодня известна не одна методика доказательства данной теоремы, а сразу несколько. Сегодня остается лишь гадать, как именно древние греки производили свои вычисления, поэтому здесь рассмотрим разные способы доказательства теоремы Пифагора.

Теорема Пифагора

Прежде чем начинать какие-либо вычисления, нужно выяснить, какую теорию предстоит доказать. Теорема Пифагора звучит так: «В треугольнике, у которого один из углов равен 90 о , сумма квадратов катетов равна квадрату гипотенузы».

Всего существует 15 разных способов доказательства теоремы Пифагора. Это достаточно большая цифра, поэтому уделим внимание самым популярным из них.

Способ первый

Сначала обозначим, что нам дано. Эти данные будут распространяться и на другие способы доказательств теоремы Пифагора, поэтому стоит сразу запомнить все имеющееся обозначения.

Допустим, дан прямоугольный треугольник, с катетами а, в и гипотенузой, равной с. Первый способ доказательства основывается на том, что из прямоугольного треугольника нужно дорисовать квадрат.

Чтобы это сделать, нужно к катету длиной а дорисовать отрезок равный катету в, и наоборот. Так должно получиться две равные стороны квадрата. Остается только нарисовать две параллельные прямые, и квадрат готов.

Внутри получившейся фигуры нужно начертить еще один квадрат со стороной равной гипотенузе исходного треугольника. Для этого от вершин ас и св нужно нарисовать два параллельных отрезка равных с. Таким образом, получиться три стороны квадрата, одна из которых и есть гипотенуза исходного прямоугольного треугольники. Остается лишь дочертить четвертый отрезок.

На основании получившегося рисунка можно сделать вывод, что площадь внешнего квадрата равна (а+в) 2 . Если заглянуть внутрь фигуры, можно увидеть, что помимо внутреннего квадрата в ней имеется четыре прямоугольных треугольника. Площадь каждого равна 0,5ав.

Поэтому площадь равна: 4*0,5ав+с 2 =2ав+с 2

Отсюда (а+в) 2 =2ав+с 2

И, следовательно, с 2 =а 2 +в 2

Способ два: подобные треугольники

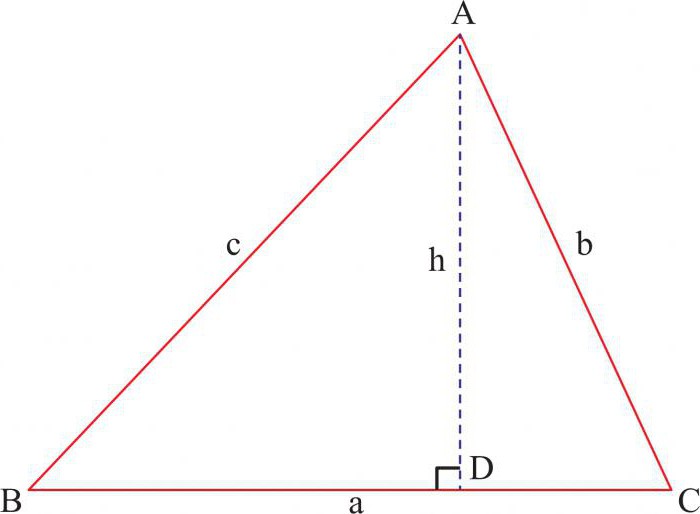
Данная формула доказательства теоремы Пифагора была выведена на основании утверждения из раздела геометрии о подобных треугольниках. Оно гласит, что катет прямоугольного треугольника – среднее пропорциональное для его гипотенузы и отрезка гипотенузы, исходящего из вершины угла 90 о .

Исходные данные остаются те же, поэтому начнем сразу с доказательства. Проведем перпендикулярный стороне АВ отрезок СД. Основываясь на вышеописанном утверждении катеты треугольников равны:

Чтобы ответить на вопрос, как доказать теорему Пифагора, доказательство нужно проложить возведением в квадрат обоих неравенств.

АС 2 =АВ*АД и СВ 2 =АВ*ДВ

Теперь нужно сложить получившиеся неравенства.

АС 2 + СВ 2 =АВ*(АД*ДВ), где АД+ДВ=АВ

АС 2 + СВ 2 =АВ*АВ

АС 2 + СВ 2 =АВ 2

Доказательство теоремы Пифагора и различные способы ее решения нуждаются в разностороннем подходе к данной задаче. Однако этот вариант является одним из простейших.

Еще одна методика расчетов

Описание разных способов доказательства теоремы Пифагора могут ни о чем не сказать, до тех самых пор пока самостоятельно не приступишь к практике. Многие методики предусматривают не только математические расчеты, но и построение из исходного треугольника новых фигур.

В данном случае необходимо от катета ВС достроить еще один прямоугольный треугольник ВСД. Таким образом, теперь имеется два треугольника с общим катетом ВС.

Зная, что площади подобных фигур имеют соотношение как квадраты их сходных линейных размеров, то:

Поскольку из разных способов доказательств теоремы Пифагора для 8 класса этот вариант едва ли подойдет, можно воспользоваться следующей методикой.

Самый простой способ доказать теорему Пифагора. Отзывы

Как полагают историки, этот способ был впервые использован для доказательства теоремы еще в древней Греции. Он является самым простым, так как не требует абсолютно никаких расчетов. Если правильно начертить рисунок, то доказательство утверждения, что а 2 +в 2 =с 2 , будет видно наглядно.

Условия для данного способа будет немного отличаться от предыдущего. Чтобы доказать теорему, предположим, что прямоугольный треугольник АВС – равнобедренный.

Гипотенузу АС принимаем за сторону квадрата и дочерчиваем три его стороны. Кроме этого необходимо провести две диагональные прямые в получившемся квадрате. Таким образом, чтобы внутри него получилось четыре равнобедренных треугольника.

К катетам АВ и СВ так же нужно дочертить по квадрату и провести по одной диагональной прямой в каждом из них. Первую прямую чертим из вершины А, вторую – из С.

Теперь нужно внимательно всмотреться в получившийся рисунок. Поскольку на гипотенузе АС лежит четыре треугольника, равные исходному, а на катетах по два, это говорит о правдивости данной теоремы.

Кстати, благодаря данной методике доказательства теоремы Пифагора и появилась на свет знаменитая фраза: «Пифагоровы штаны во все стороны равны».

Доказательство Дж. Гарфилда

Джеймс Гарфилд – двадцатый президент Соединенных Штатов Америки. Кроме того, что он оставил свой след в истории как правитель США, он был еще и одаренным самоучкой.

В начале своей карьеры он был обычным преподавателем в народной школе, но вскоре стал директором одного из высших учебных заведений. Стремление к саморазвитию и позволило ему предложить новую теорию доказательства теоремы Пифагора. Теорема и пример ее решения выглядит следующим образом.

Сначала нужно начертить на листе бумаги два прямоугольных треугольника таким образом, чтобы катет одного из них был продолжением второго. Вершины этих треугольников нужно соединить, чтобы в конечном итоге получилась трапеция.

Как известно, площадь трапеции равна произведению полусуммы ее оснований на высоту.

Если рассмотреть получившуюся трапецию, как фигуру, состоящую из трех треугольников, то ее площадь можно найти так:

Теперь необходимо уравнять два исходных выражения

О теореме Пифагора и способах ее доказательства можно написать не один том учебного пособия. Но есть ли в нем смысл, когда эти знания нельзя применить на практике?

Практическое применение теоремы Пифагора

К сожалению, в современных школьных программах предусмотрено использование данной теоремы только в геометрических задачах. Выпускники скоро покинут школьные стены, так и не узнав, а как они могут применить свои знания и умения на практике.

На самом же деле использовать теорему Пифагора в своей повседневной жизни может каждый. Причем не только в профессиональной деятельности, но и в обычных домашних делах. Рассмотрим несколько случаев, когда теорема Пифагора и способы ее доказательства могут оказаться крайне необходимыми.

Связь теоремы и астрономии

Казалось бы, как могут быть связаны звезды и треугольники на бумаге. На самом же деле астрономия – это научная сфера, в которой широко используется теорема Пифагора.

Например, рассмотрим движение светового луча в космосе. Известно, что свет движется в обе стороны с одинаковой скоростью. Траекторию АВ, которой движется луч света назовем l. А половину времени, которое необходимо свету, чтобы попасть из точки А в точку Б, назовем t. И скорость луча – c. Получается, что: c*t=l

Если посмотреть на этот самый луч из другой плоскости, например, из космического лайнера, который движется со скоростью v, то при таком наблюдении тел их скорость изменится. При этом даже неподвижные элементы станут двигаться со скоростью v в обратном направлении.

Допустим, комический лайнер плывет вправо. Тогда точки А и В, между которыми мечется луч, станут двигаться влево. Причем, когда луч движется от точки А в точку В, точка А успевает переместиться и, соответственно, свет уже прибудет в новую точку С. Чтобы найти половину расстояния, на которое сместилась точка А, нужно скорость лайнера умножить на половину времени путешествия луча (t’).

А чтобы найти, какое расстояние за это время смог пройти луч света, нужно обозначить половину пути новой буковой s и получить следующее выражение:

Если представить, что точки света С и В, а также космический лайнер – это вершины равнобедренного треугольника, то отрезок от точки А до лайнера разделит его на два прямоугольных треугольника. Поэтому благодаря теореме Пифагора можно найти расстояние, которое смог пройти луч света.

Этот пример, конечно, не самый удачный, так как только единицам может посчастливиться опробовать его на практике. Поэтому рассмотрим более приземленные варианты применения этой теоремы.

Радиус передачи мобильного сигнала

Современную жизнь уже невозможно представить без существования смартфонов. Но много ли было бы от них прока, если бы они не могли соединять абонентов посредством мобильной связи?!

Качество мобильной связи напрямую зависит от того, на какой высоте находиться антенна мобильного оператора. Для того чтобы вычислить, каком расстоянии от мобильной вышки телефон может принимать сигнал, можно применить теорему Пифагора.

Допустим, нужно найти приблизительную высоту стационарной вышки, чтобы она могла распространять сигнал в радиусе 200 километров.

АВ (высота вышки) = х;

ВС (радиус передачи сигнала) = 200 км;

ОС (радиус земного шара) = 6380 км;

Применив теорему Пифагора, выясним, что минимальная высота вышки должна составить 2,3 километра.

Теорема Пифагора в быту

Как ни странно, теорема Пифагора может оказаться полезной даже в бытовых делах, таких как определение высоты шкафа-купе, например. На первый взгляд, нет необходимости использовать такие сложные вычисления, ведь можно просто снять мерки с помощью рулетки. Но многие удивляются, почему в процессе сборки возникают определенные проблемы, если все мерки были сняты более чем точно.

Дело в том, что шкаф-купе собирается в горизонтальном положении и только потом поднимается и устанавливается к стене. Поэтому боковина шкафа в процессе подъема конструкции должна свободно проходить и по высоте, и по диагонали помещения.

Предположим, имеется шкаф-купе глубиной 800 мм. Расстояние от пола до потолка – 2600 мм. Опытный мебельщик скажет, что высота шкафа должна быть на 126 мм меньше, чем высота помещения. Но почему именно на 126 мм? Рассмотрим на примере.

При идеальных габаритах шкафа проверим действие теоремы Пифагора:

АС=√2474 2 +800 2 =2600 мм – все сходится.

Допустим, высота шкафа равна не 2474 мм, а 2505 мм. Тогда:

АС=√2505 2 +√800 2 =2629 мм.

Следовательно, этот шкаф не подойдет для установки в данном помещении. Так как при поднятии его в вертикальное положение можно нанести ущерб его корпусу.

Пожалуй, рассмотрев разные способы доказательства теоремы Пифагора разными учеными, можно сделать вывод, что она более чем правдива. Теперь можно использовать полученную информацию в своей повседневной жизни и быть полностью уверенным, что все расчеты будут не только полезны, но и верны.

Источник

Малоизвестное обобщение теоремы Пифагора

Вокруг да около

История теоремы Пифагора уходит в века и тысячелетия. В этой статье, мы не будем подробно останавливаться на исторических темах. Для интриги, скажем только, что, по-видимому, эту теорему знали еще древне-египетские жрецы, жившие более 2000 лет до нашей эры. Для тех, кому любопытно, вот ссылка на статью в Википедии.

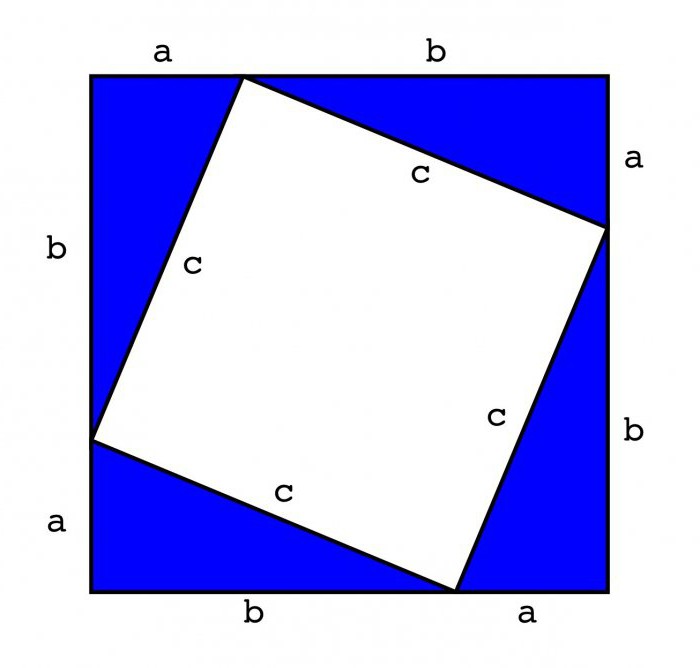
Прежде всего, хочется для полноты изложения привести здесь доказательство теоремы Пифагора, которое, по моему мнению, наиболее элегантно и очевидно. На рисунке выше изображено два одинаковых квадрата: левый и правый. Из рисунка видно, что слева и справа площади закрашенных фигур равны, так как в каждом из больших квадратов закрашено по 4 одинаковых прямоугольных треугольника. А это означает, что и незакрашенные (белые) площади слева и справа тоже равны. Замечаем, что в первом случае площадь незакрашенной фигуры равна , а во втором — площадь незакрашенной области равна . Таким образом, . Теорема доказана!

Зарождение идеи

В этой статье я хочу не только рассказать что-то новое и познавательное о теореме Пифагора, но и поделиться своей историей о том, как в моей голове зародилась интересная идея, которую я сумел сформулировать, доказать и даже предположил возможность обобщения на более высокую размерность. Но обо всем по порядку.

Египетские треугольники

Во-первых, это красивые математические объекты. А во-вторых, с ними очень удобно решать задачи! Нет никаких квадратных корней и иррациональных чисел в ответе.

Загадочные четверки

Заметив такое удивительное совпадение, я стал думать. Вопрос, который меня занимал в связи с этим загадочным обстоятельством, наличием не только троек, но и четверок, обнаруживающих свойства египетского треугольника, был таков: «А что бы это все могло значить?» Я перебирал варианты, какие только приходили в голову. В фантазии себя никак не ограничивал. Много раз садился за стол, выписывал известные мне наборы четверок и вдумчиво на них смотрел… часами… без перерыва… и… ничего не происходило. У меня был школьный товарищ Саня, с которым я как-то поделился своими идеями. Но его больше интересовали гуманитарные науки. Он стал юристом и сейчас служит в звании майора милиции. Саня сказал мне примерно следующее:«Вот странный ты человек. Делать тебе больше нечего. Мало тебе задают домашек? Хватит думать о всякой ерунде!». А, надо сказать, думал я, не переставая, и думал много лет, время от времени возвращаясь к этой загадке. Еще будучи школьником, я сделал вывод, что это, вероятнее всего, имеет отношение к великой теореме Ферма (на которую я тоже много раз подолгу смотрел). Шли годы. Ничего не получалось. Озарение не приходило. И я понял, что, вероятно, дальше чем «что-то связанное с теоремой Ферма» я никуда уже не продвинусь. Но не тут то было

Шерлок нашел зацепку

Итак, в 2014 году ехал я в автобусе по Новосибирску. А может быть это было метро. Дорога не близкая. Заняться нечем. И в очередной раз решил я подумать о моей школьной загадке. И вот что я подумал.

Как же назвать эти числа? Треугольниками не назовешь, ведь четыре числа никак не могут образовать треугольник. И тут! Как гром среди ясного неба

Раз есть такие четверки чисел, значит должен быть геометрический объект с такими же свойствами, отраженными в этих числах!

Теперь осталось только подобрать какой-то геометрический объект под это свойство, и все встанет на свои места! Конечно, предположение было чисто гипотетическое, и никакого подтверждения под собой не имело. Но что если это так!

Начался перебор объектов. Звезды, многоугольники, правильные, неправильные, с прямым углом и так далее и тому подобное. Опять ничего не подходит. Что делать? И в этот момент Шерлок получает свою вторую зацепку.

Надо повысить размерность! Раз тройке соответствуют треугольник на плоскости, значит четверке соответствует нечто трехмерное!

О нет! Опять перебор вариантов! А в трехмерии гораздо, гораздо больше всевозможных геометрических тел. Попробуй перебрать их все! Но не все так плохо. Есть же еще прямой угол и другие зацепки! Что мы имеем? Египетские четверки чисел (пусть будут египетские, надо же их как-то называть), прямой угол (или углы) и некий трехмерный объект. Дедукция сработала! И… Полагаю, что догадливые читатели уже поняли, что речь идет о пирамидах, у которых при одной из вершин все три угла — прямые. Можно даже назвать их прямоугольными пирамидами по аналогии с прямоугольным треугольником.

Новая теорема

Итак, у нас есть все что нужно. Прямоугольные (!) пирамиды, боковые грани-катеты и секущая грань-гипотенуза. Пришло время нарисовать еще одну картинку.

Теорема Пифагора для прямоугольной пирамиды

На картинке изображена пирамида с вершиной в начале прямоугольных координат (пирамида как бы лежит на боку). Пирамида образована тремя взаимно-перпендикулярными векторами, отложенными из начала координат вдоль координатных осей. То есть каждая боковая грань пирамиды — это прямоугольный треугольник с прямым углом при начале координат. Концы векторов определяют секущую плоскость и образуют грань-основание пирамиды.

Теорема

Пусть есть прямоугольная пирамида, образованная тремя взаимно-перпендикулярными векторами , у которой площади граней-катетов равны — , и площадь грани-гипотенузы — . Тогда

Альтернативная формулировка: У четырехгранной пирамиды, у которой при одной из вершин все плоские углы прямые, сумма квадратов площадей боковых граней равна квадрату площади основания.

Разумеется, если обычная теорема Пифагора формулируется для длин сторон треугольников, то наша теорема формулируется для площадей сторон пирамиды. Доказать эту теорему в трех измерениях очень просто, если вы немного знаете векторную алгебру.

Доказательство

где .

Площадь представим как половину площади параллелограмма, построенного на векторах и

Как известно, векторное произведение двух векторов — это вектор, длина которого численно равна площади параллелограмма, построенного на этих векторах.
Поэтому

Что и требовалось доказать!

ЭВРИКА!

Моему восторгу не было границ! Я буквально прыгал от счастья. Конечно, это не бог весть какая сложная теорема, и доказательство очень простое, но ведь сам. И до меня — никто! Я был в этом искренне убежден в течение около года. Попытки найти хоть какие-то свидетельства о том, что это уже известно и доказано терпели неудачу одна за другой, и я думал, что совершил открытие. Это непредаваемое чувство! Я хотел поделиться этой теоремой со всем миром. Говорил о ней друзьям, знакомым математикам, просто знакомым с техническим/математическим образованием и без. Никто не разделял моего восторга и энтузиазма. Всем было попросту безразлично. Будто бы я не придумал и доказал теорему, а просто в магазин за хлебом сходил. Ну и что тут такого? Вот уж действительно… Как говорится, «Как скучно мы живём! В нас пропал дух авантюризма, мы перестали лазить в окна к любимым женщинам, мы перестали делать большие хорошие глупости.» (из фильма «Ирония судьбы»).

Конечно, как у человека, профессионально занимающегося исследованиями, подобное в моей жизни уже случалось, и не раз. Но этот момент был самым ярким и самым запоминающимся. Я испытал полную гамму чувств, эмоций, переживаний первооткрывателя. От зарождения мысли, кристализации идеи, нахождения доказательства — до полного непонимания и даже неприятия, которое встретили мои идеи у моих друзей, знакомых и, как мне тогда казалось, у целого мира. Это было уникально! Я словно почувствовал себя в шкуре Галлилея, Коперника, Ньютона, Шредингера, Бора, Эйнштейна и многих многих других открывателей.

Послесловие

В жизни, все оказалось гораздо проще и прозаичнее. Я опоздал… Но на сколько! Всего-то навсего 18 лет! Под страшными продолжительными пытками и не с первого раза Гугл признался мне, что эта теорема была опубликована в 1996 году!

Вот ссылка на статью:

Статья опубликована издательством Техасского технического университета. Авторы, профессиональные математики, ввели терминологию (которая, кстати, во многом совпала с моей) и доказали также и обобщенную теорему справедливую для пространства любой размерности большей единицы. Что же произойдет в размерностях более высоких, чем 3? Все очень просто: вместо граней и площадей будут гиперповерхности и многомерные объемы. А утверждение, конечно, останется все тем же: сумма квадратов объемов боковых граней равна квадрату объема основания, — просто количество граней будет больше, а объем каждой из них станет равен половине произведения векторов-образующих. Вообразить это почти невозможно! Можно только, как говорят философы, помыслить!

Что удивительно, узнав о том, что такая теорема уже известна, я ничуть не расстроился. Где-то в глубине души я подозревал, что вполне возможно, я был не первый, и понимал, что нужно быть всегда к этому готовым. Но тот эмоциониальный опыт, который я получил, зажег во мне искру исследователя, которая, я уверен, теперь уже не угаснет никогда!

Эрудированный читатель в комментариях прислал ссылку
Теорема де Гуа

Выдержка из Википедии

В 1783 году теорема была представлена Парижской академии наук французским математиком Ж.-П. де Гуа, однако ранее она была известна Рене Декарту[3] и до него Иоганну Фульгаберу (англ.), который, вероятно, первым открыл её в 1622 году[4]. В более общем виде теорему сформулировал Шарль Тинсо (фр.) в докладе Парижской академии наук в 1774 году[4]

Так что я опоздал не на 18 лет, а как минимум на пару веков!

Источники

Читатели указали в комментариях несколько полезных ссылок. Вот эти и некоторые другие ссылки:

Источник