Методы измерения информации
Как и любое физическое вещество информация имеет свои количественные характеристики. В современной информатике приняты следующие методы измерения информации:
Объемный метод измерения характеризуется количеством символов, содержащихся в конкретном сообщении. В вычислительной технике вся информация, независимо от ее природы (текст, число, изображение и т.д.), представляется в двоичной форме записи, т.е. состоящей из различных комбинаций двух символов 0 и 1. Один такой символ в вычислительной технике называется битом, совокупность восьми таких символов называется байтом, а большое количество символов, которыми оперирует ЭВМ, называется словом.
Энтропийный метод измерения информации используется в теории информации и кодирования. Он основывается на мере неопределенности появления некоторой совокупности событий и выражается вероятностью появления этих событий. Количество информации в сообщении при энтропийном методе оценки определяется тем, насколько уменьшается эта мера после получения сообщения. В теории информации используется следующая количественная мера:
где Э – энтропия;
m – число возможных равновероятных событий.
В случае, когда энтропия зависит не только от числа равновероятных событий выбора, но и от вероятности возможного выбора элемента информации К. Шеннон предложил следующую форму оценки энтропии:
где Рi – вероятность возможного выбора i-го элемента информации.
Тогда среднее количество информации при m числе выборке с вероятностью Рi каждой выборки определится выражением:
Алгоритмическая оценка информации характеризуется сложностью (размером) алгоритма (программы), которая позволяет ее произвести. На разных машинах и разных языках программирования такая оценка может быть разной. Поэтому задаются некоторой вычислительной машиной (например, элементарной машиной Тьюринга), а предлагаемая количественная оценка информации определяется сложностью слова, как минимальное число внутренних состояний машины, требуемой для его воспроизведения.
Структурная схема машины Тьюринга приведена на рисунке 2.2.
Рисунок 2.2 – Структурная схема машины Тьюринга
На рисунке 2.2 обозначено:
УУ – управляющее устройство;
СГ – считывающая головка;
Лента – источник информации бесконечная лента.
Управляющее устройство УУ определяет положение считывающей головки СГ <qi>. В каждой ячейке ленты записан символ <ai>. Таким образом, состояние машины <si> определится выражением:
Следующее перемещение ленты задается параметром <pi>. Тогда новое состояние машины определится следующим образом:
Таким образом, полное состояние машины Тьюринга можно задать, определив множества Q
Источник
Энтропийный способ
Количество информации
Существуют следующие способы измерения информации:
В теории информации и кодирования принят энтропийный или вероятностный подход к измерению информации. Количество информации – это числовая характеристика сигнала, которая отражает ту степень неопределенности (неполноту) знаний, которая исчезает после получения сообщения в виде данного сигнала. Меру неопределенности в теории информации называют энтропией, следовательно, метод называется энтропийным.
Неопределенность можно охарактеризовать количеством возможных выборов действий в конкретной ситуации, а полученную информацию величиной, на которую уменьшилась степень неопределенности. При полной информации выбора нет.
Пример 1. Необходимо найти дом, в котором на какой-то известной улице живет нужный человек. Информация о том, что номер дома четный уменьшит неопределенность в два раза.
Пример 2. Человек бросает монету и наблюдает какой стороной она упадет. Обе стороны монеты равноценны, поэтому вероятности того, что она упадет орлом или решкой одинаковы. Такой ситуации приписывается начальная неопределенность, характеризуемая двумя возможностями. Когда монета упадет, неопределенность равна 0.
Этот пример относится к группе событий, применительно к которым можно поставить вопрос типа «Да – Нет». Количество информации, которое можно получить при ответе на такой вопрос называется битом (binary digit).
Бит — это минимальная единица количества информации, т. к. получить информацию меньше одного бита нельзя. При получении информации в один бит неопределенность уменьшается в два раза. Таким образом, бросание монеты дает информацию 1 бит.
Пример 3. Рассмотрим систему из 2 электрических лампочек, которые независимо друг от друга могут быть включены или выключены. Такая система может иметь следующие состояния:
| Лампа А |
| Лампа В |
Чтобы получить информацию об этой системе, надо задать два вопроса: о лампочке А и о лампочке В., т. е. количество информации, содержащейся в этой системе I=2бита, а количество возможных состояний системы N=4.
Если взять 3 лампочки , то количество информации Iбудет равно 3бита, а количество возможных состояний системы N=8.
Связь между количеством информации и числом состояний системы устанавливается формулой Хартли
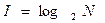
где N- количество возможных состояний системы (или количество равновероятных событий),
I – количество бит в сообщении о том, что такое событие произошло.
Ту же формулу можно записать

Если события не равновероятны, то количество бит в сообщении о том, что произошло данное событие будет равно
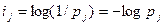
где 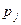
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Источник
Энтропийный способ измерения информации
Наука, изучающая количественные закономерности, связанные с получением, передачей, обработкой и хранением информации называется теорией информации.
Любое сообщение, с которыми мы имеем дело в теории информации, представляет собой совокупность сведений о некоторой физической системе. Очевидно, если бы состояние физической системы было известно заранее, не было бы смысла передавать сообщение, т.е. сообщение приобретает смысл тогда, когда состояние системы заранее неизвестно, случайно.
Поэтому в качестве объекта, о котором передается информация, мы будем рассматривать некоторую физическую систему, которая случайным образом может оказаться в том или ином состоянии, т.е. систему, которой заведомо присуща какая-то степень неопределенности.
Возникает вопрос: что значит «большая» или «меньшая» степень неопределенности и чем можно ее измерить?
Сравним между собой две системы, каждой из которых присуща некоторая неопределенность:
1) Монета, которая в результате бросания может оказаться в одном из двух состояний
2) Игральная кость, у которой 6 возможных состояний: 1, 2, 3, 4, 5, 6.
Неопределенность какой-то системы больше? Очевидно, второй, т.к. у нее больше возможных состояний, в каждом из которых система может оказаться с одинаковой вероятностью.
Может показаться, что степень неопределенности системы определяется числом возможных состояний системы. Но в общем случае это не так.
Рассмотрим, например, техническое устройство, которое может быть в двух состояниях: 1) исправно; 2) отказало.
Пусть до получения сведений (априори) вероятность исправной работы устройства 0,99, а вероятность отказа – 0,01.
Такая система обладает очень малой степенью неопределенности: почти наверняка можно сказать, что устройство будет работать исправно.
При бросании монеты тоже имеется 2 возможных состояния, но степень неопределенности гораздо больше.
Таким образом, степень неопределенности физической системы определяется не только числом ее возможных состояний, но и вероятностями состояний.
Перейдем к общему случаю.
Рассмотрим некоторую систему X, которая может принимать конечное множество состояний x1, x2, … xn с вероятностями p1, p2, … pn, где
xi) – вероятность того, что система X примет состояние xi. Очевидно, 
Запишем эти данные в виде таблицы
| xi | x1 | x2 | … | xn |
| pi | p1 | p2 | pn |
В качестве меры априорной неопределенности системы в теории информации применяется специальная характеристика, называемая энтропией.
Энтропией системы называется сумма произведений вероятностей различных состояний системы на логарифмы этих вероятностей, взятая с обратным знаком.
H(x)= – 
(знак «–» поставлен для того, чтобы энтропия была положительной; числа 0
Логарифм может быть взят при любом основании a>1. Перемена основания равносильна умножению энтропии на постоянное число, а выбор основания равносилен выбору определенной единицы измерения энтропии. Если за основание выбрано число 10, то говорят о «десятичных единицах» энтропии, если 2 – о «двоичных единицах».
На практике удобнее всего пользоваться логарифмами при основании 2 и измерять энтропию в двоичных единицах. Это хорошо согласуется с применяемой в компьютерах двоичной системой счисления.
Энтропия системы, которая имеет два равновозможных состояния (в качестве основания логарифма выберем 2) равна единице:
H(X)=
Определенная таким образом единица энтропии называется двоичной единицей и обозначается bit (от английского binary digit – двоичный знак)
Это энтропия одного разряда двоичного числа, если он с одинаковой вероятностью может быть нулем или единицей.
Энтропия системы X, которая имеет n равновероятных состояний, измеренная в двоичных единицах, определяется по формуле (1.2)
H(X)= 
H(X)= 
Т.е. энтропия системы с равновозможными состояниями равна логарифму числа состояний.
Например, для системы с восемью состояниями
H(X) =
Свойства энтропии [1]:
1) Энтропия обращается в ноль, когда одно из состояний системы достоверно, а другие невозможны (действительно, в этом случае все вероятности p1, p2, …, pn обращаются в нуль, кроме одной, например, pk, которая равна единице. pk logpk = 1×log1 = 0)
2) При заданном числе состояний энтропия обращается в максимум, когда эти состояния равновероятны. При увеличении числа состояний энтропия увеличивается.
3) Свойство аддитивности. Когда несколько независимых систем объединяются в одну, их энтропии складываются.
Энтропия и информация
Итак, мы определили энтропию как меру неопределенности состояния некоторой физической системы. Очевидно, что в результате получения сведений неопределенность системы может быть уменьшена. Чем больше объем полученных сведений, чем более содержательны сведения, тем больше информации о системе, тем менее неопределенным будет состояние системы.
Естественно поэтому количество информации измерять уменьшением энтропии той системы, для уточнения состояния которой предназначены сведения.
Рассмотрим некоторую системы Х, над которой производится наблюдение, и оценим информацию, получаемую в результате того, что состояние системы Х становится полностью известным. До получения информации энтропия системы была H(X). После получения сведений состояние системы полностью определилось, т.е. энтропия стала равной нулю.
Обозначим Ix информацию, получаемую в результате выяснения состояния системы Х. Она равна уменьшению энтропии:
Источник
Энтропийный способ измерения информации
Наука, изучающая количественные закономерности, связанные с получением, передачей, обработкой и хранением информации называется теорией информации.
Любое сообщение, с которыми мы имеем дело в теории информации, представляет собой совокупность сведений о некоторой физической системе. Очевидно, если бы состояние физической системы было известно заранее, не было бы смысла передавать сообщение, т.е. сообщение приобретает смысл тогда, когда состояние системы заранее неизвестно, случайно.
Поэтому в качестве объекта, о котором передается информация, мы будем рассматривать некоторую физическую систему, которая случайным образом может оказаться в том или ином состоянии, т.е. систему, которой заведомо присуща какая-то степень неопределенности.
Возникает вопрос: что значит «большая» или «меньшая» степень неопределенности и чем можно ее измерить?
Сравним между собой две системы, каждой из которых присуща некоторая неопределенность:
1) Монета, которая в результате бросания может оказаться в одном из двух состояний
2) Игральная кость, у которой 6 возможных состояний: 1, 2, 3, 4, 5, 6.
Неопределенность какой-то системы больше? Очевидно, второй, т.к. у нее больше возможных состояний, в каждом из которых система может оказаться с одинаковой вероятностью.
Может показаться, что степень неопределенности системы определяется числом возможных состояний системы. Но в общем случае это не так.
Рассмотрим, например, техническое устройство, которое может быть в двух состояниях: 1) исправно; 2) отказало.
Пусть до получения сведений (априори) вероятность исправной работы устройства 0,99, а вероятность отказа – 0,01.
Такая система обладает очень малой степенью неопределенности: почти наверняка можно сказать, что устройство будет работать исправно.
При бросании монеты тоже имеется 2 возможных состояния, но степень неопределенности гораздо больше.
Таким образом, степень неопределенности физической системы определяется не только числом ее возможных состояний, но и вероятностями состояний.
Перейдем к общему случаю.
Рассмотрим некоторую систему X, которая может принимать конечное множество состояний x1, x2, … xn с вероятностями p1, p2, … pn, где
xi) – вероятность того, что система X примет состояние xi. Очевидно, 
Запишем эти данные в виде таблицы
| xi | x1 | x2 | … | xn |
| pi | p1 | p2 | pn |
В качестве меры априорной неопределенности системы в теории информации применяется специальная характеристика, называемая энтропией.
Энтропией системы называется сумма произведений вероятностей различных состояний системы на логарифмы этих вероятностей, взятая с обратным знаком.
H(x)= – 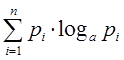
(знак «–» поставлен для того, чтобы энтропия была положительной; числа 0
Логарифм может быть взят при любом основании a>1. Перемена основания равносильна умножению энтропии на постоянное число, а выбор основания равносилен выбору определенной единицы измерения энтропии. Если за основание выбрано число 10, то говорят о «десятичных единицах» энтропии, если 2 – о «двоичных единицах».
На практике удобнее всего пользоваться логарифмами при основании 2 и измерять энтропию в двоичных единицах. Это хорошо согласуется с применяемой в компьютерах двоичной системой счисления.
Энтропия системы, которая имеет два равновозможных состояния (в качестве основания логарифма выберем 2) равна единице:
H(X)=
Определенная таким образом единица энтропии называется двоичной единицей и обозначается bit (от английского binary digit – двоичный знак)
Это энтропия одного разряда двоичного числа, если он с одинаковой вероятностью может быть нулем или единицей.
Энтропия системы X, которая имеет n равновероятных состояний, измеренная в двоичных единицах, определяется по формуле (1.2)
H(X)= 
H(X)= 
Т.е. энтропия системы с равновозможными состояниями равна логарифму числа состояний.
Например, для системы с восемью состояниями
H(X) =
Свойства энтропии [1]:
1) Энтропия обращается в ноль, когда одно из состояний системы достоверно, а другие невозможны (действительно, в этом случае все вероятности p1, p2, …, pn обращаются в нуль, кроме одной, например, pk, которая равна единице. pk logpk = 1×log1 = 0)
2) При заданном числе состояний энтропия обращается в максимум, когда эти состояния равновероятны. При увеличении числа состояний энтропия увеличивается.
3) Свойство аддитивности. Когда несколько независимых систем объединяются в одну, их энтропии складываются.
Энтропия и информация
Итак, мы определили энтропию как меру неопределенности состояния некоторой физической системы. Очевидно, что в результате получения сведений неопределенность системы может быть уменьшена. Чем больше объем полученных сведений, чем более содержательны сведения, тем больше информации о системе, тем менее неопределенным будет состояние системы.
Естественно поэтому количество информации измерять уменьшением энтропии той системы, для уточнения состояния которой предназначены сведения.
Рассмотрим некоторую системы Х, над которой производится наблюдение, и оценим информацию, получаемую в результате того, что состояние системы Х становится полностью известным. До получения информации энтропия системы была H(X). После получения сведений состояние системы полностью определилось, т.е. энтропия стала равной нулю.
Обозначим Ix информацию, получаемую в результате выяснения состояния системы Х. Она равна уменьшению энтропии:
Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций.
Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим.
Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ — конструкции, предназначенные для поддерживания проводов на необходимой высоте над землей, водой.
Источник














