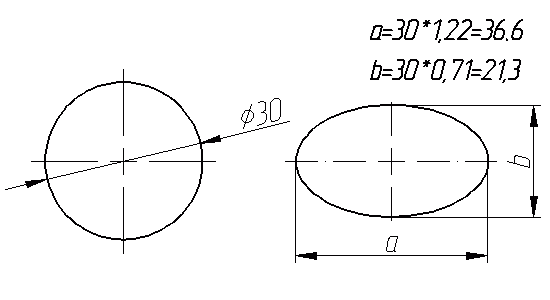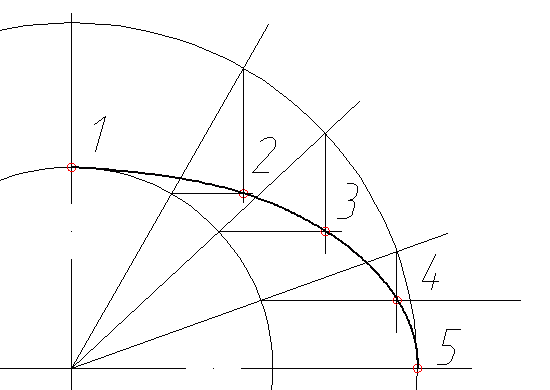Эллипс построение графическим способом
Построение эллипса с помощью циркуля. Как начертить эллипс?
Эллипс — геометрическая фигура. В математике имеет весьма занимательные свойства. Но наша задача не рассчитывать фокальные расстояния, а уметь построить эллипс на чертеже. В курсе инженерной графики эллипсы встречаются наиболее часто в трех случаях:
-сечение конуса плоскостью пересекающей ось конуса,
-сечение циллиндра наклонной плоскостью
-изображение окружностей в аксонометрических проекциях (построение изометрической проекции или диметрической проекции)
Если начертить эллипс малого размера от руки и на глаз еще не так сложно, то при необходимости построить эллипс с осями к примеру более 50-60 мм используется специальная методика построения эллипсов — это значительно влияет на конечную красоту чертежа, а остатки построений на нем добавят вам небольшой плюс в глазах преподавателя, даже если он попросит вас их потом стереть. Строго говоря, методик построения эллипсов несколько. Мы рассмотрим только одну из них.
Чтобы не быть совсем абстрактным, я предлагаю начертить эллипс, являющийся отображением окружности в изометрии. Заодно вспомним коэффициенты искажения. Итак, возьмем окружность диаметром 30мм. Такая окружность в изометрии будет иметь вид эллипса с осями 36,6мм и 21,3 мм.
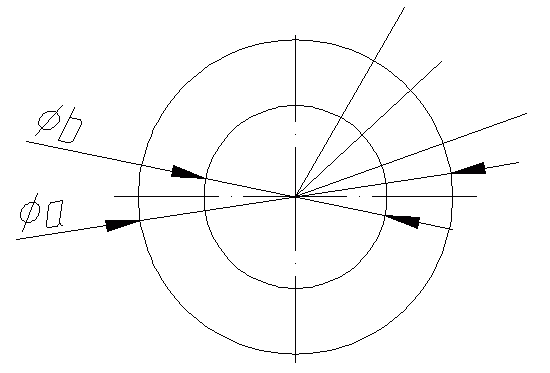
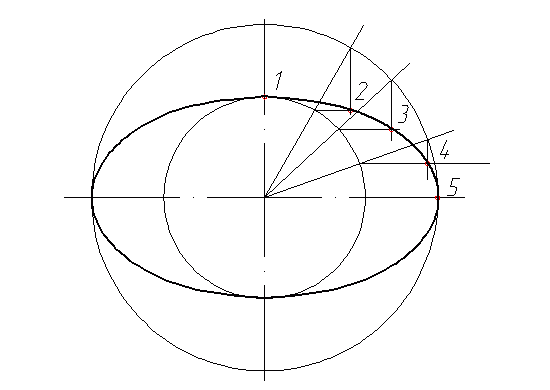
Начнем построение эллипса. На первом этапе необходимо из центра эллипса провести две вспомогательные окружности, диаметры которых будут равны большой и малой оси эллипса. Затем, из центра проведем несколько лучей, так чтоб они пересекали обе окружности. Для удобства отображения я буду рассматривать одну четверть. Количество вспомогательных лучей зависит исключительно от желаемой точности построений и размеров эллипса, в нашем случае это будут 3 луча (рекомендую такое количество лучей для эллипсов с большой осью от 60 и где-то до 120 мм)
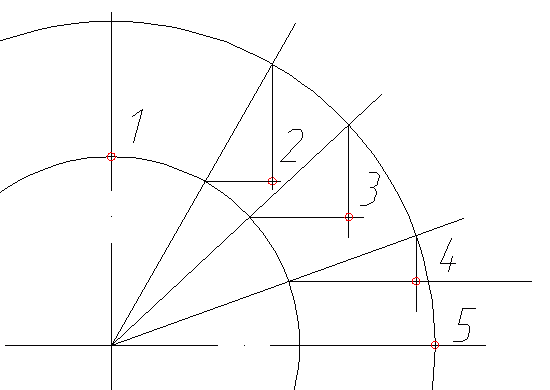
На следующем шаге мы получим дополнительные точки эллипса. Для этого, мы поочередно сделаем с каждым лучем следующее: из точки пересечения луча с малой окружностью проведем горизонтальную линию в сторону большой окружности, а из точки пересечения луча с большой окружостью проведем линию до пересечения с только что начерченной горизонталью. Таким образом мы получим точки 2, 3 и 4. Точки 1 и 5 так же принадлежат эллипсу.
Теперь, имея пять точек мы без труда проведем через них кривую. Обратите внимание, что в точке пересечения с осями кривая эллипса строго перпендикулярна им.
Нам осталось лишь достроить оставшиеся три четверти фигуры. Я рекомендую вам не производить аналогичные построения, а аккуратно перенести\отразить точки 2, 3, 4 через оси. Но конечно же, можно и повторить предыдущие шаги для закрепления навыка.
На этом построение эллипса заканчивается. Надеюсь, что нам удалось достаточно подробно и понятно изложить материал, и построить эллипс для вас теперь сущий пустяк. Желаю вам успехов в учебе! Если же что-то катастрофически не получается, или совсем нет времени и сил — вы всегда можете обратиться к нам за помощью в оформлении чертежей.
Вы можете сказать «спасибо!» автору статьи:
пройдите по любой из рекламных ссылок в левой колонке, этим вы поддержите проект «White Bird. Чертежи Студентам»
или запишите наш телефон и расскажите о нас своим друзьям — кто-то наверняка ищет способ выполнить чертежи
или создайте у себя на страничке или в блоге заметку про наши уроки — и кто-то еще сможет освоить черчение.
А вот это — не реклама. Это напоминание, что каждый из нас может сделать. Если хотите — это просьба. Мы действительно им нужны: 
Автор комментария: Рустам
Дата: 2011-03-22
Автор комментария: закир
Дата: 2011-05-19
огромное спасибо оч выручили.
Автор комментария: Вова
Дата: 2011-12-15
Автор комментария: Богдан Тарасюк
Дата: 2012-01-13
Автор комментария: ваня
Дата: 2012-01-24
Автор комментария: Виталий
Дата: 2012-05-13
Автор комментария: Леон
Дата: 2012-05-25
Благодарю! Все очень понятно обьяснили.
Автор комментария: антон
Дата: 2012-05-31
спасибо черчу через компас по вашим примерам вроде получается
Автор комментария: Влад
Дата: 2012-10-08
спасибо большое! все понятно. очень помогло
Автор комментария: Илья
Дата: 2012-10-09
но есть же способ проще. просто я его призабыл за пол года поэтому и зашел сюда
Точно, вы правы! Именно поэтому по тексту написано, что есть несколько способов, и мы рассмотрим один из них. Отмечу, что приведенный здесь способ (при достаточном количестве точек) дает максимальную точность построения.
Автор комментария: Женя
Дата: 2012-10-14
Спасибо. Очень помогло!
Автор комментария: Витя
Дата: 2012-10-22
Автор комментария: Нкитка
Дата: 2012-10-26
тупой способ циркулем намного проще и быстрей
А никто и не претендует — всего лишь один из способов. Все зависит от того, какую точность нужно достичь. Я к примеру вообще предпочитаю в САПровских системах чертить. А вы? 🙂
Автор комментария: Татьяна
Дата: 2012-11-04
Автор комментария: Владимир
Дата: 2012-11-24
Спасибо в ремонте очень пригодилось!
Автор комментария: Светлана
Дата: 2012-12-17
Огромное спасибо!Все просто и доступно!
Благодарю за отзыв, Светлана! Слова такого плана меня всегда наводят на мысль: а почему те люди, которые получают от нашего государства деньги за написание методических пособий, делают это не просто, не понятно, и не доступно? Очень надеюсь, что они это не специально
Автор комментария: Женя
Дата: 2013-01-21
а точки от руки соединять? как-то у меня не очень ровно получается.
Тут дело такое. В идеале — после определения некоторого количества точек хорошо было бы соединить их по лекалу. Но я уверен, что для вас такой вариант не станет облегчением, поскольку я не помню, чтоб где-то кого-то учили работать с лекальными линейками. Однако, если они есть под рукой — можете попробовать. Возможно вам удастся подобрать верные кривые. Ну а если нет — то просто старайтесь поаккуратнее соединить от руки. Либо можно увеличить количество вспомогательных точек (после чего возненавидеть построение эллипсов 🙂 ) Главное — не опускайте рук!
Автор комментария: ДАНИИЛ
Дата: 2013-01-21
СЕРДЧЕЧНАЯ БЛАГОДАРНОСТЬ ЗА ВАШ ТРУД
sposibo ochen pomoglo
Автор комментария: рома
Дата: 2013-03-12
Великолепно!) спасибо большое!)
Автор комментария: Анатолий.
Дата: 2013-07-07
Спасибо! Очень понятно и доступно расказано о построение элипса. С геометрией у меня все в порядке, а вот элипсы строить не доводилось. По Вашей методике постою элипс на потолке, теперь точно получится! Спасибо еще раз.
Автор комментария: Павел
Дата: 2013-07-09
Спасибо огромное всен очень понятно объяснено!
Автор комментария: Андраник
Дата: 2013-07-18
Большое спасибо! Выручил.
Автор комментария: Владислав
Дата: 2013-09-04
Спасибо! Потребовалось прорезать точное отверстие под круглый дымоход в наклонной плоскости, Ваш метод построения эллипса очень помог!
Автор комментария: фариза
Дата: 2014-01-09
так просто,только есть один вопрос,можете сказать расстояний между точками (1,2,3,4,5)
Автор комментария: 999
Дата: 2014-02-16
«Теперь, имея пять точек мы без труда проведем через них кривую» Они что издеваются?!
Автор комментария: сережа
Дата: 2014-03-06
как начертить машину в компасе
Автор комментария: Александр
Дата: 2014-03-11
Здравствуйте!Помогите рассчитать половинку элипса или половинку овала .Где длина равна а-4800мм а ширина половинки овала равна b-500мм.Спасибо
Автор комментария: Андрей
Дата: 2014-05-03
Благодарен всё ясно, просто и понятно.
Автор комментария: Светлана
Дата: 2014-05-17
Автор комментария: Majid Shabanov
Дата: 2014-06-17
Большое спасибо! Очень доступном виде обьяснили, без лищных слов.
Автор комментария: arhitektor stroitel
Дата: 2014-07-06
http://oval.ing-grafika.ru/1.html 2 способ посмотрите.Он удобнее вроде.
Автор комментария: Альбина
Дата: 2014-09-28
Cпасибо! Очень доступно изложено) Здорово получилось)))
Автор комментария: наталья
Дата: 2014-10-12
огромное Вам спасибо
Автор комментария: алик
Дата: 2014-11-25
Большое человеческое СПАСИБО
Автор комментария: Юля
Дата: 2014-12-10
Автор комментария: Александр
Дата: 2015-01-06
Принцип построения изложен предельно понятно. Однако, не изложено объяснение того, что в результате проведенных операций должен получиться именно эллипс, а не овал. Я понимаю, что принцип построения эллипса правильный, но нет объяснения почему.
Автор комментария: Роман
Дата: 2015-03-02
Спасибо! Реально доступно объяснили! Очень помогло.
Автор комментария: Міша
Дата: 2015-03-03
Дуже дякую виручили, дуже допомогло)))) +1
Автор комментария: Илья
Дата: 2015-03-19
По поводу «тупой способ циркулем намного проще и быстрей». Это как?
Автор комментария: :O
Дата: 2015-11-25
Черт.. Это так просто!
Автор комментария: Елизавета
Дата: 2016-02-04
СПАСИБО! не была на паре, задали дома по определенным размерам начертить, просто спасли!
Ну вот и замечательно 🙂 Эх, все никак не удается мне подготовить продолжение — еще один-два способа разобрать
Автор комментария: j
Дата: 2016-10-22
Автор комментария: Владимир
Дата: 2017-01-10
Всё просто, спасибо за комментарии.
Автор комментария: Рустем
Дата: 2017-04-17
Автор комментария: Володя
Дата: 2018-01-17
У вас уже заданны большой и малый диаметры зллипса, прошу к данному варианту добавить метод засечек исходя только из данных диаметра круга. С.У.Стенин.
Автор комментария: Александр
Дата: 2018-02-02
Великолепно. просто,доходчиво и без лишней информации!!
Автор комментария: Дамир
Дата: 2018-04-03
Автор комментария: саня
Дата: 2018-06-13
Попробуйте еще. Судя по остальным отзывам — способ «ну очень рабочий!»
Источник
Кривые второго порядка — определение и построение с примерами решения
Содержание:
Геометрической фигурой или просто фигурой на плоскости называется множество точек. Задать фигуру — значит указать, из каких точек плоскости она состоит. Одним из важных способов задания фигуры на плоскости является ее задание при помощи уравнений с двумя неизвестными. Произвольное уравнение с двумя неизвестными х и у записывается в виде 
- Если точка М(а,Ь) принадлежит фигуре Ф, то координаты (а,Ь) являются решениями уравнения
- если пара чисел (c,d) является решением уравнения F(x,y) = 0, то точка N(c,d) принадлежит фигуре Ф.
Это определение в более компактной записи выглядит следующим образом. Уравнение называется уравнением фигуры, если 
, то есть (а, b) — решение уравнения F(x,y) = 0.
Из определения уравнения фигуры следует, что фигура Ф состоит только из тех точек плоскости, координаты которых являются решениями уравнения , т.е. уравнение фигуры задает эту фигуру.
Возможны два вида задач:
- дано уравнение и надо построить фигуру Ф, уравнением которой является ;
- дана фигура Ф и надо найти уравнение этой фигуры.
Первая задача сводится к построению графика уравнения и решается, чаще всего, методами математического анализа.
Для решения второй задачи, как следует из определения уравнения фигуры, достаточно:
- Задать фигуру геометрически, т.е. сформулировать условие, которому удовлетворяют только точки фигуры (довольно часто определение фигуры содержит такое условие);
- Записать в координатах условие, сформулированное в первом пункте.
Эллипс
Эллипсом называется линия, состоящая из всех точек плоскости, для каждой из которых сумма расстояний до двух данных точек 
, есть величина постоянная (большая, чем расстояние между 
).
Точки 
называются фокусами эллипса. Обозначив расстояние между фокусами через 2с, а сумму расстояний от точек эллипса до фокусов через 2а, имеем с b. В этом случае а называется большой полуосью, a b — малой.
Если а =Ь, то уравнение (7.3) можно переписать в виде:
(7.5)
Это уравнение окружности с центром в начале координат. Эллипс (3) можно получить из окружности (4) сжатием плоскости к оси Ох. Пусть на плоскости выбрана прямоугольная система координат Оху. Тогда преобразование, переводящее произвольную точку М(х,у) в точку 
координаты которой задаются формулами 
будет окружность (4) переводить в эллипс, заданный соотношением 
Число 
называется эксцентриситетом эллипса. Эксцентриситет 
характеризует форму эллипса: чем ближе к нулю, тем больше эллипс похож на окружность; при увеличении 
становится более вытянутым
Фокальными радиусами точки М эллипса называются отрезки прямых, соединяющие эту точку с фокусами 
. Их длины 
и 
задаются формулами 
Прямые 
называются директрисами эллипса. Директриса 
называется левой, а 
— правой. Так как для эллипса 
и, следовательно, левая директриса располагается левее левой вершины эллипса, а правая — правее правой вершины.
Директрисы обладают следующим свойством: отношение расстояния г любой точки эллипса от фокуса к ее расстоянию d до соответствующей директрисы есть величина постоянная, равная эксцентриситету, т.е. 
Гипербола
Гиперболой называется линия, состоящая из всех точек плоскости, модуль разности расстояний от которых до двух данных точек 
есть величина постоянная (не равная нулю и меньшая, чем расстояние между 
).
Точки 
называются фокусами гиперболы. Пусть по-прежнему расстояние между фокусами равно 2с. Модуль расстояний от точек гиперболы до фокусов 
обозначим через а. По условию, а 0) (рис. 9.7). Ось абсцисс проведём через фокус F перпендикулярно директрисе. Начало координат расположим посередине между фокусом и директрисой. Пусть А — произвольная точка плоскости с координатами (х, у) и пусть 
. Тогда точка А будет лежать на параболе, если r=d, где d- расстояние от точки А до директрисы. Фокус F имеет координаты 
.
Тогда 
А расстояние 
Подставив в формулу r=d, будем иметь
. Возведя обе части равенства в квадрат, получим
или
(9.4.1)
Уравнение (9.4.1)- каноническое уравнение параболы. Уравнения 
также определяют параболы.
Легко показать, что уравнение 
, определяет параболу, ось симметрии которой перпендикулярна оси абсцисс; эта парабола будет восходящей, если а > 0 и нисходящей, если а 
О. Для этого выделим полный квадрат:
и сделаем параллельный перенос по формулам
В новых координатах преобразуемое уравнение примет вид: 
где р — положительное число, определяется равенством 
.
Пример:
Пусть заданы точка F и прямая у =-1 (рис. 9.8). Множество точек Р(х, y) для которых расстояние |PF| равно расстоянию
, называется параболой. Прямая у = -1 называется директрисой параболы, а точка F — фокусом параболы. Чтобы выяснить, как располагаются точки Р, удовлетворяющие условию
, запишем это равенство с помощью координат: 
, или после упрощения 
. Это уравнение геометрического места точек, образующих параболу (рис. 9.8).
Кривые второго порядка на плоскости
Кривой второго порядка называется фигура на плоскости, задаваемая в прямоугольной системе координат уравнением второй степени относительно переменных х и у:
где коэффициенты А, В и С не равны одновременно нулю 
Любая кривая второго порядка на плоскости принадлежит к одному из типов: эллипс, гипербола, парабола, две пересекающиеся прямые, 2 параллельные прямые, прямая, точка, пустое множество.
Кривая второго порядка принадлежит эллиптическому типу, если коэффициент В равен нулю: В=0, а коэффициенты А и С имеют одинаковые знаки: АС>0.
Кривая второго порядка принадлежит гиперболическому типу, если коэффициент В равен нулю: В=0, а коэффициенты А и С имеют противоположные знаки: АС 2с. Точка М(х,у) принадлежит эллипсу тогда и только тогда, когда ее координаты удовлетворяют уравнению
которое называют каноническим уравнением эллипса.
Число а называют большей полуосью эллипса, число 
— мень-
шей полуосью эллипса, 2а и 2b — соответственно большей и меньшей осями эллипса. Точки 
называют вершинами эллипса, а 
— его фокусами (рис. 12).
Координатные оси являются осями симметрии эллипса, а начало координат — его центром симметрии. Центр симметрии эллипса называется центром эллипса.
Замечание. Каноническое уравнение эллипса можно рассматривать и в случае b>а. Оно определяет эллипс с большей полуосью b, фокусы которого лежат на оси Оу.
В случае а=b каноническое уравнение эллипса принимает вид 
и определяет окружность радиуса а с центром в начале координат.
Эксцентриситетом эллипса называется отношение фокусного расстояния к длине большей оси.
Так, в случае а>b эксцентриситет эллипса выражается формулой:
Эксцентриситет изменяется от нуля до единицы 
и характеризует форму эллипса. Для окружности 
Чем больше эксцентриситет, тем более вытянут эллипс.
Пример:
Показать, что уравнение
является уравнением эллипса. Найти его центр, полуоси, вершины, фокусы и эксцентриситет. Построить кривую.
Решение:
Дополняя члены, содержащие х и у соответственно, до полных квадратов, приведем данное уравнение к каноническому виду:
— каноническое уравнение эллипса с центром в точке 
большей полуосью а=3 и меньшей полуосью 
Найдем эксцентриситет эллипса:
Для вычисления вершин и фокусов удобно пользовать новой прямоугольной системой координат, начало которой находится в точке 
а оси 
параллельны соответственно осям Ох, Оу и имеют те же направления (осуществили преобразование параллельного переноса). Тогда новые координаты точки будут равны ее старым координатам минус старые координаты нового начала, т.е. 
В новой системе координат координаты 
вершин и фокусов гиперболы будут следующими:
Переходя к старым координатам, получим:
Построим график эллипса.
Задача решена.
Гиперболой называется множество всех точек плоскости, для которых модуль разности расстояний до двух данных точек, называемых фокусами, есть величина постоянная, меньшая расстояния между фокусами.
Так же, как и для эллипса, геометрическое свойство точек гиперболы выразим аналитически. Расстояние между фокусами назовем фокусным расстоянием и обозначим через 2с. Постоянную величину обозначим через 2а: 2а
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Источник
