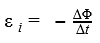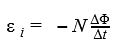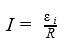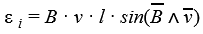Электромагнитная индукция способы получения индукционного тока

В 1831 г. Майкл Фарадей открыл, что во всяком замкнутом проводящем контуре при изменении потока магнитной индукции через поверхность, ограниченную этим контуром, возникает электрический ток. Это явление называют электромагнитной индукцией , а возникающий ток — индукционным .

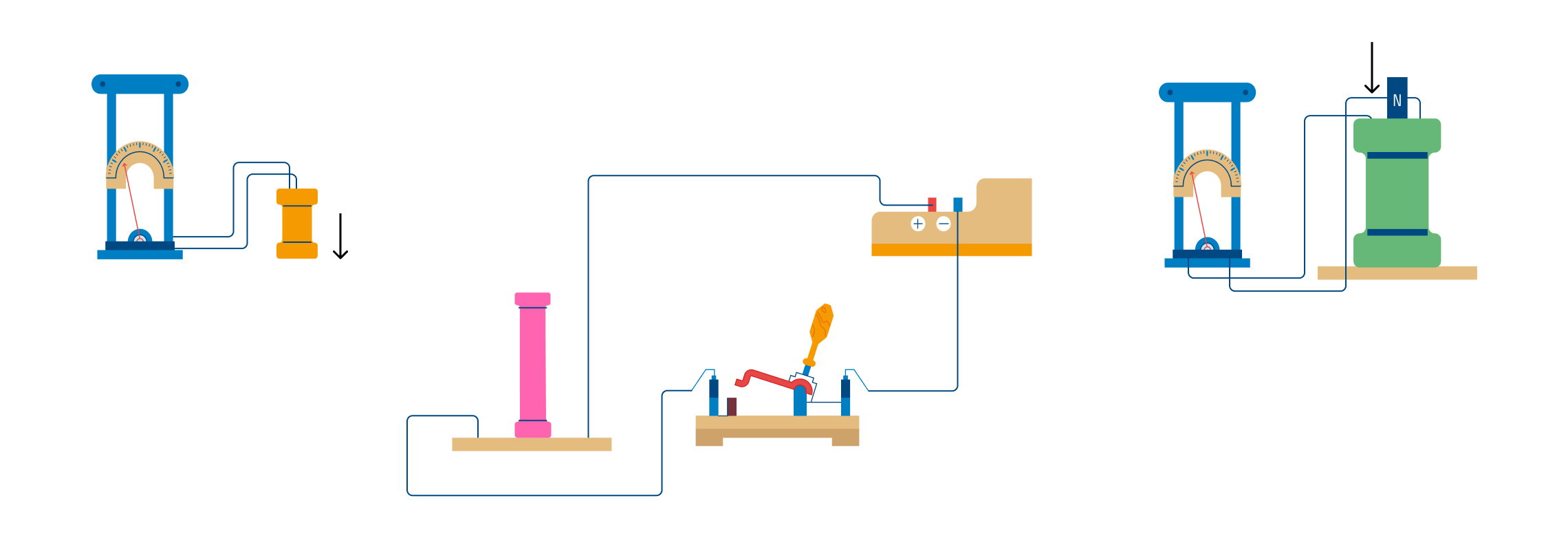
Величина индукционного тока не зависит от способа, которым вызывается изменение потока магнитной индукции Φ, и определяется только скоростью изменения магнитного потока . При изменении знака направление индукционного тока изменяется на противоположное. Рассмотрим эксперимент на Рис. 3.8.1.

Рис. 3.8.1. Наблюдение электромагнитной индукции

Силу тока i₁ в контуре 1 можно менять, благодаря чему будет меняться создаваемое им магнитное поле, пронизывающее контур 2. Если увеличивать ток i₁, поток магнитной индукции Φ через контур 2 будет расти. Это приведет к появлению в контуре 2 индукционного тока i₂. Уменьшение i₁, напротив, вызовет уменьшение потока магнитной индукции Φ через контур 2, что приведет к появлению в нем индукционного тока i₂ другого направления.

Индукционный ток i₂ можно вызвать также, приближая контур 2 к контуру 1, или удаляя его от первого. В этих двух случаях направления токов i₂ будут противоположными. Очевидно, аналогичных результатов можно достичь, если приближать контур 1 к контуру 2, или удаляя его от второго.

Наконец, электромагнитную индукцию можно вызвать, не перемещая контур 2 поступательно, а поворачивая его так, чтобы менялся угол между нормалями к контурам.

Заполнение всего пространства, в котором поле отлично от нуля, однородным пара- или ферромагнетиком приводит к увеличению индукционного тока в μ раз.

Э.Х. Ленц установил правило, с помощью которого можно найти направление индукционного тока: индукционный ток всегда направлен так, чтобы противодействовать причине, его вызывающей . Пусть, например, контур 2 неподвижен, а ток индуктируется в нем путем изменения тока в первом контуре. В этом случае возникает ток i₂ такого направления, что созданный им магнитный поток стремится ослабить изменения внешнего потока, которые и вызвали появление индукционного тока. С точки зрения механической аналогии, картина аналогична растяжению пружины.

3.8.2. Электродвижущая сила индукции

Для создания тока в цепи необходимо наличие ЭДС. Опыты Фарадея свидетельствуют о том, что при изменении магнитного потока в контуре возникает электродвижущая сила индукции ε_i. Рассмотрим контур, участок которого 1 — 2 длиной l может перемещаться без нарушения контакта с остальной частью контура (Рис. 3.8.1). Пусть на контур действует однородное магнитное поле, перпендикулярное плоскости чертежа. Приведем подвижную часть контура 1 — 2 в движение со скоростью . С той же скоростью будут перемещаться относительно поля и носители заряда в проводнике — электроны. На каждый электрон действует сила Лоренца, равная по модулю величине:

(3.8.1)

(индекс «||» указывает на то, что сила направлена вдоль провода).

Действие этой силы эквивалентно действию некоторой силы с напряженностью поля:

(3.8.2)

Это поле неэлектростатического происхождения направлено так, как показано на Рис. 3.8.2.

Рис. 3.8.2. К выводу закона Фарадея

Вычислив циркуляцию этого поля по контуру, получим ЭДС, действующую в контуре:

(3.8.3)

где dS = lvdt — приращение площади контура за время dt.

При вычислении циркуляции учтено, что Е_l отлична от нуля лишь на участке l, причем на этом участке всюду Е = Е_l.

Произведение ВdS = dΦ, следовательно, ЭДС индукции, возникающая в замкнутом контуре, равна скорости изменения магнитного потока Φ, пронизывающего контур:

(3.8.4)

Формула (3.8.4) определяет закон электромагнитной индукции Фарадея. Знак «минус» в (3.8.4) соответствует правилу Ленца.

Единицей магнитного потока в СИ является 1 Вб, который представляет собой поток через поверхность в 1 м&sup2, пересекаемую нормальными к ней линиями магнитного поля с индукцией в 1 Тл. При скорости изменения потока 1 Вб/с в контуре индуцируется ЭДС в 1 В.

Пусть контур, в котором индуцируется ЭДС, состоит не из одного, а из N одинаковых витков, т.е. представляет собой соленоид. Поскольку витки соленоида соединены последовательно, общая ЭДС равна сумме ЭДС, индуцируемых в каждом из витков отдельно:

(3.8.5)

Эту величину называют потокосцеплением (полным магнитным потоком) . Если поток, пронизывающий каждый из витков, одинаков, то:

(3.8.6)

(3.8.7)

Используя (3.8.5), для соленоида имеем:

(3.8.8)

Рассмотрим, например, катушку, имеющую N витков и вращающуюся в однородном постоянном магнитном поле с постоянной скоростью ω (Рис. 3.8.3).

Рис. 3.8.3. Катушка, вращающаяся в магнитном поле

Найдем ЭДС индукции. Поток через один виток равен:

(3.8.9)

Полный поток равен:

(3.8.10)

Угол α меняется со временем по закону α = ωt, следовательно:

(3.8.11)

Используя формулу (3.8.8), получим:

(3.8.12)

где ε_m = ωNBS — амплитуда (максимальное значение) величины ЭДС.

Cледовательно, в катушке индуктируется переменная ЭДС, изменяющаяся со временем по гармоническому закону.

3.8.3. Токи Фуко

Индукционные токи могут возбуждаться не только в контурах, но и в сплошных массивных проводниках. В этом случае они называются токами Фуко (вихревыми токами) . Поскольку электрическое сопротивление массивного проводника мало, вихревые токи могут достигать большой силы.

Токи Фуко подчиняются правилу Ленца — они выбирают внутри проводника такие пути, чтобы своим действием в наибольшей мере противодействовать причине, их породившей. Поэтому движущиеся в сильном магнитном поле хорошие проводники испытывают сильное торможение. Этим обстоятельством пользуются для успокоения (демпфирования) подвижных частей гальванометров, сейсмографов и других приборов. На подвижной части прибора устанавливается проводящая (например, алюминиевая) пластинка в виде сектора, который входит в зазор между полюсами сильного постоянного магнита (Рис. 3.8.4).

Рис. 3.8.4. Электромагнитный успокоитель

При движении пластинки в ней возникают вихревые токи, вызывающие торможение системы (механическая аналогия — движение маятника в вязкой среде). Преимущество такого способа состоит в том, что торможение возникает только при движении пластинки и отсутствует, когда пластика неподвижна. Поэтому электромагнитный успокоитель совершенно не препятствует точному приходу системы в положение равновесия.

Тепловое действие токов Фуко применяется в индукционных печах. В такой печи имеется катушка, через которую протекает высокочастотный ток большой силы. Если внутри катушки поместить проводящее тело, в нем возникнут интенсивные вихревые токи, которые разогревают это тело до температуры плавления. Таким способом плавят металлы в вакууме, что позволяет получать химически чистые материалы.

Во многих случаях токи Фуко вызывают нежелательные последствия. Поэтому, например, чтобы предотвратить потери на нагревание вихревыми токами сердечников трансформаторов, такие сердечники делают из тонких пластинок, разделенных изолирующими прослойками. Пластики располагаются так, чтобы возможные направления токов Фуко были бы перпендикулярны к их поверхностям.

3.8.4. Явление самоиндукции

Электрический ток i, текущий в любом контуре, создает пронизывающий этот контур магнитный поток Ψ. При изменении тока будет изменяться и магнитный поток Ψ, следовательно, в контуре будет индуцироваться ЭДС. Это явление называется самоиндукцией .

В соответствии с законом Био-Савара-Лапласа магнитная индукция В пропорциональна силе тока, вызвавшего поле. Отсюда следует, что ток в контуре и создаваемый им полный магнитный поток через контур Ψ должны быть пропорциональны:

(3.8.13)

Коэффициент пропорциональности L в (3.8.13) называется индуктивностью контура . При неизменной силе тока полный магнитный поток через контур Ψ может изменяться за счет изменения формы и размеров контура, а также от магнитных свойств среды. Поэтому индуктивность зависит от геометрии контура и от магнитных свойств материала, находящегося внутри контура или соленоида (сердечника).

За единицу индуктивности в СИ принимают 1 Гн — индуктивность такого проводника, у которого при силе тока в 1 А возникает полный магнитный поток в 1 Вб.

Вычислим индуктивность соленоида. Магнитная индукция внутри длинного соленоида при протекании через него тока i равна:

(3.8.14)

где n — число витков, приходящееся на единицу длины соленоида.

Полный магнитный поток соленоида Ψ c N витками равен:

(3.8.15)

где l — длина соленоида, S — площадь его поперечного сечения.

Сравнивая (3.8.15) и (3.8.13), получаем выражение для индуктивности длинного соленоида:

(3.8.16)

где V — объем соленоида.

При изменении магнитного потока возникает ЭДС самоиндукции:

(3.8.17)

Если индуктивность остается постоянной при изменении силы тока, то ЭДС самоиндукции имеет вид:

(3.8.18)

Наверх

Источник

Закон электромагнитной индукции

О чем эта статья:

11 класс, ЕГЭ/ОГЭ

Магнитный поток

Прежде, чем разобраться с тем, что такое электромагнитная индукция, нужно определить такую сущность, как магнитный поток.

Представьте, что вы взяли обруч в руки и вышли на улицу в ливень. Чем сильнее ливень, тем больше через этот обруч пройдет воды — поток воды больше.

Если обруч расположен горизонтально, то через него пройдет много воды. А если начать его поворачивать — уже меньше, потому что он расположен не под прямым углом к вертикали.

Теперь давайте поставим обруч вертикально — ни одной капли не пройдет сквозь него (если ветер не подует, конечно).

Магнитный поток по сути своей — это тот же самый поток воды через обруч, только считаем мы величину прошедшего через площадь магнитного поля, а не дождя.

Магнитным потоком через площадь S контура называют скалярную физическую величину, равную произведению модуля вектора магнитной индукции B, площади поверхности S, пронизываемой данным потоком, и косинуса угла α между направлением вектора магнитной индукции и вектора нормали (перпендикуляра к плоскости данной поверхности):

Магнитный поток

Ф — магнитный поток [Вб]

B — магнитная индукция [Тл]

S — площадь пронизываемой поверхности [м^2]

n — вектор нормали (перпендикуляр к поверхности) [-]

Магнитный поток можно наглядно представить как величину, пропорциональную числу магнитных линий, проходящих через данную площадь.

В зависимости от угла α магнитный поток может быть положительным (α 90°). Если α = 90°, то магнитный поток равен 0. Это зависит от величины косинуса угла.

Изменить магнитный поток можно меняя площадь контура, модуль индукции поля или расположение контура в магнитном поле (поворачивая его).

В случае неоднородного магнитного поля и неплоского контура, магнитный поток находят как сумму магнитных потоков, пронизывающих площадь каждого из участков, на которые можно разбить данную поверхность.

Электромагнитная индукция

Электромагнитная индукция — явление возникновения тока в замкнутом проводящем контуре при изменении магнитного потока, пронизывающего его.

Явление электромагнитной индукции было открыто М. Фарадеем.

Майкл Фарадей провел ряд опытов, которые помогли открыть явление электромагнитной индукции.

Опыт раз. На одну непроводящую основу намотали две катушки: витки первой катушки были расположены между витками второй. Витки одной катушки были замкнуты на гальванометр, а второй — подключены к источнику тока.

При замыкании ключа и протекании тока по второй катушке в первой возникал импульс тока. При размыкании ключа также наблюдался импульс тока, но ток через гальванометр тек в противоположном направлении.

Опыт два. Первую катушку подключили к источнику тока, а вторую — к гальванометру. При этом вторая катушка перемещалась относительно первой. При приближении или удалении катушки фиксировался ток.

Опыт три. Катушка замкнута на гальванометр, а магнит движется вдвигается (выдвигается) относительно катушки

Вот, что показали эти опыты:

Индукционный ток возникает только при изменении линий магнитной индукции.
Направление тока будет различно при увеличении числа линий и при их уменьшении.
Сила индукционного тока зависит от скорости изменения магнитного потока. Может изменяться само поле, или контур может перемещаться в неоднородном магнитном поле.

Почему возникает индукционный ток?

Ток в цепи может существовать, когда на свободные заряды действуют сторонние силы. Работа этих сил по перемещению единичного положительного заряда вдоль замкнутого контура равна ЭДС.

Значит, при изменении числа магнитных линий через поверхность, ограниченную контуром, в нем появляется ЭДС, которую называют ЭДС индукции.

Закон электромагнитной индукции

Закон электромагнитной индукции (закон Фарадея) звучит так:

ЭДС индукции в замкнутом контуре равна и противоположна по знаку скорости изменения магнитного потока через поверхность, ограниченную контуром.

Математически его можно описать формулой:

Закон Фарадея

Ɛi — ЭДС индукции [В]

ΔФ/Δt — скорость изменения магнитного потока [Вб/с]

Знак «–» в формуле позволяет учесть направление индукционного тока. Индукционный ток в замкнутом контуре всегда направлен так, чтобы магнитный поток поля, созданного этим током сквозь поверхность, ограниченную контуром, уменьшал бы те изменения поля, которые вызвали появление индукционного тока.

Если контур состоит из N витков (то есть он — катушка), то ЭДС индукции будет вычисляться следующим образом.

Закон Фарадея для контура из N витков

Ɛi — ЭДС индукции [В]

ΔФ/Δt — скорость изменения магнитного потока [Вб/с]

N — количество витков [-]

Сила индукционного тока в замкнутом проводящем контуре с сопротивлением R:

Закон Ома для проводящего контура

Ɛi — ЭДС индукции [В]

I — сила индукционного тока [А]

R — сопротивление контура [Ом]

Если проводник длиной l будет двигаться со скоростью v в постоянном однородном магнитном поле с индукцией B ЭДС электромагнитной индукции равна:

ЭДС индукции для движущегося проводника

Ɛi — ЭДС индукции [В]

B — магнитная индукция [Тл]

v — скорость проводника [м/с]

l — длина проводника [м]

Возникновение ЭДС индукции в движущемся в магнитном поле проводнике объясняется действием силы Лоренца на свободные заряды в движущихся проводниках. Сила Лоренца играет в этом случае роль сторонней силы.

Движущийся в магнитном поле проводник, по которому протекает индукционный ток, испытывает магнитное торможение. Полная работа силы Лоренца равна нулю.

Количество теплоты в контуре выделяется либо за счет работы внешней силы, которая поддерживает скорость проводника неизменной, либо за счет уменьшения кинетической энергии проводника.

Изменение магнитного потока, пронизывающего замкнутый контур, может происходить по двум причинам:

вследствие перемещения контура или его частей в постоянном во времени магнитном поле. Это случай, когда проводники, а вместе с ними и свободные носители заряда, движутся в магнитном поле
вследствие изменения во времени магнитного поля при неподвижном контуре. В этом случае возникновение ЭДС индукции уже нельзя объяснить действием силы Лоренца. Явление электромагнитной индукции в неподвижных проводниках, возникающее при изменении окружающего магнитного поля, также описывается формулой Фарадея

Таким образом, явления индукции в движущихся и неподвижных проводниках протекают одинаково, но физическая причина возникновения индукционного тока оказывается в этих двух случаях различной:

в случае движущихся проводников ЭДС индукции обусловлена силой Лоренца
в случае неподвижных проводников ЭДС индукции является следствием действия на свободные заряды вихревого электрического поля, возникающего при изменении магнитного поля.

Правило Ленца

Чтобы определить направление индукционного тока, нужно воспользоваться правилом Ленца.

Академически это правило звучит следующим образом: индукционный ток, возбуждаемый в замкнутом контуре при изменении магнитного потока, всегда направлен так, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызывающего индукционный ток.

Давайте попробуем чуть проще: катушка в данном случае — это недовольная бабуля. Забирают у нее магнитный поток — она недовольна и создает магнитное поле, которое этот магнитный поток хочет обратно отобрать.

Дают ей магнитный поток, забирай, мол, пользуйся, а она такая — «Да зачем сдался мне ваш магнитный поток!» и создает магнитное поле, которое этот магнитный поток выгоняет.

Источник