Есть ли мнемоническая фраза для запоминания числа e?
Для запоминания числа ПИ такая фраза есть: Это я знаю и помню прекрасно, но многие знаки мне лишни, напрасны.
А для числа e есть подобная фраза?
Может быть: Ах, мамочки! Я логарифм не полюбила, я интеграл не понимала.. . Ужас какой, вычислить невозможно! Ужас какой!
Мнемоническое правило:
два и семь, далее два раза год рождения Льва Толстого (1828), затем углы равнобедренного прямоугольного треугольника (45, 90 и 45 градусов) . Стихотворная мнемофраза, иллюстрирующая часть этого правила: «Экспоненту помнить способ есть простой: два и семь десятых, дважды Лев Толстой»
Мнемоническое стихотворение, позволяющее запомнить первые 12 знаков после запятой (длины слов кодируют цифры числа e):
Мы порхали и блистали,
Но застряли в перевале:
Не признали наши крали
Авторалли.
Это из Википедии.
А от себя, в принципе, после «2,7»:
Я, наверное, не Черчилль.
Я, наверное, не Черчилль.
Умру после 90, умру, может, на ста годах.
Так, мечтаю.. .
P.S. не в рифму, зато правда
2. Число «е». Один студент отлично знал значение числа «е» (основание натуральных логарифмов) . На вопрос: «Как он его запомнил? » — последовал ответ: «Это очень просто. Напишите 2,7 и два раза Лев Толстой» (то есть год рождения Льва Николаевича — 1828).
Вот здесь вместо 90 получается 910: «вычислить невозможно»
А в остальном — очень красиво )))
Я запомнил цифры просто на слух, они повторяются и звучат
довольно ритмично.
Источник
Экспоненту помнить способ есть простой
Формула длины окружности
З нает каждый пионер:
Длина окружности – 2 π r
Формула площади круга
Запомнит тот, кто мыслит туго:
π r (квадрат) – есть площадь круга.
Неравенство сторон треугольника
Знает даже каждый школьник
Что такое треугольник.
Но совсем не каждый знает
Сторона его любая
Даже самая большая
Меньше суммы двух сторон
Соотношения между сторонами и углами прямоугольного треугольника
У синуса буква «и» меняется на букву «о», косинуса, буква «о» меняется на букву «и».
- Биссектриса — это крыса, которая бегает по углам и делит угол пополам.
- Медиана – обезьяна, она идет по сторонам и делит стороны пополам.
Международный день числа «Пи».
Запоминание числа «Пи»
(количество букв в каждом слове соответствует значению числа «Пи» — 3,1416).
- «Это я знаю и помню прекрасно –
«Пи» многие знаки мне лишни, напрасны» »
- «Нужно только постараться
И запомнить все, как есть:
Три, четырнадцать, пятнадцать,
Девяносто два и шесть» - Три, четырнадцать, пятнадцать,
Девять, два, шесть, пять, три, пять.
Чтоб наукой заниматься,
Это каждый должен знать
Число Эйлера или Непера, не столь знаменитое как число пи , но также очень важное в математике. Число обозначается латинской буквой e и приблизительно равно 2,7182818284590452353602874713527….
- Мы порхали и блистали, но застряли в перевале; не признали наши крали авторалли.
- Два и семь, восемнадцать,
Двадцать восемь, восемнадцать,
Двадцать восемь, сорок пять,
Девяносто, сорок пять.
- Два и семь, далее два раза год рождения Льва Толстого (1828), затем углы равнобедренного прямоугольного треугольника (45, 90 и 45 градусов)
- Экспоненту помнить способ есть простой: две и семь десятых, дважды Лев Толстой
Таблица умножения для числа девять
- Положите руки на стол
- Отсчитайте слева число пальцев, равное числу, на которое нужно умножить число 9.
- Слева от этого пальца будет число десятков, справа – единиц. Сам палец, который получился в результате отсчета – не считаем.
Умножение двузначного числа на 11
Чтобы двузначное число умножить на 11 , сложите его первую и последнюю цифру. Если результат будет однозначным, впишите его между двумя цифрами первоначального числа, а если двузначным – прибавьте первую цифру результата к первой цифре первоначального числа, а вторую – впишите между цифрами.
Умножение и деление положительных и отрицательных чисел
- Закрываем любые два знака, тогда оставшийся знак- результат.
- Под плюсом понимаем друга , а под минусом — врага
Друг (+) моего врага (-) = мой враг (-)
Враг (-) моего друга (+) = мой враг (-)
Враг (-) моего врага (-) = мой друг (+)
Друг (+) моего друга (+) = мой друг (+)
Сложение и вычитание чисел с разными знаками
- черные шашки – это отрицательные числа, красные шашки – положительные. Правила игры: шашка одного цвета «съедает» шашку другого цвета. Выигрывает тот, шашек какого цвета осталось больше.
- Когда начинаем изучать неравенства, то у учащихся появляется сложность заштриховать необходимую часть луча. Чтобы ребятам было понятнее, какую часть луча штриховать , дорисовываем знак неравенства до стрелки. Стрелка указывает направление штриховки .
«Четверть. Знак. Название»
Смотрим на единичную окружность
- на π/2 и 3π/2 (расположены на оси ординат)
задаем вопрос: «будем менять название функции?» – киваем головой сверху вниз (ответ: «да»)
Источник
Экспоненту помнить способ есть простой
Эти правила помогают легче запомнить возможно большее число каких-то сведений и фактов.
Например, фраза для запоминания расположения цветов в радуге (красный, оранжевый, жёлтый, зелёный, голубой, синий, фиолетовый):
«Каждый Охотник Желает Знать, Где Сидит Фазан».
Или число «пи»=3,14158256335.
«Кто и шутя, и споро пожелает
«Пи» число узнать —
Его ужЪ знает. «
(считаем число букв)
Или фраза для запоминания расположения планет в Солнечной системе (Меркурий, Венера, Земля, Марс, Юпитер, Уран, Нептун, Плутон):
«Можно вылететь за Марс, ювелирно свернув у нашей планеты».
Или спектральная классификация звёзд в порядке уменьшения температуры, от самых горячих до самых холодных (O B A F G K M):
«Oh, Be A Fine Girl, Kiss Me» («о, будь хорошей девочкой — поцелуй меня»).
Ну, или даже принцип перевода часов на летнее или зимнее время:
Весной — Вперёд, Осенью — Обратно.
Кто ещё какие правила помнит?
А, ещё вот из русского языка:
Порядок падежей (именительный, родительный, дательный, винительный, творительный, предложный):
«Иван родил девчонку, велел тащить пелёнку».
Без мягкого знака на конце пишутся:
«Уж замуж невтерпёж».
Натти-н,
Пи=3.1415926535.
Правильно:
Кто и шутя и споро пожелаетЪ пи узнать,
число ужЪ знает.
Правило интегрирования по частям:
«Удавился утром в бане — вот дурак»
#3. «Пи=3.1415926535. «
Не вижу препятствий. Мне главное было — принцип показать.
Ой, за интегрирование по частям — отдельное спасибо; сама его всё время забываю. На всякий случай надо напомнить, что в ф-ле это выглядит так:
интеграл от (u dv) = uv — интеграл от (v du)
Если честно, я вообще-то думала, что Вы первым делом про периоды палеозоя напишете. 🙂
Ладно, напишу.
Каждый Отличный Студент Должен Курить Папиросы
Ты Юра Мал
Принеси Нам Курево
Для тех, кто не в курсе дела
Cm, O, S, D, C, P (палеозой)
T, J, K (мезозой)
Pg, N, Q (кайнозой)
P.S. Для кембрия и палеогена использованы устаревшие обозначения, новые — антикомпьютерные.
А мне во время учёбы в школе и универе помогало такое правило различения электродов:
анод (4 буквы) => ПЛЮС (тоже 4 буквы)
катод (5 букв) => МИНУС (тоже 5 букв).
Иначе запомнить невозможно.
А когда рисовали эл.схемы с источниками питания:
М_аленькая палочка — М_инус!
отечественная вики:
1. Приблизительное значение зашифровано в: «Мы порхали и блистали, но застряли в перевале; не признали наши крали авторалли» (нужно выписать подряд цифры, выражающие число букв в словах следующего стишка, и поставить запятую после первого знака)
2. Запомнить как 2, 71, и повторяющиеся 82, 81, 82
3. Мнемоническое правило: два и семь, далее два раза год рождения Льва Толстого (1828), затем углы равнобедренного прямоугольного треугольника (45, 90 и 45 градусов). Стихотворная мнемофраза, иллюстрирующая часть этого правила: «Экспоненту помнить способ есть простой: две и семь десятых, дважды Лев Толстой». Цифры 45, 90 и 45 можно запоминать как «год победы над фашистской Германией, затем дважды этот год и снова он»
4. Правила e связывается с президентом США Эндрю Джексоном: 2 — столько раз избирался, 7 — он был седьмым президентом США, 1828 — год его избрания, повторяется дважды, поскольку Джексон дважды избирался. Затем — опять-таки равнобедренный прямоугольный треугольник.
5. С точностью до трёх знаков после запятой через «число дьявола»: нужно разделить 666 на число, составленное из цифр 6 − 4, 6 − 2, 6 − 1 (три шестёрки, из которых в обратном порядке удаляются три первые степени двойки): 666 / 245
Запоминание e как 666 / (10*666^0.5 — 13)
Грубое (с точностью до 0,001), но красивое приближение полагает e равным pi * cos(pi/6). Совсем грубое (с точностью 0,01) приближение даётся выражением 5pi — 13
«Правило Боинга»: 4 sin 0.747 даёт неплохую точность 0,0005.
Стишки:
Два и семь, восемнадцать,
Двадцать восемь, восемнадцать,
Двадцать восемь, сорок пять,
Девяносто, сорок пять.
ы: самое полезное знания: корень из 3х и из 2х.
ыы: незнание всевозможных астрономических величин часто удручает 🙁
Источник
Число Эйлера, или разорится ли банк?
Недавно на просторах википедии встретила мнемоническое стихотворение, позволяющее запомнить чему равно число е: «Экспоненту помнить способ есть простой: два и семь десятых, дважды Лев Толстой». Мне оно так понравилось, что я решила написать об этом числе статью. Сегодня расскажу откуда взялось число Эйлера. И имеет ли Эйлер к нему какое-то отношение.
Для начала только уточню при чём тут Лев Толстой. Дело в том, что он родился в 1828 году. А число е ≈ 2.718281828, вот и выходит дважды Лев Толстой. Для меня это крутая мнемоника, потому что теперь я знаю и чему равно число е и год рождения Льва Николаевича :).
Ну а теперь к самому числу. Предположим у вас есть лишний 1 ₽. И вы как разумный инвестор решаете вложить его в банк. Один из банков делает вам заманчивое предложение — 100% годовых, которые начисляются в конце года. То есть в результате вы получите 2 ₽. Пытаясь вас переманить, другой банк обещает те же самые проценты, но начисления будут производиться два раза в год. Это значит, что за первые полгода сумма вашего влада увеличится до 1 ₽· (1+0.5) = 1.5 ₽, а за год 1 ₽·(1+0.5) 2 = 2.25 ₽. «Круто», — думаете вы — «может есть такой банк, который выплачивает те же самые 100%, но каждый месяц? Тогда я получу 1 ₽· (1+1/12) 12 = 2.6₽ в конце года.»
В результате вы находите банк, который предлагает увеличивать частоту начисления процентов до тех пор, пока клиент их не остановит. Ну и в чём же тут подвох?
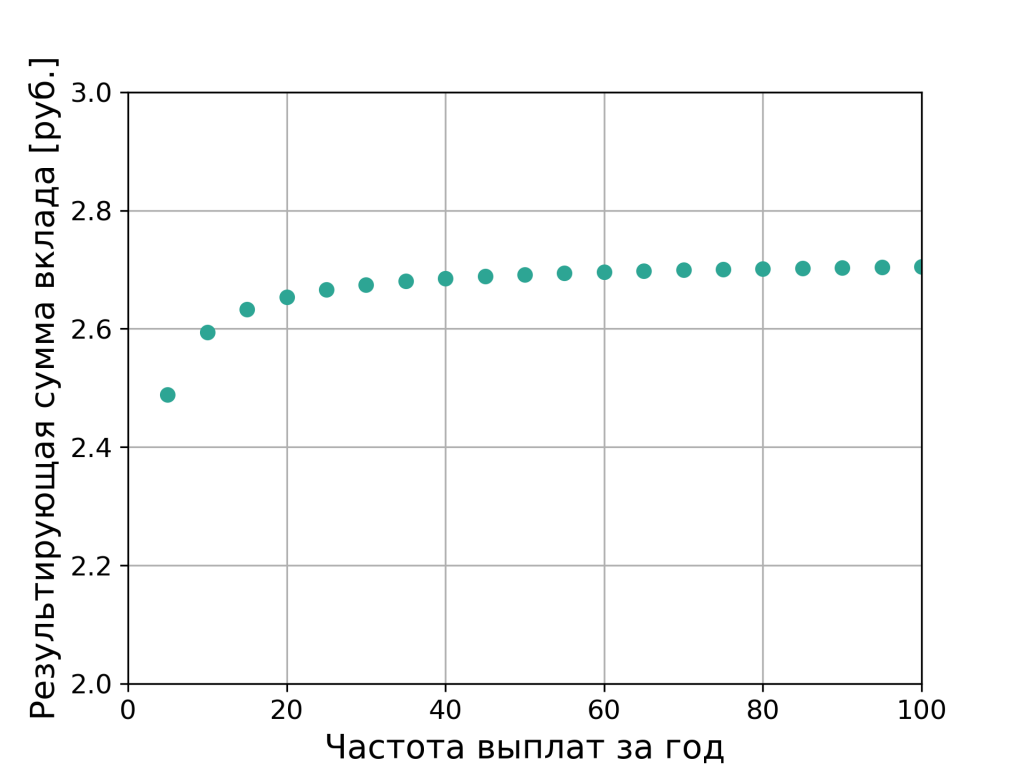
Итак, по сути мы не знаем сколько раз в год банк будет выплачивать проценты. Обозначим это количество за n. Тогда за год вклад увеличится до S = 1 ₽ · (1+1/n) n рублей. Так вот ещё в далёком 17 веке математик Якоб Бернулли вычислил, что предел такого процентного дохода равен 2.71828. Посмотрите на график:
То есть максимальная сумма, которую вам выплатит банк при 100% годовых и максимальной частоте начисления процентов, не превысит 2.72₽.
Ну понятное дело, что 100% годовых ни в одном банке вы не получите. Все дают 8% — 9% годовых. Но например, чтобы выделится среди конкурентов, маркетологи вполне могут использовать слоган: «Бесконечная частота начисления процентов при 8% годовых». Ведь они точно знают, что от этого банк не разорится.
Да, как это связано с Эйлером? Эйлер начал первым обозначать константу 2.71828 буквой e. В результате, в современном мире её называют числом Эйлера :).
Чтобы не пропустить новые статьи, подпишись на мой телеграм-канал.
Источник