Способы обработки данных физического эксперимента
GNUplot
Наверное, это самое простое, что нам могли показать в первую очередь (за исключением, пожалуй, Word или Excel). Обработка данных с помощью гнуплота предельно проста и не требует особых знаний в программировании, язык близок к алгоритмическому. Идеально подходит для начала работы над графической обработкой данных.
Как пользоваться
Пусть у нас есть файл с данными — один столбец со значениями измерений какого-то параметра. Назовем этот файл data.dat. Мы знаем, что данные представляют собой нормальное распределение, пускай это будет распределение масс партии шурупов. Наша задача заключается в определении среднего значения массы шурупа. Мое решение заключается в построении гистограммы по данным и дальнейшей ее аппроксимации кривой . Ниже привожу пример кода такого построения:
При аппроксимации будут определены значения a, b и c с достаточно хорошей точностью. В нашей задаче нетрудно догадаться, что параметр c и есть среднее значение массы измеряемых объектов. Таким образом, с помощью простого кода и некоторых соображений можно быстро проанализировать собранные данные.
Мои выводы о работе с GNUplot
В случаях, когда нужна быстрая графическая обработка большого количества данных (большого в рамках лабораторной работы), GNUplot подходит идеально. Тем не менее, иногда появляются баги, о природе которых приходится подумать. Рекомендую использовать новичкам для каких-то базовых работ, например, статистических исследований.
LabVIEW
Этот монстр предназначен для настоящих лабников! Чисто визуальная платформа для моделирования лабораторной работы. Сама собирает данные с ComPortов, сама их обрабатывает, сама строит динамические графики. Возможностей — уйма. Большинство инженеров работают именно на Labview. НО! Требует больших усилий, чтобы разобраться.
Мои выводы о работе с LabVIEW
Точно не для новичков! Если есть желание, можно посидеть пару дней и разобраться, после этого значительно сократится время обработки лабораторных работ, в которых вы можете использовать микроконтроллеры с датчиками (в моем случае это были лабораторные со всевозможными маятниками).
Python
Этот язык является отличной находкой для физиков. Чаще всего я использую его для решений задач вычислительной физики, к примеру, численное решение дифференциальных уравнений. Так же, как и гнуплот, этот язык хорош для графической обработки данных, обладает меньшим количеством багов и простотой синтаксиса (хотя и на гнуплот не жалуюсь). Лично мне больше нравится Python, но каждому — свое.
В качестве примера работы с Python привожу интерполяцию по точкам многочленом Лагранжа, потому что под рукой не оказалось более наглядного примера анализа данных . Интерполяция обычно применяется для получения приближенной формулы зависимости двух величин.
Мои выводы о работе с Python
Для меня Python является приоритетным. Гораздо больше возможностей, чем в GNUplot, не требует больших усилий, чтобы разобраться. Безусловно, использование Labview значительно профессиональнее, но так как мне лень его освоение требует внушительного количества времени, я предпочитаю осваивать все прелести Python.
Вместо заключения
В этом небольшом обзоре я решила поделиться своим опытом использования некоторых программ для обработки данных. Надеюсь, он поможет вам в вашей исследовательской деятельности.
Источник
2. Методы обработки экспериментальных данных
Эксперимент – основной общенаучный эмпирический метод исследования, научно поставленный опыт с точно учитываемыми условиями. Эксперимент обобщает ряд сопряженных понятий: опыт, целенаправленное наблюдение, воспроизведение объекта познания, организация особых условий осуществления, проверка предсказаний. Основная цель эксперимента: выявление свойств исследуемых объектов, проверка справедливости гипотез. Различают эксперименты по отраслям науки (физический, химический, социальный и т.п.), по способу формирования условий (естественный, искусственный), по целям исследования (преобразующий, констатирующий, контролирующий, поисковый, решающий), по месту проведения (лабораторный, натурный, полевой, производственный), по структуре (простой, сложный), по характеру внешних воздействий (вещественный,
энергетический, информационный), по типу моделей (материальный, мысленный), по числу варьируемых факторов (одно- и многофакторный). Методика эксперимента – это совокупность мыслительных и физических операций, размещенных в определенной последовательности, в соответствии с которой достигается цель исследований. Необходимо также обосновать набор средств измерений (приборов), машин, аппаратов. Методы измерений должны базироваться на законах метрологии, изучающей средства и методы измерений.
Получив результаты эксперимента, исследователь должен извлечь из них полезную информацию или, другими словами, провести обработку и анализ экспериментальных данных. Мы рассмотрим несколько широко используемых методов обработки и анализа экспериментальных данных, а именно: графическое представление, аппроксимацию и статистическую обработку.
2.1. Графическое представление экспериментальных данных
Графическое представление экспериментальных данных является наиболее наглядным (например, по сравнению с табличным или аналитическим), позволяет выявить общий характер функциональной зависимости изучаемых физических величин, сравнительно легко установить наличие экстремумов функции, пределов увеличения (уменьшения) функций.
Обычно при графическом представлении применяют прямоугольную систему координат. На плоскости наносят точки, отображающие экспериментальные данные (рис. 2.1). Если попытаться провести линию через все точки (в предельном случае – соединить точки отрезками прямых), то она будет иметь резкие искривления (в предельном случае – это будет ломаная линия). В естественных процессах такие искривления (на математическом языке – быстрые изменения первой производной) встречаются редко. Поскольку в экспериментальных данных всегда присутствуют ошибки измерения, график, проведенный через все экспериментальные точки, фактически отражает воздействие случайных мешающих факторов на результат измерения, а не исследуемое физическое явление. Поэтому при построении графика стараются провести плавную линию, как можно ближе проходящую ко всем экспериментальным точкам (см. раздел 2.2).
Иногда при построении графика выясняется, что некоторые точки резко удалены от кривой. В этих случаях, если нет оснований предполагать наличие скачка функции, резкое отклонение, скорее всего, объясняется грубой ошибкой измерения или промахом. Эксперимент следует повторить в диапазоне резкого отклонения данных.
Графики функций, имеющие сложный немонотонный вид (например, имеющие экстремумы), требуют тщательного вычерчивания в зонах изгибов и перегибов. На этих участках шаг изменения независимой переменой в эксперименте должен быть значительно меньше, чем на плавных участках.
Часто при проведении экспериментальных измерений приходится иметь дело с функцией двух переменных z=f (x,y). В этом случае одну из переменных, например y , при построении используют в качестве параметра. В результате график (рис. 2.2) представляет собой семейство кривых z=f(x) при y=y 1 , y=y 2 ,
Еще одна проблема при построении графика – рациональный выбор масштаба. Для увеличения точности построения необходимо, чтобы график заполнял всю площадь листа. Поэтому следует определить диапазон изменений переменных по координатным осям и соответствующим образом выбрать шкалы осей (не обязательно вести отсчет от нуля!). Масштаб осей, таким образом, получится автоматически.
Приведенные рекомендации могут оказаться недостаточными, если одна или обе переменные имеют большой диапазон изменений, например, несколько порядков. В этом случае применяют полулогарифмический y = f (lgx) или логарифмический
lg y = f (lgx) масштабы. Например, при построении частотной характеристики радиотехнического устройства широко применяется следующая разновидность логарифмического масштаба: по оси абсцисс откладывается частота в декадах lg ω , а по оси ординат – амплитуда в децибелах 20 lgA .
2.2. Аппроксимация экспериментальных данных 2.2.1 Задача аппроксимации
Термин аппроксимация (от латинского approximo ) означает замену одних математических объектов другими, более простыми и в том или ином смысле близкими к исходным.
Задача аппроксимации может возникнуть, например, при обработке экспериментальных данных, когда в результате некоторых измерений получена связь независимой переменной x и зависимой переменной y в виде таблицы значений (табл. 2.1).
Простейший пример такого эксперимента – измерение напряжения на выходе электрической цепи при различных значениях какого-либо параметра цепи или параметров входного воздействия. В результате процедуры аппроксимации должна быть получена аналитическая связь – функция y=f(x) ,
которая в дальнейшем может быть использована в расчетах как характеристика электрической цепи в целом.
Задача аппроксимации возникает также и в случае, когда для относительно сложной функции требуется получить более простое выражение, которое легко интегрируется или анализируется тем или иным стандартным методом. Например, разложение функции в ряд Тейлора (2.1) и использование в качестве аппроксимирующей функции только нескольких первых членов этого ряда (2.2) позволяет существенно упростить исходную функцию для дальнейшего анализа (2.3):
( 1 + x ) n ≈ 1 + nx ; ln ( 1 + x ) ≈ x ; sin x ≈ x ; cos x ≈ 1 при x 1 .
Очевидно, что качество аппроксимации может быть оценено двумя показателями: точность аппроксимации и простота аппроксимирующей функции, причем эти показатели противоречивы.
Процедура аппроксимации включает два этапа:
выбор типа аппроксимирующей функции (это может быть многочлен степени n , в частности, при n= 1 и n= 2 это соответственно прямая и парабола, экспонента, синусоида, гипербола, логарифмическая функция и другие функции); выбор параметров аппроксимирующей функции (коэффициентов
многочлена, показателя экспоненты, амплитуды, частоты и фазы синусоиды и т.д.), обеспечивающих наилучшее приближение аппроксимирующей функции к исходным данным. При этом обязательно должен быть заранее сформулирован критерий оценки качества приближения.
Если исходная экспериментальная или расчетная зависимость задана в виде набора точек ( x i , y i ), i= 1,2,…, k , где k — количество точек, то при аппроксимации возникает естественное желание наиболее полно использовать имеющуюся информацию: то есть подобрать такую функцию, значения которой во всех точках x i совпадают со значениями y i . Эта задача была решена во второй половине XVIII века французским математиком
Лагранжем, который предложил так называемый «интерполяционный
многочлен n -го порядка» в виде суммы ( n+ 1) слагаемых:
( x − x 2 )( x − x 3 ) . ( x − x n + 1 )
( x − x 1 )( x − x 3 ) . ( x − x n + 1 )
( x − x 1 )( x − x 2 ) . ( x − x n )
Интерполяционный многочлен (2.4) – частный случай аппроксимирующей функции – позволяет вычислить значение f(x)=P n (x) для любого x ( interpole – между точками), причем в узлах интерполяции – точках ( x i , y i ) выполняется
P n (x i ) = y i , i = 1 ,…,n+ 1 .
Интерполяционный многочлен n -го порядка проходит через k = n + 1 исходных точек. Если точек достаточно много, то и многочлен будет иметь высокую степень, то есть аппроксимирующая функция получится сложной. Кроме того, стремление провести аппроксимирующую функцию через исходные точки, особенно при их экспериментальном происхождении, не разумно из-за наличия ошибок измерения. Поэтому следует ограничиться невысокой степенью многочлена n = 1,2,3, так, чтобы график аппроксимирующей функции, соответственно прямая, парабола или кубическая парабола, адекватно отражал общий ход экспериментальной зависимости.
При таком подходе количество определяемых параметров аппроксимирующей функции меньше количества точек k , используемых для этого. Поэтому необходимо выбрать специальные критерии качества аппроксимирующей функции. На практике чаще других используются следующие два критерия: критерий равномерного приближения и критерий наименьших квадратов .
2.2.2. Критерий равномерного приближения
Предположим, что тип аппроксимирующей функции выбран, и теперь необходимо определить ее параметры. Критерий равномерного приближения означает минимизацию наибольшего отклонения f(x) в точках x = x i от исходных значений y i
Для аппроксимирующей функции – степенного многочлена
f ( x ) = a 0 + a 1 x + a 2 x 2 + . + a n x n = ∑ a j x j ,
сформулируем оптимизационную задачу в соответствии с выбранным критерием (2.5) следующим образом
y i − ∑ a j x i j
≤ z , i = 1,2. k ; n k
где переменными являются z и a j .
Если каждое из неравенств в (2.6), содержащее знак абсолютной величины, представить в виде двух обычных неравенств, то задача сводится к варианту задачи линейного программирования и может быть решена с помощью симплекс-метода [1].
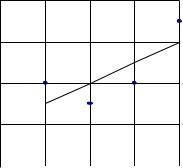
Пример 2.1. Для результатов измерений, приведенных в табл.2.2 найти равномерное приближение для аппроксимирующей функции вида f(x)= a 0 + a 1 x.
оптимизационную задачу (2.6) для k = 4, n = 1.
и представим каждое из неравенств, содержащее знак абсолютной величины, в виде двух обычных неравенств
a 0 + a 1 + z − 2 ≥ 0
− a 0 − a 1 + z + 2 ≥ 0
a 0 + 2 a 1 + z − 1,5 ≥ 0
− a 0 − 2 a 1 + z + 1,5 ≥ 0
a 0 + 3 a 1 + z − 2 ≥ 0
− a 0 − 3 a 1 + z + 2 ≥ 0
a 0 + 4 a 1 + z − 3,5 ≥ 0
− a 0 − 4 a 1 + z + 3,5 ≥ 0
Для того, чтобы качественно описать решение задачи (2.7) – задачи линейного программирования – воспользуемся пространственным представлением. В трехмерном пространстве неизвестных ( a 0 , a 1 , z ) каждое их восьми неравенств определяет полупространство, находящееся над соответствующей плоскостью. Например, для первого неравенства – такую плоскость описывает уравнение z = – a 0 – a 1 + 2 . Полупространство над этой плоскостью, с учетом условия z ≥ 0, есть область возможных значений неизвестных, удовлетворяющих первому неравенству. Построив все восемь плоскостей, получим некоторую причудливую область пространства в форме многогранника, находящуюся над всеми этими плоскостями. Самая нижняя точка этой области, ближайшая к плоскости z = 0, и будет решением задачи
К сожалению, графическое изображение описанной процедуры на плоском листе бумаги практически невозможно было бы воспринять. Рекомендуем читателю попробовать самостоятельно решить задачу в двумерном представлении по следующему алгоритму, используя неизвестное z в качестве параметра. Запишем восемь исходных неравенств в несколько ином виде
a 1 ≥ − a 0 + 2 − z (1)
a 1 ≤ − a 0 + 2 + z
При некотором значении параметра z , например z = 1, каждое из неравенств определяет полуплоскость, находящуюся над или под соответствующей прямой. Построив все восемь прямых, можно определить область плоскости ( a 0 ,a 1 ) в форме многоугольника, которая удовлетворяет всем восьми неравенствам. Эта область в нашем примере будет ограничена прямыми 1,4,6 и 7. Если далее уменьшать значение параметра z , то площадь области будет уменьшаться и при z = 0,5 окажется, что область пространства стянется в точку с координатами a 0 = 1, a 1 =0,5.
Таким образом, искомое равномерное приближение есть f(x) =1 + 0,5 x. На рис. 2.3 изображены точки, отражающие исходные данные табл. 2.2, и график аппроксимирующей функции.
2.2.3. Критерий наименьших квадратов
Критерий наименьших квадратов означает минимизацию суммы V квадратов отклонений значений аппроксимирующей функции в точках x i от экспериментальных значений y i
V = ∑ ( y i − f ( x i )) 2 → min
или, для аппроксимирующей функции – степенного многочлена,
V = ∑ ( y i − ∑ a j x i j ) 2 → min; n k ,
где переменными являются коэффициенты многочлена a j . Требуемый минимум имеет место, при равенстве нулю всех ( n+ 1) частных производных функции V , т.е. при ∂ V 
Частная производная при j=m имеет вид
= 2 ∑ y i − ∑ a j x i
и, таким образом, реализация выбранного критерия сводится к решению системы ( n+ 1) линейных (это очень важно для последующего решения) уравнений с ( n+ 1) неизвестными a j
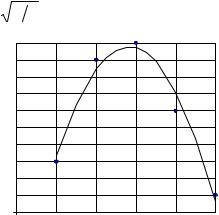
Пример 2.2. Найти аппроксимирующую функцию в виде f(x)=a 0 +a 1 x+a 2 x 2 , наилучшую по критерию наименьших квадратов, для результатов измерений, приведенных в табл.2.3.
Запишем систему (2.10)
для трех неизвестных a 0 , a 1 и a 2 .
∑ i = 5 ( y i − a 0 − a 1 x i − a 2 x i 2 ) = 0
∑ i = 5 ( y i x i − a 0 x i − a 1 x i 2 − a 2 x i 3 ) = 0
∑ i = 5 ( y i x i 2 − a 0 x i 2 − a 1 x i 3 − a 2 x i 4 ) = 0 i = 1
и преобразуем ее к стандартному виду
Подставив значения x i и y i
из табл.2.3, получим систему
225 a 1 + 979 a 2 = 250 ,
решение которой a 0 ≈ – 5,6 , a 1 ≈ 10,9, a 2 ≈ – 1,93.
Таким образом, искомое приближение по методу наименьших квадратов есть f(x) = – 5,6 + 10,9 x – 1,93 x 2 . На рис. 2.4 изображены точки, отражающие исходные данные табл. 2.3, и график аппроксимирующей функции. Средний квадрат модуля отклонения аппроксимирующей функции от экспериментальных значений (среднеквадратическая ошибка) составляет
До сих пор в качестве аппроксимирующей функции рассматривался степенной многочлен, являющийся линейным относительно своих параметров – коэффициентов a 0 , a 1 ,…, a n . Поэтому удавалось решить аналитически линейную систему уравнений относительно этих параметров. Однако, на практике, исходя из имеющихся экспериментальных данных и априорной информации о физических законах, реализующихся в эксперименте, могут быть выбраны и другие аппроксимирующие функции, в которых параметры входят нелинейно .
Например, для результатов измерений, изображенных на рис. 2.5, а и б , целесообразно выбрать соответственно
f ( x ) = c + ae bx
Подобные экспериментальные данные могут быть получены, соответственно при измерении частотной зависимости коэффициента передачи электронной схемы и при записи переходного теплового или электрического процессов.
Если непосредственно применить критерий наименьших квадратов для выбора параметров предложенных функций, то мы столкнемся с системой нелинейных уравнений, которая, возможно, не будет иметь аналитического решения. В принципе эта ситуация не является тупиковой – можно применить численные методы. Чтобы избежать этого, применяется метод линеаризации .
Суть метода состоит в переходе к новым переменным, которые входили бы в аппроксимирующую функцию линейно. Положив для функции (2.9) Y=1/y, A 0 = a, A 1 = b, X = x , получим линейную зависимость Y= F(X)= A 0 +A 1 X , эквивалентную исходной. Экспериментальные данные должны быть пересчитаны по приведенным формулам (в данном случае только значения Y i =1/y i ), и далее может быть применен критерий наименьших квадратов.
В случае (2.10) аналогичная линеаризация Y=F(X)= A 0 + A 1 X достигается, если положить Y = ln ( y-c ), A 0 = lna , A 1 = b, X = x. Чтобы пересчитать экспериментальные данные по этим формулам необходимо предварительно определить значение c. Обычно на практике значение c может быть специально измерено. В противном случае это можно сделать, исходя из рассмотрения экспериментальных данных, нанесенных в виде точек на плоскость xoy , и, в дальнейшем уточнить значение c путем его вариаций.
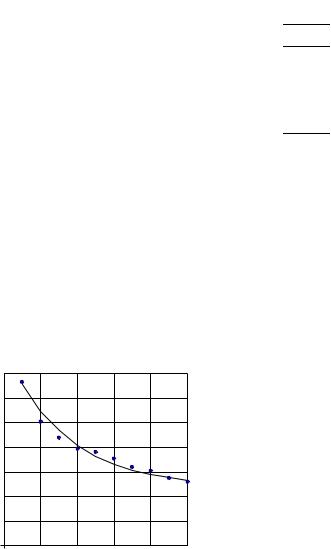
Пример 2.3. Рассмотрим пример аппроксимации с использованием метода линеаризации и критерия наименьших квадратов для экспериментальных данных, заданных следующей таблицей (первые три строки табл. 2.4):
Нанесем экспериментальные точки на плоскость xoy (рис.2.6). Ход экспериментальной зависимости определяет тип функции (2.10) –
Пересчитываем экспериментальные значения по формуле Y i = ln ( y i — c ) и записываем результаты в табл. 2.4. Теперь для пар значений (x i ,Y i ) , используя критерий наименьших квадратов, можно построить аппроксимирующую функцию в виде F(X)=A 0 + A 1 X= = 2,57 – 0,036 x. Тогда аппроксимирующая функция для исходных данных будет иметь вид f ( x ) = 15,0 + 13,0 e . Среднеквадратическая ошибка аппроксимации составит σ = 0,58 .
Этот результат может быть улучшен путем небольших вариаций параметра c .
В частности, при c =
14,8 получим аппроксимирующую функцию в
виде f ( x ) = 14,8 + 11,2 e − 0,030 x и
среднеквадратическую ошибку σ = 0,40 . График
этой функции изображен на рис.2.6. Процесс уточнения параметра c может быть продолжен.
В заключение данного раздела для читателя, уже получившего некоторый опыт решения задач аппроксимации экспериментальных данных, сделаем следующее замечание. Данную задачу можно рассматривать как частный случай огромного класса так называемых обратных задач . В отличие от прямых задач , когда по известным формулам, отражающим физические законы, вычисляются значения физических величин, при решении обратных задач, наоборот, по известным значениям физических величин необходимо
восстановить параметры, входящие в формулы физических законов, а, возможно, и выбрать сами эти формулы.
Например, если задано положение в пространстве и величина электрического заряда одного или нескольких точечных источников электрического поля, мы сможем вычислить по формулам электростатики напряженность электрического поля в любой точке пространства (прямая задача). Обратная задача в этом случае состоит в определении местоположения и величины зарядов точечных источников по известной напряженности электрического поля, измеренной в произвольном числе точек пространства. При решении такой задачи необходимо сначала выбрать модель поля – число источников, а затем определить их параметры: местоположение и заряд. Здесь очевидна аналогия с задачей аппроксимации экспериментальных данных – сначала выбор типа аппроксимирующей функции, затем – определение ее параметров.
Общая теория обратных задач разработана академиком А.Н. Тихоновым [2,3]. При решении обратных задач основными вопросами являются наличие и единственность решения, а также его устойчивость к малым вариациям исходных данных (например, искажениям результатов измерений под действием помех).
По аналогии с обратными задачами и при аппроксимации экспериментальных данных методом наименьших квадратов существует проблема устойчивости. Эта проблема может проявиться при решении системы уравнений типа (2.8). Главный определитель этой системы под действием малых случайных ошибок измерения может оказаться близким к нулю, что приведет к большой среднеквадратической ошибке аппроксимации.
В последнее время в связи с бурным развитием вычислительной техники и повышением ее быстродействия стало возможным решение обратных задач методом случайных испытаний (методом Монте-Карло [6], см. раздел 4.1.), когда решение обратной задачи заменяется многократным решением прямой задачи при вариации значений искомых параметров. За решение обратной задачи принимается наилучшая из попыток по выбранному заранее критерию.
В принципе такой метод может быть использован и при аппроксимации экспериментальных данных при выбранном критерии качества. Определив тип аппроксимирующей функции можно далее испытывать различные случайные наборы значений параметров этой функции с тем, чтобы выбрать из них наилучший.
2.3. Статистическая обработка экспериментальных
При проведении измерений в рамках научных экспериментов исследователь получает некоторый результат, который носит случайный характер. Для характеристики этого факта используется термин «неопределенность результата измерения». Уменьшение неопределенности результата измерения
возможно путем многократного повторения эксперимента и дальнейшего анализа результатов – статистической обработки.
При наличии некоторого большого массива измерений может быть поставлена задача определения закона распределения случайной величины или проверки гипотезы о том или ином законе распределения [4]. При относительно небольшом числе измерений можно поставить задачу определить, хотя бы приближенно, важнейшие числовые характеристики случайной величины. Например, если заранее известно, что случайная величина X имеет нормальное распределение, необходимо определить его параметры: математическое ожидание m x и среднеквадратическое отклонение
Значение параметра, вычисленное на основе ограниченного числа опытов, всегда будет случайным. Поэтому следует говорить не об определении, а об оценке параметра. Ошибка в оценке в среднем тем больше, чем меньше значение n .
Оценка параметра закона распределения должна отвечать следующим требованиям:
состоятельность – при увеличении числа наблюдений ( n → ∞ ) оценка параметра должна стремиться к его истинному значению; несмещенность – математическое ожидание оценки параметра должно быть равно его истинному значению (отсутствие систематической ошибки); эффективность – дисперсия оценки параметра должна быть минимальной. Различают генеральную и выборочную совокупности измерений. Генеральная совокупность – это множество результатов всех измерений, которые в принципе можно провести. Генеральная совокупность может быть конечной (например, при определении среднего роста студентов университета можно действительно измерить рост всех студентов без исключения) или бесконечной (например, при определении среднего значения шума можно сделать сколь угодно много измерений его мгновенных значений). Выборочная совокупность (выборка из генеральной совокупности) предполагает ограниченное, относительно небольшое число измерений (например, при изучении общественного мнения россиян в опросе обычно участвуют не более 0,01% населения).
Приведем формулы для оценок математического ожидания
случайной величины X , полученных по результатам
Источник