Экономический анализ интегральным способом

Интегральный способ детерминированного факторного анализа

Как известно, в детерминированном факторном анализе используют следующие основные способы:

• способ цепных подстановок;
• способ абсолютных разниц;
• способ относительных (процентных) разниц;
• интегральный метод и др.

Интегральный метод позволяет достигнуть полного разложения результативного показателя по факторам и носит универсальный характер – применяется для измерения влияния факторов в мультипликативных, кратных и смешанных моделях.

Использование этого способа позволяет получить более точные результаты по сравнению с остальными выше названными способами, поскольку дополнительный прирост результативного показателя от взаимодействия факторов присоединяется не к последнему фактору, а делится поровну между ними.

Рассмотрим алгоритмы расчетов влияния факторов для различных моделей, приводимые в специальной литературе:

Мультипликативная модель вида f = x*y:

Δf(x) = Δx*y0 + ½Δx*Δy, или Δf(x) = ½Δx (y0 + y1);
Δf(y) = Δy*x0 + ½Δx*Δy, или Δf(y) = ½Δy (x0 + x1);
где x0, y0 – базисные (плановые) значения факторов, оказывающих влияние на результативный показатель; x1, y1 — фактические значения факторов; Δx = x1-x0, Δy = y1-y0 — абсолютные изменения (отклонения) факторов х, у соответственно;

Мультипликативная модель вида f = x*y*z:

Δf(x) = ½Δx (y0*z1 + y1*z0) + ⅓Δx*Δy*Δz;
Δf(y) = ½Δy (x0*z1 + x1*z0) + ⅓Δx*Δy*Δz;
Δf(z) = ½Δz (x0*y1 + x1*y0) + ⅓Δx*Δy*Δz;

Кратная модель вида f = x/y:

Δf(x) = Δx/Δy * ln |y1/y0|;
Δf(y) = Δf — Δf(x) = (f1-f0) — Δf(x);

Смешанная модель вида f = x/(y+z):

Δf(x) = Δx/(Δy+Δz) * ln |(y1+z1)/(y0+z0)|;
Δf(y) = (Δf — Δf(x))Δy / (Δy+Δz);
Δf(z) = (Δf — Δf(x))Δz / (Δy+Δz).

Пример применения интегрального способа для факторного анализа

Порядок применения интегрального способа рассмотрим на следующем примере. Проанализировать влияние на валовый объем производства количества работников и их выработки интегральным способом. Исходные данные представлены в таблице.

Показатель	Условное обозначение	Базисное значение (0)	Фактическое значение (1)	Изменение (+,-)
				Абсолютное	Относительное, %
Объем валовой продукции, тыс. руб.	ВП	2920	3400	+480	16,40
Среднесписочная численность персонала, чел.	ЧР	20	25	+5	25,00
Среднегодовая выработка продукции одним работником, тыс. руб.	ГВ	146	136	-10	-6,85

Решение. Зависимость объема производства продукции от данных факторов можно описать с помощью двухфакторной мультипликативной модели: ВП = ЧР * ГВ.

Алгоритм расчета влияния факторов интегральным способом таков:

• ΔВП(ЧР) = ΔЧР*ГВ0+½ΔЧР*ΔГВ = 5*146+0,5*5*(-10) = 705 тыс. руб. — влияние изменения численности персонала на объем производства;
• ΔВП(ГВ) = ΔГВ*ЧР0+½ΔЧР*Δ(-10) = -10*20+0,5*5*(-10) = -225 тыс. руб. — влияние изменения среднегодовой выработки продукции одним работником на объем производства;
• ΔВП = ΔВП(ЧР)+ ΔВП(ГВ) = 705 + (-225) = 480 тыс. руб. — суммарное влияние двух факторов.

Таким образом, использование интегрального метода знания основ интегрирования. Достаточно в готовые рабочие формулы подставить числовые данные и сделать расчеты.

Источник

Интегральный способ в экономическом анализе

Основные недостатки метода элиминирования. Проблема разложения дополнительного прироста от взаимодействия факторов между ними. Сущность интегрального метода и сфера его применения. Алгоритмы расчета влияния факторов в разных моделях интегральным способом

Элиминирование как способ детерминированного факторного анализа имеет существенный недостаток. При его использовании исходят из того, что факторы изменяютсянезависимо друг от друга. На самом же деле они изменяютсясовместно, взаимосвязано и от этого взаимодействия получается дополнительный прирост результативного показателя, который при применении способов элиминирования присоединяется к одному из факторов, как правило к последнему. В связи с этим величина влияния факторов на изменение результативного показателя меняется в зависимости отместа, на которое поставлен тот или иной фактор в детерминированной модели.

Рассмотрим это на примере, который дан в табл.7.1. Согласно приведенным в ней данным, количество работников на предприятии увеличилось на 20%, производительность труда — на 25%, а объем валовой продукции — на 50%. Это значит, что 5% (50 — 20 — 25), или 8000 тыс руб. валовой продукции составляет дополнительный прирост от взаимодействия обоих факторов.

Когда мы подсчитаем условный объем валовой продукции, исходя из фактического количества работников и планового уровня производительности труда, то весь дополнительный прирост от взаимодействия двух факторов относится к качественному фактору — изменению производительности труда:

ВП= КРГВ=1000160= 160 000 руб.,

ВП= КРГВ=1200*160=192 000 руб.,

ВП= КРГВ=1200200=240 000 руб.

=ВП-ВП=192 000 — 160 000=+32 000 руб. .

=ВП-ВП=240 000— 192 000=+48 000 руб. .

Если же при расчете условного объема валовой продукции взять запланированное количество работников и фактический уровень производительности труда, то весь дополнительный прирост валовой продукции относится к количественному фактору, который мы изменяем во вторую очередь:

ВП= КРГВ=1000160= 160 000 руб.

ВП= КРГВ=1000*200=200 000 руб.,

ВП= КРГВ=1200200=240 000 руб.

=ВП-ВП=240 000— 200 000=+40 000 руб.

=ВП-ВП=200 000 — 160 000=+40 000 руб. .

Покажем графическое решение задачи в разных вариантах (рис. 7.2).

В первом варианте расчета условный показатель имеет форму: ВП=КРГВ; во втором —- ВП= КРГВ

B C B C

КР

КРА Д А Д

ГВГВГВГВ

Рис 7.2. Графическое решение задачи деления дополнительного прироста при использовании способов элиминирования.

Соответственно отклонения за счет каждого фактора в первом случае

; ;

; ;

На графиках этим отклонениям соответствуют разные прямоугольники, так как при разных вариантах подстановки величина дополнительного прироста результативного показателя, равная прямоугольнику АВСD, относится в первом случае к величине влиянии годовой выработки, а во втором — к величине влияния количества работников. В результате этого величина влияния одного фактора преувеличивается, а другого — приуменьшается, что вызывает неодно значность оценки влияния факторов, особенно в тех случаях, когда дополнительный прирост довольно существенный, как в нашем примере.

Чтобы избавиться от этого недостатка, в детерминированном факторном анализе используется интегральный метод, который применяется для измерения влияния факторов в мультипликативных, кратных и смешанных моделях типа У=А/Xi. Последняя представляет собой сочетание кратной и аддитивной моделей. Использование этого способа позволяет получать более точные результаты расчета влияния факторов по сравнению со способами цепной подстановки, абсолютных и относительных разниц и избежать неоднозначной оценки влияния факторов потому, что в данном случае результатыне зависят от местоположения факторов в модели, а дополнительный прирост результативного показателя, который образовался от взаимодействия факторов, раскладывается между ними поровну.

На первый взгляд может показаться, что для распределения дополнительного прироста достаточно взять его половину или часть, соответствующую количеству факторов. Но это сделать чаще всего сложно, так как факторы могут действовать в разных направлениях. Поэтому в интегральном методе пользуются определенными формулами.

Для двухфакторной мультипликативной модели F=XY:

; .

В нашем примере (см.табл.7.1) расчет проводится следующим образом:

=200160+1/220040=36 000 руб.;

=401000+1/220040=44 000 руб.

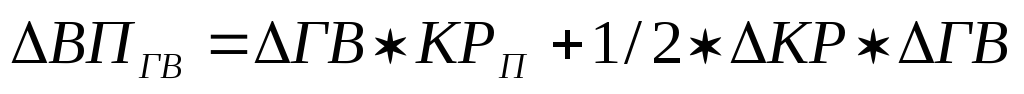
Использование интегрального метода не требует знания всего процесса интегрирования. Достаточно в готовые рабочие формулы подставить необходимые числовые данные и сделать несложные расчеты.

Источник