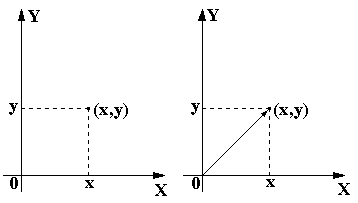- Двумерная дискретная случайная величина
- Система двух случайных величин: теория
- Примеры решений
- Решебник по теории вероятности онлайн
- Двумерная непрерывная случайная величина
- Система непрерывных случайных величин: теория
- Примеры решений
- Решебник по теории вероятности онлайн
- 5.2. Векторные случайные величины
- 5.2.1. Функция распределения двумерного случайного вектора
- Двумерный случайный вектор
- Основные числовые характеристики дискретной случайной величины. Свойства математического ожидания. Исследование двумерного дискретного случайного вектора. Частные распределения по компонентам и их характеристики. Ковариационная и корреляционная матрицы.
- Отправить свою хорошую работу в базу знаний просто. Используйте форму, расположенную ниже
- Подобные документы
Двумерная дискретная случайная величина
Ранее мы разобрали примеры решений задач для одномерной дискретной случайной величины. Но бывает, что результат испытания описывается не одной, а несколькими случайными величинами (случайным вектором).
В случае двух величин (скажем, $X$ и $Y$) мы имеем дело с так называемой двумерной дискретной случайной величиной $(X,Y)$ (или системой случайных одномерных величин). Кратко выпишем основы теории.
Система двух случайных величин: теория
Двумерная ДСВ задается законом распределения (обычно представленным в виде таблицы распределения):
$$ P(X=x_i, Y=y_k)=p_
По нему можно найти одномерные законы распределения (составляющих):
$$ p_i=P(X=x_i)=\sum_
Интегральная функция распределения задается формулой $F(x,y)=P(X\lt x, Y\lt y)$. Даже для самого простого закона распределения 2 на 2 функция занимает 5 строк, поэтому ее редко выписывают в явном виде.
Если для любой пары возможных значений $(X=x_i, Y=y_k)$ выполняется равенство
$$P(X=x_i, Y=y_k)=P(X=x_i)\cdot P(Y=y_k),$$
то случайные величины $X, Y$ называются независимыми.
Если случайные величины зависимы, для них можно выписать условные законы распределения (для независимых они совпадают с безусловными законами):
Для случайных величин $X,Y$, входящих в состав случайного вектора, можно вычислить ковариацию и коэффициент корреляции по формулам:
Далее вы найдете разные примеры задач с полным решением, где используются дискретные двумерные случайные величины (системы случайных величин).
Примеры решений
Задача 1. В продукции завода брак вследствие дефекта А составляет 10%, а вследствие дефекта В — 20%. Годная продукция составляет 75%. Пусть X — индикатор дефекта А, a Y — индикатор дефекта В. Составить матрицу распределения двумерной случайной величины (X, Y). Найти одномерные ряды распределений составляющих X и У и исследовать их зависимость.
Задача 2. Два баскетболиста по два раза бросают мяч в корзину. При каждом броске вероятность попадания для первого баскетболиста 0,6, для второго – 0,7. Случайная величина X – число попаданий первым баскетболистом по кольцу. Случайная величина Y – суммарное число попаданий обоими баскетболистами. Построить таблицу распределения случайного вектора (X,Y). Найти характеристики вектора (X,Y). Зависимы или независимы случайные величины X и Y.
Задача 3. Слово РОССИЯ разрезано по буквам. Случайным образом вынимаем две буквы, тогда X – количество гласных среди них, затем вынимаем еще две буквы и Y – количество гласных во второй паре. Составить закон распределения системы случайных величин X, Y.
Задача 4. $X, Y$ — индикаторы событий $A, B$, означающий положительные ответы соответственно на вопросы $\alpha, \beta$ социологической анкеты. По данным социологического опроса двумерная случайная величина $(X,Y)$ имеет следующую таблицу распределения.
Положительному ответу присвоен ранг 1, отрицательному – 0.
Найти коэффициент корреляции $\rho_
Задача 5. Составить закон распределения X — сумм очков и Y — числа тузов при выборе двух карт из колоды, содержащей только тузов, королей и дам (туз=11, дама=3, король=4)
Найти законы распределения величин Х и Y. Зависимы ли эти величины? Написать функцию распределения для (Х, Y). Построить ковариационный граф. Посчитать ковариацию (X,Y). Написать ковариационную матрицу. Посчитать корреляцию (X,Y) и написать корреляционную матрицу.
Задача 6. Бросаются две одинаковые игральные кости. Случайная величина X равна 1, если сумма выпавших чисел четна, и равна 0 в противном случае. Случайная величина Y равна 1, если произведение выпавших чисел четно, и 0 в противном случае. Описать закон распределения случайного вектора (X,Y). Найти D[X], D[Y] и cov[X,Y].
Задача 7. В урне лежат 100 шаров, из них 25 белых. Из урны последовательно вынимают два шара. Пусть $X_i$ – число белых шаров, появившихся при $i$-м вынимании. Найти коэффициент корреляции между величинами $X_1$ и $X_2$.
Задача 8. Для заданного закона распределения вероятностей двухмерной случайной величины (Х, Y):
Y\X 2 5
8 0,15 0,10
10 0,22 0,23
12 0,10 0,20
Найти коэффициент корреляции между величинами Х и Y.
Задача 9. Задана дискретная двумерная случайная величина (X,Y).
А) найти безусловные законы распределения составляющих;
Б) построить регрессию случайной величины Y на X;
В) построить регрессию случайной величины X на Y;
Г) найти коэффициент ковариации;
Д) найти коэффициент корреляции.
20 30 40 50 70
3 0,01 0,01 0,02 0,02 0,01
4 0,04 0,3 0,06 0,03 0,01
5 0,02 0,03 0,06 0,07 0,05
9 0,05 0,03 0,04 0,02 0,03
10 0,03 0,02 0,01 0,01 0,02
Задача 10. Система (x, y) задана следующей двумерной таблицей распределения вероятностей. Определить:
А) безусловные законы распределения составляющих;
Б) условный закон распределения y при x=1;
В) условное математическое ожидание x при y=2.
Г) вероятность того, что случайная величина (x,y) будет принадлежать области $|x|+|y|\le 3$.
-3 0 2
-1 0 0,1 0,15
1 0,05 0,3 0,05
2 0,15 0,05 0,15
Решебник по теории вероятности онлайн
Больше 11000 решенных и оформленных задач по теории вероятности:
Источник
Двумерная непрерывная случайная величина
Ранее мы разобрали примеры решений задач для одномерной непрерывной случайной величины. Перейдем к более сложному случаю — двумерной непрерывной случайной величине $(X,Y)$ (или двумерному вектору). Кратко выпишем основы теории.
Система непрерывных случайных величин: теория
Двумерная непрерывная СВ задается своей функцией распределения $F(x,y)=P(X\lt x, Y\lt y)$, свойства которой аналогичны свойствам одномерной ФР. Эта функция должна быть непрерывна, дифференцируема и иметь вторую смешанную производную, которая будет как раз плотностью распределения вероятностей системы непрерывных случайных величин:
Зная плотность совместного распределения, можно найти одномерные плотности для $X$ и $Y$:
Вероятность попадания случайного вектора в прямоугольную область можно вычислить как двойной интеграл от плотности (по этой области) или через функцию распределения:
$$P(x_1 \le X \le x_2, y_1 \le Y \le y_2) = F(x_2, y_2)-F(x_1, y_2)-F(x_2, y_1)+F(x_1, y_1).$$
Как и для случая дискретных двумерных СВ вводится понятие условного закона распределения, плотности которых можно найти так:
Если для всех значений $(x,y)$ выполняется равенство
то случайные величины $X, Y$ называются независимыми (их условные плотности распределения совпадают с безусловными). Для независимых случайных величин выполняется аналогичное равенство для функций распределений:
Для случайных величин $X,Y$, входящих в состав случайного вектора, можно вычислить ковариацию и коэффициент корреляции по формулам:
В этом разделе мы приведем примеры задач с полным решением, где используются непрерывные двумерные случайные величины (системы случайных величин).
Примеры решений
Задача 1. Дана плотность распределения вероятностей системы $$ f(x)= \left\< \begin
$C, \rho_1(x), \rho_2(y), m_x, m_y, D_x, D_y, cov(X,Y), r_
Задача 2. Дана плотность распределения $f(x,y)$ системы $X,Y$ двух непрерывных случайных величин в треугольнике АВС.
1.1. Найдите константу с.
1.2. Найдите $f_X(x), f_Y(y)$ — плотности распределения с.в. Х и с.в. Y.
Выясните, зависимы или нет с.в. Х и Y. Сформулируйте критерий независимости системы непрерывных случайных величин.
1.3. Найдите математическое ожидание и дисперсию с.в. Х и с.в. Y. Поясните смысл найденных характеристик.
1.4. Найдите коэффициент корреляции с.в. Х и Y. Являются ли случайные величины коррелированными? Сформулируйте свойства коэффициента корреляции.
1.5. Запишите уравнение регрессии с.в. Y на Х и постройте линию регрессии в треугольнике АВС.
1.6. Запишите уравнение линейной среднеквадратичной регрессии с.в. Y на Х и постройте эту прямую в треугольнике АВС. $$ f(x,y)=c\sqrt
Задача 3. Интегральная функция распределения случайного вектора (X,Y): $$ F(x)= \left\< \begin
Задача 4. Плотность совместного распределения непрерывной двумерной случайной величины (Х, У) $$f(x,y)=C e^<-x^2-2xy-4y^2>$$ Найти:
а) постоянный множитель С;
б) плотности распределения составляющих;
в) условные плотности распределения составляющих.
Задача 5. Задана двумерная плотность вероятности системы двух случайных величин: $f(x,y)=1/2 \sin(x+y)$ в квадрате $0 \le x \le \pi/2$, $0 \le y \le \pi/2$, вне квадрата $f(x,y)=0$. Найти функцию распределения системы (X,Y).
Задача 6. Определить плотность вероятности, математические ожидания и корреляционную матрицу системы случайных величин $(X,Y)$, заданных в интервалах $0 \le x \le \pi/2$, $0 \le y \le \pi/2$, если функция распределения системы $F(x,y)=\sin x \sin y$.
Задача 7. Плотность вероятности системы случайных величин равна $$f(x,y) = c(R-\sqrt
А) постоянную $c$;
Б) вероятность попадания в круг радиуса $a\lt R$, если центры обоих кругов совпадают с началом координат.
Задача 8. Совместная плотность вероятности системы двух случайных величин X и Y $$f(x,y)=\frac
Решебник по теории вероятности онлайн
Больше 11000 решенных и оформленных задач по теории вероятности:
Источник
5.2. Векторные случайные величины
При совместном изучении нескольких случайных величин их рассматривают как систему случайных величин, либо как случайный вектор, компонентами которого являются отдельные случайные величины. Система двух случайных величин (Х, Y) геометрически интерпретируется как случайный вектор на плоскости X0Y (рис.57), направленный из начала координат в точку (Х, Y) или как случайная точка на плоскости X0Y с координатами (Х, Y). Система трех случайных величин может рассматриваться как вектор в трехмерном пространстве, система n случайных величин — как вектор в n— мерном пространстве. Далее ограничимся рассмотрением системы двух случайных величин.
Рис.57. Двумерный случайный вектор
Рис.58. Двумерная функция распределения — вероятность попадания случайной точки в заштрихованную область
5.2.1. Функция распределения двумерного случайного вектора
Функция распределения системы двух случайных величин (двумерного случайного вектора)- это вероятность совместного выполнения двух неравенств Х x1;
2. Повсюду на - функция распределения равна нулю:
3. При одном из аргументов, равном , функция распределения системы превращается в функцию распределения случайной величины, соответствующей другому аргументу:
4. Если оба аргумента равны , функция распределения системы равна единице:
Для системы двух случайных величин можно поставить задачу о вероятности попадания случайной точки (X,Y) в некоторую область на плоскости X0Y. Чтобы упростить задачу, будем рассматривать область в виде прямоугольника: (рис.59):
Тут вы можете оставить комментарий к выбранному абзацу или сообщить об ошибке.
Источник
Двумерный случайный вектор
Основные числовые характеристики дискретной случайной величины. Свойства математического ожидания. Исследование двумерного дискретного случайного вектора. Частные распределения по компонентам и их характеристики. Ковариационная и корреляционная матрицы.
| Рубрика | Математика |
| Вид | курсовая работа |
| Язык | русский |
| Дата добавления | 28.12.2017 |
| Размер файла | 390,2 K |
Отправить свою хорошую работу в базу знаний просто. Используйте форму, расположенную ниже
Студенты, аспиранты, молодые ученые, использующие базу знаний в своей учебе и работе, будут вам очень благодарны.
Размещено на http://www.allbest.ru/
«Московский Авиационный Институт (национальный исследовательский университет)» (МАИ)
«Теория вероятностей и математическая статистика»
Тема: Двумерный случайный вектор
Преподаватель: Степанян Карен Вартанович
Студент: Мищенко Вадим Владимирович
Краткие теоретические сведения
Основные числовые характеристики дискретной случайной величины.
Основными характеристиками ДСВ являются математическое ожидание, дисперсия и среднеквадратическое отклонение.
Характеристикой среднего значения случайной величины служит математическое ожидание.
Математическим ожиданием дискретной случайной величины называют сумму произведений всех ее возможных значений на их вероятности:
Свойства математического ожидания:
1. Математическое ожидание постоянной величины равно самой постоянной:
2. Константу можно выносить за знак математического ожидания:
3. Математическое ожидание произведения взаимно независимых случайных величин равно произведению математических ожиданий сомножителей:
4. Математическое ожидание суммы случайных величин равно сумме математических ожиданий слагаемых:
(для разности аналогично)
Характеристиками рассеяния возможных значений случайной величины вокруг математического ожидания служат, в частности, дисперсия и среднее квадратическое отклонение.
Начальными и центральными моментами порядка r непрерывной СВ X называются числа
Центральный момент второго порядка называется дисперсией СВ X и обозначается как dx?D[X]? .Дисперсия dx характеризует степень рассеивания реализаций СВ X около ее МО.Дисперсию удобно вычислять по формуле:
двумерный дискретный случайный вектор
1. Дисперсия постоянной равна нулю:
2. Постоянный множитель можно выносить за знак дисперсии, предварительно возведя его в квадрат:
3. Дисперсия суммы двух случайных величин равно:
Средним квадратическим отклонением случайной величины называют квадратный корень из дисперсии:
Этап I. Исследование двумерного дискретного случайного вектора.
Таблица распределения случайного вектора задана следующим образом
1. По заданному совместному распределению найти частные распределения компонент и , а также их основные числовые характеристики: математическое ожидание, дисперсию, среднеквадратическое отклонение.
2. Построить график двумерной функции распределения.
3. Выяснить, являются ли компоненты вектора зависимыми. Если зависимы, то построить новый вектор с теми же частными распределениями, но независимыми компонентами.
4. Для обоих (если разные) векторов записать вектор математического ожидания, построить ковариационную и корреляционную матрицу.
5. Вычислить условные распределения в сечениях и найти соответствующие условные математические ожидания в сечениях; записать H(x) и G(y) как неслучайные функции заданные на множестве точек.
6. Построить наилучшие в среднеквадратичном оценку величины по и оценку величины по .
7. Проверить выполнения формулы полного математического ожидания для обеих оценок.
8. Найти точность оценивания для обеих оценок: и .
9. Найти точность оценивания для тривиальных оценок: и
.
10. Сравнить полученные в последних двух пунктах точности.
Расчетная часть по этапуI.
Таблица распределения случайного вектора
1. Частные распределения по компонентам и их основные числовые характеристики.
Находим ряды распределения X и Y.
Пользуясь формулой ?P(xi,yj) = pi (j=1..n), находим ряд распределения X.
Математическое ожидание M[]:
M[] =? xiPi= (-3)*0.5 + 0*0.1/6 + 3*1/3 = -0.5
Для нахождения дисперсии найдем второй начальный момент:
M[]? =? xi?Pi= (-3)?*0.5 + 0?*0.1/6 + 3?*1/3= 7.5
Среднее квадратическое отклонение ?(x):
Пользуясь формулой ?P(xi,yj) = qj (i=1..m), находим ряд распределения Y.
Математическое ожидание M:
M= 6*0.4 + 14*0.6 = 10.8
Для нахождения дисперсии найдем второй начальный момент:
M? =? yi?Pi=6?*0.4 + 14?*0.6 = 132
D= 62*0.4 + 142*0.6 — 10.82 = 15.36
Среднее квадратическое отклонение ?(y):
Поскольку, P(X=-3,Y=6) = 0.2=0.5*0.4, то случайные величины X и Y независимы. Исследование компонент и случайного вектора на независимость.
Если и являются независимыми компонентам, тогда должно выполняться равенство
следовательно, компоненты и являются независимыми.
Смешанные моменты 2-го порядка, ковариационная и корреляционная матрицы.
cov(X,Y) = M[X*Y] — M[X]*M[Y]
cov(X,Y) = 6*-3*0.2 + 14*-3*0.3 + 6*0*1/15 + 14*0*0.1 + 6*3*2/15 +
+ 14*3*0.2 -0.5 * 10.8 = 0
Если случайные величины независимы, то их ковариации равна нулю.
Коэффициент корреляции: r=0
Вычисление условных распределений в сечениях
Условный закон распределения X(Y=6):
P(X=-3/Y=6) = 0.2/0.4 = 0.5
P(X=0/Y=6) = 1/15*5/2= 1/6
P(X=3/Y=6) = 2/15*5/2 =4/3
Условное математическое ожидание M[X/Y=6):
M[X/Y=y] = (-3)*0.5 + 0*1/6 + 3*1/3 = -0.5
Условный закон распределения X(Y=14):
P(X=-3/Y=14) = 0.3/0.6 = 0.5
P(X=0/Y=14) = 0.1/0.6 = 1/6
P(X=3/Y=14) = 0.2/0.6 = 1/3
Условное математическое ожидание M[X/Y=14):
M[X/Y=y] = (-3)*0.5 + 0*1/6+ 3*1/3 = -0.5
Условный закон распределения Y(X=-3):
P(Y=6/X=-3) = 0.2/0.5 = 0.4
P(Y=14/X=-3) = 0.3/0.5 = 0.6
Условное математическое ожидание M[Y/X=-3):
M[Y/X=x] = 6*0.4 + 14*0.6 = 10.8
Условный закон распределения Y(X=0):
P(Y=6/X=0) = 1/15*15/2 = 0.4
P(Y=14/X=0) = 0.1/1/15 = 0.6
Условное математическое ожидание M[Y/X=0):
M[Y/X=x] = 6*0.4 + 14*0.6 = 10.8
Условный закон распределения Y(X=3):
P(Y=6/X=3) = 1/6/1/3 = 0.4
P(Y=14/X=3) = 0.2/1/3 = 0.6
Условное математическое ожидание M[Y/X=3):
M[Y/X=x] = 6*0.4 + 14*0.6 = 10.8
Запишем функции H(x) и G(y) как неслучайные функции заданные на множестве точек
Построениенаилучших оценок величины по , величины по .
Условное мат. ожиданиеявляется наилучшей среднеквадратичной оценкой одной величины от другой.
Проверка выполнения формулы полного математического ожидания.
Этап II. Расчет вероятности попадания случайного вектора в заданную область.
Требуется найти вероятность попадания двумерного гауссовского случайного вектора в область состоящую из двух прямоугольников. Координаты прямоугольников заданы в формате (левый, верхний, правый, нижний):
2ой (0.3, 1.8, 1.1, 0.5)
Компоненты гауссовского вектора некоррелированы.
Расчетная часть по этапу II.
Графическое изображение заданной области.
Вероятность попадания двумерного гауссовского случайного вектора в область, состоящую из прямоугольников D1 и D2равна сумме вероятностей попадания случайного вектора в каждый из прямоугольников.
Если СВ некоррелированы, то в случае нормального распределения они будут независимыми (доказательства в этой работе приводится не будут). Тогда получаем:
Центр рассеивания находится в точке (1.1, -1,6) и плотность вероятности двумерного вектора будет иметь следующий вид
Тогда вероятность попадания случайного вектора в прямоугольник, ограниченный прямыми x=a, x=b, y=c, y=d,при условии независимости компонент, выражается так
Рассчитаем вероятность попадания вектора в каждый из прямоугольников:
Эту задачу можно интерпретировать как вычисление вероятности поражения цели, состоящую из двух заданных в условии прямоугольников, при стрельбе. Характеристиками средств поражения являются область (эллипс) рассеивания с центром (1.1, -1,6) и среднеквадратические отклонения =2,=4.Вероятность поражения целей в данном случае составит .
Cписок иcпользованной литературы
1. Кибзун А. И., Горяинова Е. Р., Наумов А. В., Сиротин А. Н. «Теория вероятностей и математическая статистика. Базовый курс с примерами и задачами»;
2. Т. А. Матвеева, В. Б. Светличная, С. А. Зотова «Теория вероятностей:системы случайных величин и функции случайных величин»;
3. Буре В.М., Грауэр Л.В. «ШАД» Санкт-Петербург, 2013;
4. Пискунов Н. С. «Дифференциальное и интегральное исчисления для втузов», т. 2: Учебное пособие для втузов.—13-е изд.— М.: Наука, Главная редакция физико-математической литературы, 1985;
5. Вентцель Е. С. Элементарный курс теории вероятностей в применении к задачам стрельбы и бомбометания. — М.: Военная Воздушная Краснознаменная ордена Ленина академия им. Жуковского, 1945.
6. Вентцель Е. С. Теория вероятностей 4-е изд. — М.: Наука, 1969. — 576 c.
7. Вентцель Е. С., Овчаров Л. А. Теория вероятностей: Задачи и упражнения. М.: Наука, 1969.
8. Вентцель Е.С., Овчаров Л. А. Прикладные задачи теории вероятностей. 1983. — 416 c.
Размещено на Allbest.ur
Подобные документы
Рассмотрение в теории вероятностей связи между средним арифметическим и математическим ожиданием. Основные формулы математического ожидания дискретного распределения, целочисленной величины, абсолютно непрерывного распределения и случайного вектора.
презентация [55,9 K], добавлен 01.11.2013
Особенности функции распределения как самой универсальной характеристики случайной величины. Описание ее свойств, их представление с помощью геометрической интерпретации. Закономерности вычисления вероятности распределения дискретной случайной величины.
презентация [69,1 K], добавлен 01.11.2013
Определение вероятностей различных событий по формуле Бернулли. Составление закона распределения дискретной случайной величины, вычисление математического ожидания, дисперсии и среднеквадратического отклонения случайной величины, плотностей вероятности.
контрольная работа [344,8 K], добавлен 31.10.2013
Определение вероятности для двух несовместных и достоверного событий. Закон распределения случайной величины; построение графика функции распределения. Нахождение математического ожидания, дисперсии, среднего квадратичного отклонения случайной величины.
контрольная работа [97,1 K], добавлен 26.02.2012
Теория вероятностей и закономерности массовых случайных явлений. Неравенство и теорема Чебышева. Числовые характеристики случайной величины. Плотность распределения и преобразование Фурье. Характеристическая функция гауссовской случайной величины.
реферат [56,1 K], добавлен 24.01.2011
Источник