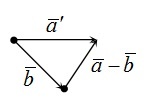- Сложение и вычитание векторов
- Сумма векторов. Сложение векторов. Правило треугольника
- Разность векторов. Вычитание векторов
- Умножение вектора на число
- Вычитание векторов. Как найти разность векторов
- Откладывание вектора от данной точки
- Вычитание векторов. Правило первое
- Готовые работы на аналогичную тему
- Вычитание векторов. Правило второе
- Пример задачи на понятие разности векторов
- Вычитание векторов
- Как происходит вычитание векторов
- Как производится вычитание векторов по координатам
- Основные правила вычисления
- Правило треугольника
- Правило параллелограмма
- Примеры задач на понятие разности векторов
- Сумма и разность векторов
- Сумма векторов
- Формула сложения векторов
- Формула вычитания векторов
Сложение и вычитание векторов
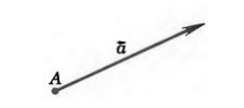
Теорема 1 От любой точки \( K \) можно отложить вектор единственный \( \overrightarrow \) .
Существование: Имеем два следующих случая:
Здесь получаем, что искомый нами вектор совпадает с вектором \( \overrightarrow
Из данного выше построения сразу же будет следовать единственность данного вектора.
Сумма векторов. Сложение векторов. Правило треугольника
Сложение векторов выполняется по правилу треугольника или по правилу параллелограмма.
Суммой нескольких векторов \( \vec
Такая операция выполняется по правилу многоугольника.
Сумма векторов в координатах
При сложении двух векторов соответствующие координаты складываются.
\( \vec + \vec = \left( <
Отметим несколько свойств сложения двух векторов:
Для произвольного вектора \( \overrightarrow \) выполняется равенство
Для произвольных точек \( A,\ B\ и\ C \) справедливо следующее равенство
Замечание Таким способом также можно строить сумму любого числа векторов. Тогда оно будет носить название правила многоугольника.
Разность векторов. Вычитание векторов
Разность двух одинаковых векторов равна нулевому вектору :
\( \vec — \vec = \vec <0>\)
Длина нулевого вектора равна нулю:
\( \left| \vec <0>\right| = 0 \)
Разность векторов в координатах
При вычитании двух векторов соответствующие координаты также вычитаются.
\( \vec — \vec = \left( <
Умножение вектора на число
Пусть нам дан вектор \( \overrightarrow
Определение Произведением вектора \( \overrightarrow
Длина вектора \( \overrightarrow
Векторы \( \overrightarrow
Обозначение: \( \ \overrightarrow
Источник
Вычитание векторов. Как найти разность векторов
Вы будете перенаправлены на Автор24
Откладывание вектора от данной точки
Для того, чтобы ввести разность векторов, сначала необходимо разобраться в таком понятии, как откладывание вектора от данной точки.
Введем следующую теорему:
От любой точки $K$ можно отложить вектор $\overrightarrow$ и притом только один.
Доказательство.
Существование: Здесь нужно рассмотреть два случая:
В этом случае, очевидно, что искомый вектор — вектор $\overrightarrow
Рисунок 2. Иллюстрация теоремы 1
Единственность: единственность сразу следует из построения, проведенного в пункте «существование».
Теорема доказана.
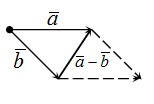
Вычитание векторов. Правило первое
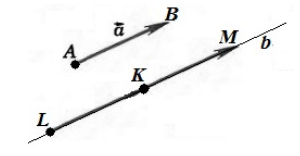
Пусть нам даны векторы $\overrightarrow$ и $\overrightarrow$.
Готовые работы на аналогичную тему
Построение разности двух векторов рассмотрим с помощью задачи.
Решение.
Рисунок 3. Разность двух векторов
По правилу треугольника для построения суммы двух векторов видим, что
Из определения 2, получаем, что
Вычитание векторов. Правило второе
Вспомним следующее необходимое нам понятие.
Вектор $\overrightarrow
Для того чтобы ввести второе правило для разности двух векторов, нам необходимо в начале ввести и доказать следующую теорему.
Доказательство.
По определению 2, имеем
Прибавим к обеим частям вектор $\left(-\overrightarrow\right)$, получим
Так как векторы $\overrightarrow$ и $\left(-\overrightarrow\right)$ противоположны, то $\overrightarrow+\left(-\overrightarrow\right)=\overrightarrow<0>$. Имеем
Теорема доказана.
Пример задачи на понятие разности векторов
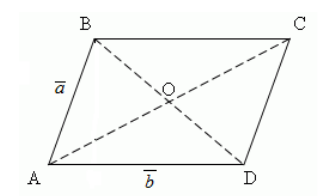
Рисунок 4. Параллелограмм
Решение.
а) Произведем сложение по правилу треугольника, получим
Из первого правила разности двух векторов, получаем
б) Так как $\overrightarrow
По теореме 2, имеем
Используя правило треугольника, окончательно имеем
Источник
Вычитание векторов
Как происходит вычитание векторов
Вычитание векторов — это арифметическое действие в геометрии, при котором из одного вектора отнимают другой.
Чтобы вычесть \(\overrightarrow b\) из \(\overrightarrow а\) , нужно найти такой \(\overrightarrow с\) , сложение которого с вектором \(\overrightarrow b\) составляло бы \(\overrightarrow а\) .
Таким образом, формула разности будет выглядеть так:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
\(\overrightarrow а-\overrightarrow b=\overrightarrow а+\left(-\overrightarrow b\right)\)
Если задан \(\overrightarrow а\) , то можно построить противоположный ему \(-\overrightarrow а\) , равный по длине, но противоположно направленный. Тогда происходит сведение двух противоположно направленных векторов к нулевому:
\(\overrightarrow а+\left(-\overrightarrow а\right)=0\)
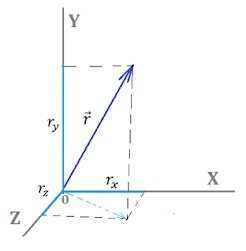
Как производится вычитание векторов по координатам
Если необходимо произвести вычитание векторов по координатам, то следует просто вычесть соответствующие точки. То есть если из \(\overrightarrow а\) отнимается \(\overrightarrow b\) , то из X1 отнимаем X2, из Y1 Y2 и из Z1 Z2.
Проиллюстрируем координатное пространство:
Основные правила вычисления
Для того, чтобы найти значение разности векторов, можно использовать несколько способов.
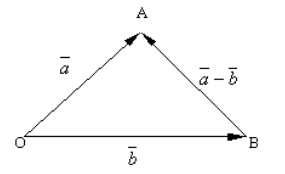
Правило треугольника
Чтобы графически продемонстрировать разность, необходимо отложить от произвольной точки вектор \(\overrightarrow а\) , из его начала \(\overrightarrow b\) . Тогда вектор, начало которого совпадает с концом \( \overrightarrow b\) , а конец — с концом \(\overrightarrow a\) , и будет искомым вектором разности \(\overrightarrow a\;-\;\overrightarrow b\) . Проиллюстрируем это:
Правило параллелограмма
Если два неколлинеарных, то есть непараллельных вектора \(\overrightarrow а\) и \(\overrightarrow b\) имеют общее начало, то их разностью является вектор, совпадающий с диагональю параллелограмма, построенного на \(\overrightarrow а\) и \(\overrightarrow b\) , причем начало этой диагонали совпадает с концом \(\overrightarrow b\) , а конец — с концом \(\overrightarrow а\) .
Если векторы \(\overrightarrow а\) и \(\overrightarrow b\) заданы в некотором промежутке:
\(\overrightarrow a=\left(а_1;а_2\right),\;\overrightarrow b=\left(b_1;b_2\right)\)
то, чтобы найти координаты их разности \(\overrightarrow a\;-\;\overrightarrow b\) , необходимо от точек \(\overrightarrow a\) отнять соответствующие точки \(\overrightarrow b\) :
\(\overrightarrow a\;-\;\overrightarrow b=\left(a_1;a_2\right)-\left(b_1;b_2\right)=\left(a_1-b_1;a_2-b_2\right)\)
Проиллюстрируем правило многоугольника:
Примеры задач на понятие разности векторов
Задача 1
Дано
\(\overrightarrow a\;=\left(2;-1\right),\;\overrightarrow b=\left(0;2\right)\)
Найти: \(\overrightarrow с=2\overrightarrow a-3\overrightarrow b\;\)
Решение
Найдем координаты \(2\overrightarrow a\) и \(3\overrightarrow b\) . Для этого умножим каждую на два и три:
\(2\overrightarrow а=2\times\left(2;-1\right)=\left(2\times2;2\times\left(-1\right)\right)=\left(4;-2\right), 3\overrightarrow b=3\times\left(0;2\right)=\left(3\times0;3\times2\right)=\left(0;6\right)\)
Тогда искомый вектор:
\(\overrightarrow с=2\overrightarrow a-3\overrightarrow b=\left(4;-2\right)-\left(0;6\right)=\left(4-0;\;-2-6\right)=\left(4;-8\right)\)
Ответ: \(\overrightarrow с=\left(4;-8\right).\)
Задача 2
Дано
Найти: координаты \(\overrightarrow
Решение
Для начала найдем проекции \(\overrightarrow
Для этого от координат конца вектора, то есть точек B и D, нужно отнять соответствующие проекции его начала, то есть точек А и С.
Тогда для нахождения координат разности \(\overrightarrow
Источник
Сумма и разность векторов
В данной публикации мы рассмотрим, как найти сумму и разность векторов, приведем геометрическую интерпретацию, а также формулы, свойства и примеры этих действий.
Сумма векторов
Сложение векторов выполняется по правилу треугольника.
Геометрическая интерпретация:
Суммой a и b является вектор c , начало которого совпадает с началом a , а конец – с концом b . При этом конец вектора a должен совпадать с началом вектора b .
Для сложения векторов также используется правило параллелограмма.
Два неколлинеарных вектора a и b можно привести к общему началу, и в этом случае их суммой является вектор c , совпадающий с диагональю параллелограмма и берущий начало в той же точке, что и исходные векторы.
Формула сложения векторов
Элементы вектора c равняются попарной сумме соответствующих элементов a и b .
| Для плоских задач | Для трехмерных задач | Для n-мерных векторов |  Если из вектора a вычесть b , то получится c , причем должно соблюдаться условие: Формула вычитания векторовЭлементы вектора c равны попарной разности соответствующих элементов a и b .
|