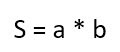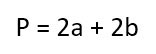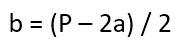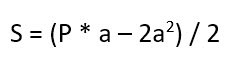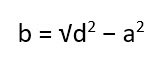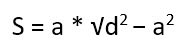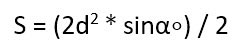Два способа нахождения площади прямоугольника

Как найти площадь прямоугольника – 9 способов с формулами и примерами

Самый простой способ – перемножить две стороны. Но иногда эти две стороны неизвестны.

Умножьте его ширину на высоту. Это самый простой способ найти площадь прямоугольника. Например, если ширина прямоугольника равна 4 см, а высота – 2 см, то площадь будет равна 4*2 = 8 см.

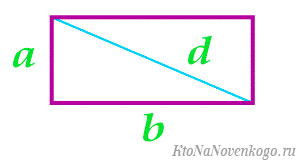
По диагонали и стороне

Должна быть известна диагональ и любая из сторон. Действия:

1. Найти квадрат диагонали, то есть умножить ее на саму себя.
2. Найти квадрат известной стороны.
3. Из квадрата диагонали вычесть квадрат стороны.
4. Найти квадратный корень получившейся разности.
5. Умножить его на известную сторону.

Пример. Сторона прямоугольника равна 3 см, а диагональ – 5 см. Найдите площадь.

1. Квадрат стороны = 3*3 = 9 см.
2. Квадрат диагонали = 5*5 = 25 см.
3. Вычитаю из квадрата диагонали квадрат стороны: 25-9 = 16 см.
4. Нахожу квадратный корень получившейся разности. Корень из 16 = 4 см.
5. Умножаю корень разности на известную сторону: 16*9 = 144 см.

Диагональ в прямоугольнике – это гипотенуза, потому что она всегда находится напротив угла в 90 градусов. Найти диагональ можно по формуле нахождения гипотенузы, например, поделив катет угла A на синус угла A.

По стороне и диаметру описанной окружности

Вокруг любого прямоугольника можно описать окружность. Вам надо знать диаметр этой окружности и любую из сторон прямоугольника.

1. Найдите квадрат диаметра – умножьте диаметр на диаметр.
2. Найдите квадрат известной стороны.
3. Отнимите от квадрата диаметра квадрат стороны.
4. Найдите квадратный корень разности.
5. Умножьте квадратный корень на известную сторону.

Пример. Найдите площадь прямоугольника, если диаметр описанной окружности равен 10 см, а одна из сторон равна 8 см.

1. Квадрат диаметра: 10*10 = 100 см.
2. Квадрат стороны: 8*8 = 64 см.
3. Отнимаю от квадрата диаметра квадрат стороны: 100-64 = 36 см.
4. Квадратный корень из 36 равен 6 см (потому что 6*6 = 36).
5. Умножаю сторону на корень из разности: 8*6 = 48 см.

Диаметр описанной окружности всегда равен диагонали прямоугольника. Смотрите:

А найти диагональ можно по формуле гипотенузы прямоугольного треугольника.

Диаметр равен двум радиусам, потому что радиус – это половина диаметра.

По радиусу описанной окружности и стороне

Можно просто найти диаметр (умножить радиус на два) и использовать формулу выше.

1. Найти квадрат радиуса (умножьте радиус на радиус).
2. Умножить квадрат радиуса на 4.
3. Найти квадрат известной стороны.
4. Отнять от четырех радиусов в квадрате квадрат известной стороны (из второго отнять третье).
5. Найти квадратный корень разности.
6. Умножить корень на известную сторону.

Пример. Найдите площадь прямоугольника, если радиус описанной окружности равен 5 см, а одна из сторон равна 6 см.

1. Квадрат радиуса: 5*5=25 см.
2. Четыре квадрата радиуса: 4*25 = 100 см.
3. Квадрат стороны: 6*6 = 36 см.
4. Отнимаю от четырех радиусов в квадрате квадрат стороны: 100-36 = 64 см.
5. Нахожу квадратный корень разности. Корень из 64 равен 8 см.
6. Умножаю корень на сторону: 8*6 = 48 см.

Радиус = половине диаметра.

Радиус = половине гипотенузы прямоугольного треугольника, вокруг которого описана окружность. Потому что эта гипотенуза = диагонали прямоугольника = диаметру.

По стороне и периметру – 1 способ

Периметр – это сумма всех сторон прямоугольника. P=a+b+a+b. Другая формула периметра: P=2(a+b).

Если известен периметр и одна сторона, надо найти вторую сторону и перемножить их.

Пример. Периметр прямоугольника равен 14 см, а одна из сторон равна 3 см. Найдите площадь.

1. Нахожу вторую сторону прямоугольника:
   1. P=2(a+b).
   2. P=2a+2b.
   3. 14= 2*3+2b.
   4. 14 = 6+2b.
   5. 2b = 14-6 = 8.
   6. b = 8/2.
   7. b = 4.
2. Нахожу площадь по основной формуле. S = 3*4 = 12 см.

По стороне и периметру – 2 способ

1. Умножьте периметр на сторону.
2. Найдите квадрат стороны.
3. Умножьте квадрат стороны на 2.
4. Отнимите от произведения периметра и стороны два квадрата стороны (от первого отнимите третье).
5. Поделите на 2.

Пример. Сторона прямоугольника равна 8, а периметр равен 28. Найдите площадь.

1. Умножаю периметр на сторону: 8*28 = 224 см.
2. Нахожу квадрат стороны: 8*8 = 64 см.
3. Умножаю квадрат стороны на два: 64*2 = 84 см.
4. Отнимаю из первого третье: 224-84 = 140 см.
5. Делю разность на два: 140/2 = 70 см.

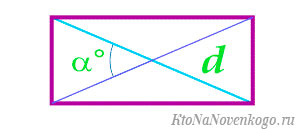
По диагонали и углу между диагоналями

Диагонали прямоугольника всегда равны.

1. Найти квадрат диагонали (умножить диагональ на саму себя).
2. Найти половину этого квадрата – умножить его на 0,5.
3. Найти синус угла между диагоналями.
4. Умножить половину квадрата диагонали на синус угла между диагоналями.

Пример. Найдите площадь прямоугольника, диагональ которого равна 10 см, а угол между диагоналями – 30 градусов.

1. Квадрат диагонали: 10*10 = 100 см.
2. Половина этого квадрата: 0,5*100 = 50 см.
3. Синус угла между диагоналями: sin 30 градусов = 0,5.
4. Перемножаю половину квадрата и синус угла, чтобы найти площадь: 50*0,5 = 25 см.

Вот еще вам таблица основных значений из тригонометрии. Там как раз отмечено, что синус 30 градусов всегда равен 0,5 (1/2).

По радиусу описанной окружности и углу между диагоналями – первый способ

Радиус описанной окружности равен половине ее диаметра, а диаметр равен диагонали прямоугольника. Надо найти диаметр и посчитать площадь по формуле выше.

Пример. Найдите площадь прямоугольника, если радиус описанной окружности равен 6 см, а угол между диагоналями – 30 градусов.

1. Находим длину диагонали: 6*2 =12 см.
2. Квадрат диагонали равен 144 см.
3. Половина квадрата: 72 см.
4. Синус 30 градусов равен 0,5.
5. Умножаем половину квадрата на синус: 72*0,5 = 36 см.

По радиусу описанной окружности и углу между диагоналями – второй способ

1. Найти квадрат радиуса (умножить радиус на радиус).
2. Умножить квадрат радиуса на два.
3. Найти синус угла между диагоналями.
4. Умножить синус угла на два радиуса в квадрате.

Пример. Найдите площадь прямоугольника, если радиус описанной окружности равен 6, а угол между диагоналями – 30 градусов.

1. Квадрат радиуса: 6*6 = 36.
2. Два радиуса в квадрате: 36*2 = 72.
3. Синус 30 градусов равен 0,5.
4. Произведение синуса и двух радиусов в квадрате: 72*0,5 = 36 см.

Покритикуйте статью и стиль подачи материала в комментариях, я внесу правки. Это моя вторая статья по математике, я хочу, чтобы они все были образцовыми.

Источник

Площадь прямоугольника

Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru.

Сегодня мы расскажем, как вычислять площадь прямоугольника.

Различные формулы вычисления площади (а их действительно немало), изучают в 8 классе школы.

Что такое площадь прямоугольника

Но для начала давайте все-таки дадим основные определения:

Прямоугольник – это геометрическая фигура, относящаяся к категории четырехугольников. Ее отличительная особенность в том, что противоположные стороны лежат на параллельных прямых (то есть параллельны друг другу) и равны.

А частным случаем прямоугольника, если у него все стороны равны между собой, является квадрат.

Площадь любой геометрической фигуры, формально говоря, это ее размер. Другими словами, размер того пространства, которое находится внутри границ фигуры.

В отношении четырехугольников применимо еще понятие «квадратура». С его помощью показывали, сколько квадратов вместится внутрь фигуры.

Собственно, отсюда и пошло современное обозначение площадей, когда речь идет о габаритах помещения или какой-то территории. Мы часто слышим «столько-то квадратных метров (миллиметров, сантиметров, километров)» или просто «столько-то квадратов».

Для площади геометрических фигур действуют определенные правила:

1. Она не может быть отрицательной.
2. У равных фигур всегда равные площади.
3. Если две фигуры не пересекаются друг с другом, то их общая площадь равна сумме площадей фигур по отдельности.
4. Если одна фигура вписана в другую, то ее площадь всегда меньше, чем у второй.

» alt=»»>

Обычно фигуры, которые имеют равные площади, называют « равновеликими».

Как найти площадь прямоугольника

Площадь прямоугольника вычисляется по очень простой формуле – надо лишь перемножить его стороны.

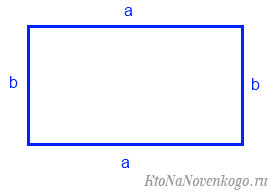
Возьмем, к примеру, такой прямоугольник:

Площадь геометрической фигуры обычно обозначается латинской буквой «S». И тогда формула для конкретного примера будет:

Например, если мы имеем прямоугольник со сторонами 2 и 3 сантиметра, то его площадь составит 2 * 3 = 6 сантиметров.

Но бывают случаи, когда неизвестны размеры сторон прямоугольника, а площадь вычислить все равно надо. Для этого существуют более сложные формулы.

Формула площади прямоугольника через периметр

Если известна длина только одной стороны, но известен еще и периметр прямоугольника.

В этом случае есть два варианта.

Первый — вычислить длину второй стороны. Для этого надо вспомнить, что периметр (обозначается буквой «Р») считается по формуле:

И тогда обратные расчеты выглядят вот так:

Площадь прямоугольника через диагональ

Известна одна сторона и длина диагонали.

Тут опять же есть два варианта. В первом случае вычисляем длину второй стороны, используя теорему Пифагора.

Второй вариант – опять же сразу прибегнуть к готовой формуле:

Если известны длина диагоналей и угол между ними.

В этом случае стоит воспользоваться вот такой формулой:

Вот и все, что нужно знать о вычислении площади прямоугольников.

Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru

Эта статья относится к рубрикам:

Комментарии и отзывы (1)

Смех смехом, но я встречал довольно много людей, которые не могли высчитать площадь прямоугольника! Причем люди эти были с высшим образованием, выпускники технического ВУЗа. Вот так люди замечательно учатся!

Источник

Урок 27 Бесплатно Площадь. Площадь прямоугольника

В нашей жизни приходится часто вычислять площади различных геометрических фигур. Например, площадь огорода, поля; при покупке жилья — площадь квартиры, дома, комнат; делая ремонт, мы вычисляем площадь стен, пола, окон, строительных материалов и т.д.

Сегодня мы научимся вычислять площади двух геометрических фигур: прямоугольника и квадрата, познакомимся с понятием площади и единицами ее измерения.

Выясним, какими свойствами обладает площадь.

Разберем несколько примеров решения задач.

Площадь плоских геометрических фигур

Прямоугольник, квадрат и другие замкнутые геометрические фигуры имеют некоторую границу (контур), которая делит плоскость на области: область, которая находится снаружи этой границы, и область, которая находится внутри контура.

Площадью называют часть плоскости, ограниченную линией (кривой или ломаной).

Для обозначения площади обычно используют заглавную латинскую букву S.

Площадь различных фигур можно сравнивать.

Площадь будет больше у той фигуры, которая на плоскости занимает больше места.

Например, даны три фигуры №1, №2, №3.

Площадь фигуры №1 больше площади фигуры №2 и №3, а площадь фигуры №2 больше площади фигуры №3.

Невооруженным глазом заметно, какая фигура меньше, а какая больше.

Рассмотрим еще один пример.

Даны две фигуры №1 и №2.

Однозначно сказать, площадь какой фигуры больше, а какой меньше, затруднительно.

Нам известно, что фигуры называют равными, если при наложении одной фигуры на другую они совпадают.

Попробуем сравнить первую и вторую фигуры наложением.

Этот способ сравнения не смог дать нам однозначного ответа, поэтому постараемся найти более точный способ нахождения площади данных фигур.

Известно, чтобы определить длину отрезка, его сравнивают с отрезком, принятым за единицу измерения.

В таком случае, чтобы измерить площадь фигуры, необходимо посчитать сколько раз в ней помещается другая фигура, принятая за единицу измерения.

При измерении длины отрезка используют линейные меры длины: 1 мм, 1 см, 1 дм и т.д.

Площадь же измеряют квадратными единицами.

Квадратная единица представляет собой квадрат, стороны которого выражены линейными единицами; другими словами, площадь измеряется квадратными единицами длины.

Квадрат, у которого все стороны равны 1 мм, называется квадратным миллиметром.

Квадрат, у которого все стороны равны 1 см, называется квадратным сантиметром.

Квадрат, у которого все стороны равны 1 дм, называется квадратным дециметром.

Аналогично определяется квадратный метр и квадратный километр.

Определить площадь фигуры- это значит найти сколько квадратных единиц содержится в данной фигуре.

Обозначают квадратные единицы следующим образом:

1 мм 2 — один миллиметр квадратный (квадратный миллиметр)

1 см 2 — один сантиметр квадратный (квадратный сантиметр)

1 дм 2 — один дециметр квадратный (квадратный дециметр)

1 м 2 — один метр квадратный (квадратный метр)

1 км 2 — один километр квадратный (квадратный километр) и т.д.

Если разбить фигуру на n равных квадратов, то ее площадь будет равна n квадратных единиц.

Найдем для нашего примера площадь фигуры №1 и площадь фигуры №2 и сравним полученные площади. Так мы сможем выяснить, какая из фигур имеет большую площадь.

Для этого разобьем эти две фигуры на одинаковые квадраты со сторонами 1 см (т.е. на квадратные сантиметры).

Фигура №1 состоит из 12 квадратов, следовательно, данная фигура имеет площадь 12 квадратных единиц, в нашем случае квадратных сантиметров: S₁ = 12 см 2

Фигура №2 состоит также из 12 квадратов, значит, данная фигура имеет площадь 12 квадратных единиц, в нашем случае квадратных сантиметров: S₂ = 12 см 2

Сравним площади фигур: так как S₁ = 12 см 2 и S₂ = 12 см 2 , значит, площади фигур №1 и №2 равны.

У меня есть дополнительная информация к этой части урока!

В каждом конкретном случае необходимо оценивать, в каких единицах измерения удобней выражать площадь той или иной фигуры.

Если требуется определить площадь фигуры, изображенной на листе бумаги, то целесообразнее измерять площадь в квадратных сантиметрах (см 2 ).

Если же необходимо измерить площадь стены или потолка в комнате, то удобно площадь выражать в квадратных метрах (м 2 ).

Большие значения площадей, такие как площадь Земли, островов, континентов, океанов, государств удобнее выражать в квадратных километрах (км 2 ).

Пройти тест и получить оценку можно после входа или регистрации

Площадь прямоугольника и квадрата

Во всех выше рассмотренных примерах мы имели дело с плоскими геометрическими фигурами (прямоугольником и квадратом).

Вспомним, что называют прямоугольником, а что квадратом.

Прямоугольник- это плоская геометрическая фигура, образованная замкнутой ломаной линией, состоящей из четырех звеньев, и плоскостью, которая располагается внутри этой линии.

У прямоугольника противоположные стороны равны и все четыре угла одинаковые.

Обычно прямоугольник обозначают четырьмя заглавными латинскими буквами, записывая их по порядку следования.

Пример: прямоугольник АВDС

Отрезки АВ, ВD, DC, СА называются сторонами прямоугольника АВDС.

Причем АВ = СD и АС = ВD.

Точки А, В, С, D называют вершинами прямоугольника АВDС.

Углы, образованные сторонами АС и АВ, АВ и ВD, ВD и DC, DC и СА, называют углами прямоугольника АВDС.

Отрезки СВ и АD, соединяющие вершины С и В, А и D, — это диагонали прямоугольника АВDС.

В любом прямоугольнике можно провести две диагонали, и они будут равны СВ = АD.

Диагонали пересекаются в точке пересечения диагоналей (точка О— точка пересечения диагоналей СВ и АD).

Она делит диагонали на равные отрезки:

Точка O делит диагональ СВ на равные отрезки СО и ОB.

Точка O делит диагональ АD на равные отрезки AО и ОD.

Каждая диагональ делит прямоугольник на два равных треугольника.

Диагональ СВ делит прямоугольник АВDС на равные треугольники САВ и СDВ.

Диагональ АD делит прямоугольник АВDС на равные треугольники АСD и АВD.

Квадрат- это прямоугольник, у которого все стороны равны.

Квадрат АВDС.

Отрезки АВ, ВD, DC, СА— называются сторонами квадрата АВDС.

Причем АВ = СD = АС = ВD.

Точки А, В, С, D называют вершинами квадрата АВDС.

Углы, образованные сторонами АС и АВ, АВ и ВD, ВD и DC, DC и СА, называют углами квадрата АВDС.

Отрезки СВ и АD, соединяющие вершины С и В, А и D, — это диагонали квадрата АВDС.

Все свойства прямоугольника характерны и для квадрата.

Чтобы найти площадь прямоугольника, можно разделить его на одинаковые единичные квадраты и сосчитать их количество. Такой способ нахождения площади фигуры мы рассмотрели ранее.

Найдем площадь прямоугольника ABCD.

Прямоугольник ABCD разобьем на квадраты со стороной 1 см, значит в нашем случае единицей измерения площади будет квадратный сантиметр (см 2 ).

Посчитаем сколько раз помещается квадратный сантиметр в фигуру ABCD.

В прямоугольнике ABCD содержится 15 квадратов, следовательно, его площадь равна 15 квадратных сантиметров (15 см 2 ).

Если внимательно посмотреть на прямоугольник ABCD, то можно заметить, что он разбит на 3 строчки и каждая строчка содержит 5 квадратов со сторонами 1 см каждый.

Тогда количество таких квадратов в прямоугольнике ABCD можно определить выражением (3 ∙ 5).

Найдем значение данного выражения:

3 ∙ 5 = 15

Значит площадь прямоугольника ABCD равна 15 см 2 .

Пересчитав по порядку каждый квадратный сантиметр прямоугольника ABCD, мы получили такой же результат.

Этот же прямоугольник можно разбить на 5 полос по 3 квадрата со сторонами 1 см каждый.

Найдем площадь прямоугольника ABCD.

В этом случае площадь прямоугольника ABCD будет определяться выражением (5 ∙ 3).

Как нам уже известно, от перестановки множителей произведение не изменяется:

5 ∙ 3 = 15.

Площадь прямоугольника получается равной 15 см 2 Результат, как мы видим, не изменился.

Важно заметить, что сторона АВ прямоугольника ABCD- это ширина данного прямоугольника (равная 3 см), а сторона ВС — это его длина (равная 5 см).

Таким образом, для того, чтобы найти площадь прямоугольника ABCD, не обязательно разбивать его на квадратные единицы, необходимо просто знать длину и ширину этого прямоугольника.

Правило: чтобы найти площадь прямоугольника, нужно его длину умножить на ширину (в одинаковых единицах).

Единицы измерения длины и ширины должны совпадать.

Если меры не совпадают, их необходимо перевести, т.е. свести к единой единице измерения.

Запишем правило в виде формулы.

Площадь прямоугольника обозначим латинской буквой S, ширину прямоугольника обозначим буквой а, длину буквой b.

Формула площади прямоугольника выглядит так:

Рассмотрим некоторые свойства площади.

1. Площади равных фигур равны.

Периметры таких фигур также равны.

Фигуры, имеющие равные площади называются равновеликими.

У меня есть дополнительная информация к этой части урока!

Не следует путать такие понятия, как периметр и площадь геометрических фигур.

Периметр- это замкнутая ломаная или кривая линия (контур) геометрической фигуры, которая ограничивает внутреннюю область этой фигуры.

По сути, периметр- это длина контура фигуры (для многоугольника это сумма длин всех сторон многоугольника).

Периметр часто обозначают заглавной латинской буквой Р.

Периметр измеряется в линейных единицах длины: мм, см, дм и т.д.

Площадь же- это часть плоскости, которая ограничена периметром.

Площадь измеряется только в квадратных единицах длины: мм 2 , см 2 , дм 2 и т.д.

На рисунке периметр обозначен красной линией, площадь фигуры выделена на рисунке штриховкой.

Р = 2 см + 6 см + 2 см + 6 см = 2 (2 + 6) = 16 (см) периметр фигуры (прямоугольника).

S = 2 см∙ 6 см = 12 (см 2 ) площадь фигуры (прямоугольника)

2. Площадь всей фигуры равна сумме площадей ее частей.

Рассмотрим пример, иллюстрирующий данное свойство.

Разделим прямоугольник ABCD на две части ломаной линией KOMN.

Одна из частей- ABNMОK имеет площадь, равную 10 см 2 .

S₁ = 10 см 2 .

Вторая часть- KОMNCD имеет площадь 8 см 2 .

S₂ = 8 см 2 .

Площадь всего прямоугольника равна сумме его частей:

S = 10 см 2 + 8 см 2 = 18 см 2 .

Вычислив площадь прямоугольника по формуле S = a ∙ b,

где а = АВ = 3 см, b = ВС = 6 см.

S = 3 ∙ 6 = 18 см 2 .

Площадь всей фигуры равна 18 см 2 , такой же результат был получен при сложении площадей двух частей, на которые эта фигура была разделена.

Первое и второе свойства- это основные свойства площадей.

3. Диагональ прямоугольника (квадрата), делит его на два равных треугольника.

Пусть отрезок BD делит прямоугольник ABCD на два равных треугольника:

∆ ABD = ∆ BCD

Сумма площадей каждого треугольника равна площади всего прямоугольника, следовательно, площадь каждого треугольника равна половине площади прямоугольника.

4. Площадь квадрата.

Квадрат- это прямоугольник, у которого все четыре стороны равны.

Изобразим квадрат со стороной 2 см (это выражение означает, что все четыре стороны у квадрата будут 2 см).

Площадь квадрата рассчитывается таким же образом, как и площадь прямоугольника:

S = a ∙ b— произведение длины и ширины прямоугольника.

Известно, что в квадрате все стороны между собой равны, значит, длина квадрата равна ширине этого квадрата.

В таком случае, умножив длину на ширину, получим произведение двух равных по значению множителей, каждый равен длине стороны квадрата (а).

Получаем формулу площади квадрата:

S = a ∙ a

Число, умноженное само на себя, представляет собой квадрат этого числа.

Формула площади квадрата будет выглядеть так:

Число возводится во вторую степень, т.е. возводится в квадрат.

Правило: площадь квадрата равна квадрату его стороны.

Рассмотрим такой пример.

Вычислим площадь квадрата со стороной 4 см.

Решение данной задачи:

Пройти тест и получить оценку можно после входа или регистрации

Решение текстовых задач по теме «Площадь. Площадь прямоугольника (квадрата)»

Теперь, когда нам известны формулы площадей прямоугольника и квадрата и их свойства, рассмотрим решение нескольких задач.

Задача №1

Длина столешницы прямоугольной формы 2 м, а ее ширина 10 дм.

Найдите площадь и периметр столешницы.

Единица измерения ширины столешницы выражена в дециметрах, ее сразу переведем в метры.

Задача №2

Периметр прямоугольного участка земли 80 м, а его длина 30 м.

Чему равна площадь этого участка?

Выясним план решения данной задачи.

Решать задачу будем по действиям.

1. Найдем чему равна половина периметра (Р ÷ 2), т.е. выясним, чему равна сумма двух сторон (ширины и длины) участка.

2. Из полученного значения полупериметра вычтем известное значение длины прямоугольника b; таким образом, мы найдем ширину участка а.

3. Когда будут известны ширина и длина участка, можно будет найти его площадь.

Задача №3

Площадь прямоугольной грядки 7 м 2 , ширина этой грядки 1 м.

Чему равен периметр грядки?

Задача №4

Девочка вырезала прямоугольник, длина которого получилась равной 5 см, а ширина 2 см, и разрезала этот прямоугольник по диагонали, у нее получились два равных треугольника.

Найдите площадь этих треугольников.

План решения у нас будет следующим.

1. Первым делом найдем площадь вырезанного прямоугольника.

2. Диагональ делит прямоугольник на два равных треугольника, значит, площадь одного треугольника будет в два раза меньше площади прямоугольника.

3. Разделив площадь прямоугольника на два, получим площадь треугольника.

У меня есть дополнительная информация к этой части урока!

Вычислить площадь квадрата легко, зная длину стороны:

S = а ∙ а = а 2

Рассмотрим случай, когда длина стороны квадрата не определена, но известна длина диагонали квадрата.

Чтобы рассчитать площадь квадрата на основании длины его диагонали, нужно длину диагонали возвести в квадрат и разделить на два.

В виде формулы данное правило выглядит так:

S = р 2 ÷ 2

S— площадь квадрата

p— длина диагонали

Задача №5

Найдите площадь квадрата, диагональ которого равна 4 см.

Площадь квадрата можно найти, если известен его периметр.

Так как все четыре стороны квадрата равны, периметр квадрата находится по формуле

Р = 4 ∙ а

а- это длина стороны квадрата.

Выразим из этой формулы сторону квадрата, для этого разделим периметр на 4.

а = Р ÷ 4

Зная длину стороны квадрата, можно найти площадь квадрата:

S = а 2 = Р 2 ÷ 4 2 = Р 2 ÷ 16

S = Р 2 ÷ 16

Задача №6

Периметр квадратной песочницы 8 м.

Найдите площадь этой песочницы.

Первый способ: решим данную задачу по действиям.

Второй способ: решим данную задачу с помощью формулы S = Р 2 ÷ 16.

Решая задачу первым и вторым способом, ответ получили одинаковый: площадь песочницы оказалась равной S = 4 (м 2 ).

Попробуем решить обратную задачу: по известной площади квадрата найдем его периметр.

Задача №7

Площадь квадратной комнаты равна 25 м 2 .

Найдите периметр этой комнаты.

Пройти тест и получить оценку можно после входа или регистрации

Заключительный тест

Пройти тест и получить оценку можно после входа или регистрации

Источник