Два отрезка решить двумя способами

В том случае, если разность составит положительное число, значит, первый отрезок длиннее второго на соответствующее количество единиц. Если в результате получено нулевое значение — отрезки равны. А если в ответе отрицательное число, следовательно, второй отрезок длиннее первого.

Вывод

Итак, мы выяснили, как сравнить 2 отрезка. Первый способ указывает только на то, какой из них будет длиннее, а какой — короче, а второй показывает числовое значение разницы в длине.

Источник

Простой алгоритм определения пересечения двух отрезков

Введение

Задача

Даны два отрезка, каждый из которых задан двумя точками: (v11, v12), (v21, v22). Необходимо определить, пересекаются ли они, и если пересекаются, найти точку их пересечения.

Решение

Для начала необходимо определить, пересекаются ли отрезки. Необходимое и достаточное условие пересечения, которое должно быть соблюдено для обоих отрезков следующее: конечные точки одного из отрезков должны лежать в разных полуплоскостях, если разделить плоскость линией, на которой лежит второй из отрезков. Продемонстрируем это рисунком.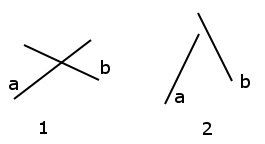

На левом рисунке (1) показаны два отрезка, для обоих из которых условие соблюдено, и отрезки пересекаются. На правом (2) рисунке условие соблюдено для отрезка b, но для отрезка a оно не соблюдается, соответственно отрезки не пересекаются.
Может показаться, что определить, с какой стороны от линии лежит точка — нетривиальная задача, но у страха глаза велики, и всё не так сложно. Мы знаем, что векторное умножение двух векторов даёт нам третий вектор, направление которого зависит от того, положительный или отрицательный угол между первым и вторым вектором, соответственно такая операция антикоммутативна. А так как все вектора лежат на плоскости X-Y, то их векторное произведение (которое обязано быть перпендикулярным перемножаемым векторам) будет иметь ненулевой только компоненту Z, соответственно и отличие произведений векторов будет только в этой компоненте. Причем при изменении порядка перемножения векторов (читай: угла между перемножаемыми векторами) состоять оно будет исключительно в изменении знака этой компоненты.
Поэтому мы можем умножить попарно-векторно вектор разделяющего отрезка на векторы направленные от начала разделяющего отрезка к обеим точкам проверяемого отрезка.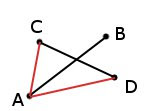

Если компоненты Z обоих произведений будет иметь различный знак, значит один из углов меньше 0 но больше -180, а второй больше 0 и меньше 180, соответственно точки лежат по разные стороны от прямой. Если компоненты Z обоих произведений имеют одинаковый знак, следовательно и лежат они по одну сторону от прямой.
Если один из компонент Z является нулём, значит мы имеем пограничный случай, когда точка лежит аккурат на проверяемой прямой. Оставим пользователю определять, хочет ли он считать это пересечением.
Затем нам необходимо повторить операцию для другого отрезка и прямой, и убедиться в том, что расположение его конечных точек также удовлетворяет условию.
Итак, если всё хорошо и оба отрезка удовлетворяют условию, значит пересечение существует. Давайте найдём его, и в этом нам также поможет векторное произведение.
Так как в векторном произведении мы имеем ненулевой лишь компоненту Z, то его модуль (длина вектора) будет численно равен именно этой компоненте. Давайте посмотрим, как найти точку пересечения.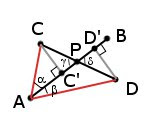

Длина векторного произведения векторов a и b (как мы выяснили, численно равная его компоненте Z) равна произведению модулей этих векторов на синус угла между ними (|a| |b| sin(ab)). Соответственно, для конфигурации на рисунке мы имеем следующее: |AB x AC| = |AB||AC|sin(α), и |AB x AD| = |AB||AD| sin(β). |AC|sin(α) является перпендикуляром, опущенным из точки C на отрезок AB, а |AD|sin(β) является перпендикуляром, опущенным из точки D на отрезок AB (катетом ADD’). Так как углы γ и δ — вертикальные углы, то они равны, а значит треугольники PCC’ и PDD’ подобны, а соответственно и длины всех их сторон пропорциональны в равном отношении.
Имея Z1 (AB x AC, а значит |AB||AC|sin(α) ) и Z2 (AB x AD, а значит |AB||AD|sin(β) ), мы можем рассчитать CC’/DD’ (которая будет равна Z1/Z2), а также зная что CC’/DD’ = CP/DP легко можно высчитать местоположение точки P. Лично я делаю это следующим образом:

Px = Cx + (Dx-Cx)*|Z1|/|Z2-Z1|;
Py = Cy + (Dy-Cy)*|Z1|/|Z2-Z1|;

Вот и все. Мне кажется что это действительно очень просто, и элегантно. В заключение хочу привести код функции, реализующий данный алгоритм. В функции использован самодельный шаблон vector , который является шаблоном вектора размерностью int с компонентами типа typename. Желающие легко могут подогнать функцию к своим типам векторов.

Источник

Как сравнить два отрезка: способы и примеры

Отрезок — часть прямой, ограниченная двумя точками, кратчайшее расстояние между этими точками. Существует несколько способов сравнения геометрических фигур, выбор такого способа зачастую зависит не только от условия задачи, но и от возможностей. Как же сравнивать отрезки, расскажем в этой статье.

• Способы сравнения двух отрезков
• Измерение длины
• Наложение друг на друга
• Сравнение в координатной сетке
• Примеры

Способы сравнения двух отрезков

В геометрии две фигуры, имеющие одинаковый размер и форму, называются равными. Сравнение фигур дает возможность сказать, одинаковы ли они. Одним из способов является наложение. Если фигуры удается совместить наложением, они считаются равными.

Сравнить фигуры — значит, определить, которая из них длиннее или короче. Ответ должен быть определенным, нельзя сказать, что один отрезок длиннее или равен второму. В математике такой ответ неправилен, его можно приравнять к отсутствию ответа.

Записывают результат сравнения с помощью знаков больше, меньше и знака равенство (&gt,, &lt,, =). Например, длина отрезка АБ — 2 см, а ВГ — 8 см, записываем результат сравнения так: АБ &lt, ВГ или ВГ &gt, АБ.

Это интересно: как разложить на множители квадратный трехчлен?

Сравнивать фигуры можно разными способами, выбор которых зависит от возможностей или условий:

• визуальный способ,
• измерительный,
• сравнение наложением,
• сравнение в координатной сетке.

Лучше всего, если они различаются по длине визуально, и, просто посмотрев на них, вы можете сказать, который длиннее. Но так бывает не всегда.

Измерение длины

Самый простой способ — измерение. Для этого можно использовать линейку, просто измерив длину отрезка, мы поймем, который из них длиннее. Если нет линейки, но они начерчены на листе в клетку, для измерения их длин можно посчитать клетки. В одном сантиметре две клетки. Это метод сравнения измерением длин, но есть еще метод сравнения наложением.

Обратите внимание: что такое луч в геометрии.

Наложение друг на друга

Как происходит совмещение АБ и ВГ:

• Нужно конец, А одного из них совместить с концом В другого, если совпадают и другие концы этих отрезков — Б и Г, значит, они равны, что записывается с помощью знака равно.
• Если нет, значит, один из них длиннее другого, и записывается это также с помощью математических знаков больше или меньше (&gt, или &lt,).

Бывает так, что при наложении одного отрезка на другой ровно половина одного из них будет совмещена с другим. Точку, которая делит его на две равные части, называют серединной точкой. И если у нас есть серединная точка В, то АВ=ВБ.

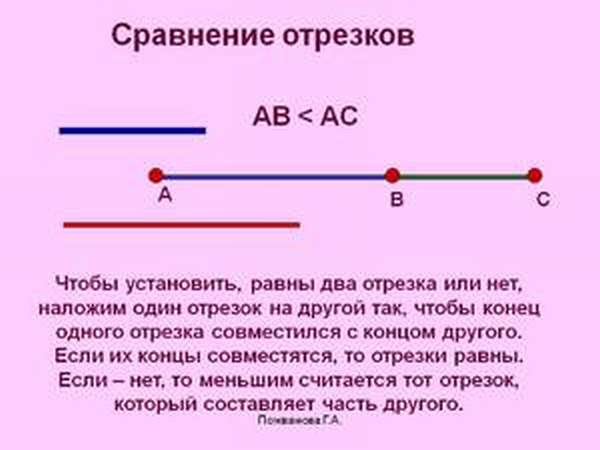
Примерно так же наложением сравнивают не только прямые, но и другие геометрические фигуры, а также углы.

Можно сделать «линейку» из полоски бумаги, при этом такую линейку не нужно линовать, достаточно отметить на ней начало и конец одного из отрезков. Затем вы прикладываете импровизированную линейку ко второму, совмещая его начало с первой отметкой и, сравниваете расположение второй отметки по отношению к его концу. Таким способом можно сравнивать и довольно большие фигуры, например, расстояние между столбиками забора, но использовать при этом лучше не бумажную полоску, а веревку.

Два отрезка называются равными, если их можно совместить методом наложения. Если есть возможность приложить их друг к другу, просто посмотрите, какой из них длиннее. Но так можно сделать не всегда.

Если под рукой имеется циркуль, поставьте одну ножку циркуля в начало, а другую в конец первого отрезка. Затем не сдвигая ножки циркуля, установите одну из них в начало второго и посмотрите, если вторая ножка циркуля в точке, обозначающей конец — они равны. Если вторая ножка на самой прямой — первый отрезок меньше, если за ним — первый больше.

Сравнение в координатной сетке

Допустим, что у нас есть два отрезка, координаты которых мы знаем — а (Х1, Y1, Х2, Y2) и b (Х3, Y3, X4, Y4).

Первое, что нужно сделать — придать координатам числовые значения:

• Длина, а — Da = √((X1 — X2) ² + (Y1 — Y2) ²),
• Длина b — Db = √((X3 — X4) ² + (Y3 — Y4) ²).

Пусть X1 = -7, Y1 = 4, X2 = 3, Y2 = -4, X3 = -3, Y3 = -5, X4 = 0, Y4 = -3. Получаем:

Da = √ ((-7 — 3) ² + (4 — (-4)) ²) = √ (-10 ² + 8 ²) = √ 100 + 64 = √ 164

Db = √ ((-3 — 0) ² + (-5 — (-3)) ²) = √ (-3 ² + (-8) ²) = √ (9+ 64) = √ 73

√ 164 &gt, √ 73, значит, Da &gt, Db.

Также можно сравнить отрезки, находящиеся в трехмерной системе координат, надо учитывать не две, а три координаты каждого из них.

Примеры

Рассмотрим сравнение методом наложения. У нас имеется два отрезка — АБ и ВГ.

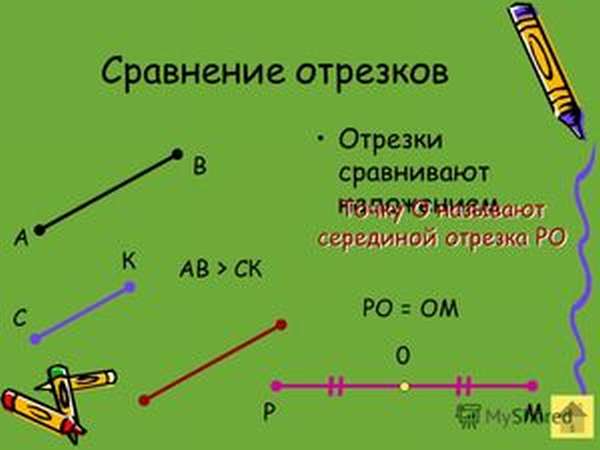
Чтобы узнать, равны они или нет, просто приложим их друг к другу так, чтобы их «начала» были в одной точке, то есть совместим точки, А и В.

Если мы видим, что АБ получается частью ВГ, значит, он меньше, то есть АБ&lt, ВГ, а если при наложении оба конца отрезков совмещаются — значит, они равны.

Теперь рассмотрим сравнение отрезков путем измерения. При помощи линейки вычисляем длину каждого отрезка. Например, длина AB = 2 см, а CD = 8 см. 8&gt,2, значит, CD&gt,AB, то есть отрезок CD длиннее AB.

Источник

Подготовка к ЕГЭ: задача 18 (отрезки)

Описание презентации по отдельным слайдам:

Теория Задания№18 на логические отрезки можно решать несколькими способами. В данной презентации рассматриваются два способа решения. Как правило, в данных задачах логическое выражение, для которого требуется найти длину отрезка, на котором это выражение истинно (или ложно), достаточно сложно для восприятия. Поэтому необходимо его упростить. Нужно ввести дополнительные обозначений для простых логических высказываний и за счёт этого получить логическую функцию традиционного вида. Первый способ решения: полученное выражение нужно упростить, используя законы преобразования логических выражений. Итоговое выражение нужно приравнять 1, если по условию оно должно быть истинным, или 0, если должно быть ложно.

Источники сайт К. Полякова http://kpolyakov.spb.ru Открытый банк заданий ФИПИ С.С. Крылов, Т.Е. Чуркина ЕГЭ-2018 – типовые экзаменационные варианты. Информатика и ИКТ. Москва. Национальное образование. 2017 В.Р. Лещинер. Информатика. ЕГЭ-2018. Типовые тестовые задания. Москва. Издательство «Экзамен». 2017 Самылкина Н.Н. и др. Подготовка к ЕГЭ-2018. Информатика. Москва. Эксмо. 2017

Теория Остается только рассмотреть простые высказывания, входящие в итоговое выражение, и выяснить, на каких отрезках они истинны (или ложны, в зависимости от условия задачи). Проанализировав эти отрезки, нужно найти итоговый (или несколько, в ответе может быть не один). При втором способе решения для полученного после ввода обозначений выражения строится таблица истинности (ТИ), в которой отражены значения всех логических переменных и логических операций на каждом числовом отрезке. В одном из столбцов будут стоять значения искомой переменной. В зависимости от условия, она либо равна 1, либо равна 0, либо может принимать любое значение, поскольку не будет влиять на конечное значение исходного выражения. Остается выбрать строки, соответствующие условию задачи (истинно или ложно должно быть исходное выражение) и выбрать числовые отрезки (отрезок).

Рассмотрим числовую ось с нашими отрезками P и Q. Разбор решения задач Рассмотрим отдельно все три отрезка. Отрезок 10‒18: выражение истинно, т.к. Р=1 (x ϵ P) Отрезок 31‒ 40: выражение истинно, т.к. Q=1 (x ϵ Q) Отрезок 18‒31: выражение будет истинным в случае ¬A = 1, или А=0. Это значит, что А не принадлежит отрезку 18‒31, значение А должно быть совпадающим либо с отрезком Р, либо с отрезком Q. Но поскольку в задании спрашивается наименьшая длина отрезка, то это будет отрезок (18-10)=8 Ответ: 8 Задание 1.

На числовой прямой даны два отрезка: P=[10; 18] и Q=[31; 40]. Укажите наименьшую возможную длину такого отрезка A, что формула Разбор решения задач тождественно истинна, то есть принимает значение 1 при любом значении переменной x. Решение. Введем обозначения: P: x ϵ P, Q: x ϵ Q, A: x ϵ A Перепишем условие задания: ¬P Q + ¬A или ¬P ( Q + ¬A) (поскольку импликация имеет самый низкий приоритет и будет выполнена последней) Раскрываем импликацию: P + Q + ¬A Это выражение должно быть равным 1 при любом значении А: P + Q + ¬A = 1 Задание 1.

На числовой прямой даны два отрезка: P=[-10, 0] и Q=[-3, 8]. Выберите из предложенных вариантов такой отрезок А, что логическое выражение Разбор решения задач будет тождественно истинным, то есть будет принимать значение 1 при любом значении переменной х. 1) [-8, -4] 2) [-7, -1] 3) [-2, 5] 4) [-15, 15] Решение. Введем обозначения: P: x ϵ P, Q: x ϵ Q, A: x ϵ A Перепишем условие задания: Раскрываем импликацию, затем используем формулу де Моргана: ¬ ( P · A ) + (Q · A ) или ¬ P + ¬A + Q · A ( (x ϵ P) Ʌ (x ϵ A) ) ( (x ϵ Q) Ʌ (x ϵ A) ) ( P Ʌ A ) ( Q Ʌ A) Задание 2.

Разбор решения задач Преобразуем выражение, используя следующий закон преобразования: a + ¬a·b = a + b ¬ P + (¬A + Q · A) = ¬ P + (¬A + Q) = ¬A + ¬ P + Q Задание 2. Поскольку это выражение должно быть тождественно истинным, т.е. равным 1 при любом значении А, то ¬A должно быть истинным там, где (¬ P + Q) ложно, или где истинно ¬ (¬ P + Q). Преобразуем получившееся выражение, используя формулу де Моргана: ¬ (¬ P + Q) = (¬ ¬ P ) Ʌ ¬Q = P Ʌ ¬Q

Рассмотрим числовую ось с нашими отрезками P и Q. Разбор решения задач Выражение (P Ʌ ¬Q) истинно на отрезке [-10, -3]. На нем должно быть ¬A=1 или А=0. Это означает, что отрезок А не должен содержать в себе отрезок [-10, -3]. Рассмотрим варианты ответов. Отрезок 1) [-8, -4] содержит в себе значения из отрезка [-10, -3], поэтому не является правильным ответом. Отрезок 2) [-7, -1] содержит в себе значения из отрезка [-10, -3], что быть не должно. Отрезок 4) [-15, 15] содержит в себе значения из отрезка [-10, -3], что быть не должно. Отрезок 3) [-2, 5] не содержит в себе значения [-10, -3], поэтому именно он и является ответом. Ответ: 3) Задание 2.

На числовой прямой даны два отрезка: R=[27; 50] и S=[30; 67]. Укажите наименьшую возможную длину такого отрезка T, что формула Разбор решения задач тождественно истинна, то есть принимает значение 1 при любом значении переменной x. Решение. Введем обозначения: R: x ϵ R, S: x ϵ S, T: x ϵ T Перепишем условие задания: R (( S Ʌ ¬T ) R) Задание 3. (x ϵ R) (((x ϵ S) Ʌ ¬(x ϵ T)) ¬(x ϵ R))

Разбор решения задач Задание 3. Преобразуем получившееся выражение, используя замену импликации и формулу де Моргана: R (¬ ( S Ʌ ¬ T) + ¬ R) R (¬ S + T + ¬ R) ¬ R + ¬ S + T + ¬ R ¬ R + ¬ S + T Это выражение должно быть равно 1 при любом значении T: T + ¬ R + ¬ S = 1

Рассмотрим числовую ось с нашими отрезками P и Q. Разбор решения задач Чтобы получившееся выражение было везде истинным, T должно быть истинным там, где ложно (¬R + ¬S), т.е. там, где истинно выражение ¬ (¬R + ¬S). Выполним преобразования, используя формулу де Моргана: ¬ (¬ R + ¬ S) = ¬ ¬ R Ʌ ¬ ¬ S) = R Ʌ S = 1 Это выражение истинно на отрезке [30; 50]. Его длина равна (50 – 30) = 20 Ответ: 20 Задание 3.

На числовой прямой даны два отрезка: P=[2, 10] и Q=[6, 14]. Выберите из предложенных вариантов такой отрезок А, что логическое выражение Разбор решения задач будет тождественно истинным, то есть будет принимать значение 1 при любом значении переменной x. 1) [0, 3] 2) [3, 11] 3) [11, 15] 4) [15, 17] Решение. Эту задачу решим с помощью анализа исходного логического выражения после его преобразования, а также с помощью таблицы истинности. Введем обозначения: P: x ϵ P, Q: x ϵ Q, A: x ϵ A Перепишем условие задания: A P V Q = ¬ A + P + Q Задание 4. ( ( x ϵ A) ( x ϵ P) V ( x ϵ Q) )

1 способ. Чтобы полученное выражение везде равнялось 1 , ¬A должно быть либо 14, поскольку в интервале [2, 14 ] имеем либо P=1 либо Q=1 . Значит, А принадлежит отрезку [2, 14]. Этот отрезок входит в интервал под номером 3). 2 способ. Разобьем числовую ось ключевыми точками на несколько областей и составим ТИ для логического выражения. Разбор решения задач По ТИ получаем значения ¬A 14. Тогда решением задания будет 2 14 0 0 0 1 1

На числовой прямой даны два отрезка: P=[2, 20] и Q=[15, 25]. Выберите из предложенных вариантов такой отрезок А, что логическое выражение Разбор решения задач будет тождественно истинным, то есть будет принимать значение 1 при любом значении переменной x. 1) [0, 15] 2) [10, 25] 3) [2, 10] 4) [15, 20] Решение. Эту задачу решим с помощью таблицы истинности. Введем обозначения: P: x ϵ P, Q: x ϵ Q, A: x ϵ A Перепишем условие задания: (¬A ¬P ) V Q = A + ¬ P + Q Задание 5. ( ( x ɇ A) ( x ɇ P) ) V ( x ϵ Q)

Разобьем числовую ось ключевыми точками на несколько областей и составим ТИ для логического выражения. Разбор решения задач Из ТИ получаем, что значения А=1 будут на интервале 2 25 0 1 1 1 любое 1

Задачи для самостоятельного решения Задание 6. На числовой прямой даны два отрезка: P=[10; 18] и Q=[31; 40]. Укажите наибольшую возможную длину такого отрезка A, что формула (x ϵ P) V ¬ ( x ϵ A) V ( x ϵ Q) тождественно истинна, то есть принимает значение 1 при любом значении переменной x. Ответ: 9

Задачи для самостоятельного решения Задание 7. На числовой прямой даны два отрезка: R=[10; 30] и S=[20; 40]. Укажите наибольшую возможную длину такого отрезка T, что формула тождественно истинна, то есть принимает значение 1 при любом значении переменной x. Ответ: 30 (x ϵ T) ((x ϵ R) V (x ϵ S))

Задачи для самостоятельного решения Задание 8. На числовой прямой даны два отрезка: R=[20; 50] и S=[30; 65]. Укажите наименьшую возможную длину такого отрезка T, что формула Ответ: 20 тождественно истинна, то есть принимает значение 1 при любом значении переменной x. ¬ (x ϵ T) ((x ϵ R) ¬ (x ϵ S))

Задачи для самостоятельного решения Задание 9. На числовой прямой даны два отрезка: P=[10; 25] и Q=[0; 12]. Выберите из предложенных вариантов такой отрезок А, что формула тождественно истинна, то есть принимает значение 1 при любом значении переменной x. 1) [10, 15] 2) [20, 35] 3) [5, 20] 4) [12, 40] Ответ: 4) ( ( x ɇ Q) ( x ɇ P) ) V ( x ϵ A)

Задачи для самостоятельного решения Задание 10. На числовой прямой даны два отрезка: P = [10, 40] и Q = [30, 50]. Отрезок A таков, что формула тождественно истинна, то есть принимает значение 1 при любом значении переменной х. Какова наибольшая возможная длина отрезка A? 1) 10 2) 20 3) 30 4) 40 Ответ: 2) (( x ϵ A) ( x ϵ Q)) V ( x ϵ P)

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 813 человек из 76 регионов

Курс профессиональной переподготовки

Математика и информатика: теория и методика преподавания в образовательной организации

• Сейчас обучается 598 человек из 76 регионов

Курс повышения квалификации

Современные педтехнологии в деятельности учителя

• Курс добавлен 23.09.2021
• Сейчас обучается 48 человек из 23 регионов

Ищем педагогов в команду «Инфоурок»

Номер материала: ДБ-1484441

Международная дистанционная олимпиада Осень 2021

Не нашли то что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Безлимитный доступ к занятиям с онлайн-репетиторами

Выгоднее, чем оплачивать каждое занятие отдельно

Минпросвещения будет стремиться к унификации школьных учебников в России

Время чтения: 1 минута

Рособрнадзор откажется от ОС Windows при проведении ЕГЭ до конца 2024 года

Время чтения: 1 минута

Минобрнауки разработало концепцию преподавания истории российского казачества

Время чтения: 1 минута

Минпросвещения разрабатывает образовательный минимум для подготовки педагогов

Время чтения: 2 минуты

Российские школьники завоевали пять медалей на олимпиаде по физике

Время чтения: 1 минута

В Северной Осетии организовали бесплатные онлайн-курсы по подготовке к ЕГЭ

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник