Различные способы решения арифметических задач
По альтернативным методикам предлагаются разнообразные способы решения задач, например:
1) решение задач способом подбора;
2) решение задач методом целенаправленного перебора;
3) решение комбинаторных задач. При их решении пользуются графом.
4) графический способ решения
5) практический способ.
Приведем пример решения одной задачи разными способами из статьи Романовой Т.Д. «Решение задач разными способами».
Задача № 1. («Математика» Моро М.И. 1-3 № 20 с. 147). Две бригады рабочих должны посадить 490 деревьев. Сколько деревьев посадит каждая бригада, если распределить эту работу по числу рабочих и если в первой бригаде 34 рабочих, а во второй 36 рабочих.
Составим краткую запись в виде таблицы:
| Производительность труда рабочего | Кол-во рабочих в бригаде | Объем выполненной работы | |
| I | одинаковая | 34 р. | ? > 490 д. ? |
| II | 36 р. |
По данной краткой записи может видеть три способа ее решения.
1 способ. 1)34+36=70(р.) — всего рабочих в двух бригадах
2)490:70=7(д.) — производительность труда рабочего
3)34*7=238(д.) — посадит первая бригада
4)36*7=252(д.) — посадит вторая бригада
2 способ . 1)34+36=70(р.) — всего рабочих в двух бригадах
2)490:70=7(д.) — производительность труда рабочего
3)34*7=238(д.) — посадит первая бригада
4)490-238=252(д.) — посадит вторая бригада
3 способ . 1)34+36=70(р.) — всего рабочих в двух бригадах
2)490:70=7(д.) — производительность труда рабочего
3)36*7=252(д.) — посадит вторая бригада
4)490-252=238(д.) — посадит первая бригада.
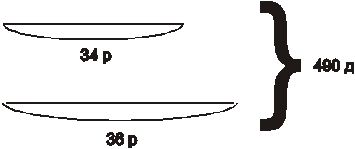 |
Воспользуемся графической иллюстрацией для составления краткой записи:
Предположим, что число рабочих в каждой бригаде одинаковое и каждая бригада посадила деревьев поровну. Этот прием — выдвижение гипотезы — позволяет изменить схему.
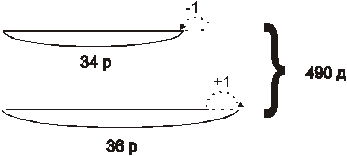 |
Рис.2
Данная схема побуждает к следующим способам решения задач:
4 способ . 1)34+36=70(р.) — всего рабочих в двух бригадах
2)70:2=35(р.) — в каждой бригаде по предположению
3)490:2=245(д.) — посадила бы каждая такая бригада
4)245:35=7(д.) — производительность труда рабочего
5)34*7=238(д.) — посадит первая бригада
6)36*7=252(д.) — посадит вторая бригада
5 и 6 способы основаны на предположении о равночисленности рабочих в бригадах и, следовательно, на одинаковом объеме выполненных работ. 5 и 6 способы имеют первые три действия аналогичные первым трем действиям способа 4, а последние действия аналогичны действиям 3 и 4 в способах 2 и 3.
7 способ. Предположим только, что обе бригады посадили деревьев поровну. Тогда 1)490:2=245(д.) — могла бы посадить каждая бригада
2)34+36=70(р.) — всего рабочих в двух бригадах
3)490:70=7(д.) — производительность труда рабочего
4)245-7=238(д.) — посадит первая бригада рабочих
5)245+7=252(д.) — посадит вторая бригада
8 способ. Воспользуемся четность чисел и предположим, что рабочие выполняют предложенный объем работы в парах. Тогда
1)34:2=17(п.) — число пар рабочих в первой бригаде
2)36:2=18(п.) — число пар рабочих во второй бригаде
3)17+18=35(п.) — всего пар в двух бригадах
4)490: 35=14(д.) — производительность труда пары рабочих
5)14*17=238(д.) — посадит первая бригада
6)14*18=252(д.) — посадит вторая бригада
9 и 10 способы также основаны на предположении о выполнении объема работ по посадке деревьев рабочими в парах. Данные способы имеют первые четыре действия аналогичные первым четырем действиям способа 8.Последующие 5 и 6 действия могут быть такими:
Например для способа 9: 14*17=238(д.) — посадит первая бригада
490-238=252(д.) — посадит вторая бригада .
Для 10 способа: 18*14=252(д.) — посадит вторая бригада
490-252=238(д.) — посадит первая бригада.
Внесем изменения в схему:
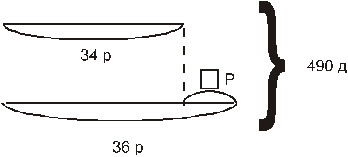 |
Рис.3
Воспользуемся разностью в численности рабочих бригад .
11 способ. 1)36-34=2(р.) — разница
2)36+34=70(р.) — всего рабочих
3)490:70=7(д.) — производительность труда одного рабочего
4)7*2=14(д.) — посадят деревьев два рабочих
5)34*7=238(д.) — посадит первая бригада
6)238+14=252(д.) — посадит вторая бригада
12 способ. Рассуждения аналогичны рассмотренным в способе 11, но в пятом действии узнаем, сколько посадит деревьев вторая бригада 36*7=252(д.), а уже после найдем, сколько посадит деревьев первая бригада.
Рассмотренные способы называют арифметическим. В заключении
можно выделить еще два способа — алгебраический и графический.
13 способ(алгебраический). Пусть х — число деревьев, посаженных одним рабочим. Тогда две бригады посадят (34+36)*х. Всего надо посадить 490 деревьев.
Составим уравнение: (34+36)*х=490
Решая уравнение, находим, сколько деревьев посадит один рабочий:
х=7. Отсюда:7*34=238(д.) — посадит первая бригада
7*36=252(д.) — посадит вторая бригада
 |
14 способ(графический)
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Источник
Следовательно , задачи выполняют мировоззренческую, дидактическую, развивающую, воспитывающую функции



Задача
ПЛАН
Арифметические задачи в НКМ
ОБЩИЕ ВОПРОСЫ МЕТОДИКИ ОБУЧЕНИЯ РЕШЕНИЮ АРИФМЕТИЧЕСКИХ ЗАДАЧ
1. Задача и её структура.
2. Способы решения арифметических задач.
3. Роль и место текстовых задач в НКМ.
4. Система задач, представленных в НКМ.
Литература дополнительная: ТОНКМ, § 4
1. Истомина Н. Б. МПМ в начальных классах, гл.4, № 4.1
2. Матвеева Н.А. Различные арифметические способы решения задач// НШ. — 2001. — № 3 (приёмы обучения поиску разных способов).
1. Задача и ее структура
Задача (в широком смысле) – это особая форма познания действительности. Задача – это требование найти некоторый результат, когда пути и действия по его нахождению явно не указываются, но в тексте задачи имеется для этого необходимая специфическая информация.
“ Проблема” (греч.)- “задача”, “задание”.
Где мы сталкиваемся с задачами?
“Арифметика” (греч) – “число.
Для класса арифметических задач характеристическим свойством является тот факт, что ответ на вопросы задачи может быть получен при помощи арифметических действий ( без привлечения каких – либо иных знаний ).
А Р И Ф М Е Т И Ч Е С К И Е З А Д А Ч И
 |
II —? на 4 меньше.
Что записано кратко: условие или задача? Закончите предложение:
“Прочитайте….” (условие или задач).
2.Способы решения арифметических задач
Решить арифметическую задачу – это значит:
1) установить связи между данными, между данными и искомым;
2) осуществить на этой основе выбор плана (в т. ч. и арифметического действия);
3) выполнить намеченный план (арифметическое действие);
4) дать ответ на вопрос задачи.
 |  |
У → Математическая → Выполнение → Ответ → Семантическая
В модель арифм. действий (число) трактовка

Т. о., решение задачи — это перевод сюжетного текста на математический язык и обратный перевод с языка математики на свой родной язык.
Трудно ли учить решать задачи?
Путь, который мы проходим от условия задачи (с ориентированием на её вопрос) к ответу на этот вопрос, т. е. решение задачи, непременно связано с мышлением, которое может осуществляться на различных уровнях и в различных формах. Недаром арифметические задачи называют мощным средством развития мышления.
| ведущий тип мышления | наглядно-образное, наглядно-схематическое | словесно-логическое, абстрактное |
| уровень познания | чувственное: ощущения, восприятие, представление | рациональное: понятия, суждения, умозаключения |
| виды моделей | предметы, их изобра – жение, условные заме- нители реальных объ- ектов | числа, переменные, отношения между ними |
| способы решения арифметических задач | практический, геомет- рический (графический) | арифметический, алгебраический |
От чего зависит выбор способа решения?
2. СПОСОБЫ РЕШЕНИЯ АРИФМЕТИЧЕСКИХ ЗАДАЧ
1. Практический: полная предметная наглядность, манипулирование
предметами (операции над множествами), ответ находится
2. Геометрический (графический): геометрическая модель действия (построения) на чертеже, ответ находится путём измерения или счёта.
3. Арифметический: частичная предметная наглядность или чертёж, полное отсутствие наглядности, ответ находится вычислением.
4.Алгебраический: составляется и решается уравнение, ответ нахо-дится путём вычислений.
5. Подбора (проб-универсальный, но, как правило, нерациональный
отсутствие модели; ответ находиться вычислением.
Геометрический (графический) способ близок к практическому, но использует наглядность более абстрактного характера. В начальном обучении преимущественно преобладают практический и арифметический способы решения арифметических задач. Причём обучение решению задач строится так, что постепенно и своевременно переходят от практического к арифметическому:

 |
в случае затруднений, для контроля понимания,

для обоснования правильности решения


наглядность наглядность наглядности
 |
в случае затруднений, для самоконтроля и
контроля, для проверки задачи
Т. о. каждую арифметическую задачу можно решить 4 – 5 разными способами. Способ решения определяется выбором модели для данной задачи, от чего существенно зависит способ нахождения ответа.
Два арифметических способа решения считаются разными, если они отличаются планом решения:
1) числом арифметических действий;
2) хотя бы одним действием;
Например: 1) (3 + 4) · 2= 14; Составьте задачу про книги
2) 3 · 2 + 4 · 2=14; на двух полках по выражению:
4 · 2 = 8; Среди указанных четырех способов
6 · 8 = 14; ее решения найдите разные и одинаковые.
3. Роль и место текстовых задач в НКМ
Нужны ли задачи в НКМ?
Обучение решению арифметических задач является неотъемлемой составной частью обучения математике. Учить математике – это значит учить думать, говорить, переводить самые разные реальные ситуации на математический язык, чтобы познавать реальность собственно математическими методами. Текстовые задачи выступают в роли заменителя, т. е. модели многообразия существующих в окружающем мире связей, закономерностей, отношений. В то же время обучение математике ведется через систему задач.
Роль арифметических задач: с одной стороны — подсобная, вспомогательная, а с другой — самостоятельная, т.е. задача одновременно является и средством обучения и содержанием обучения.
 |
Задача выступает в качестве средства:
— связи обучения с жизнью;
— наглядности при ознакомлении с понятиями, отношениями, законами;
— закрепления теоретических знаний;
— формирования вычислительных навыков;
4. Система задач, представленных в НКМ
Какие арифметические задачи включать в НКМ ?
Как их распределять?
Отбор арифметических задач и система их расположения в НКМ подчинены:
1) логике развёртывания вводимых в начальных классах математических знаний;
2) собственной логике ( от простых задач к составным ; от одного
типа к другому; сравнение задач разных типов и др.)
В методике принято классифицировать арифметические задачи не только на простые и составные, т. е. по количеству выполняемых при решении действий, но и по другим признакам.
Множество простых задач можно разбить на 4 класса по способу их решения, т.е. по арифметическому действию, которым можно найти ответ на вопрос задачи: на сложение, вычитание, умножение, деление.
Но составим, например, задачи по выражению 4 + 3.
— 
— Чем они отличаются?
(Разные теоретические основания для выбора арифметического действия, т.е. разные математические понятия (“ вместе”,“сумма”, “ на больше” в прямой и в косвенной форме, “ уменьшаемое”) или зависимости (как найти уменьшаемое).
Очевидно, что все эти теоретические знания младшие школьники приобретают не сразу в полном объёме, а постепенно, порционно. И каждая такая порция знаний моделируется с помощью текстовых задач.
Составьте теперь задачи с вопросом: “Сколько вместе?”
— 
— Какой из названных признаков является существенным с точки зрения математики? Обучения математике?
(Одинаковая зависимость между данными и искомым.)
По данному основанию можно провести классификацию не только множества всех простых арифметических задач, но и многих составных задач. Такую классификацию называют методической, потому что она имеет непосредственную практическую значимость для учителя – методика работы с задачами каждого класса имеет свою специфику, которую учителю нужно знать и учитывать в процессе обучения младших школьников.
По ОС № 7 назовите типы простых задач, собственных задач.
Современная технология обучения решению задач не предполагает заучивание и узнавание учащимися типов задач, т.к. это может привести к формализму знаний.
Источник













