Два арифметических способа решения задач считаются различными если они отличаются
СПОСОБЫ РЕШЕНИЯ ЗАДАЧ
Понятие “решение задачи” можно рассматривать с различных точек зрения: решение как результат, т.е. как ответ на вопрос, поставленный в задаче, и решение как процесс нахождения этого результата.
С точки зрения методики обучения решению задач на первый план выступает процесс нахождения результата, который в свою очередь, тоже можно рассматривать с различных точек зрения Во-первых, как способ нахождения результата и, во-вторых, как последовательность тех действий, который входят в тот или иной способ.
Восемь яблок разложили по 2 на несколько тарелок. Сколько понадобилось тарелок?
Учащиеся могут решить эту задачу, не имея никакого представления о делении и о записи этого действия, а только опираясь на свой жизненный опыт и владея счетом от 1 до 8. Для этого они отсчитывают 8 яблок, положат 2 на одну тарелку, затем 2 на другую и т.д. пока не разложат все. Посчитав количество тарелок, они ответят на поставленный вопрос. Такой способ и называется практическим или предметным. Его возможности ограничены, так как учащийся может выполнить предметные действия только с небольшим количеством предметов. Усвоив смысл действия деления и его запись, можно решить эту задачу уже не практическим, а арифметическим способом, записав равенство 8 : 2 = 4.
Для решения можно применить алгебраический способ, рассуждая при этом так: “Число тарелок неизвестно, обозначим их буквой Х. На каждой тарелке 2 яблока, значит число всех яблок — это 2х. Так как в условии известно, что число всех яблок 8, то можно записать уравнение 2х = 8 и решить его х = 8 : 2, х = 4”.
Задачи, в которых для ответа на вопрос нужно выполнить только одно действие, называются простыми. Если для ответа на вопрос задачи нужно выполнить два и более действий, то такие задачи называются составными. Составную задачу, так же как и простую можно решить, используя различные способы.
Рыбак поймал 10 рыб. Из них 3 леща, 4 окуня, остальные щуки. Сколько щук поймал рыбак?
Обозначим каждую рыбу кругом. Нарисуем 10 кругов и обозначим
пойманных рыб: л — лещи, о — окуни.
Для ответа на вопрос задачи можно не выполнять арифметические действия, так как количество пойманных щук соответствует тем кругам, которые не обозначены (их З).
1) 3 + 4 = 7 (р.) — пойманные рыбы
Для ответа на вопрос задачи мы выполнили два действия.
Пусть х — пойманные щуки
Тогда количество всех рыб можно записать выражением:
3 + 4 + х — все рыбы
По условию задачи известно, что рыбак поймал всего 10 рыб.
Значит 3 + 4 + х = 10
Решив это уравнение, мы ответим на вопрос задачи.
Этот способ, так же как и практический, позволяет ответить на вопрос задачи, не выполняя арифметических действий.
В начальных классах используются различные формы записи решения задач по действиям, по действиям с пояснением, с вопросами, выражением.
У мальчика было 90 книг. 28 он поставил на первую полку, 12 на вторую. Остальные на третью. Сколько книг на третьей пилке?
а) решение по действиям
Ответ: 50 книг на третьей полке.
б) по действиям с пояснением
1) 28 + 12 = 40 (к.) на 1 и 2 полках вместе.
2) 90 — 10 = 50 (к.) на 3 полке.
1) Сколько книг на первой и второй полках вместе?
2) Сколько книг на третьей полке?
При записи решения задачи выражением можно вычислить его значение. Тогда запись решения задачи будет выглядеть так:
90 — (28 + 12) = 50 (к.)
Не следует путать такие понятие как: решение задачи различными способами (практический, арифметический графический, алгебраический), различные формы записи арифметического способа, решения задачи (по действиям, выражением по действиям с пояснением, с вопросами) и решение задачи различными арифметическими способами. В последнем случае речь идет о возможности установления различных связей между данными и искомым, а, с следовательно, о выборе других действий или другой их последовательности для ответа на вопрос задачи.
Например, рассмотренную выше задачу можно решить другим арифметическим способом:
1) 90 — 28 = 62 (к.) на 2 и3 полках.
2) 62 — 12 = 50 (к.) на 3 полке.
В качестве арифметического способа можно рассматривать и такое решение данной задачи:
1) 90 — 12 = 78 (к.) на 2 и 3 полках.
2) 78 -28 = 50 (к.) на З полке.
В числе способов решения задач ложно назвать схематическое моделирование. В отличие от графического способа, который позволяет ответить на вопрос задачи, используя счет и присчитывание схема моделирует только связи и отношения между данными и искомыми. Эти отношения не всегда возможно, а порой даже нецелесообразно представлять в виде символической модели (выражение, равенство) Тем не менее моделирование текста задачи в виде схемы иногда позволяет ответить не вопрос задачи.
Когда из гаража выехало 18 машин, в нем осталось в 3 раза меньше, чем было. Сколько машин было в гараже?
Решение этой задачи арифметическим способом довольно сложно для ребенка. Но если использовать схему, то от нее легко перейти к записи арифметического действия. В этом случае запись решения будет иметь вид:
Ответ: 27 машин было в гараже
В альбоме для раскрашивания 48 листов. Часть альбома Коля раскрасил. Сколько листов осталось не раскрашенными, если Коля раскрасил в 2 раза больше, чем ему осталось?
Решение задачи можно оформить так:
48 : 3 = 16 (л.) Ответ: 16 листов
[../../../_private/navbar1.htm]
Источник
Следовательно , задачи выполняют мировоззренческую, дидактическую, развивающую, воспитывающую функции



Задача
ПЛАН
Арифметические задачи в НКМ
ОБЩИЕ ВОПРОСЫ МЕТОДИКИ ОБУЧЕНИЯ РЕШЕНИЮ АРИФМЕТИЧЕСКИХ ЗАДАЧ
1. Задача и её структура.
2. Способы решения арифметических задач.
3. Роль и место текстовых задач в НКМ.
4. Система задач, представленных в НКМ.
Литература дополнительная: ТОНКМ, § 4
1. Истомина Н. Б. МПМ в начальных классах, гл.4, № 4.1
2. Матвеева Н.А. Различные арифметические способы решения задач// НШ. — 2001. — № 3 (приёмы обучения поиску разных способов).
1. Задача и ее структура
Задача (в широком смысле) – это особая форма познания действительности. Задача – это требование найти некоторый результат, когда пути и действия по его нахождению явно не указываются, но в тексте задачи имеется для этого необходимая специфическая информация.
“ Проблема” (греч.)- “задача”, “задание”.
Где мы сталкиваемся с задачами?
“Арифметика” (греч) – “число.
Для класса арифметических задач характеристическим свойством является тот факт, что ответ на вопросы задачи может быть получен при помощи арифметических действий ( без привлечения каких – либо иных знаний ).
А Р И Ф М Е Т И Ч Е С К И Е З А Д А Ч И
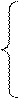 |
II —? на 4 меньше.
Что записано кратко: условие или задача? Закончите предложение:
“Прочитайте….” (условие или задач).
2.Способы решения арифметических задач
Решить арифметическую задачу – это значит:
1) установить связи между данными, между данными и искомым;
2) осуществить на этой основе выбор плана (в т. ч. и арифметического действия);
3) выполнить намеченный план (арифметическое действие);
4) дать ответ на вопрос задачи.
 |  |
У → Математическая → Выполнение → Ответ → Семантическая
В модель арифм. действий (число) трактовка

Т. о., решение задачи — это перевод сюжетного текста на математический язык и обратный перевод с языка математики на свой родной язык.
Трудно ли учить решать задачи?
Путь, который мы проходим от условия задачи (с ориентированием на её вопрос) к ответу на этот вопрос, т. е. решение задачи, непременно связано с мышлением, которое может осуществляться на различных уровнях и в различных формах. Недаром арифметические задачи называют мощным средством развития мышления.
| ведущий тип мышления | наглядно-образное, наглядно-схематическое | словесно-логическое, абстрактное |
| уровень познания | чувственное: ощущения, восприятие, представление | рациональное: понятия, суждения, умозаключения |
| виды моделей | предметы, их изобра – жение, условные заме- нители реальных объ- ектов | числа, переменные, отношения между ними |
| способы решения арифметических задач | практический, геомет- рический (графический) | арифметический, алгебраический |
От чего зависит выбор способа решения?
2. СПОСОБЫ РЕШЕНИЯ АРИФМЕТИЧЕСКИХ ЗАДАЧ
1. Практический: полная предметная наглядность, манипулирование
предметами (операции над множествами), ответ находится
2. Геометрический (графический): геометрическая модель действия (построения) на чертеже, ответ находится путём измерения или счёта.
3. Арифметический: частичная предметная наглядность или чертёж, полное отсутствие наглядности, ответ находится вычислением.
4.Алгебраический: составляется и решается уравнение, ответ нахо-дится путём вычислений.
5. Подбора (проб-универсальный, но, как правило, нерациональный
отсутствие модели; ответ находиться вычислением.
Геометрический (графический) способ близок к практическому, но использует наглядность более абстрактного характера. В начальном обучении преимущественно преобладают практический и арифметический способы решения арифметических задач. Причём обучение решению задач строится так, что постепенно и своевременно переходят от практического к арифметическому:

 |
в случае затруднений, для контроля понимания,

для обоснования правильности решения


наглядность наглядность наглядности
 |
в случае затруднений, для самоконтроля и
контроля, для проверки задачи
Т. о. каждую арифметическую задачу можно решить 4 – 5 разными способами. Способ решения определяется выбором модели для данной задачи, от чего существенно зависит способ нахождения ответа.
Два арифметических способа решения считаются разными, если они отличаются планом решения:
1) числом арифметических действий;
2) хотя бы одним действием;
Например: 1) (3 + 4) · 2= 14; Составьте задачу про книги
2) 3 · 2 + 4 · 2=14; на двух полках по выражению:
4 · 2 = 8; Среди указанных четырех способов
6 · 8 = 14; ее решения найдите разные и одинаковые.
3. Роль и место текстовых задач в НКМ
Нужны ли задачи в НКМ?
Обучение решению арифметических задач является неотъемлемой составной частью обучения математике. Учить математике – это значит учить думать, говорить, переводить самые разные реальные ситуации на математический язык, чтобы познавать реальность собственно математическими методами. Текстовые задачи выступают в роли заменителя, т. е. модели многообразия существующих в окружающем мире связей, закономерностей, отношений. В то же время обучение математике ведется через систему задач.
Роль арифметических задач: с одной стороны — подсобная, вспомогательная, а с другой — самостоятельная, т.е. задача одновременно является и средством обучения и содержанием обучения.
 |
Задача выступает в качестве средства:
— связи обучения с жизнью;
— наглядности при ознакомлении с понятиями, отношениями, законами;
— закрепления теоретических знаний;
— формирования вычислительных навыков;
4. Система задач, представленных в НКМ
Какие арифметические задачи включать в НКМ ?
Как их распределять?
Отбор арифметических задач и система их расположения в НКМ подчинены:
1) логике развёртывания вводимых в начальных классах математических знаний;
2) собственной логике ( от простых задач к составным ; от одного
типа к другому; сравнение задач разных типов и др.)
В методике принято классифицировать арифметические задачи не только на простые и составные, т. е. по количеству выполняемых при решении действий, но и по другим признакам.
Множество простых задач можно разбить на 4 класса по способу их решения, т.е. по арифметическому действию, которым можно найти ответ на вопрос задачи: на сложение, вычитание, умножение, деление.
Но составим, например, задачи по выражению 4 + 3.
— 
— Чем они отличаются?
(Разные теоретические основания для выбора арифметического действия, т.е. разные математические понятия (“ вместе”,“сумма”, “ на больше” в прямой и в косвенной форме, “ уменьшаемое”) или зависимости (как найти уменьшаемое).
Очевидно, что все эти теоретические знания младшие школьники приобретают не сразу в полном объёме, а постепенно, порционно. И каждая такая порция знаний моделируется с помощью текстовых задач.
Составьте теперь задачи с вопросом: “Сколько вместе?”
— 
— Какой из названных признаков является существенным с точки зрения математики? Обучения математике?
(Одинаковая зависимость между данными и искомым.)
По данному основанию можно провести классификацию не только множества всех простых арифметических задач, но и многих составных задач. Такую классификацию называют методической, потому что она имеет непосредственную практическую значимость для учителя – методика работы с задачами каждого класса имеет свою специфику, которую учителю нужно знать и учитывать в процессе обучения младших школьников.
По ОС № 7 назовите типы простых задач, собственных задач.
Современная технология обучения решению задач не предполагает заучивание и узнавание учащимися типов задач, т.к. это может привести к формализму знаний.
Источник