Как умножают японцы
Наши дети и мы привыкли умножать числа традиционным способом, записывая числа-множители столбиком.
Однако, в Азии детей учат совершенно другому приему умножения.
Умножая «в столбик», ребенку приходится держать в голове большие объемы данных. Японское умножение полезно показать всем детям, особенно любят данный способ визуалы и кинестеты. Ведь они могут увидеть умножение!
В этом видео мы рассказываем, как умножать по-японски:
Данный метод позволяет ребенку визуализировать умножение и решать примеры в рамках таблицы умножения и за ее пределами.
Например нам нужно умножить 12 на 12.
Шаг 1 — Горизонтально рисуем линии первого числа. Для каждого числа рисуется свое количество линий. Десятки и единицы разделяются промежутками. Например, для числа 12 единица рисуется одной линией. Двойка – чуть ниже двумя параллельными линиями. Для числа 36, 3 рисуется тремя линиями, 6 шестью параллельными линиями ниже и т.д.
Шаг 2 По аналогии с шагом 1, вертикальными линиями рисуем второе число 12:
Единицу – одной линией
Двойку – чуть отступив вправо двумя линиями
Шаг 3 Ставим на пересечениях линий точки
Шаг 4 Подсчитываем количество точек в трех группах, разделив их на «Рыбу»: хвост, голову и тело
Левый верхний угол – 1 (сотни)
Правый верхний и левый нижний углы (Диагональ) – 4 (десятки)
Правый нижний угол – 4 (единицы)
Шаг 5 Записываем результат: 144. Если у единиц или десятков получилось двухзначное число, то первая цифра добавляется к следующему разряду.
С помощью умножения «по-японски» дети могут легко посчитать любой пример таблицы умножения. Что нельзя сделать при традиционном подходе.
Забыв, ребенок легко может умножить 6 на 4 или 7 на 8.
Ему надо лишь нарисовать умножение!
Используйте этот прием и метод. И если ребенок на контрольной от волнения забудет таблицу умножения, он сможет на черновике посчитать «по-японски»!
В прошлое воскресенье, на занятиях в Школе спецагентов, детям очень понравился данный метод. Порисовав умножение, ребята применили еще два приема, которые позволили выучить таблицу умножения раз и навсегда.
В мире есть огромное количество уникальных техник, упрощающих жизнь и помогающих полюбить учиться.
Мы собрали их все, совместили со знанием детской психологией, добавили индвидуальный подход и обучаем детей лучшим мировым техникам обучения.
Давайте сделаем Вашим детям новогодний подарок — научим их учиться С удовольствием. Потому что учиться может быть очень увлекательно
Можно радоваться тому:
- Как здорово ты справился со всеми сложными словами и пишешь грамотно
- Как легко поддаются задачи по математике
- Как с помощью техники «Гамбургер» увлекательно пересказывать тексты
- Можно радоваться выученной таблице умножения, падежам, правилам русского и математике
- Можно побеждать сложных боссов, таких как физика или история
- И все это, спецагентскими приемами, необычными и увлекательнымиВ пакете стандрат дети научатся легко справляешься с самыми сложными заданиями по окружающему миру, математике, по русскому языку и красиво отвечать у доски.
- В пакете ПРО ребята изучат как эффективно учить и понимать английский, физику, историю, информатику.
- Научатся писать сочинения и изложения.
Мы используем собственную авторскую методику обучения.
Наши ученики не зубрят правила, они учатся думать, быть внимательными, верить в себя и не бояться трудностей, пишут грамотно и быстро и правильно считают.
Вам понравилась статья? Сохраните себе на стену, чтобы не потерять
Источник
Умножение по-японски, или как легко и быстро перемножить числа без калькулятора
Как умножают в японии: Учимся считать с помощью линий.
В век смартфонов-калькуляторов и голосовых помощников умножение больших чисел вручную уже кажется необычным и совершенно ненужным навыком. Но жизнь – непредсказуемая штука: никогда не знаешь, когда понадобится быстро что-то посчитать. И в этом деле идеальным помощником будет японский метод умножения (иногда его называют умножением по строкам). Все, что вам понадобится, – лист бумаги и ручка. Чтобы облегчить задачу, вы можете использовать чернила разных цветов, но это вовсе необязательно.
Давайте рассмотрим, как работает этот метод.
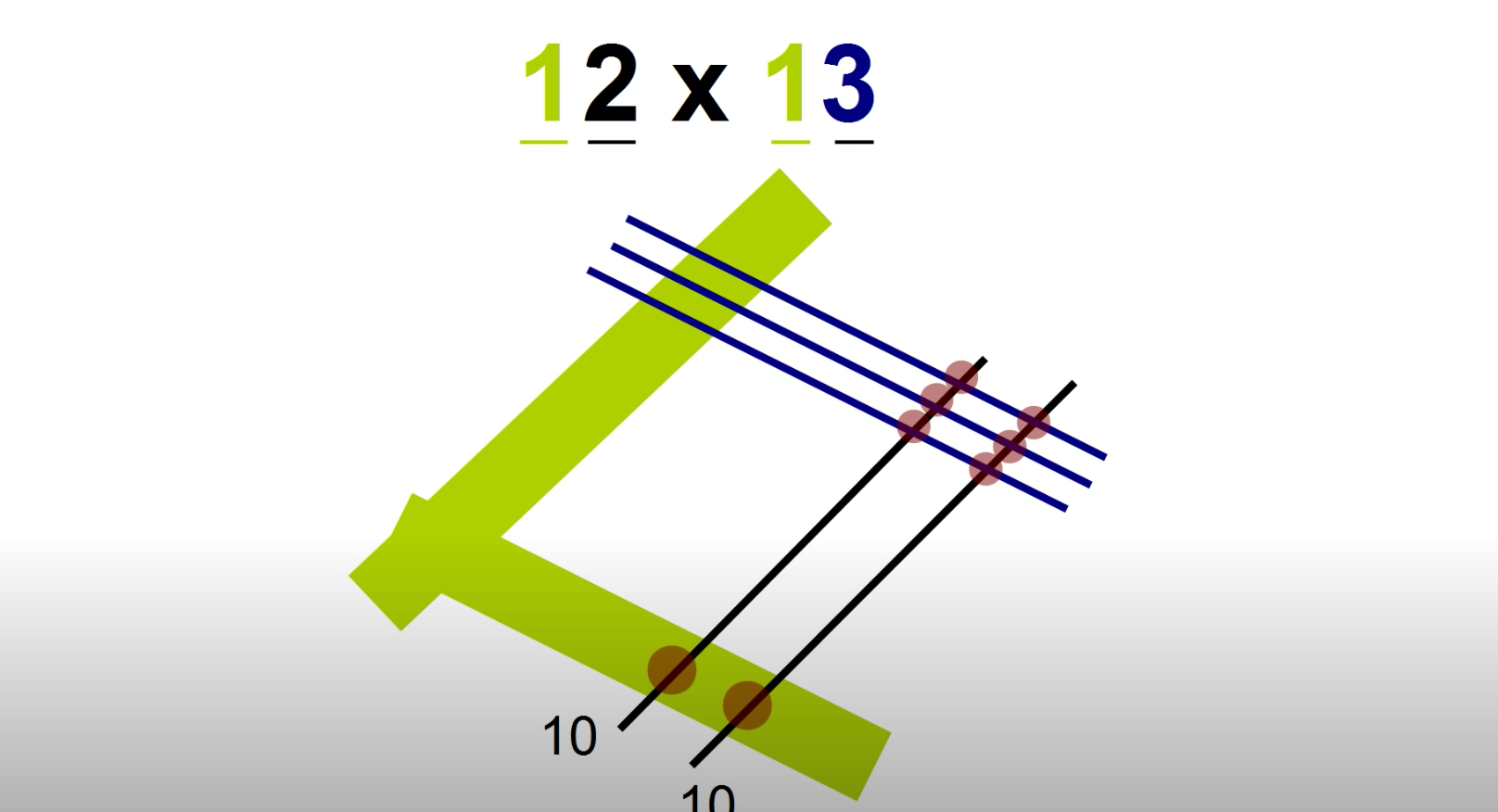
Посчитаем, сколько будет 12 x 13.
Первый шаг – рисуем линии. Один набор линий – для каждой «десятки» и параллельный набор – для разряда «единиц». У вас получится «квадрат», образованный одной линией для «десятков» числа 12 (зеленый цвет) + одной линией для «десятков» числа 13 (зеленый цвет) + двумя линиями для разряда «единиц» числа 12 (черный цвет) + тремя линиями для разряда «единиц» числа 13 (синий цвет). «Десятки» должны всегда располагаться слева, а прямоугольник – быть повернутым на 45 градусов.
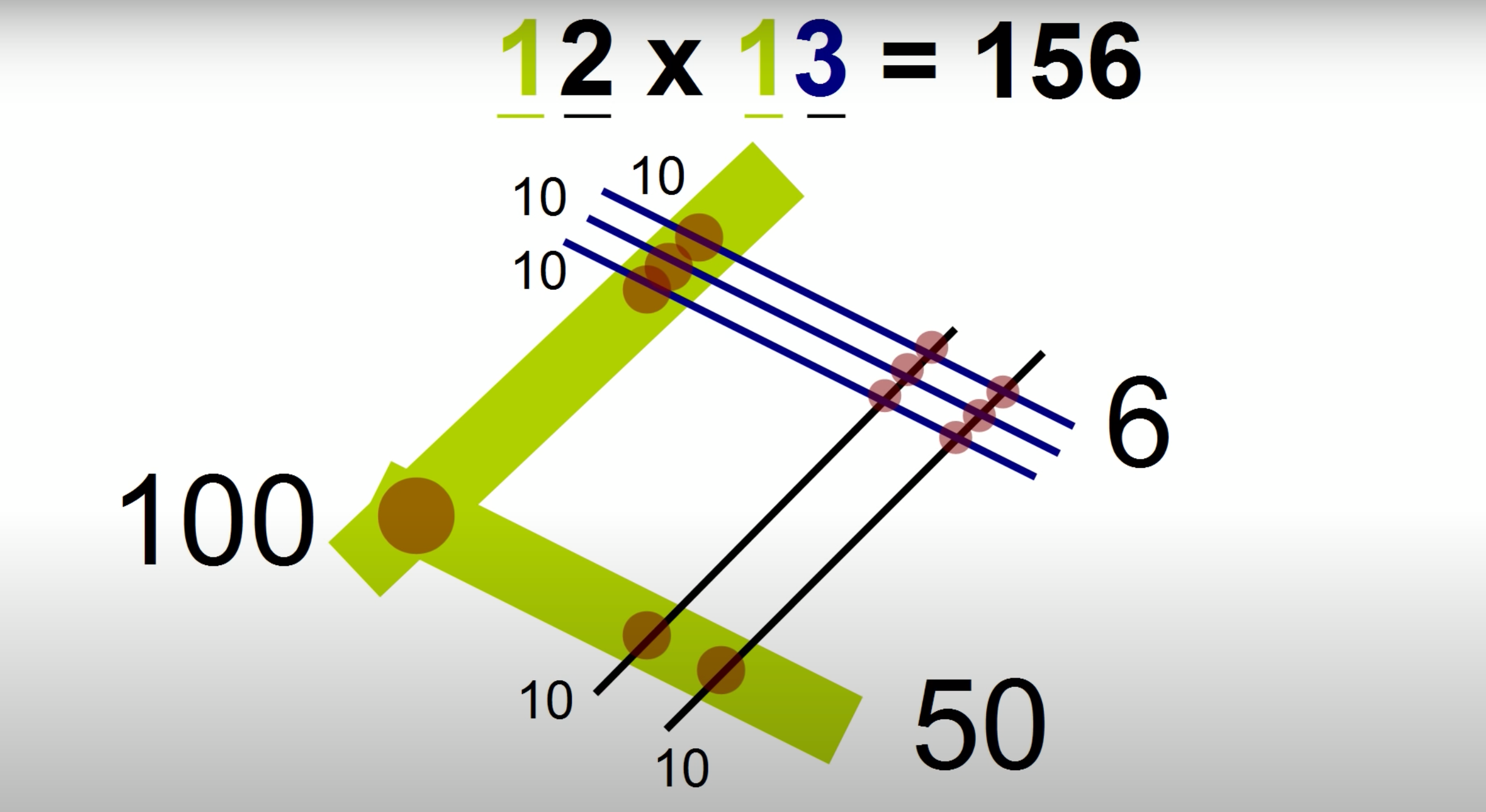
После того как вы нанесете на лист все линии, вам останется лишь нарисовать точки в местах пересечения и их подсчитать. В правом углу квадрата получится 6 точек (пересечения двух черных и трех синих линий). Эта цифра будет означать «единицы» в полученном числе, то есть стоять на последнем месте.
В нижнем углу видим 2 точки (пересечения разряда «десятков» числа 13 и двух черных линий). В верхнем углу – 3 точки (пересечение разряда «десятков» числа 12 и трех синих линий). Теперь сложим их вместе. Полученный результат 5 будет представлять разряд «десятков» в итоговом числе.
Наконец, в левом углу получилась 1 точка. В итоговом числе цифра 1 будет представлять разряд «сотен».
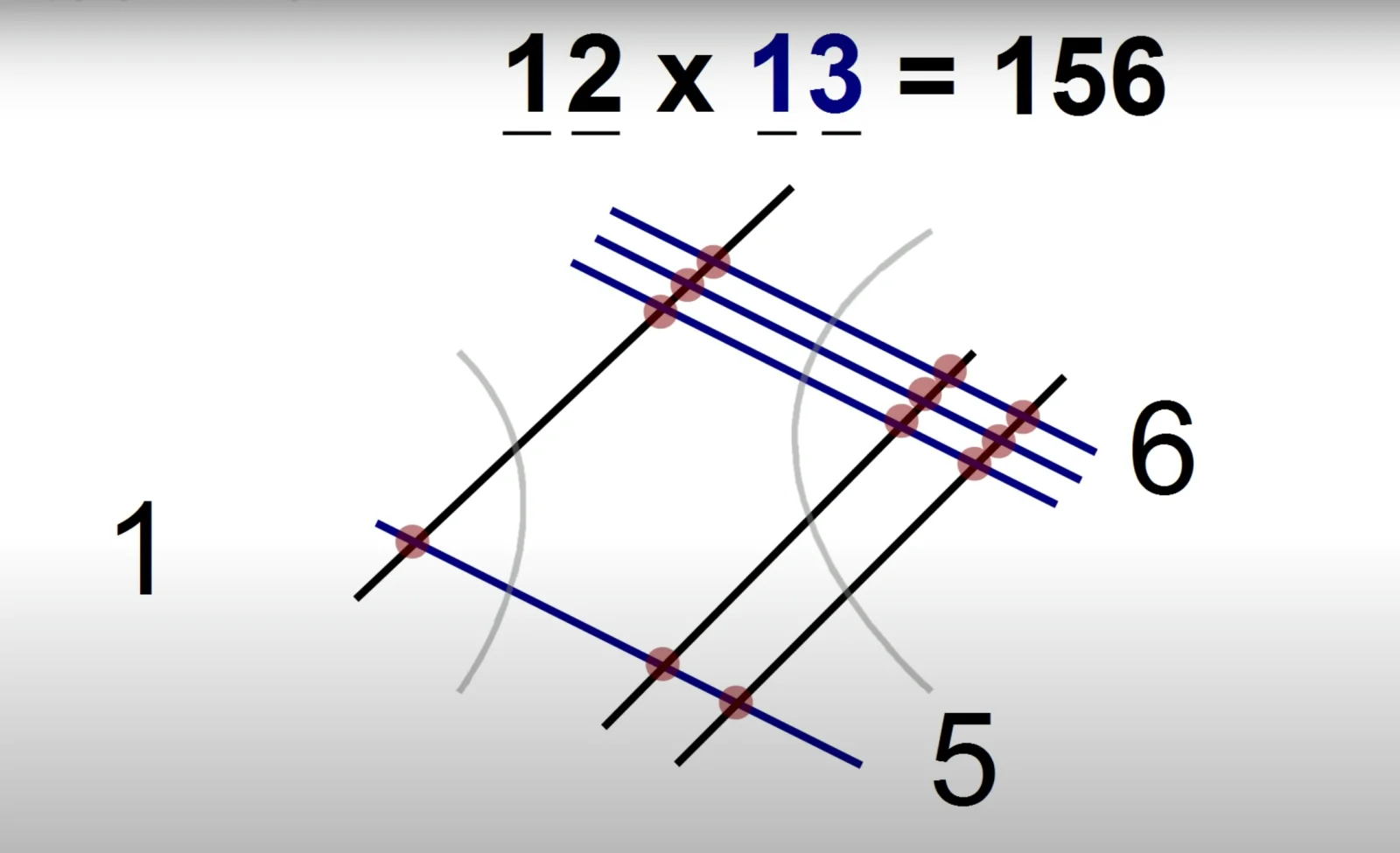
Возможно, вам будет удобнее отделять разряды на квадрате изогнутыми вертикальными линиями (как показано на рисунке). В любом случае, поставив каждую цифру на свое место, вы получите: 12 x 13 = 156 .
Этот метод работает и с гораздо большими числами. Просто попробуйте!
Вот видеопример как можно посчитать: 31х32, 213 x 13 и 103х23
Источник
Умножение: по-японски, по-итальянски и методом майя
Автор фото, Getty Images
Не заболела бы голова.
«Математика такая трудная. » Вы наверняка не раз слышали эту фразу, а, может быть, даже сами ее произносили вслух.
Для многих математические вычисления — дело непростое, но вот вам три несложных способа, которые помогут выполнить хотя бы одно арифметическое действие — умножение. Без калькулятора.
Вполне вероятно, что в школе вы познакомились с наиболее традиционным способом умножения: сначала вы выучили на память таблицу умножения, а уж затем стали в столбик перемножать каждую из цифр, которыми записываются многозначные числа.
Если вам надо перемножить многозначные числа, то, чтобы найти ответ, потребуется большой лист бумаги.
Но если от этого длинного набора идущих одна под другой строчек с цифрами у вас голова идет кругом, то есть и другие, более наглядные методы, которые могут вам помочь в этом деле.
Но тут пригодятся некоторые художественные навыки.
Давайте порисуем!
Как минимум три способа умножения связаны с рисованием пересекающихся линий.
1. Способ индейцев майя, или японский метод
Относительно происхождения этого способа существует несколько версий.
Трудно умножать в уме? Попробуйте метод майя и японцев
Мы быстро, просто и понятно объясняем, что случилось, почему это важно и что будет дальше.
Конец истории Подкаст
Некоторые говорят, что его придумали индейцы цивилизации майя, населявшие районы Центральной Америки до прибытия туда конкистадоров в XVI веке. Он также известен как японский метод умножения, поскольку учителя в Японии используют именно этот визуальный способ, когда учат младших школьников умножению.
Суть в том, что параллельные и перпендикулярные линии представляют цифры тех чисел, которые нужно перемножить.
Давайте умножим 23 на 41.
Для этого нам надо нарисовать две параллельные линии, представляющие 2, и, немного отступя, еще три линии, представляющие 3.
Затем, перпендикулярно к этим линиям мы нарисуем четыре параллельные линии, представляющие 4 и, чуть отступя, еще одну линию для 1.
Теперь нам надо пересчитать все точки пересечения этих линий. Именно так мы и получаем наш результат — 943, как если бы мы умножали в столбик.
Ну как, неужели трудно?
2. Индийский способ, или итальянское умножение «решеткой» — «джелозия»
Происхождение этого способа умножения тоже не ясно, однако он хорошо известен по всей Азии.
«Алгоритм «джелозия» передавался из Индии в Китай, затем в Аравию, а оттуда в Италию в XIV-XV веках, где он получил название «джелозия», поскольку внешне был похож на венецианские решетчатые ставни», — пишет Марио Роберто Каналес Виллануэва в своей книге, посвященной различным способам умножения.
Автор фото, Getty Images
Индийская или итальянская система умножения похожа на венецианские жалюзи
Давайте снова возьмем пример с умножением 23 на 41.
Теперь нам потребуется начертить таблицу из четырех клеток — по клетке на цифру. Подпишем сверху у каждой клетки соответствующую цифру — 2,3,4,1.
Затем надо разделить каждую клетку надвое по диагонали, чтобы получились треугольники.
Теперь мы сначала умножим первые цифры каждого числа, то есть 2 на 4, и запишем в первом треугольнике 0, а во втором 8.
Потом перемножим 3×4 и запишем 1 в первом треугольнике, а 2 во втором.
Проделаем то же самое и с другими двумя цифрами.
Когда все клетки нашей таблицы будут заполнены, мы складываем цифры в такой последовательности, как показано на видео, и записываем получившийся результат.
Трудно умножать в уме? Попробуйте индийский метод
Первая цифра у нас будет 0, вторая 9, третья 4, четвертая 3. Таким образом, результат получился: 943.
Как вам показалось, проще этот способ или нет?
Давайте попробуем еще один метод умножения с помощью рисунка.
Как и в предыдущем случае, для этого потребуется нарисовать таблицу.
Возьмем тот же пример: 23 x 41.
Тут нам надо разделить наши числа на десятки и единицы, поэтому 23 мы запишем как 20 в одной колонке, и 3 в другой.
По вертикали мы запишем наверху 40, а внизу 1 .
Затем мы перемножим числа по горизонтали и вертикали.
Трудно умножать в уме? Нарисуйте таблицу.
Но вместо того чтобы умножать 20 на 40, мы отбросим нули и просто перемножим 2 x 4, получив 8.
То же самое сделаем, умножая 3 на 40. Мы удерживаем в скобках 0 и умножаем 3 на 4 и получаем 12.
Проделаем то же самое с нижним рядом.
Теперь добавим нули: в левой верхней клетке у нас получилось 8, но мы отбросили два нуля — теперь мы их допишем и получится 800.
В правой верхней клетке, когда мы умножали 3 на 4(0), у нас получилось 12; теперь мы допишем ноль и получим 120.
Сделаем так же со всеми прочими удержанными нулями.
И наконец, мы складываем все четыре числа, полученных умножением в таблице.
Результат? 943. Ну как, помогло?
Важно разнообразие
Автор фото, Getty Images
Все способы хороши, главное — чтобы ответ сошелся
Что точно можно утверждать, — так это то, что все эти разные способы дали нам один и тот же результат!
Нам все-таки пришлось кое-что перемножить в процессе, но каждый шаг был проще, чем при умножении традиционным способом, и гораздо более наглядный.
Так почему же мало где в мире в обычных школах учат этим методам вычисления?
Одной из причин может быть упор на обучение «вычислениям в уме» — чтобы развивать умственные способности.
Однако Дэвид Уиз, учитель математики из Канады, работающий в государственных школах в Нью-Йорке, объясняет это иначе.
«Недавно я прочитал, что причина, по которой используется традиционный метод умножения, — это экономия бумаги и чернил. Этот метод не был придуман как самый простой для использования, но как самый экономный с точки зрения ресурсов, поскольку чернила и бумага были в дефиците», — объясняет Уиз.
Автор фото, Getty Images
Для некоторых методов вычисления только головы недостаточно, нужны еще и фломастеры
Невзирая на это, он полагает, что альтернативные методы умножения очень полезны.
«Я не думаю, что это полезно — сразу учить школьников умножению, заставляя их выучивать таблицу умножения, но не объясняя им при этом, откуда она взялась. Поскольку если они забудут одно число, то как они смогут продвинуться в решении задачи? Метод майя или японский метод необходим, потому что с его помощью вы можете понять общую структуру умножения, а это хорошее начало», — полагает Уиз.
Существует и ряд других способов умножения, например, русский или египетский, они не требуют дополнительных навыков рисования.
Как говорят специалисты, с которыми мы беседовали, все эти методы помогают лучше понять процесс умножения.
«Понятно, что все идет на пользу. Математика в сегодняшнем мире открыта как внутри, так и снаружи классной комнаты», — резюмирует Андреа Васкес, учительница математики из Аргентины.
Источник
Древний японский способ умножения
Японские методы умножения
Автор работы награжден дипломом победителя II степени
Всем в жизни приходится производить различные вычисления, в том числе и умножать двузначные числа. В школе нас учат умножать числа «в столбик». В интернете случайно увидел видео, в котором показывают интересный и быстрый метод умножения. Начал изучать этот метод, оказалось, что этот метод называется японский. Единственный ли это способ умножения чисел и всегда и во всех ли странах так умножают? Может быть, есть способы умножения проще, чем изучаемый в школе способ умножения чисел «в столбик»? Таким образом, перед нами поставлена цель исследования — изучить японский метод умножения и изготовить прибор для умножения двухзначных чисел.
Объект исследования — умножение двухзначных чисел.
Предмет исследования – японский метод умножения чисел.
Провести поиск разных способов умножения чисел в литературных источниках.
Овладеть различными способами умножения.
Разобраться в японском методе умножения.
Изготовить прибор для умножения, используя японский метод умножения двухзначных чисел.
Продуктом исследования является прибор для умножения двухзначных чисел.
Глава 1. Теоретическая часть
В начале развития общества , когда человеку не требовались большие числа, люди для счета обходились пальцами одной руки, потом двух, потом пальцами рук и ног. Позже все чаще возникала необходимость пересчитывать такое количество предметов, на которое пальцев не хватало. Постепенно были придуманы новые приема счета. В Африке некоторые племена до сих пор считают на камешках и орехах. Доходя до 5, складывают их отдельно в маленькую кучку. Жители островов Тихого океана ведут счет на кокосовых черешках , откладывая маленький черешок каждый раз, как они доходят до 10, и большой, – когда доходят до 100. Прошли многие тысячи лет. Развились обмен и торговля, которые потребовали от людей новых навыков в счете, в действиях с числами. [1]
Умножение — это особый случай сложения нескольких одинаковых чисел. В далекие времена люди учились умножать уже при счете предметов. Так, считая по порядку числа 17, 18, 19, 20, они должны были представлять 20 не только как 10+10, но и как два десятка, то есть 2 • 10; 30 — как три десятка, то есть три раза повторить слагаемым десяток — 3 · 10 — и так далее. [2]
Умножать люди начали значительно позже, чем складывать. Египтяне выполняли умножение посредством повторного сложения или последовательного удвоения. В Вавилоне при умножении чисел пользовались специальными таблицами умножения — «предками» современных. В Древней Индии применяли способ умножения чисел , тоже довольно близкий к современному. Индийцы производили умножение чисел начиная с высших разрядов. При этом они стирали те цифры, которые при последующих действиях надо было заменять, так как к ним прибавляли число, ныне запоминаемое нами при умножении. Таким образом, математики Индии сразу записывали произведение , выполняя промежуточные вычисления на песке или в уме. Индийский прием умножения перешел к арабам. Но арабы не стирали цифры, а перечеркивали их и надписывали новую цифру над перечеркнутой. В Европе продолжительное время произведение называли сумма умножения. Название «множитель» упоминается в работах VI веке, а «множимое» — в XIII веке. В XVII веке некоторые из математиков стали обозначать умножение косым крестиком — х, а иные употребляли для этого точку ( · ). В XVI — XVII веках для обозначения действий применяли различные символы — единообразия в их употреблении не было. Только в конце XVIII веке большинство математиков стали употреблять в качестве знака умножения точку, но допускали и употребление косого креста. Знаки умножения (•, х) и знак равенства (=) стали общепризнанными благодаря авторитету знаменитого немецкого математика Готфрида Вильгельма Лейбница (1646— 1716). [1]
Таблицу умножения (Приложение А, рис. 1) принято называть таблицей Пифагора, однако, автором ее был вовсе не древнегреческий математик. По крайней мере, этому нет никаких подтверждений. Тогда как факты, подтверждающие обратное – есть.
Археологи не один раз находили деревянные дощечки с фрагментами записей, подтверждающих, что подсчет при помощи таблицы вели уже в древней Японии и Китае. На раскопках на месте японского города Нара нашли табличку, относящуюся к VIII веку. [1]
До этого в окрестностях Киото, там, где когда-то находилась еще одна японская столица, Хэйнан, были обнаружены более поздние таблицы, датированные X-XI веками. Но интереснее всего то, что найденная в Нара табличка исписана иероглифами, по стилю похожими на древнекитайское письмо VII-X века, периода правления династии Тан. [3]
Самый легкий способ справиться с умножением на 9 – это умножение на пальцах. (Приложение А, рис. 2 – 4)
Правила умножения на пальцах на 9:
Положите обе руки на стол перед собой.
Теперь мысленно нужно пронумеровать пальцы от 1 до 10 слева направо. Если мысленно тяжеловато, то напишите числа на бумаге.
Загибаем номер пальца на сколько нужно умножить число 9.
Результат делается следующим образом: п альцы, находящиеся слева от загнутого, обозначают десятки, а справа — единицы.
Пример: 9 · 4 получается 3 десятка и 6 единиц. То есть 36.
1.3.Японский метод умножения
Не секрет, что в разных странах методы преподавания разные. Несколько десятилетий назад самой сильной в мире системой школьного образования считалась советская. Но даже в СССР не использовали некоторые интересные методы обучения детей математике.
Например, в Японии ученики первого класса могут перемножать трёхзначные числа, не зная таблицу умножения. Для этого используется простейший метод с рисованием полосок . Логика метода понятна из рисунка.
Археологами в Японии была найдена деревянная табличка с фрагментом таблицы умножения, которая предположительно была изготовлена в VIII веке. Учёные полагают, что подобные таблицы использовались японскими императорскими чиновниками, которым было необходимо осваивать разные науки, в том числе и арифметику.
Обнаруженная табличка — самая древняя из всех найденных в Японии ранее. Интересно, что иероглифы, которыми записаны цифры, по стилю графического начертания очень похожи на те, которые использовались как официальное письмо во времена китайской династии Тан VII-X века. Исходя из этого, ученые предположили, что таблица была скопирована из китайского учебника арифметики того времени, то есть вся японская таблица умножения была заимствована из Китая. Именно к своим соседям в Китай ездили высокопоставленные японцы каждый год, чтобы перенять у них разные науки, такие как арифметику. Древняя китайская таблица умножения была не из простых, так как включала в себя умножение двузначных чисел друг на друга. Вряд ли все японские чиновники могли выучить такую таблицу наизусть, поэтому и носили с собой на работу что-то типа шпаргалок, фрагмент одной из которых и представляет собой найденная археологами в Японии табличка. [4]
Итак, японская таблица умножения была заимствована у китайцев, которые, согласно некоторым гипотезам, и были одними из создателей первой арифметической системы, о чем свидетельствуют археологические находки, содержащие фрагменты таблицы умножения, возраст которых ученые оценили в 2700-3000 лет.
Пример: вычислите 13 · 24 японским методом. Начертим следующий рисунок (Приложение А, рис. 5):
Первый множитель 13 значит, начертим одну горизонтальную линию (один десяток) и еще 3 горизонтальных линии (три единицы).
Второй множитель 24 значит, начертим две вертикальных линии (два десятка) и еще 4 линии (четыре единицы).
Результат: число единиц – количество точек (пересечение линий) в квадрате (12, т.е. пишем 2, а 1 идет в десятки); число десятков – количество точек в овале (10 + 1 = 1, значит пишем 1, а 1 идет в сотни); число сотен – количество точек к круге (2 + 1 = 3). Ответ: 312.
Глава 2. Практическая часть
2.1. Прибор для умножения
Шотландский математик Джон Непер придумал счетный прибор, состоящий из 10 палочек, предназначенный для умножения чисел. Устройство палочек основано на принципе итальянского умножения чисел. (Приложение А, рис. 6)
Рассмотрим алгоритм умножение многозначного числа на однозначное. Пусть, например, нужно вычислить произведение 258 · 8. [5]
1 шаг. Взять палочки и по первому ряду составить число. В нашем примере возьмём полоски с верхними цифрами 2, 5 и 8 и положим их рядом
2 шаг. Отсчитать сверху столько рядов, на сколько необходимо умножить. В рассматриваемом примере — восьмая строка.
3 шаг. Считаем по диагонали, прибавляя десятки к числу в следующей полосе.
В примере произведение равно 2064, еще один пример произведение 354 и 7 представлен на рисунке 7 (Приложение А).
«Палочками Непера» можно пользоваться и для умножения многозначных чисел. В книге «Математическая шкатулка» [3] объясняется данный способ. Необходимо выполнить указанный алгоритм для каждой цифры второго множителя и полученные результаты сложить.
Пусть нужно вычислить произведение 4375 · 347. Положим рядом 4 полоски с верхними числами 4; 3; 7; и 5. Определим произведение числа 4375 на 7. Получим 30 625. Умножим 4375 на 4 десятка получим 175000. Найдём ещё произведение 4375 на 3 сотни. Получим 13 125 сотен. Остаётся найти сумму получившихся произведений. 30 625 +175000+1312500=1518 125.
2.2. Собственный прибор для умножения
Мной был создан собственный прибор для умножения двухзначных чисел, который моделирует процесс умножения японским методом. Прибор выглядит следующим образом (Приложение Б, рис. 1 — 5) и состоит из деревянной рамки и надетой на нее в двух направлениях (вертикали и горизонтали) резинок. Общее количество резинок 36:
Работать с ним легко, как и с японским методом умножения. На каждой стороне рамки написаны цифры от 0 до 9 и сделаны небольшие отверстия для подсчета линий пересечений. (Приложение Б, рис. 1). Правая сторона – количество единиц, верхняя сторона – количество десятков, левая сторона – количество сотен, а нижняя сторона – число, которое переходит в следующий разряд. При умножении японским методом начинаем с подсчета количества единиц, затем десятков, а в конце сотен.
Ученые всегда стремились упростить вычисления, в том числе и умножение чисел. В книге Беллюстина В., написанной в 1969 году приводится 27 способов, в настоящее время появляются новые способы умножения. Умножение не стоит на месте, о чем доказывает новый способ умножения, который разработал Василий Иванович Оконешников. В каждое время у разных народов были свои способы умножения чисел. Как оказалось, японский метод умножения чисел не очень сложны в изучении и его можно применять на уроках математики.
Таким образом, поставленная цель исследования, а именно, изучить японский метод умножения и изготовить прибор для умножения двухзначных чисел, была достигнута. Выполнены следующие задачи исследования:
Провели поиск разных способов умножения чисел в литературных источниках.
Овладели различными способами умножения.
Освоили японский метод умножения двухзначных чисел.
Изготовили прибор для умножения, используя японский метод умножения двухзначных чисел.
Беллюстин В. Как постепенно люди дошли до настоящей арифметики.-М.: Педагогический листок, 1969.-112с.
Глейзер Г.И. История математики в школе.- М.: Просвещение, 1964.-375 с.
Нагибин Ф.Ф. Математическая шкатулка.-М.:Учпедгиз,1958.-167с.
Перельман Я.И. Занимательная арифметика,- М.: АО «Столетие»,1994.- 176 с.
Я познаю мир: Детская энциклопедия: Математика/ Сост. А.П. Савин,В.В. Станцо, А.Ю. Котова: Под общ. Ред. О.Г. Хинн. – М.: ООО «Фирма «Издательство АСТ», 1999.- 480 с.
Рис. 1.Таблица умножения
Рис. 3. Нумеруем пальцы
Рис. 4. Загибаем номер пальца на сколько нужно умножить 9
Рис.5. Японский метод умножения 13 · 24
Рис. 6. Счетные палочки Непера
Рис. 7. Умножение с помощью палочек Непера 354·7=2478
Рис. 1. Собственный прибор для умножения двухзначных чисел
Источник