Способы решения старинных задач
МБОУ «Чочунская СОШ имени И.М.Гоголева»
Способы решения старинных задач
Выполнила: учитель начальных классов
Ефремова Наталья Иннокентьевна
Способы решения старинных задач…………………………………………..
Список используемой литературы…………………………………
В обучении учащихся математике большая роль отводится текстовым задачам. Решение задач реализует не только образовательные, но и развивающие и воспитательные цели, т.е. играет важную роль в общем развитии их интереса к математике.
Существует множество старинных задач, которые предоставляют замечательную возможность проследить за развитием математической мысли с древнейших времен. Увлечение математикой часто начинается с размышлений над какой-то особенно понравившейся задачей. Она может встретиться на школьном уроке, на занятии математического кружка, на олимпиадах в журнале или в книжке.
Очень интересны старинные задачи, которые вошли в сборник Татьяны Прокопьевны Аммосовой «Математические олимпиады младших школьников в Республике Саха (Якутия)». У нас в школе ежегодно проводится улусная Аммосовская олимпиада по математике и в олимпиадных заданиях всегда даются старинные задачи.
Известные древнейшие задачи о переправах через реку, переливаниях жидкостей и другие с большой любовью и гордостью передаются из поколения в поколение. Задачи-сказки, задачи-рассказы и задачи со сказочными сюжетами очень нравятся детям младшего школьного возраста и способствуют развитию математического мышления.
Старинные задачи пришли к нам из глубины веков, от наших предков. Разные народы нашей планеты придумывали их, оттачивали условия и логику заданий. Они неизбежно остроумны и занимательны, в них собраны замечательные находки многих поколений. Еще в древние века математика занимала основное место в умах ученых, у нас есть возможность решать старинные задачи.
Об арифметике два с половиной века тому назад один из первых русских математиков-педагогов – Леонтий Филиппович Магницкий (1669-1739) писал, что это «художество частное, независимое и всем удобопонятное, многополезнейшее и многопохвальнейшее».
Старинные задачи позволяют не только развить смекалку и сообразительность, но и почувствовать прикосновение других эпох, порадоваться пришедшему решению точно так же, как когда-то, быть может, радовались наши предки. Наши предки умели думать и решать задачи. Очень многие сказки воспевают смекалку и скорость мышления, благодаря которым герои обретают счастье. Такие качества, как сообразительность, оригинальность слова и дела, уникальность и мастерство всегда были и будут в цене. Конечно, задач и головоломок за века было придумано неисчислимое множество.
Цель исследования: выявление роли и места старинных задач в современном мире, рассмотрение различных способов решения старинных задач.
исследовать решение старинных задач методом перебора; методом подбора; методом предположения, алгебраическим способом; наглядно-геометрическим способом.
Если поставлена цель решить конкретную математическую задачу, то обычно выбирается такой метод ее решения, который решающему представляется наиболее целесообразным, быстрее приводит к цели. Чаще используется тот метод, которым лучше владеет решающий.
Одну и ту же задачу разные решающие должны решать своим, индивидуальным способом и лишь после этого пытаться понять иные методы рассуждений. И. В. Гете говорил: «Каждый слышит только то, что понимает». Чтобы решить задачу, решающий всегда проходит ряд этапов: он должен понять задачу, поставить цель, которую впоследствии должен достичь, затем составить план, найти правильный путь решения, испробовать различные способы, сделать проверку.
Решение одной и той же задачи различными способами дает возможность полнее исследовать свойства и выявить наиболее простые решения. Нередко найденный способ решения в дальнейшем используется при решении более трудных задач. Разбор задач, допускающих много решений – увлекательное занятие, требующее знаний всех разделов школьной математики и длительной работы.
Способы решения старинных задач из олимпиадных заданий.
Сегодняшние дети удивляются находчивости, мудрости их предков. Иногда кажущиеся простыми на вид задачи требуют напряжение ума и воли. На примере задач рассмотрим различные способы решения.
У фермера имеются куры и кролики. Всего у этих кур и кроликов 5 голов и 14 ног. Сколько кур и кроликов имеет фермер?
Способы решения этой задачи. Есть 4 способа решения этой задачи:
1 способ: метод подбора:
2 кролика, 3 курицы.
2 способ: перебор вариантов
Решение таким методом лучше оформить в виде таблицы:
Источник
Старинные задачи и способы их решения
Старинные задачи позволяют не только развить смекалку и сообразительность, но и почувствовать прикосновение других эпох, порадоваться пришедшему решению точно так же, как когда-то, быть может, радовались наши предки. Наши предки умели думать и решать задачи. Очень многие сказки воспевают смекалку и скорость мышления, благодаря которым герои обретают счастье. Такие качества, как сообразительность, оригинальность слова и дела, уникальность и мастерство всегда были и будут в цене. Конечно, задач и головоломок за века было придумано неисчислимое множество, и я специально отобрал лучшие из них.
Содержимое разработки

Увлечение математикой часто начинается с размышлений над какой-то особенно понравившейся задачей. Она может встретиться и на школьном уроке, и на занятии математического кружка, и в журнале или книжке. А меня очень заинтересовали старинные задачи, с которыми мы столкнулись на уроке математики. И я решил узнать о них больше. Старинные задачи пришли к нам из глубины веков, от наших предков. Разные народы нашей планеты придумывали их, оттачивали условия и логику заданий. Они неизбежно остроумны и занимательны, в них собраны замечательные находки многих поколений.
Старинные задачи позволяют не только развить смекалку и сообразительность, но и почувствовать прикосновение других эпох, порадоваться пришедшему решению точно так же, как когда-то, быть может, радовались наши предки. Наши предки умели думать и решать задачи. Очень многие сказки воспевают смекалку и скорость мышления, благодаря которым герои обретают счастье. Такие качества, как сообразительность, оригинальность слова и дела, уникальность и мастерство всегда были и будут в цене. Конечно, задач и головоломок за века было придумано неисчислимое множество, и я специально отобрал лучшие из них.
Еще в древние века математика занимала основное место в умах ученых и благодаря сохранившимся рукописям у нас есть возможность проследить за развитием математической мысли и возможность прорешать старинные задачи и сравнить их решение с современным решением.
Цель исследования: выявление роли и места старинных задач в современном мире, рассмотрение различных способов решения старинных задач.
- исследовать решение старинных задач методом перебора; методом подбора; методом предположения, алгебраическим способом; наглядно-геометрическим способом
- исследовать старинный способ решения задач на сплавы и смеси.
Диофант умел решать
очень сложные уравнения,
он применял для этого
Жизнь Диофанта . По преданию, на могильном камне имелась такая надпись:
«Путник! Под этим камнем покоится прах Диофанта, умершего в глубокой старости. Шестую часть своей долгой жизни он был ребёнком, двенадцатую- юношей, седьмую- провёл неженатым. Через 5 лет после женитьбы у него родился сын, который прожил вдвое меньше отца. Через четыре года после смерти сына уснул вечным сном и сам Диофант, оплакиваемый своими близкими. Скажи, если умеешь считать, сколько прожил Диофант?»





Довольно часто приходится смешивать различные жидкости, порошки, разбавлять что-либо водой или наблюдать испарение воды. В задачах такого типа эти операции приходится проводить мысленно и выполнять расчёты. При решении задач на смеси считается, что рассматриваемые смеси однородны: не делается различия между литром как единицей массы и как единицей ёмкости. Концентрацией вещества называется отношение массы этого вещества к массе всей смеси (раствора, сплава). Концентрация вещества, выраженная в процентах, называется процентным отношением вещества в смеси (растворе, сплаве). Существует старинный способ решения задач на смеси и сплавы. Задачам подобного типа уделялось значительное внимание в старинных рукописях и «Арифметике» Л.Ф.Магницкого.
После определения числового выражения — переход на следующий слайд (верхняя кнопка)
Попадая повторно на этот слайд повторяем определение буквенных выражений. Далее: Чтобы получить второе определение – нажмите на «Знайку». После определения буквенных выражений нажмите на вторую кнопу и Вы перейдете к практическому заданию.
Лео́нтий Фили́ппович Магни́цкий (9(19)июня 1669- 19(30)октября 1739)
Магницкий Л.Ф. (при рождении Телятин)-
русский математик, педагог;
преподаватель математики в Школе
математических и навигацких наук
в Москве (с 1701 по 1739),
автор первой в России учебной
энциклопедии по математике
(в 1703г. «Арифметика»), которая
более ста лет являлась основным
учебным пособием по математике
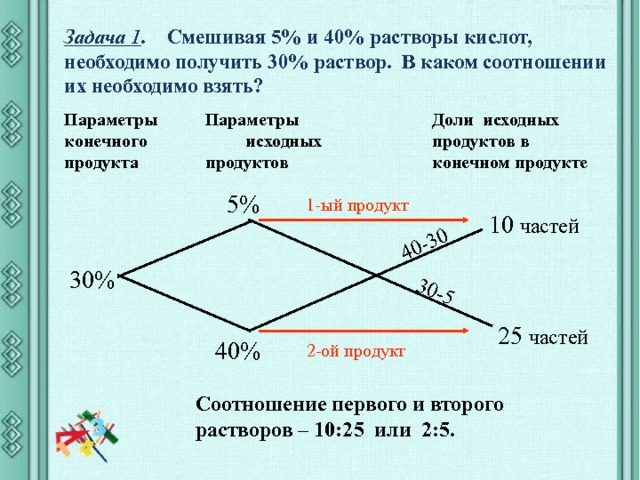
Задача 1 . Смешивая 5% и 40% растворы кислот, необходимо получить 30% раствор. В каком соотношении их необходимо взять?
Параметры конечного продукта
Параметры исходных продуктов
Доли исходных продуктов в конечном продукте
Соотношение первого и второго растворов – 10:25 или 2:5.
Задача 1а. Смешивая 5% и 40% растворы кислот, необходимо получить 30% раствор. Сколько грамм каждой кислоты необходимо смешать, чтобы получить 140 г 30%- ого раствора?
- Сколько грамм приходится на одну часть?
- Сколько грамм 5%-го раствора взять?
- Сколько грамм 40%-го раствора взять?
Ответ: для получения 140г 30%-ного раствора нужно
взять 5%-ного раствора 40г, а 40%-ного — 100 г.
Математика в настоящее время все шире проникает в повседневную жизнь, все более внедряется в традиционно далекие от нее области. Компьютеризация общества, внедрение современных информационных технологий требует математической грамотности человека почти на каждом рабочем месте. Это предполагает и конкретные математические знания, и определенный стиль мышления, вырабатываемый математикой.
Решение задач различными способами способствует углублению знаний, логического мышления, расширяет кругозор.
«Кто с детских лет занимается математикой, тот развивает внимание, тренирует свой мозг, свою волю, воспитывает настойчивость и упорство в достижении цели». (А. Маркушевич)
Ознакомление с историческими фактами позволяет лучше понять роль математики в современном обществе, углубляют понимание изучаемого раздела программы.
В результате изученной темы было выяснено, что существует множество методов различных старинных задач. Естественно, все их виды рассмотреть невозможно. Также мы научились правильно анализировать задачи и решать их разными методами (путём составления уравнений, т.е методом ложного положения, методом полного перебора вариантов и т.д) и разными способами: алгебраическим и арифметическим (старинным). Арифметические способы решения текстовых задач имеют больший развивающий потенциал, чем универсальный алгебраический способ решения. В наше время предпочтение отдаётся алгебраическому способу.
Источник
СТАРИННЫЕ ЗАДАЧИ С РЕШЕНИЯМИ
Из «Всеобщей арифметики» Исаака Ньютона
1 задача
Трое рабочих могут выполнить некоторую работу, при этом А может выполнить её один раз в три недели, В — три раза за 8 недель, С — 5 раз за 12 недель. За какое время они смогут выполнить эту работу все вместе?(в неделе 6 рабочих дней по 12 часов)
Решение
Рабочий А выполнит работу за 3*6*12=216(ч) Hабочий В выполнит работу за 8*6*12:3=192(ч) Рабочий С выполнит работу за 12*6*12:5=864/5(ч) За 1 час А выполнит 1/216 часть работы, В выполнит 1/192 часть работы, С выполнит 5/864 часть работы. Вместе за 1 час они выполнят 1/216+1/192+5/864=27/1728=1/64 часть работы. Тогда всю работу они выполнят за 1:1/64=64(ч) Ответ: за 64 часа
2 задача
Лев может съесть овцу за 2 часа, волк — за 3 часа, а собака — за 6 часов. За какое время они вместе съели бы овцу?
Решение
Лев за час съест1/2 часть овцы, Волк за час съест 1/3 часть овцы, Собака за час съест 1/6 часть овцы. вместе за час они съедят: 1/2+1/3+1/6=1(овцу) Ответ: они вместе съели бы овцу за 1 час.
3 задача
Некто желает распределить между бедными деньги. Если бы у него было на 8 динариев больше, то он мог дать каждому по 3, но он раздает лишь по два и у него остается 3. Сколько было бедных?
Решение
Пусть бедных — x, тогда 3х-8=2х+3 х=11 Ответ: было 11 бедных.
Из «Арифметики» Л.Ф.Магницкого (1703 г.)
1 задача
Некто согласился работать с условием получать в конце года одежду и 10 флоринов. Но по истечении 7 месяцев прекратил работу и при расчете получил одежду и 2 флорина. Во сколько ценилась одежда?
Решение
Пусть х флоринов стоит одежда, тогда (х+10)/12 — месячный заработок. 7(х+10)/12=х+2 7х+70=12х+24 5х=46 х=9,2 Ответ: одежда стоит 9,2 флорина
2 задача
Случися некоему человеку к стене лесницу приставить, стены же той высота 117 стоп. Имелась лестница длиною 125 стоп. На сколько стоп нижний конец сией лестницы от стены отставить?
Решение
При решении задачи используем теорему Пифагора. Длина лестницы — гипотенуза, высота стены известный катет, отступ нижнего конца лестницы от стены — неизвестный катет. 125*125-117*117=1936=44*44 Ответ: длина отступа равна 44 стопы.
3 задача
Купец имел 14 чарок серебряных, причем веса чарок растут по арифметической прогрессии с разностью 4. Последняя чарка весит 59 латов. Определить, сколько весят все чарки.
Решение
а14=а1+13d, a1=59-13*4=7 S14=(7+59)/2*14=462 Ответ: все чарки весят 462 лата
4 задача
Некий человек покупал масло. Когда он давал деньги за 8 бочек масла, то у него осталось 20 алтын. Когда же стал давать за 9 бочек, то не хватило денег полтора рубля с гривною. Сколько денег было у этого человека?
Решение
1 гривна=10 копеек, 1 алтын-3 копейки. Пусть бочка стоит х руб. 8х+0,6=9х-1,6 х=2,2 руб. до покупки у него было 2,2*8+0,6=18,2 руб Ответ: у человека было 18 рублей и 2 гривны
5 задача
Некто пришел в ряд, купил игрушек для малых ребят. За первую игрушку заплатил одну пятую своих денег, за другую три седьмых остатка от первой игрушки, за третью заплатил три пятых остатка от второй игрушки, а по приезде в дом нашел остальные — 1 рубль 92 копейки. Спрашивается, сколько в кошельке денег было и сколько за каждую игрушку он заплатил?
Решение
1-15=4/5 — остаток 4/5*3/7=12/35(денег) — за первую игрушку 4/5-12/35=16/35 — остаток от второй игрушки 16/35*3/5=48/175(денег) — стоит вторая игрушка 16/35-48/175=32/175 (денег) — осталось в кошельке 1,92:32/175=10,5(руб) — было в кошельке. 10,5*1/5=2,1(руб) — стоила 1 игрушка (10,5-2,1)*3/7=3,6(руб) — стоила 2 игрушка (8,4-3,6)*3/5=2,88(руб) — стоила 3 игрушка
6 задача
Говорит дед внукам: «Вот вам 130 орехов. Разделите их на 2 части так, чтобы меньшая часть, увеличенная в 4 раза, равнялась бы большей части, уменьшенной в 3 раза».Как же разделить орехи?
Решение
Уменьшив втрое количество орехов в большей части, мы получим их столько же, как в четырех меньших частях. Значит большая часть должна содержать в 3*4=12 раз больше орехов, чем меньшая, а общее число орехов должно быть в 13 раз больше, чем в меньшей, поэтому меньшая должна содержать 130/13=10 орехов, а большая 130-10=120 орехов. Ответ: 10 и 120 орехов.
Индусские задачи из Бхасхары
Задачи решаются составлением квадратного уравнения
1 задача
Цветок лотоса возвышался над поверхностью пруда на 4 фута, под напором ветра он скрылся под водой на расстоянии 16 футов от того места, где он раньше поднимался над водой. Какой глубины был пруд?
2 задача
На две партии разбившись Забавлялись обезьяны. Часть восьмая их в квадрате В роще весело резвилась, Криком радостным двенадцать Воздух свежий оглашали. Вместе сколько, ты мне скажешь, Обезьян там было в роще?
Задача из «Азбуки» Л.Н.Толстого (1828-1910 гг.)
Задача
Пятеро братьев разделили между собой наследство отца поровну. В наследстве было три дома. Три дома нельзя было делить, их взяли старшие три брата. Каждый из старших заплатил по 800 рублей меньшим. Меньшие разделили эти деньги между собой, и тогда у всех пяти братьев стало поровну. Много ли стоили дома?
Решение
800*3=2400(руб.) — заплатили двум меньшим; 2400:2=1200(руб.) — получил каждый в наследство; 1200*5:3=2000 — стоил дом. Ответ: дом стоил 2000 рублей.
Из рассказа А.П.Чехова «Репетитор»
Задача
Купец купил 138 аршин черного и синего сукна на 540 руб. Спрашивается, сколько аршин купил он того и другого, если синее стоило 5 рублей за аршин, а черное — 3 рубля.
Решение
Пусть синего сукна было х аршин, тогда черного (138-х) аршин. 5х+3(138-х)=540 5х+414-3х=540 2х=126 х=63(аршина) — синего 138-63=75(аршин) черного. Ответ: синего 63 аршина, черного 75 аршин.
Старинные задачи
1 задача
Скупой богач раздобыл 9 одинаковых монет, но, зная, что одна из них фальшивая и легче других, мучился до самой смерти, однако так и не додумался, как отличить, какая именно. Тем не менее даже самый начинающий мудрец, подумав, должен найти способ всего двумя взвешиваниями на весах без гирь определить фальшивую монету.
Решение
Разделить 9 монет на 3 группы по 3 монеты. Кладем по 3 монеты. Кладем по три монеты на чашки весов. Если весы в равновесии, то фальшивая монета в третьей кучке. Тогда берем две из трех монет и кладем их по одной на чашки. Если весы в равновесии, то легкая монета третья, если нет, то одна чашка поднимется — там фалтшивая.
2 задача
У одного старика спросили сколько ему лет. Он сказал, что ему сто лет и несколько месяцев, но дней рождения у него было всего 25. Как это могло быть?
Решение
Он родился в високосный год 29 февраля.
3 задача
Летела стая гусей, навстречу ей — один гусь. Говорит гусь: «Здравствуйте, 100 гусей!» А вожак стаи в ответ: «Нас не 100 гусей. Вот было бы нас столько, сколько теперь, да еще столько, да еще полстолько, да четверть столько, да еще ты, гусь, вот тогда нас было бы 100.» Сколько было гусей в стае?
Решение
Пусть было х гусей. Составим уравнение: х+х+0,5х+0,25х+1=100 2,75х=99 х=36 Ответ: в стае 36 гусей.
4 задача
Роскошнолипа расцветала Под ней червяк завелся малый. Да вверх пополз во всю он мочь — Четыре локтя делал в ночь. Но днем со слепу поз обратно Он на два локтя аккуратно Трудился наш червяк отважный, И вот итог работы важной, Награда девяти ночей: мОн на верхушке липы сей. — Теперь, мой друг, поведай ты, Какой та липа высоты?
Решение
(4-2)8+4=20 Ответ: высота липы 20 локтей
5 задача
Послан человек из Москвы в Вологду, и велено ему в хождении своем совершать каждый день по 40 верст. На следующий день вслед ему послан второй человек, и приказано ему делать в день по 45 верст. На какой день второй человек догонит первого?
Решение
Так как первый вышел на день раньше и прошел 40 верст, то второму надо нагнать эти 40 верст. 40:(45-40)=8 дней Ответ: за 8 дней второй человек догонит первого.
6 задача
Идет один человек в другой город и проходит в день по 40 верст, а другой человек идет из другого города ему на встречу и проходит в день по 30 верст. Расстояние между городами 700 верст. Через сколько дней путники встретятся?
Решение
За один день путники сближаются на 30+40=70 верст. 700:70=10 дней Ответ: через 10 дней путники встретятся.
7 задача. (задача Бируни)
Если 10 дирхемов (денежная единица) приносят доход 5 дирхемов за 2 месяца, то какой доход принесут 8 дирхемов за 3 месяца.
Решение
10 дирхемов — 2,5 дирхема за 1 месяц 8 дирхемов — х дирхемов за 1 месяц 10/8=2,5/x x=8*2,5/10 x=2 2*3=6 Ответ: 8 дирхемов принесут доход 6 дирхемов за 3 месяца
8 задача (Китай II век)
Дикая утка от южного моря до северного моря летит 7 дней, а дикий гусь от северного моря до южного моря летит 9 дней. Теперь дикая утка и дикий гусь вылетают одновременно. Через сколько дней они встретятся?
Решение
1/7+1/9=16/63 1:16/63=63/16=3,9375 Ответ: через 3,9375 дня они встретятся.
9 задача
— Скажи мне, знаменитый Пифагор, сколько учеников посещает твою школу и слушает твои беседы? — Вот сколько, — ответил философ, — половина изучает математику, четверть — музыку, седьмая часть пребывает в молчании, кроме того, есть еще три женщины.
Решение
Пусть школу посещают х учеников, 1/2x+1/4x+1/7x+3=x x=28 Ответ: 28 учеников посещают школу Пифагора.
Задача из «Курса чистой математики» Войтяховского (1811 г.)
1 задача
Бутылка с пробкой стоят 12 копеек. Бутылка стоит на 10 копеек дороже, чем пробка. Сколько стоит бутылка и сколько пробка?
Решение
Пусть пробка стоит х копеек, тогда бутылка стоит (х+10) копеек. х+(х+10)=12 2х=2 х=1(коп) — стоит пробка. 1+10=11 (коп) — Стоит бутылка Ответ: пробка стоит 1 копейка, бутылка — 10 копеек.
2 задача
Разносчик продал первому покупателю половину имевшихся у него апельсинов и еще пол-апельсина, второму пкупателю — половину оставшихся апельсинов и еще пол-апельсина. Таким же образом продал он апельсины и остальным покупателям. Когда же подошел седьмой покупатель, то у разносчика уже ничего не осталось. Сколько апельсинов было у разносчика и сколько взял каждый покупатель?
Решение
1)Сколько всего было апельсинов? (((((0,5*2+0,5)*2+0,5)*2+0,5)*2+0,5)*2+0,5)*2=63 (а) 2)Сколько взял первый покупатель? 63:2+0,5=32 (а) 3)Сколько взял второй покупатель? (63-32):2+0,5=16 (а) 4)Сколько взял третий покупатель? (63-32-16):2+0,5=8 (а) 5)Сколько взял червертый покупатель? (63-32-16-8):2+0,5=4 (а) 6)Сколько взял пятый покупатель? (63-32-16-8-4):2+0,5=2 (а) 7)Сколько взял шестой покупатель? (63-32-16-8-4-2):2+0,5=1 (а)
3 задача
Собака усмотрела в 150 саженях зайца, который пробегает в 2 минуты по 500 саженей, а собака в 5 минут 1300 саженей. Спрашивается в какое время собака догонит зайца?
Решение
500:2=250 (саженей/мин) — скорость зайца 1300:5=260 (саженей/мин) — скорость собаки 150:(260-250)=15 (Мин) Ответ: через 15 минут собака догонит зайца.
Источник