- Информационно-коммуникационные технологии в педагогическом образовании
- НЕСКОЛЬКО СПОСОБОВ ИЗВЛЕЧЕНИЯ КВАДРАТНЫХ КОРНЕЙ
- К. Б. Милюхина
- НЕСКОЛЬКО СПОСОБОВ ИЗВЛЕЧЕНИЯ КВАДРАТНЫХ КОРНЕЙ
- Комментарии: 1
- Научно-исследовательская работа на тему: «Тайна квадратного корня»
- Содержание:
- Введение.
- Теоретические основы квадратного корня.
- История возникновения.
- Математика на глиняных табличках
- Квадратный корень из пирамиды Хеопса
- Геометрия племен майя
- Великие ученые не нашей эры
- В V веке до н. э. астроном, врач и математик Гиппократ написал первый учебник по геометрии, в котором ввел и объяснил множество математических формул и терминов, в том числе «гиппократовы луночки», при помощи которых пытался вычислить квадратуру круга.
- «Арифметика» Диофанта
- Происхождение термина и символики.
- Применение квадратного корня в других науках.
- Квадратный корень в элементарной геометрии
- Рис. 1
- Решение. По теореме Пифагора имеем
- Так как , т. е. расстояние равно 20 м.
- Квадратный корень в информатике
- Способы извлечения квадратного корня.
- Арифметический способ
- На мой взгляд, недостатком такого способа является то, что если извлекаемый корень не является целым числом, то можно узнать только его целую часть, но не точнее и при увеличении числа увеличивается громоздкость вычислений.
- Геометрический
- Метод Герона
- Второй метод Герона
- =≈≈5,3
- Метод Ньютона
- Метод подбора.
- Цифры
- Следовательно, наше число либо 52, либо 58
- Столбиком
- Возьмём число 56789,321
- Вывод
- Это интересно.
- По объективным математическим причинам этот праздник может отмечаться строго девять раз в столетие (семь раз в первой половине века и дважды — во второй), всегда в одни и те же дни:
- Приложение.
- Диофант Александрийский
- Прах Диофанта гробница покоит; дивись ей и камень
Информационно-коммуникационные технологии
в педагогическом образовании
НЕСКОЛЬКО СПОСОБОВ ИЗВЛЕЧЕНИЯ КВАДРАТНЫХ КОРНЕЙ
К. Б. Милюхина
Муниципальное бюджетное общеобразовательное учреждение Лесоперевалочная СОШ № 2, с. Бельтирское, Аскизский район
НЕСКОЛЬКО СПОСОБОВ ИЗВЛЕЧЕНИЯ КВАДРАТНЫХ КОРНЕЙ
Аннотация. Тема, затронутая в статье, показывает, что изучение квадратных корней, не прихоть математиков, а объективная необходимость: в реальной жизни случаются ситуации, математические модели которых содержат операцию извлечении квадратного корня. Изучив способы извлечения квадратного корня, был создан проект «Несколько способов извлечений квадратных корней».
1-й способ: Способ разложения на простые множители [1]
Для извлечения квадратного корня можно разложить число на простые множители и извлечь квадратный корень из произведения (табл.).
Ученики применяют этот способ успешно и считают единственным. Извлечение корня разложением на множители – трудоёмкая задача, которая не всегда приводит к желаемому результату. Попробуем извлечь квадратный корень из числа 206116. Разложение на простые множители дает произведение 2∙2∙51529. А как быть дальше? В ответе записывают остаток от разложения под знак корня. Чаще мы видим, что корень до конца не извлечь. Поэтому, этот способ лишь частично решает проблему извлечения квадратного корня.
2-й способ: Способ использования таблицы квадратов двузначных чисел [1]
Способ очень прост в применении и даёт мгновенное извлечение квадратного корня из любых целых чисел от 1 до 100 с точностью до десятых.
Найдём значение 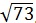
Закрываем две последние цифры у всех чисел в таблице квадратов и находим близкие для 73, таких два числа 7225 и 7396 (7396-это много). Рассматриваем число 7225.
Левый столбик таблицы квадратов даёт ответ 8 (целых), а верхняя строка 5 (десятых). Значит 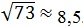
Быстро, просто, доступно на экзамене. Корни большие 100 этим способом извлечь невозможно. Способ удобен для заданий с маленькими корнями и при наличии таблицы.
3-й способ: Формула Древнего Вавилона [4]
Древние вавилоняне пользовались следующим способом нахождения приближенного значения квадратного корня из числа Х.
Число Х они представляли в виде суммы 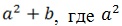
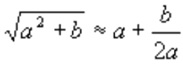
Извлечём с помощью этой древней формулы корень квадратный из числа 68:
Результат извлечения корня из 68 с помощью МК равен 8,246211.
Результат извлечения корня из 94 с помощью МК равен 9,695359.
Как видим, способ вавилонян даёт хорошее приближение к точному значению корня. Но без знания полных квадратов больших чисел и умения их быстро находить, результат извлечения будет найти затруднительно.
Этот способ являются самым простым и доступным для учащихся школ.
4-й способ: С помощью уравнения [2]
Существует удобный способ нахождения квадратного корня с помощью решения уравнения. В чем его суть рассмотрим на примере и попробуем вычислить значение корня из числа 37.Сначала определим границы искомого корня в целых числах. Легко догадаться, что это числа 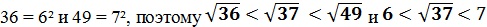
Пусть х – это та разница, на которую отличны друг от друга 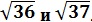
значит 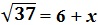
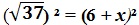
37 = (6 + х)² = 36 + 12х + х².
Так как мы рассчитываем получить результат с точностью до десятых или до сотых, а х² явно достаточно малая дробь, то ей вполне можно пренебречь.
В результате приходим к простому линейному уравнению 37 = 36 + 12х.
Решив его, получаем значение: х = 0,08. Значит 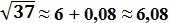
Но и этот способ требует терпения и умения решать уравнения с использованием формул сокращённого умножения.
5-й способ: Канадский метод [5]
Канадский метод был открыт молодыми учёными одного из ведущих университетов Канады в 20 веке. Его точность – не более двух-трёх знаков после запятой. Применяли формулу:
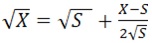
где X — число, из которого необходимо извлечь квадратный корень, а S — число ближайшего точного квадрата.
Например: извлечь квадратный корень из 86
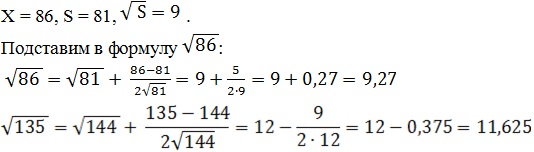
Метод несложный и удобный.
6-й способ: Способ вычетов нечётного числа [3]
Способ вычетов нечётного числа заключается в том, чтобы из подкоренного выражения последовательно вычитать нечётные числа 1, 3, 5, 7 и т. д. пока разность не станет равной 0, а затем подсчитать количество вычитаний. Это и будет ответ.
Например: извлечь квадратный корень из 81.
Решение: 81-1=80-3=77-5=72-7=65-9=56-11=45-13=32-15=17-17=0, количество вычитаний = 9, поэтому 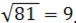
Например: извлечь квадратный корень из 225.
количество вычитаний = 15, поэтому 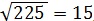
Российские учёные называют этот метод арифметическим извлечением квадратного корня, а за глаза «методом черепахи» из-за его медлительности. Недостатком такого способа является то, что если извлекаемый корень не является целым числом, то можно узнать только его целую часть, но не точнее. В то же время такой способ вполне доступен детям, решающим простейшие математические задачи, требующие извлечения квадратного корня.
7-й способ: Способ отбрасывания полного квадрата (для четырёхзначных чисел) [3].
Этот способ применим только для извлечения квадратного корня из точного квадрата, а алгоритм нахождения зависит от величины подкоренного числа.
1) Извлечение корней до числа
Например: 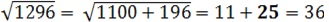
Число 1296 представим в виде суммы, выделив из этого числа квадрат 196, затем выделенный квадрат отбрасываем, к числу сотен первого слагаемого (11) прибавляем всегда 25. Получим ответ 36.
Так можно извлекать только квадратные корни до числа
2) Извлечение корней после числа
Например: 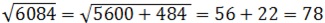
Число 6084 представим в виде суммы 5600 и выделенного квадрата 484. Затем к числу сотен прибавить квадратный корень из 484, равный 22.
Получим ответ 78.
Этот способ очень интересен и оригинален.
Применим только для четырёхзначных чисел точных квадратов.
Список литературы
- Мордкович, А. Г. Алгебра. 8 кл.: В двух частях. Ч.1: Учебник для общеобразовательных учреждений [Текст]. / А. Г. Мордкович. – М.: Мнемозина. – 2012.
- Пичугин, Л. Ф. За страницами учебника алгебры. Книга для учащихся 7–9 классов средней школы [Текст]. / Л. Ф. Пичугин. – М.: Просвещение. – 1990.
- Научно-теоретический и методический журнал «Математика в школе», 1998. – № 6.
- Теорема [Электронный ресурс]. // Википедия: свободная энциклопедия. – Режим доступа : http://ru.wikipedia.ord/wiki/Теорема
- Открытый урок [Электронный ресурс]. // Первое сентября. – Режим доступа : http://festival.1september.ru/
Научный руководитель: учитель математики
Сердюк С. А.
Комментарии: 1
| Андрей из Чебоксар 28.05.2020 в 19:15 |
5-й способ: Канадский метод
Так и хочется дописать:
Канадский метод был открыт молодыми учёными одного из ведущих университетов ДРЕВНЕГО ВАВИЛОНА (см. способ 3)
Источник
Научно-исследовательская работа на тему: «Тайна квадратного корня»
МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА № 55
СОВЕТСКОГО РАЙОНА ГОРОД ВОРОНЕЖ
«Тайна квадратного корня»
Содержание:
Введение. Теоретические основы квадратного корня. История возникновения. Применение квадратного корня в других науках. Способы извлечения квадратного корня. Выводы. Это интересно. Приложение. Литература.
Введение.
Перейдя в восьмой класс, мы познакомились с квадратными корнями. В ходе решения некоторых математических задач приходится оперировать с ними, но ведь не всегда корень можно вычислить просто заглянув в таблицу квадратов, не всегда число рационально, а квадрантные корни встречаются в огромном числе и в ряде других наук. Поэтому и были придуманы многочисленные формулы и способы извлечения квадратного корня, некоторые из которых относят к Древней Греции, к Вавилону, Древнему Египту.
Также меня заинтересовала история их появления, которая чем-то была похожа на историю изобретения колеса, ведь привычный нами термин и его графическое обозначение прошли много веков, перед тем как стать такими, какими мы привыкли их видеть.
Теоретические основы квадратного корня.
Квадратный корень из а — это решение уравнения: х2=a. Иначе говоря, квадратный корень из 



Пример для вещественных чисел: , ; потому чтоизквадратного корня существуют противоположные, т. е. отличающиеся знаком значения (в данном примере, положительное и отрицательное числа), и это затрудняет работу с корнями. Чтобы обеспечить однозначность, вводится понятие арифметического корня, значение которого при 
Квадратный корень является элементарной функцией.
Свойства графика функции 
Область определения функции — луч[0;+∞); у=0 при x=0; y>0 при x>0; функция возрастает на луче[0;+∞); унаим = 0 при х = 0, унаиб не существует; функция непрерывна и выпукла вверх.
История возникновения.
Необходимость математических вычислений при строительстве любых больших сооружений определило появление квадратного корня. Например, узнать длину диагонали любого прямоугольника возможно только, извлекая квадратный корень из суммы квадратов длин двух сторон.
Математика на глиняных табличках
Город Вавилон (Врата Бога) с населением полтора тысяч человек был основан в Междуречье более 3000 лет до н. э. На раскопках этого древнего поселения были найдены глиняные таблички с нанесенными на них знаками. Их возраст превышает 5000 лет. Когда были расшифрованы символы клинописи, археологи с изумлением прочитали уравнения вычисления различных площадей с помощью квадратных корней. Не известие об открытии, а уже его использование. Имя великого математика, первым догадавшегося извлечь квадратный корень, утеряно для истории.
Первые задачи, связанные с извлечением квадратного корня, обнаружены в трудах вавилонских математиков (о достижениях древнего Египта в этом отношении ничего не известно). Среди таких задач:
• Применение теоремы Пифагора для нахождения стороны прямоугольного треугольника по известным двум другим сторонам.
• Нахождение стороны квадрата, площадь которого задана.
• Решение квадратных уравнений.
Вавилонские математики (II тысячелетие до н. э.) разработали для извлечения квадратного корня особый численный метод.
Квадратный корень из пирамиды Хеопса
Как любое великое открытие, оно возникло одновременно в нескольких местах в головах разных гениальных людей. Например, в 2500 гг. до н. э. в Древнем Египте возводились пирамиды – усыпальницы фараонов. Археологи просчитали, что без знания числа р и квадратного корня построить такие сооружения с четко выстроенными коридорами и строгой ориентацией помещений по сторонам света было просто невозможно. И снова даже граффити на стенах каменных блоков не донесли до современности имен гениальных математиков.
Геометрия племен майя
Если Шумерская цивилизация еще могла как-то перетечь на Африканский континент, то математика племен майя в Южной Америке в это же время развивалась совершенно обособленно. Дворцы, возводимые в южноамериканских джунглях, не могли быть построены без знаний математики (квадратного корня в том числе), астрономии и даже основ оптики.
Великие ученые не нашей эры
В V веке до н. э. астроном, врач и математик Гиппократ написал первый учебник по геометрии, в котором ввел и объяснил множество математических формул и терминов, в том числе «гиппократовы луночки», при помощи которых пытался вычислить квадратуру круга.
Древнегреческому математику Эвклиду в III веке до н. э досталась великая миссия сублимировать мудрость предков, работы Гиппократа, изложить все в своих трудах «Начала», объяснив между прочим значение квадратного корня, и донести до последующих поколений.
«Арифметика» Диофанта
Спустя 600 лет в той же Греции Диофант Александрийский, основываясь на работах своих предшественников, ввел математические обозначения, которые человечество использует и сегодня, описал решения неопределенных уравнений, ввел понятия рациональных и иррациональных чисел. Им было написано 13 трактатов «Арифметика», только 6 из которых сохранились. В этих трудах великий грек объясняет решения уравнений с двумя неизвестными второго порядка, используя для их решений извлечение квадратного корня из числа, как давно известное математическое действии.
Аналогичные задачи и методы встречаются в древнекитайской «Математике в девяти книгах». Древние греки сделали важное открытие: иррациональное число. Детальное исследование, выполненное ТеэтетомАфинским (IV век до н. э.), показало, что если корень из натурального числа не извлекается нацело, то его значение иррационально.
Алгоритмы извлечения корней любой степени из целого числа, разработанные индийскими и исламскими математиками, были усовершенствованы в средневековой Европе. Николай Орем (XIV век) впервые истолковал корень 2-й степени как возведение в степень.
Комплексные корни произвольной степени в начале XIX века глубоко исследовал Гаусс, хотя первые результаты принадлежат Эйлеру. Чрезвычайно важным открытием (Галуа) стало доказательство того факта, что не все алгебраические числа (корни многочленов) могут быть получены из натуральных с помощью четырёх действий арифметики и извлечения корня.
Происхождение термина и символики.
Термин корень имеет долгую и сложную историю. Извлечение квадратного корня древние греки понимали строго геометрически: как нахождение стороны квадрата по известной его площади. После перевода на санскрит греческое слово «сторона» превратилась в «мула» (основание). Слово «мула» имело также значение «корень», поэтому при переводе индийских сиддхант на арабский использовался термин «джизр» (корень растения). Впоследствии аналогичное по смыслу слово «radix» закрепилось в латинских переводах с арабского, а через них и в русской математической терминологии («корень», «радикал»).
Средневековые математики (например, Кардано) обозначали квадратный корень символом Rx, сокращение от слова «radix». Современное обозначение впервые употребил немецкий математик Кристоф Рудольф, из школы коссистов (то есть алгебраистов), в 1525 году. Происходит этот символ от стилизованной первой буквы того же слова «radix». Черта над подкоренным выражением вначале отсутствовала; её позже ввёл Декарт (1637) для иной цели (вместо скобок), и эта черта вскоре слилась со знаком корня.
Из всей истории появления в математике квадратного корня получается, что патент на изобретение квадратичных исчислений, так же, как и на изобретение колеса, выдавать некому.
Применение квадратного корня в других науках.
Квадратный корень применяется в числе многих наук.
Квадратный корень в элементарной геометрии
Квадратные корни тесно связаны с элементарной геометрией: если дан отрезок длины 1, то с помощью циркуля и линейки можно построить те и только те отрезки, длина которых записывается выражениями, содержащими целые числа, знаки четырёх действий арифметики, квадратные корни и ничего сверх того.
К извлечению квадратных корней сводятся многие геометрические задачи. Например, в курсе геометрии доказывают теорему Пифагора: квадрат длины гипотенузы прямоугольного треугольника равен сумме квадратов длин катетов этого треугольника. Индийцы две тысячи леттому назад доказывали ее с помощью следующего чертежа:
Рис. 1
Видим, что площади заштрихованных фигур в обоих квадратах равны, но в одном случае площадь равна 


Из теоремы Пифагора следует
с =
Пример 1. Найдем расстояние от вершины дерева до конца его тени, если высота дерева равна 12 м, а длина тени – 16 м.
Решение. По теореме Пифагора имеем
Так как  , т. е. расстояние равно 20 м.
, т. е. расстояние равно 20 м.
Квадратный корень в информатике
Во многих языках программирования функционального уровня функция квадратного корня обозначается как sqrt (от англ. squareroot «квадратный корень»). Эта функция широко применяется в среде MS Exele, при исследовании и построении графиков квадратичной функции, в средах объектно-ориентированных языках (Delfy, Visual Basic и др.).
В физике любая формула, содержащая величину возведённую в квадрат при извлечении которойпридётся вносить величины под знак квадратного корня например 

В химии и биологии позаимствовано лишь название: радикал — группа атомов, содержащая углеводородный остаток в молекуле.
В истории и психологии радикал — сторонник резких решений, а так же его синонимы радикальный, радикализм и т. д.
Способы извлечения квадратного корня.
В ходе данного исследования мною было обнаружено несколько способов извлечения квадратного корня:
Арифметический Геометрический Метод Герона Метод Ньютона Столбиком Метод подбора.
Арифметический способ
Для квадратов чисел верны следующие равенства:
То есть, узнать целую часть квадратного корня числа можно, вычитая из него все нечётные числа по порядку, пока остаток не станет меньше следующего вычитаемого числа или равен нулю, и посчитав количество выполненных действий. Например, так:
Выполнено 3 действия, квадратный корень числа 9 равен 3.
На мой взгляд, недостатком такого способа является то, что если извлекаемый корень не является целым числом, то можно узнать только его целую часть, но не точнее и при увеличении числа увеличивается громоздкость вычислений.
Геометрический
К извлечению квадратных корней сводятся многие геометрические задачи.
Например, в курсе геометрии доказывают теорему Пифагора: квадрат длины
гипотенузы прямоугольного треугольника равен сумме квадратов длин катетов
этого треугольника. Индийцы две тысячи лет тому назад доказывали ее с
помощью следующего чертежа.
Видим, что площади заштрихованных фигур в обоих квадратах равны, но в
одном случае площадь равна


Квадратный корень можно вычислить при помощи этого чертежа:
|BH|=
В частности, если
Метод Герона
Следующий метод, который мы изложим, был известен ещё в Древней
Греции и приписывается Герону Александрийскому. Герон жил в I веке н. э. и описал в своих книгах закон отражения света, формулу вычисления площади треугольника по трём сторонам, многочисленные механизмы. Интересно, что и в наше время метод Герона используется некоторых вычислительных машинах (может быть, и в вашем калькуляторе!). Обратимся к тексту самого Герона. Он объясняет свой метод на примере: пусть надо найти корень из 720.
Так как 720 не имеет рационального корня, то возьмем корень с очень малой погрешностью следующим образом. Так как ближайший к 720 квадрат есть 729, и оно имеет корнем 27, то раздели 720 на 27. Получается 26
26

Разделим результат на 2, получим 26


Второй метод Герона
Древние вавилоняне пользовались следующим способом нахождения приближенного значения квадратного корня их числа х. Число х они представляли в виде суммы 



Извлечем с помощью формулы корень квадратный, например из числа 28

 =
=
 ≈
≈
 ≈5,3
≈5,3
Возведем в квадрат полученный результат
Погрешность составляет 0,09 единицы.
Метод Ньютона
Еще 4000 лет назад вавилонские ученые составляли наряду с таблицами умножения и таблицами обратных величин (при помощи которых деление чисел сводилось к умножению) таблицы квадратов чисел и квадратных корней из чисел. При этом они умели находить приблизительное значение квадратного корня из любого целого числа. Вавилонский способ приближенного вычисления квадратных корней можно иллюстрировать на следующем примере, изложенном в одной из найденных при раскопках клинописных табличек.
Вычислим 
Предположим, что мы имеем некоторое приближенное значениеx0 числа
x0 =1 надо сравнить с числом 



















Это приближение x1 можно улучшить таким же способом, то есть взять среднее арифметическое чисел 

Как видим, уже пятое приближение не отличается (при вычислениях с девятью знаками после запятой) от четвертого. Итак, 

Метод подбора.
В нем всего лишь три шага но с его помощью можно извлекать только корни из рациональных чисел и при этом только от 100 до 10 000. Для примера возьмём число 3364
Ограничить корень числами кратными десяти, наше число находится между 

Последняя цифра корня взаимосвязана с последней цифрой подкоренного выражения.
Цифры
Последние цифры их квадрата
Следовательно, наше число либо 52, либо 58
Столбиком
Возьмём число 56789,321
1. Разбиваем его цифры на пары: те, что стоят слева от десятичной запятой, группируем по две справа налево, а те, что правее – по две слева направо. Получаем 5,67,89.32,1 .
2. Извлекаем квадратный корень из первой группы цифр слева – в нашем случае это 5 (ясно, что точно корень может не извлекаться, берем число, квадрат которого максимально близок к нашему числу, образованному первой группой цифр, но не превосходит его). В нашем случае это будет число 2 . Записываем 2 в ответ – это старшая цифра корня.
3. Возводим число, которое стоит уже в ответе — это 2 — возводим в квадрат и вычитаем из первой слева группы цифр – из числа 5 . В нашем случае остается 1 .
4. Приписываем справа следующую группу из двух цифр: 167 . Число 2 , которое уже стоит в ответе, умножаем на 2 , получаем 4 .
5. Нам нужно к числу 4 справа приписать одну цифру




6. Из 167 вычитаем произведение 43 * 3 , получаем 38 .
7. Далее повторяем знакомые операции: приписываем к справа следующую группу цифр 89 , умножаем 23 на 2 , к полученному числу приписываем справа одну цифру, такую, чтобы при умножении на нее получилось число, меньшее 3889 , но наиболее близкое к нему – это цифра 8 – следующая цифра в десятичной записи корня.
8. Далее у нас в числе стоит десятичная точка, ставим такую же в результате после цифры. Продолжаем процесс, снося по две цифры после точки. Ясно, что можно сносить и два нуля.
Вывод
Как любое великое открытие, оно возникло одновременно в нескольких местах в головах разных гениальных людей, и отдать его некому, а само появление квадратных корней – не прихоть математиков, а объективная необходимость решения реальных жизненных ситуаций, математические модели которых содержат операцию извлечения квадратного корня. Квадратный корень имеет историю в несколько десятков веков, а способы его извлечения возникли почти с появлением самого корня во всех частях света еще в древности, но остаются актуальны и по сей день ведь не всегда мы имеем под рукой калькулятор.
В предисловии к своему первому изданию “В царстве смекалки” пишет: “. умственную самодеятельность, сообразительность и «смекалку” нельзя ни “вдолбить”, ни “вложить” ни в чью голову. Результаты надёжны лишь тогда, когда введение в область математических знаний совершается в лёгкой и приятной форме, на предметах и примерах обыденной и повседневной обстановки, подобранных с надлежащим остроумием и занимательностью”. Я не могу не согласиться с известным русским математиком, так как в математике следует помнить не формулы, а процесс мышления.
Это интересно.
Во время работы над данным исследованием мною была обнаружена интересная информация. Оказывается, существует неофициальный праздник, посвященный квадратному корню.
День квадратного корня — праздник, отмечаемый девять раз в столетие: вдень, когда и число, и порядковый номер месяца являются квадратными корнями из двух последних цифр года (например, 2 февраля 2004 года: 02-02-04).
Впервые этот праздник отмечался 9 сентября 1981 года (09-09-81).
Основателем праздника является школьный учитель Рон Гордон из города Редвуд Сити, Калифорния, США. По состоянию на 2010 год Гордон продолжает публиковать заметки о придуманном им празднике, активно контактируя поэтому поводу со СМИ. Его дочь с помощью Facebook собрала группу поклонников этого праздника, где каждый может поделиться своим способом отметить эту необычную дату.
Главным блюдом на этом «праздничном столе» обычно являются вареные кубики из корнеплодов и выпечка в форме математического знака квадратного корня
По объективным математическим причинам этот праздник может отмечаться строго девять раз в столетие (семь раз в первой половине века и дважды — во второй), всегда в одни и те же дни:
2 февраля хх04 года
5 мая хх25 года
9 сентября хх81 года
При этом интересно заметить, что промежуток (в годах) междупраздниками составляет непрерывную последовательность нечётных чисел: 3, 5,7 и т. д.
Ближайший такой праздник будет 4 апреля 2016 года
Приложение.
Гиппократ (ок. 460 — ок. 377 до н. э.)
Имя прославленного древнегреческого врача Гиппократа известно сегодня даже тем, кто имеет весьма отдаленное отношение к медицине, ведь и по сей день, получая диплом медика, профессионалы дают клятву, названную в его честь. Известно, что Гиппократ — уроженец греческого острова Кос, находящегося в восточной части Эгейского моря, где он появился на свет примерно в 460 г. до н. э. Он был продолжателем рода асклепиадов, династии врачей, основатель которой, легендарный Асклепий (Эскулап) впоследствии был признан богом медицины.
С молодых лет он много времени посвящал путешествиям, пополняя багаж знаний информацией о практике врачей стран, в которых ему доводилось бывать. Умер отец медицины примерно в 377 г. до н. э. (в других источниках – 370 г. до н. э.). Его последним пристанищем стала Фессалия, город Ларисса.
Гиппократ был не просто врачом от бога – именно им были заложены основы медицины, реформированы существовавшие в его время многие постулаты. Существует т. н. Гиппократовский корпус – сборник, состоящий из 60 трактатов, из которых, впрочем, только, по разным данным, от 8 до 18 были написаны самим легендарным врачом.
Гиппократ был в числе первых врачевателей, которые исключали из возможных причин болезней религиозный фактор — гнев богов, бывший в большом ходу у его современников. По сей день используются приемы перевязок и инструменты, о которых говорилось в трудах Гиппократа, посвященных хирургии, что является свидетельством высокого уровня развития в эпоху античности этой области медицины.
Гиппократ заложил фундамент рациональной диетологии, предложил отличающиеся системы питания для разных форм заболеваний, стал первым, кто пользовался ощупыванием, простукиванием, слушанием для диагностики; активно практиковал массаж, банки, кровопускание, лечебные ванны. При всем новаторстве подходов главным принципом деятельности Гиппократа был «Не навреди!», призывающий врачей соблюдать осторожность в лечении больных. В ряде трудов призывал он коллег и к соблюдению других морально-этических корпоративных принципов. Уже при жизни авторитет и слава Гиппократа были огромны и неоспоримы, а его вклад в медицину не утратил значения до настоящего времени.
«Начала» Евклида
Главный труд Евклида – «Начала» (или «Элементы», в оригинале «Стойхейа»). «Начала» Евклида состоят из 13 книг. Позднее к ним были прибавлены еще две книги.
Первые шесть книг «Начал» посвящены геометрии на плоскости – планиметрии. В философско-теоретическом отношении, в плане философии математики особенно интересна первая книга, которая начинается с определений, постулатов и аксиом, учение о которых было заложено Аристотелем.
Далее, в первой же книге «Начал» Евклида, рассматриваются треугольники, параллельные линии, параллелограммы. Вторая книга «Начал» содержит геометрическую алгебру: числа и отношения чисел выражаются в пространственных величинах и в их пространственных же отношениях. Третья книга «Начал» исследует геометрию круга и окружности, четвертая – многоугольники. Пятая книга дает теорию пропорций как для соизмеримых, так и для несоизмеримых величин. В книге VI Евклид прилагает эти теории к планиметрии. Книги VII – X содержат теорию чисел, причем X книга трактует иррациональные линии. XI, XII и XIII книги «Начал» посвящены стереометрии, при этом в XII книге применяется метод исчерпания.
В строгом смысле слова Евклида нельзя считать «отцом геометрии». Свои «Начала» были у Гиппократа Хиосского в V в. до н. э. В IV в. до н. э. «Начала» были у Леона, и у ФеудияМагнесийского. Метод исчерпания применял ЕвдоксКнидский, возможный учитель Евклида по Академии. Проблемой иррациональности занимались пифагореец ГиппасМетапонтский, Феодор Киренский, Теэтет Афинский. Однако Евклид – не простой передатчик сделанного до него математиками. В «Началах» Евклида мы видим завершение математики как стройной науки, исходящей из определений, постулатов и аксиом и построенной дедуктивно. Математика Евклида – вершина древнегреческой дедуктивной науки. Она резко отличается от ближневосточной математики сее практической приблизительной рецептурностью. Не случайно «Начала» Евклида по их логической стройности, ясности, изяществу и законченности сравнивают с афинским Парфеноном.
Что касается Ближнего Востока, то там Евклид был известен в переводах с греческого на сирийский, а с сирийского – на арабский. Первым арабским философом, который заинтересовался Евклидом, был, по-видимому, аль-Кинди (IX в.). Его интерес ограничивался евклидовой «Оптикой». Однако затем последовала масса переводов и комментариев на «Начала». Эти арабские тексты были переведены в XIII в. на латинский язык. Первый латинский перевод с греческого оригинала был делан в Европе в 1493 г. и отпечатан в 1505 г. в Венеции. Но до 1572 г., когда Федерико Коммандино в своем латинском переводе исправил эту ошибку, Евклида-математика путали с Евклидом Мегариком.
Диофант Александрийский
О подробностях его жизни практически ничего не известно. С одной стороны, Диофант цитирует Гипсикла (II век до н. э.); с другой стороны, о Диофанте пишет Теон Александрийский (около 350 года н. э.), — откуда можно сделать вывод, что его жизнь протекала в границах этого периода. Возможное уточнение времени жизни Диофанта основано на том, что его Арифметика посвящена «достопочтеннейшему Дионисию». Полагают, что этот Дионисий — не кто иной, как епископ Дионисий Александрийский, живший в середине III в. н. э.
В Палатинской антологии содержится эпиграмма-задача:
Прах Диофанта гробница покоит; дивись ей и камень
Мудрым искусством его скажет усопшего век.
Волей богов шестую часть жизни он прожил ребенком.
И половину шестой встретил с пушком на щеках.
Только минула седьмая, с подругой он обручился.
С нею, пять лет проведя, сына дождался мудрец;
Только полжизни отцовской возлюбленный сын его прожил.
Отнят он был у отца ранней могилой своей.
Дважды два года родитель оплакивал тяжкое горе,
Тут и увидел предел жизни печальной своей.
Она эквивалентна решению следующего уравнения:
Это уравнение даёт 
Источник


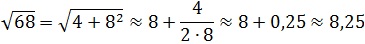
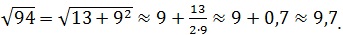
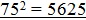
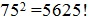







 , т. е. расстояние равно 20 м.
, т. е. расстояние равно 20 м.





















 =
=
 ≈
≈
 ≈5,3
≈5,3























