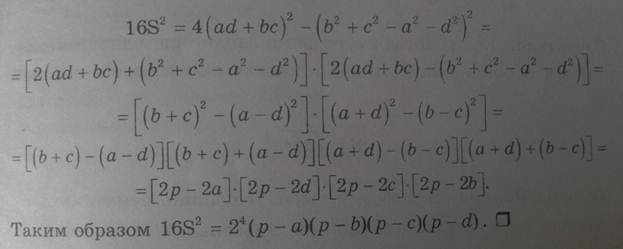Доказательство теоремы эйлера для четырехугольника векторным способом

Четырёхугольник — это геометрическая фигура (многоугольник), состоящая из четырёх точек (вершин), никакие три из которых не лежат на одной прямой, и четырёх отрезков (сторон), попарно соединяющих эти точки. Различают выпуклые и невыпуклые и звездчатые четырёхугольники. Выпуклым четырехугольником называется четырехугольник, у которого все углы меньше развернутого угла. Четырехугольник, у которого угол больше развернутого называется невыпуклым

Виды четырёхугольников

Параллелограмм — четырёхугольник, у которого все противоположные стороны попарно равны и параллельны;
Прямоугольник — четырёхугольник, у которого все углы прямые;
Ромб — четырёхугольник, у которого все стороны равны;
Квадрат — четырёхугольник, у которого все углы прямые и все стороны равны;
Трапеция — четырёхугольник, у которого две противоположные стороны параллельны;
(Дельтоид — четырёхугольник, у которого две пары смежных сторон равны.)

Сумма углов четырёхугольника равна 2 π = 360°.
Четырёхугольник можно вписать в окружность тогда и только тогда, когда сумма противоположных углов равна 180° (). См. также теорема Птолемея.
Четырёхугольник является описанным около окружности тогда и только тогда, когда суммы длин противоположных сторон равны ()
Формула Эйлера: учетверённый квадрат расстояния между серединами диагоналей равен сумме квадратов сторон четырёхугольника минус сумму квадратов его диагоналей.
Средние линии четырёхугольника и отрезок, соединяющий середины его диагоналей, пересекаются в одной точке и делятся ею пополам.
Четыре отрезка, каждый из которых соединяет вершину четырёхугольника с центроидом треугольника, образованного оставшимися тремя вершинами, пересекаются в центроиде четырёхугольника и делятся им в отношении 3:1, считая от вершин.
Две противоположные стороны четырёхугольника перпендикулярны тогда и только тогда, когда сумма квадратов двух других противоположных сторон равна сумме квадратов диагоналей.
Диагонали четырёхугольника перпендикулярны тогда и только тогда, когда суммы квадратов противоположных сторон равны.
Средние линии четырёхугольника равны тогда и только тогда, когда равны суммы квадратов его противоположных сторон.

Теорема Вариньона
Четырёхугольник, вершины которого совпадают с серединами сторон произвольного четырёхугольника, является параллелограммом, стороны которого параллельны диагоналям исходного четырёхугольника.
или сокращённо
Середины сторон произвольного четырёхугольника — вершины параллелограмма
Доказательство
Проведём диагональ AC. Отрезки EF и GH будут средними линиями треугольников и . По теореме о средней линии, отрезки будут параллельны диагонали, а, значит, и друг другу. Повторив аналогичные рассуждения для диагонали BD, получаем, что противоположные стороны четырёхугольника EFGH параллельны, и, по определению, это — параллелограм.
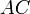
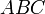
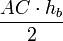
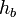
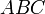
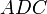
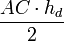
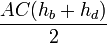
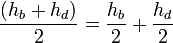
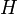
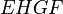
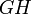
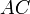
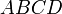
Доказательство, что площадь параллелограмма равна половине площади исходного четырехугольника: Пусть диагональ проходит внутри четырёхугольника. Тогда площадь треугольника равна , где — высота треугольника , проведённая из вершины . Аналогично, площадь треугольника равна . Тогда площадь всего четырёхугольника равна . Но — это сумма расстояний до прямой от точек и , то есть в точности высота параллелограмма . А поскольку сторона параллелограмма вдвое меньше , то и площадь параллелограмма равна половине площади ,

Теорема Эйлера

в любом четырехугольнике сумма квадратов сторон равна сумме квадратов диагоналей, сложенной с учетверенным квадратом расстояния между серединами диагоналями

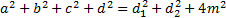
Следствие: Сумма квадратов длин равна диагоналей параллелограмма равна сумме квадратов длин его сторон

Теорема Птолемея
Для любого выпуклого четырёхугольника ABCD вписанного в окружность, сумма произведений длин противоположных сторон равна произведению длин диагоналей AB*DC+BC*AD=BD*AC

Теорема Брахмагупты(площадь вписанного в окружность четырёхугольника)

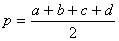
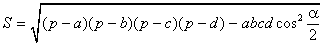
Если a, b, c, d – длины сторон четырёхугольника, – его полупериметр, а α – сумма его противоположных углов, то площадь Sчетырёхугольника равна
.
В качестве α здесь можно взять сумму любой из двух пар противоположных углов, результат от этого не зависит. В случае четырёхугольника, вписанного в окружность, эта формула принимает более простой вид: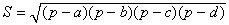
;
это равенство и называется формулой Брахмагупты. Если четырёхугольник имеет и описанную и вписанную окружности, то формула становится совсем короткой: .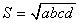

Источник

Урок по теме «Теорема Эйлера»

Урок по теме «Теорема Эйлера»

Целью данных уроков является знакомство учащихся с одним из наиболее важных свойств выпуклых многогранников — теоремой Эйлера. Эта теорема связывает вместе число вершин, ребер и граней выпуклого многогранника. Она положила начало одному из наиболее интенсивно развивающихся в настоящее время направлений геометрии — топологии.

Проверка домашнего задания

Начинаем урок с проверки домашнего задания предыдущего урока, посвященного выпуклым многогранникам и их свойствам. Затем слушаем заранее подготовленное сообщение ученика на тему «Жизнь и творчество JI . Эйлера».

При подготовке этого сообщения можно воспользоваться следующей литературой:

Гиндикин С.Г. Леонард Эйлер//Квант, 1983, № 10 , 11 .

Яковлев А.Я. Леонард Эйлер. —М.: Просвещение, 1983.

Учащимся предлагается заполнить таблицу, поставив в нее числа, соответствующие количеству вершин (В), ребер (Р) и граней (Г) указанных многогранников.

n -угольная пирамида

n -угольная призма

Вопрос. Какая зависимость имеется между числом вершин, ребер и граней этих многогранников?

Ответ. Для всех выбранных многогранников имеет место равенство В — Р + Г = 2.

Оказывается, что данное равенство справедливо не только для указанных многогранников, но и для произвольного выпуклого многогранника. Впервые это свойство выпуклых многогранников было доказано Леонардом Эйлером в 1752 году и получило название теоремы Эйлера.

Теорема Эйлера. Для любого выпуклого многогранника имеет место равенство

где В — число вершин, Р — число ребер и Г — число граней данного многогранника.

Теорему Эйлера историки математики называют первой теоремой топологии — раздела геометрии, который изучает свойства фигур, не меняющихся при непрерывных деформациях, допускающих любые растяжения и сжатия, но без разрывов или дополнительных склеек. Такие свойства называются топологическими. Соотношение Эйлера В — Р + Г = 2 для выпуклых многогранников является как раз таким топологическим свойством. Многогранник можно как угодно деформировать, при этом ребра и грани могут искривляться, однако их число, а следовательно, и соотношение Эйлера не меняются. При этом многогранник может стать невыпуклым, тем не менее для него будет выполняться соотношение Эйлера. Однако есть невыпуклые многогранники, для которых соотношение Эйлера не выполняется. Пример такого многогранника приведен на рисунке 1. Он получается, если в кубе вырезать дыру в форме параллелепипеда.

Учащимся предлагается самостоятельно найти число вершин, ребер и граней этого многогранника.

В результате получаем:

В = 16, Р = 32, Г = 16, В — Р + Г = 0.

Оказывается, что для выполнимости соотношения Эйлера существенным является не столько выпуклость многогранника, сколько то, что у него нет дыр. Поверхность выпуклого многогранника непрерывной деформацией можно сделать такой же, как у шара, а с поверхностью многогранника, изображенного на рисунке 1, этого сделать нельзя.

Доказательство (теоремы Эйлера). Представим поверхность данного многогранника сделанной из эластичного материала. Удалим (вырежем) одну из его граней и оставшуюся поверхность растянем на плоскости.

Это можно сделать, например, с помощью центрального проектирования с центром в точке S , расположенной немного выше удаленной грани ABCDE (рис. 2).

В результате на плоскости получим сетку (рис. 3), состоящую из Г’ = Г — 1 многоугольников (которые по-прежнему будем называть гранями), В вершин и Р ребер.

Для этой сетки нужно доказать равенство

Тогда для многогранника будет справедливо требуемое равенство (*).

Докажем, что соотношение (**) не изменится, если в каком-нибудь многоугольнике сетки провести диагональ. Действительно, после проведения такой диагонали (например, EF ) в сетке будет В вершин, Р + 1 ребер и Г’ + 1 граней, следовательно,

В — (Р + 1) + (Г’ + 1) = В — Р + Г’.

Пользуясь этим свойством, проведем в сетке диагонали, разбивающие входящие в нее многоугольники на треугольники, и для полученной треугольной сетки (рис. 4) покажем выполнимость соотношения (**).

Для этого будем последовательно убирать крайние треугольники. При этом возможны два случая:

а) для удаления треугольника требуется снять одно ребро (на рис. 4 для удаления треугольника ABF требуется снять ребро АВ );

б) для удаления треугольника требуется снять два ребра (на рис. 5 для удаления треугольника BCF требуется снять ребра ВС и BF ).

В обоих случаях соотношение (**) не изменится. Например, в первом случае после удаления треугольника сетка будет состоять из В вершин, Р — 1 ребер и Г’ — 1 граней, В — (Р — 1) + (Г’ — 1) = В — Р + Г’.

Самостоятельно рассмотрите второй случай (рис. 6).

Таким образом, удаление одного треугольника не меняет соотношения (**). Продолжая этот процесс удаления треугольников, в конце концов мы придем к сетке, состоящей из одного треугольника. Для такой сетки В = 3, Р = 3, Г’ = 1, следовательно,

Значит, соотношение (**) имеет место и для исходной сетки, откуда окончательно получаем, что для данного многогранника справедливо соотношение (*).

Задача 1. Гранями выпуклого многогранника являются только треугольники. Сколько у него вершин и граней, если он имеет 12 ребер? Нарисуйте такой многогранник.

Решение. Пусть у данного многогранника будет В вершин, Р ребер и Г граней. Тогда ЗГ = 2Р, где Р = 12, значит, Г = 8. Применяем теорему Эйлера, из которой следует, что В = 2 + Р — Г. В нашем случае В = 2 +12-8 = 6. Итак, В = 6, Р = 12, Г = 8. Примером такого многогранника является октаэдр (рис. 7).

Задача 2. Из каждой вершины выпуклого многогранника выходит три ребра. Сколько он имеет вершин и граней, если число ребер равно 12? Нарисуйте такой многогранник.

Решение. ЗВ = 2Р, учитывая, что Р = 12, имеем: В = 8. По теореме Эйлера

Г=2-В + Р, Г = 2- 8 + 12 = 6.

Таким образом, у данного выпуклого многогранника В = 8, Р=12иГ = 6. Примером такого многогранника является куб.

Задача 3*. Докажите, что в любом выпуклом многограннике число треугольных граней плюс число трехгранных углов больше или равно восьми.

Решение. Обозначим через Г _n число граней с п ребрами. Тогда Г = Г ₃ + + + + . Каждая треугольная грань имеет три ребра, и число треугольных граней равно Г ₃ . Поэтому общее число ребер в треугольных гранях равно З Аналогично, общее число ребер в четырехугольных гранях равно 4 , и т.д.

Поскольку каждое ребро многогранника содержится ровно в двух гранях, то при таком подсчете ребер мы каждое ребро посчитаем дважды, следовательно, будет иметь место равенство

2Р = ЗГ ₃ + + + +… .

Аналогичным образом обозначим через В число вершин, в которых сходится п ребер.

Тогда В = В ₃ + + + В ₆ + .

Значит, для числа ребер (Р) будет иметь место равенство

2Р = + + + +…

Воспользуемся равенством 4В — 4Р + 4Г = 8, получающимся умножением обеих частей равенства Эйлера на 4.

4В = + + + +…

4Г = 4 + 4 + 4 + +…

4Р = 2Р + 2Р = З + 4 , + 5 +

+ +…+ + + + +…

Подставляя эти выражения в указанное равенство, получим:

Из этого следует, что В ₃₊ Г ₃ ≥ 8, что и требовалось доказать.

В качестве приложения теоремы Эйлера рассмотрим задачу Эйлера о трех домиках и трех колодцах.

Задача 4 . Три соседа имеют три общих колодца. Можно ли провести непересекающиеся дорожки от каждого дома к каждому колодцу?

Решение. Попробуем провести требуемые дорожки. На рисунке 8 показано расположение дорожек, две из которых пересекаются. Попытки провести непересекающиеся дорожки к успеху не приводят. Однако это не означает, что этого нельзя сделать. То, что не получается у нас, может получиться у кого-нибудь другого. Если же мы предполагаем, что непересекающиеся дорожки провести нельзя, то это нужно доказать. Доказательство будем вести от противного. Предположим, что это можно сделать. Каждую точку-домик соединим с каждой точкой-колодцем. Получим девять ребер, которые попарно не пересекаются.

Эти ребра образуют на плоскости сетку, аналогичную той, которая была получена при доказательстве теоремы Эйлера. Поэтому для числа вершин, ребер и граней этой сетки должно выполняться соотношение Эйлера В – Р+ Г’ — 1 . Добавим к ней еще одну грань — внешнюю часть плоскости по отношению к исходному многоугольнику. Тогда соотношение Эйлера примет вид В — Р + Г = 2, причем В = 6 и Р = 9. Следовательно, Г должно равняться пяти.

Заметим, что поскольку дорожки не соединяют между собой никакие два домика и никакие два колодца, то у рассматриваемой сетки нет треугольных граней. Каждая из пяти граней имеет по крайней мере четыре ребра. Так как каждое ребро лежит ровно в двух гранях, то количество ребер должно быть не меньше =10, что противоречит тому, что их число равно 9. Полученное противоречие показывает, что ответ в задаче отрицателен — нельзя провести непересекающиеся дорожки от каждого домика к каждому колодцу.

Гранями выпуклого многогранника являются только четырехугольники. Сколько у него вершин и граней, если число ребер равно 12? Нарисуйте такой многогранник.

В каждой вершине выпуклого многогранника сходится по четыре ребра. Сколько он имеет вершин и граней, если число ребер равно 12? Нарисуйте такой многогранник.

Гранями многогранника являются двенадцать правильных пятиугольников, и в каждой вершине сходится три ребра. Сколько у него вершин и ребер? Приведите пример такого многогранника.

4*. Докажите, что у любого выпуклого многогранника найдется треугольная, четырехугольная или пятиугольная грань.

5*. Докажите, что у любого выпуклого многогранника найдется трехгранный, четырехгранный или пятигранный угол.

6. Можно ли четыре домика соединить непересекающимися дорожками с четырьмя колодцами так, чтобы каждый домик был соединен с тремя колодцами и каждый колодец — с тремя домиками?

Ответы и решения

4Г = 2Р, Г = 6, В = 2 + Р — Г, В = 2 + 12 — 6 = 8. Итак, В = 8, Р = 12 и Г = 6. Примером такого многогранника является куб.

4В = 2Р, В = 6, Г = 2 — В + Р, Г = 2 — 6 + 12 = 8. Итак, В = 6, Р = 12, Г = 8. Примером такого многогранника явля ется октаэдр.

ЗВ = 2Р, 5Г = 2Р. Подставляя выражения для В и Г в равенство В — Р + Г = 2, получим: — Р-Р+ Р=2.

Откуда находим Р = 30, В = 20. Примером такого многогранника является додекаэдр.

4*. Имеем равенства: 2Р = ЗВ ₃ + 4В ₄ + 5В ₅ + 6В ₆ + . 2Р = ЗГ ₃ + 4Г ₄ + 5Г ₅ + 6Г ₆ + . Предположим, что у выпуклого многогранника нет треугольных, четырехугольных и пятиугольных граней. Тогда второе равенство можно переписать в виде 2Р = 6Г ₆ + . и из него следует неравенство 2Р ≥ 6Г. Из первого равенства следует неравенство 2Р ≥ ЗВ и, следовательно, неравенство 4Р ≥ 6В. Используя эти неравенства, получим: 6В — 6Р + 6Г ≤ 0. С другой стороны, по теореме Эйлера 6В — 6Р + 6Г = 12. Получили противоречие. Значит, у любого выпуклого многогранника обязательно найдется треугольная, четырехугольная или пятиугольная грань.

5*. Решение аналогично решению задачи 4*.

Попробуем линию, изображенную на рисунке 1, обвести одним росчерком , то есть не отрывая карандаша от листа бумаги и не проходя по одной и той же части линии более одного раза.

Фигура эта, такая простая на вид, оказывается, имеет интересную особенность. Если мы начнем движение из узла В, то у нас это обязательно получится. Один из вариантов обвода показан на рисунке 2.

А что будет, если мы начнем движение из узла А? Легко убедиться, что обвести линию в этом случае нам не удастся: у нас всегда будут оставаться не пройденные отрезки, добраться до которых уже невозможно. Две такие неудачные попытки обхода показаны на рисунках 3 и 4.

Решите задачи 1—5:

а) Удастся ли обвести линию (см. рис. 1), если начать движение из узла С? а из узла D ?

б) Вы начали движение из узла В. Где вы закончите движение?

Назовите все узлы линии (рис. 5), начав с которых ее можно обвести одним росчерком. Начертите в тетради линию одним росчерком, отметьте начало движения и покажите стрелками направление движения.

На рисунке б изображена линия, которую вы, наверное, умеете рисовать одним росчерком. Это звезда. Оказывается, хотя она и выглядит значительно более сложной, чем предыдущие линии, обвести ее можно, начав с любого узла.

Начертите звезду несколько раз, начиная движение из разных узлов.

Линию, изображенную на рисунке 7, как и звезду, можно начертить одним росчерком, начав движение из любого узла. Вычертите эту линию дважды: начав с узла, из которого выходят два отрезка, а затем из узла, из которого выходят четыре отрезка.

а)

б)

Источник