Доказательство как логическая процедура
Полный список ответов по логике
Доказательство — это логическая операция обоснования истинности утверждения с помощью фактов и связанных с ним суждений. С помощью совокупности логических приёмов истинность какого-либо суждения обосновывается исходя из других истинных суждений.
Основу доказательства составляют следующие положения:
Тезис — утверждение, истинность или ложность которого обосновывается посредством данного доказательства
Аргументы и факты — это положения, из которых выводится истинность или ложность тезиса.
Демонстрация (форма доказательства) — способ обоснованной логической связи между утверждаемым тезисом и аргументами
Виды
Доказательства по форме делятся на прямые и (косвенные).
Прямое доказательство идет от рассмотрения аргументов к доказательству утверждаемого тезиса, то есть истинность доказательства непосредственно обосновывается аргументами. Широко используется прямое доказательство в статистических отчетах, в различного рода документах, в постановлениях.
Непрямое (косвенное) доказательство — это доказательство, в котором истинность выдвинутого тезиса обосновывается путём доказательства ложности утверждаемого антитезиса. Оно применяется тогда, когда нет аргументов для прямого доказательства. Антитезис может быть выражен в одной из двух форм:
Если тезис обозначить буквой а , то его отрицание (а) будет антитезисом, то есть противоречащим тезису суждением;
Антитезисом для тезиса а в суждении а. в. с служат суждения в и с .
В зависимости от этого различия в структуре антитезиса косвенные доказательства делятся на два вида – апагогическое (доказательство от «противного») и разделительное доказательство (методом исключения). Первое осуществляется путем установления ложности противоречащего тезису суждения. Этот метод часто используется в математике. Во втором антитезис является одним из членов разделительного суждения, в котором должны быть обязательно перечислены все возможные альтернативы, например: Преступление совершил либо А, либо Б, либо С. Доказано, что не совершали преступление ни А, ни Б. Следовательно преступление совершил С. Истинность тезиса устанавливается путем последовательного доказательства ложности всех членов разделительного суждения кроме одного.
Источник
Доказательство как логическая реальность



Лекция 5
Доказательство – это логическая операция обоснования истинности какого-либо суждения с помощью других истинных и связанных с ним суждений.
Доказательство отличается от других рассуждений, например умозаключений, тем, что его целью является обоснование истинности доказуемого суждения.
В доказательстве выделяют три элемента: 1). Доказываемое положение – тезис; 2). Суждения, с помощью которых обосновывается истинность тезиса, — аргументы, или доводы, или основания доказательства; 3). Логическая связь тезиса с аргументом – демонстрация.
В качестве аргументов в доказательстве могут быть использованы: а). удостоверенные факты; б). законы науки; в). ранее доказанные теоремы; г). аксиомы и постулаты; д). определения.
Для корректного проведения процесса доказательства необходимо учитывать требования, которые предъявляются ко всем элементам доказательства.
Требования к тезису:
— тезис должен нуждаться в доказательстве. Бессмысленно пытаться доказывать очевидные вещи, определения понятий, констатации фактов, аксиомы и постулаты;
— тезис должен быть ясным и четким. Многие слова естественного языка являются многозначными и расплывчатыми, что обусловливает неясность тезиса. Кроме того, следует иметь в виду, что в качестве тезиса лучше брать частные суждения, а не общие. Частное суждение легче доказать и труднее опровергнуть;
— тезис должен оставаться одним и тем же на протяжении всего доказательства. Распространенная ошибка – подмена тезиса. Менее распространенная – потеря тезиса.
Требования к аргументам:
— аргументы должны быть истинными суждениями, причем их истинность должна быть доказана. Нарушение этого требования, связанное с использованием ложного аргумента, называется «предвосхищение основания»;
— истинность аргументов должна устанавливаться автономно, т. е. независимо от тезиса. При нарушении этого требования мы имеем дело с ошибкой, известной как «круг в обосновании» или «круг в доказательстве»;
— совокупность аргументов должна быть непротиворечива. Если аргументы противоречат друг другу, то, по крайней мере, один из них ложен, а ложные документы ничего не доказывают;
-совокупность аргументов должна быть достаточной для вывода тезиса. Один аргумент почти никогда не дает обоснование тезиса, его доказательная сила мала. Но несколько аргументов, находящиеся во взаимной связи, способны создать прочную логическую основу для вывода тезиса. Однако не следует злоупотреблять количеством аргументов. Их должно быть достаточно для вывода тезиса, и не более того. Каждый лишний аргумент ослабляет доказательство. Важно не количество аргументов, а их весомость.
Требования к демонстрации есть не что иное, как требования к умозаключению. Ошибки, связанные с нарушением правил умозаключений, носят общее название «не следует»: тезис логически не вытекает, не следует из аргументов.
Обоснование тезиса в ходе доказательства может осуществляться прямо или косвенно. Исходя из этого различают два вида доказательства.
Прямое доказательство – это обоснование тезиса аргументами без помощи каких-либо дополнительных построений. Цель рассуждений в этом случае начинается с аргументов и с логической необходимостью приводит к признанию истинности тезиса. Другими словами, при прямом доказательстве необходимо найти такие убедительные документы, из которых логически вытекает тезис.
Косвенное доказательство — это обоснование истинности тезиса с помощью антитезиса – суждения, противоречащего тезису. Мы обосновываем ложность антитезиса и, опираясь на закон исключительного третьего, гласящего, что из двух противоположных суждений одно обязательно истинно, тем самым доказываем истинность противоречащего ему утверждения – тезиса. Выделяют два вида косвенного доказательства.
Доказательство от противного основывается на применении закона исключительного третьего. Оно состоит в том, что мы начинаем выводить из антитезиса следствия и показываем, что некоторые из этих следствий (хотя бы одно) противоречат известным истинным положениям (фактам). Таким образом, принятие антитезиса ведет к противоречию (к абсурду), поэтому его следует признать ложным. Но тогда тезис необходимо признать истинным.

Разделительное косвенное доказательство состоит в построении разделительного суждения, элементами которого являются доказываемый тезис и некоторые несовместимые с ним утверждения (антитезисы).затем показывают, что, за исключением тезиса, все элементы разделительного суждения ложны. Следовательно следует признать тезис истинным.
Источник
Способы обоснования истинности суждений
3.7. Способы обоснования истинности суждений
Непременным условием развивающего обучения является формирование у учащихся способности обосновывать (доказывать) те суждения, которые они высказывают. В практике эту способность обычно связывают с умением рассуждать, доказывать свою точку зрения.
Суждения бывают единичными: в них что–то утверждается или отрицается относительно одного предмета. Например: «Число 12 –четное; квадрат АВСD не имеет острых углов; уравнение 23–х = 30 не имеет решения (в рамках начальных классов) и т. д.».
Помимо единичных суждений различают суждения частные и общие. В частных что–то утверждается или отрицается относительно некоторой совокупности предметов из данного класса или относительно некоторого подмножества данного множества предметов. Например: «Уравнение х – 7 = 10 решается на основе взаимосвязи между уменьшаемым, вычитаемым и разностью». В этом суждении речь идет об уравнении частного вида, представляющего собой подмножество множества всех уравнений, изучаемых в начальных классах.
В общих суждениях что–то утверждается или отрицается относительно всех предметов данной совокупности. Например:
«В прямоугольнике противоположные стороны равны». Здесь речь идет о любом, т.е. о всех прямоугольниках. Поэтому суждение является общим, хотя в данном предложении слово «всех» отсутствует. Любое уравнение в начальных классах решается на основе взаимосвязи между результатами и компонентами арифметических действий. Это также общее суждение, так как охватывает всевозможные уравнения, встречающиеся в курсе математики начальных классов.
Предложения, выражающие суждения, могут быть различными по форме: утвердительными, отрицательными, условными (например: «если число оканчивается нулем, то оно делится на 10»).
Как известно, в математике все предложения, за исключением исходных, как правило, доказываются дедуктивно. Суть дедуктивных рассуждений сводится к тому, что на основе некоторого общего суждения о предметах данного класса и некоторого единичного суждения о данном объекте высказывается новое единичное суждение о том же объекте. Общее суждение принято называть общей посылкой, первое единичное суждение – частной посылкой, новое единичное суждение – заключением. Пусть, например, требуется решить уравнение: 7*x=14. Для нахождения неизвестного множителя используется правило: «Если значение произведения разделить на один множитель (известный), то получим другой (значение неизвестного множителя)».
Это правило (общее суждение) – общая посылка. В данном уравнении произведение равно 14, известный множитель 7. Это частная посылка.
Заключение: «нужно 14 разделить на 7, получим 2». Особенность дедуктивных рассуждений в начальных классах заключается в том, что они применяются в неявном виде, т. е. общая и частные посылки в большинстве случаев опускаются (не проговариваются), ученики сразу приступают к действию, которое соответствует заключению.
Поэтому, собственно, и создается впечатление, что дедуктивные рассуждения отсутствуют в курсе математики начальных классов.
Для сознательного выполнения дедуктивных умозаключений необходима большая подготовительная работа, направленная на усвоение вывода, закономерности, свойства в общем виде, связанная с развитием математической речи учащихся. Например, довольно длительная работа по усвоению принципа построения натурального ряда чисел позволяет учащимся овладеть правилом:
«Если к любому числу прибавить 1, то получим следующее за ним число; если из любого числа вычтем 1, то получим предшествующее ему число».
Составляя таблицы П+1 и П – 1, ученик фактически пользуется этим правилом как общей посылкой, выполняя тем самым дедуктивные рассуждения. Примером дедуктивных умозаключений в начальном обучении математике является и такое рассуждение:
«4 или =, чтобы получилась верная запись:
учащиеся предпочитают заменять рассуждения вычислениями:
125–87 . 127–87 246–93 . 249–93 584–121. 588– 121
4. Сравни выражения и поставь знаки или = :
304:8 . 3044 243:9 . 243:3 1088:4 . . 1088:2
5. Как быстро найти сумму в каждом столбике:
9999 12 15 12 16 30 30 32 32 40 40 40 40 Ответ: 91.
Таким образом, дедуктивные рассуждения могут являться одним из способов обоснования истинности суждений в начальном Курсе математики. Учитывая, что они доступны не всем младшим школьникам, в начальных классах используются и другие способы обоснования истинности суждений, которые в строгом смысле нельзя отнести к доказательствам. К ним относятся эксперимент, вычисления и измерения.
Эксперимент обычно связан с применением наглядности и предметных действий. Например, ребенок может обосновать суждение 7 > 6, выложив в одном ряду 7 кругов, под ним – 6. Установив между кругами первого и второго ряда взаимно–однозначное соответствие, он фактически обосновывает свое суждение (в первом ряду один круг без пары, «лишний», значит, 7>6). Ребенок может обращаться к предметным действиям и для обоснования истинности полученного результата при сложении, вычитании, умножении и делении, при ответе на вопросы: «На сколько одно число больше (меньше) другого?», «Во сколько раз одно число больше (меньше) другого?». Предметные действия могут быть заменены графическими рисунками и чертежами. Например, для обоснования результата деления 7:3=2 (ост.1) он может использовать рисунок:
Для формирования у учащихся умения обосновывать свои суждения полезно предлагать им задания на выбор способа действия (при этом оба способа могут быть: а) верными, б) неверными, в) один верным, другой неверным). В этом случае каждый предложенный способ выполнения задания можно рассматривать как суждение, для обоснования которого учащиеся должны использовать различные способы доказательств.
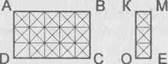
Например, при изучении темы «Единицы площади» учащимся предлагается задание (М2И):
Во сколько раз площадь прямоугольника АВСD больше прямоугольника КМЕО? Запиши ответ числовым равенством.
Маша записала такие равенства: 15:3=5, 30:6=5.
Миша – такое равенство: 60:12=5.
Кто из них прав? Как рассуждали Миша и Маша?
Для обоснования суждений, высказанных Мишей и Машей, учащиеся могут использовать как способ дедуктивных рассуждений, где в качестве общей посылки выступает правило кратного сравнения чисел, так и практический. В этом случае они опираются на приведенный рисунок.
Предлагая способ решения задачи, учащиеся также высказывают суждения, используя для их доказательства математическое содержание, данное в сюжете задачи. Прием выбора готовых суждений активизирует эту деятельность. В качестве примера можно привести такие задания:
Туристы в первый день прошли 18 км, во второй день, двигаясь с той же скоростью, они прошли 27 км. С какой скоростью шли туристы, если они затратили на весь путь 9 ч?
Миша записал решение задачи так:
3) 2+3=5 (км/ч) Маша – так:
2) 45:9=5 (км/ч) Кто из них прав: Миша или Маша?
Сколько картофелин собрали с 10 кустов, если с трех собрали по 7 картофелин, с четырех по 9, с шести по 8, а с семи по 4 картофелины? Маша решила задачу так:
3) 21+28=49 (к.) Ответ: 49 картофелин собрали с 10 кустов. А Миша так решил задачу:
3) 36+48=84 (к.) Ответ: 84 картофелины собрали с 10 кустов. Кто из них прав?
Процесс выполнения любого задания должен всегда представлять цепочку суждений (общих, частных, единичных), для обоснования истинности которых учащиеся используют различные способы.
Покажем это на примере заданий:
V Вставь числа в «окошки», чтобы получились верные равенства:
П : 6 = 27054 П:7= 4083 (ост. 4)
Учащиеся высказывают общее суждение: «если значение частного умножим на делитель, то получим делимое». Частное суждение: «значение частного – 27054, делитель – б». Заключение:
Теперь в качестве общей посылки выступает алгоритм письменного умножения, находится результат: 162324. Высказывается суждение: 162324:6=27054.
Истинность этого суждения можно проверить, выполнив деление «уголком» или воспользовавшись калькулятором.
Аналогично поступают со второй записью.
Составь верные равенства, используя числа: 6, 7, 8, 48, 56.
Учащиеся высказывают суждение:
6*8=48 (обоснование – вычисления) 56 – 48=8 (обоснование – вычисления)
8*6=48 (для обоснования суждения можно воспользоваться общей посылкой: «от перестановки множителей значение произведения не изменится»).
48:8=6 (тоже возможна общая посылка и т.д.)’ Таким образом, в большинстве случаев для обоснования истинности суждений в начальном курсе математики учащиеся обращаются к вычислениям и дедуктивным рассуждениям. Так, обосновывая результат при решении примера на порядок действия, они пользуются общей посылкой в виде правила порядка действий, затем выполняют вычисления.
Измерение как способ обоснования истинности суждений обычно применяется при изучении величин и геометрического материала. Например, суждения: «синий отрезок длиннее красного», «стороны четырехугольника равны», «одна сторона прямоугольника больше другой» дети могут обосновать измерением.
• Задание 93. Опишите способы обоснований истинности суждений. высказанных учащимися при выполнении следующих заданий. При изучении каких вопросов курса математики начальных классов целесообразно предложить эти задания 9
Можно ли, не выполняя вычислений, утверждать, что значения выражений в каждом столбике одинаковы:
9*7+9+5 8*6+8+3 7*9+9+5 8*7+3 9*8+5 7*8+3
Можно ли утверждать, что значения выражений в каждом столбике ‘одинаковы:
12*5 16*4 (8+4)*5 (8+8)*4 (7+5)*5 (9+7)*4 (10+2)*5 (10+6)*4
Вставь знаки или =, чтобы получились верные записи:
(14+8)*3 . 14*3+8*3 (27+8)*6 . 27*6+8 (36+4)*18 . 40*18 .
Какие знаки действий нужно вставить в «окошки», чтобы получить верные равенства
8*8=8П7П8 8*3=8П4П8 8*6=6П8П0 8*5=8П0П32
Можно ли утверждать, что значения выражений в каждом столбике одинаковы:
8*(4*6) (9*3)*3 8*24 2*27 (8*4)*6 9*(3*2) 6*32 (2*3)*9
Источник