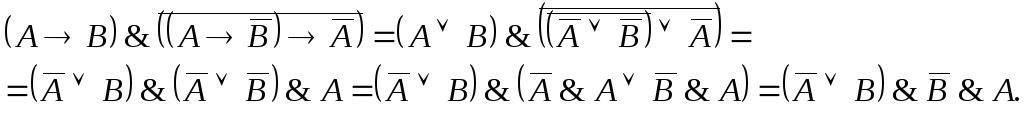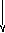Доказать тождественную истинность формулы двумя способами

Совершенная нормальная форма — дизъюнктивная и конъюнктивная, правило построения

Что такое СДНФ

Нормальная форма логической формулы характеризуется тем, что для нее не свойственны эквивалентность, отрицание формул неэлементарного типа и знаки импликации.

Существует две формы нормального типа: КНФ (конъюнктивная нормальная форма) и ДНФ (дизъюнктивная нормальная форма).

СДНФ — совершенная дизъюнктивная нормальная форма формулы. СДНФ — способ написания функции алгебры логики в качестве логического выражения.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

СДНФ формулы — это равнозначная ей формула, которая представляет собой дизъюнкцию элементарных конъюнкций, при которых функция достигает показателя «1».

ДНФ выглядит следующим образом:

СДНФ обладает некоторыми определенными свойствами:

• включает различные элементарные конъюнкции;
• все логические слагаемые формулы содержат все переменные, которые входят в функцию F;
• ни в одном логическом слагаемом не содержится переменная и её отрицание.

К СДНФ возможно привести любую формулу алгебры логики. Исключение составляет только тождественно ложная формула. СДНФ можно получить как используя таблицы истинности, так и через равносильные преобразования.

При построении таблицы истинности важно помнить, что логические переменные со значением «0» необходимо брать с отрицанием.

Что такое СКНФ

СКНФ — совершенная конъюнктивная нормальная форма. Формулу можно назвать таковой, когда она — конъюнкция неповторяющихся элементарных дизъюнкций.

Формула должна соответствовать нескольким условиям, чтобы называться СКНФ:

• в ней отсутствуют одинаковые элементарные дизъюнкции;
• дизъюнкции не содержат одинаковые переменные;
• все дизъюнкции содержат каждую переменную из входящих в конъюнктивную нормальную функцию такого типа.

Правила построения по таблице истинности

Дизъюнктивная форма

Если функция равна 1, то для всех наборов переменных, при которых это происходит, записывается произведение. Однако переменные, которые имеют значение 0, берутся с отрицанием.

Конъюнктивная форма

Когда функция равна 0, то для всех наборов переменных, при которых это происходит, записывается сумма. Однако переменные, которые имеют значение 1, берутся с отрицанием.

Алгоритм приведения к СДНФ и СКНФ

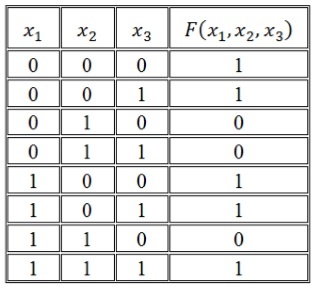
Рассмотрим логическую функцию в виде таблицы истинности.

Алгоритм построения СДНФ по таблице истинности выглядит следующим образом:

1. Отметить наборы переменных, значение функции F на которых равно 1.
2. Записать для всех отмеченных наборов конъюнкцию всех переменных так: если значение некоторой переменной в этом наборе равняется 1, в конъюнкцию включается сама переменная. В случае противного результата, в конъюнкцию включается ее отрицание.
3. Связать полученные конъюнкции операциями дизъюнкции.

Построим совершенную ДНФ:

И как результат получим следующую СДНФ:

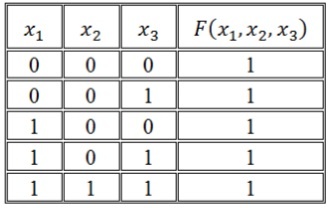
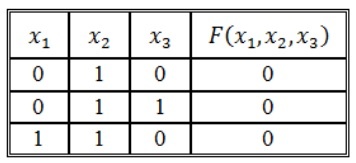
Алгоритм построения СКНФ по таблице истинности выглядит следующим образом:

1. Отметить в таблице истинности наборы переменных, значение функции F на которых равно 0.
2. Записать для всех отмеченных наборов дизъюнкцию всех переменных — в том случае, когда значение некоторой переменной в этом наборе равняется 0, в дизъюнкцию включается сама переменная, если происходит наоборот, то в дизъюнкцию включается ее отрицание.
3. Связать полученные дизъюнкции операциями конъюнкции.

Построим совершенную КНФ:

И как результат получим следующую СКНФ:

Рассмотрев алгоритмы построения СДНФ и СКНФ ясно, что в случае подавляющей части наборов значений переменных функция равна 0, то значительно легче построить и СДНФ для получения ее формулы, а в обратном случае — СКНФ.

Доказательство эквивалентности

Эквивалентность — понятие, означающее, что две и более формул представляют одну и ту же функцию. Для обозначения эквивалентности могут использоваться следующие знаки: \( \equiv , = , \Leftrightarrow .\)

Доказать эквивалентность формул можно двумя способами.

1. Первый заключается в построении и сравнении таблиц истинности обеих функций. В этом случае результат будет истинным только в том случае, когда оба высказывания либо ложны, либо истинны.
2. Второй вариант — метод эквивалентных преобразований. Суть этого метода — построение цепи эквивалентных формул на основе ранее доказанных эквивалентностей.

Далее следуют примеры с некоторыми эквивалентными преобразованием в булевой алгебре и новыми эквивалентностями, которые возможно получить с их помощью.

Поглощение

Склеивание

Обобщенное склеивание

\(xz\;\vee\;y\overline z\;\vee\;xy\;=\;xz\;\vee y\overline z\)

\(xz\;\vee\;y\overline z\;\vee\;xy\;=\;xz\;\vee y\overline z\;\vee\;xyz\;\vee\;xy\overline z\;=\;xz\;\vee\;y\overline z\)

Расщепление

\(x\;\vee\;\overline xy\;=\;xy\;\vee\;x\overline y\;\vee\;\overline xy\;=\;xy\;\vee\;x\overline y\;\vee\;xy\;\vee\;\overline xy\;=\;x\;\cdot\;l\;\;\vee\;y\;\cdot\;l\;=\;x\;\vee\;y\)

Примеры с решением

Задача №1

Приведите к СКНФ \(((((A\rightarrow B)\rightarrow\overline A)\rightarrow\overline B)\rightarrow\overline C)\) .

Через применение закона де Моргана и правила \( x\;\rightarrow\;y\;=\;\overline x\;\vee\;y\) упростим выражения:

\(F\;=\;((((A\;\rightarrow\;B)\;\rightarrow\;\overline A)\;\rightarrow\overline B)\;\rightarrow\;\overline C)\;=\;(((\overline A\;\vee\;B)\;\rightarrow\;\overline A)\;\rightarrow\;\overline B)\;\rightarrow\overline C\;)\;=\)

\(=\;((((\overline A\;\vee\;B)\;\rightarrow\overline A)\;\rightarrow\overline B)\;\rightarrow\;\overline C)\;=\;((\overline<((\overline A\;\vee\;B)>\;\vee\;\overline A)\;\rightarrow\overline B)\;\rightarrow\overline C)\;=\)

\(=(((\overline A\;\vee\;B)\;\vee\;\overline A)\;\rightarrow\;\overline B)\;\rightarrow\;\overline C)\;=((\overline<(\overline<(\overline A\vee B)>\;\vee\;\overline A\;)>\;\vee\;\overline B)\;\rightarrow\;\overline C)\;=\)

\(=\;((\overline<(\overline A\;\vee\;B)>\;\vee\;\overline A)\;\wedge\;B)\;\vee\;\overline C\;=\;(((A\;\wedge\;\overline B)\;\vee\;\overline A)\;\wedge B)\;\vee\;\overline C\;=\)

\(=((A\overline B\;\vee\;\overline A)\;\vee\;\overline A)\;\wedge\;B)\;\vee\;\overline C\;=(((A\;\wedge\;\overline B)\;\vee\;\overline A)\;\wedge\;B)\;\vee\;\overline C\;=\)

\(=\;((A\overline B\;\vee\;\overline A)\;\wedge\;B)\;\vee\;\overline C\;=\;(A\overline BB\;\vee\;\overline AB)\;\vee\;\overline C\;=\;(0\;\vee\;\overline AB)\;\vee\;\overline C\;=\;\overline AB\;\vee\;\overline C\)

Далее приведем выражение к КНФ:

\(F\;=\;\overline AB\;\vee\;\overline C\;\;=\;(\overline A\;\vee\;\overline C)\;\wedge\;(B\;\vee\;\overline C)\)

Далее приведем выражение к СКНФ:

\(F\;=\;(\overline A\;\vee\;\overline C)\;\wedge\;(B\;\vee\;\overline C)\;=\;(\overline A\;\vee\:\overline C\;\vee\;B\overline B)\;\wedge\;(A\overline A\;\vee\;B\;v\;\overline C)\;=\)

\(=\;(\overline A\;\vee\;\overline C\;\vee\;B)\;\wedge\;(A\;\vee\;B\;\vee\;\overline C)\;\wedge\;(\overline A\;\vee\;\overline C\;\vee\;\overline B)\;\wedge\;(\overline A\;\vee\;B\;\;\overline C)\)

Задача №2

Используя эквивалентные преобразования, постройте ДНФ функции \(f(\widetilde x^n)\)

\(f(\widetilde x^3) = (\overlinex_2\;\oplus\;x_3)\;\cdot\;(x_1x_3\;\rightarrow\;x_2)\)

\(f(\widetilde x^3) = (\overlinex_2\;\oplus\;x_3)\;\cdot\;(x_1x_3\;\rightarrow\;x_2) = ((\overlinex_2\;\cdot\;\overline\;)\;\vee\;(\overline<\overlinex_2>\;\cdot\;x_3))\;\cdot\;(\overline\;\vee\;x_2)\;=\)

\(=(\overlinex_2\overline\;\cdot(x_1\vee x_3\vee x_2)\;\vee\;x_1x_3\;\cdot\;(\overline\;\vee\;\overline\;\vee\;x_2)\;\vee\;\overlinex_3\;\cdot\;(\overline\;\vee\;\overline\;\vee\;x_2))\;=\)

Источник

Практическое занятие 1 «Логика высказываний и предикатов»

1. Теоретические вопросы

Понятие высказывания. Атомы. Логические связки.

Формулы логики высказываний. Высказывательные формы.

Интерпретация формул логики высказываний. Общезначимые, противоречивые и выполнимые формулы логики высказываний.

4. Логические функции и формулы логики высказываний.

5. Аксиомы и основные тождества логики высказываний (с доказательством).

6. Нормальные формы формул логики высказываний.

7.Алгоритмы приведения формул к СДНФ и СКНФ.

8. Логические следствия. Теоремы о логических следствиях. Понятие теоремы в логике высказываний.

Определение n-местного предиката. Предметная область и множество истинности предиката..

Определение равносильности предикатов. Тождественно истинные и тождественно ложные предикаты.

Алфавит языка предикатов. Кванторы всеобщности и существования.

Понятие “терма” и формулы логики предикатов.

Интерпретация формул в логике предикатов.

Интерпретация формул логики предикатов, заданных в различной форме.

Общезначимые, противоречивые и выполнимые формулы логики предикатов.

Понятие исчисления предикатов. Полуразрешимость исчисления предикатов. Теорема Эрбрана.

Аксиомы логики предикатов (с доказательством).

Аксиомы переноса квантора через отрицание.

Вынос квантора за скобки.

Переименование связанных переменных в формулах логики предикатов.

Приведенные и предваренные нормальные формы формул логики предикатов.

Алгоритм получения предваренной нормальной формы формул логики предикатов.

Сколемовские стандартные формы формул логики предикатов.

Алгоритм элимирования кванторов существования в формулах логики предикатов.

Множество дизъюнктов формы Сколема.

Резолютивный вывод в исчислении высказываний. Понятие резолюции и резольвенты.

Исчисление высказываний с помощью метода резолюций.

Понятие подстановки и унификации в методе резолюций исчисления предикатов.

Понятие наибольшего общего унификатора для множества дизъюнктов.

Алгоритм унификации в методе резолюций исчисления предикатов. Теорема унификации.

Метод резолюций для логики предикатов первого порядка.

2. Примеры решения типовых задач

Задача 1.Доказать выполнимость формулы логики высказываний:

.

Решение.Формула называется выполнимой, если существует хотя бы один такой набор значений истинности простейших элементарных высказываний (символов), при которых эта формула принимает значение И (истина).

Самый простой метод решения задачи – построить таблицу истинности данной формулы. В этом случае формула интерпретируются как логическая функция f(Q, P, R), определенная на множестве <И, Л>, со значениями в этом же множестве,полученная с помощью логических операций: инверсии (), конъюнкции (& ), дизъюнкции () и импликации ().

PR

Как следует из табл.1, функция f(Q,P,R) принимает значение И на трех наборах , , . Следовательно, эта функция выполнима.

По другому к этому же выводу можно прийти, приведя исходную формулу к СДНФ:

Kаждый из трех конъюнктов принимает значение И на одном из трех наборов , , .

Задача 2.Доказать тождественную истинность формулы:

.

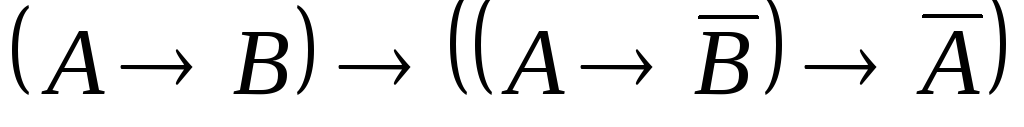
Решение.Приведем решение задачи тремя способами: построение таблицы истинности (таблица 2), использование аксиом логики высказываний и с помощью метода резолюций.

Таблица истинности будет иметь вид:

Из табл.2 следует, что формула истинна на всех наборах A и B.

Выполним преобразования исходной формулы, используя аксиомы логики высказываний.

Формула тождественно истинна.

Для доказательства общезначимости исходной формулы необходимо опровергнуть (доказать тождественную ложность) следующее выражение:

, ( * )

приведя его предварительно к конъюнктивной нормальной форме:

Строим семантическое дерево вывода:

A— исходные дизъюнкты

R₁=— резольвента первого уровня

R₂=— резольвента второго уровня-пустой дизъюнкт

Вывод пустого дизъюнкта есть доказательство невыполнимости формулы (*) или общезначимости исходной формулы.

Задача 3. Доказать эквивалантность формулы:

Решение. Доказательство эквивалентности левой и правой частей формулы можно провести или построением таблицы истинности, или преобразованием левой части.

Используем второй путь.

Задача 4.Записать на языке логики предикатов следующие высказывания: а) любое рациональное число является действительным числом; б) некоторые действительные числа являются рациональными; в) определение непрерывной функцииf:в точке(R-множество действительных чисел).

Решение. Перефразируем высказывание а) следующим образом: “ для любого x: еслиx рациональное число, тоxесть действительное число”.

Введем следующие значения предикатов:

Тогда высказывание а) запишется в виде формулы:

F:

Высказывание б) переформулируем так: “ существуют такие x, чтоxявляется действительным числом ”. На языке логики предикатов это запишется так:

И, наконец, запишем определение непрерывности в точке: “ функция действительного переменного называется непрерывной в точке, если для любого сколь угодно малого положительного числаE>0 найдется такое положительное число>0, что если || ¢ .ØA(x) (допущение)

10 ¢ A(x) («- удаление,8)

11 ¢ .Ø»xA(x) (слабое удалениеØ)

14. $xØA(x)®Ø»xA(x) (теорема дедукции,7,12)

15. Ø «x A(x) « $x Ø A(x)(« — введение, 6,13).

2) «x (P(x)®Q(x)) |- «x P(x)® «x Q(x) :

Формула вида Q₁x₁…Q_nx_nA, гдеAбескванторная формула, аQ_iесть»или$, называется предваренной (или пренексной)нормальной формой.

ТЕОРЕМА 9.У всякой формулы исчисления предикатов есть эквивалентная ей предваренная нормальная форма.

ТЕОРЕМА (Геделя о полноте исчисления предикатов).|-EÛ|=E.

Следствие.Исчисление предикатов непротиворечиво.

1. Обосновать допустимость производных правил вывода исчисления предикатов.

2.Доказать следующую теорему: Какова бы ни была формула Eи нуль-местная предикатная букваP, всегда|-E

(P&F₁)Ú(ØP&F₂), гдеF_iестьPилиØP, или некоторая формула, не содержащаяP(i=1,2).

3. Доказать основные тавтологии исчисления предикатов с кванторами.

4. Найти ошибку в выводе:

P(x), $x Q(x) ú- $x(Q(x) & P(x))

$x P(x), $x Q(x) ú- $x(Q(x) & P(x))

$x P(x) & $x Q(x) ú- $x(Q(x) & P(x))

ú-$x P(x) & $x Q(x) ®$x(Q(x) & P(x))

5. Доказать, что следующие теоремы имеют место, если A(x,x) является результатом подстановки ‘x’ вместо свободных вхождений ‘y’ вA(x,y), причем ‘x’ свободно для ‘y’ вA(x,y) :

«x»y A(x,y)®»x A(x,x) b)$x A(x,x)®$x$y A(x,y)

6. Какое из утверждений верно: A(x)ú-«xA(x) илиú-A(x)Þ»xA(x)?

7. Доказать теорему 9.

8. Привести к предваренной форме формулу:

(Ø$x P(x)Ú»x Q(x)) & (R®»x S(x))

9. Являются ли выводимыми следующие формулы:

(«xP(x)®P(y))®(«xP(x)®»yP(y)), гдеP– одноместная предикатная буква;

10. Доказать при условии, что переменная xне входит свободно в формулы списка Г : (a) Если Гú-A(x)

Обосновать правильность вывода: «x(P(x)

P(x) Ú «x $y (P(x) ® Q(y))

P(x) Ú «x$y($z R(x,w,z) ® Q(y)).

12. Доказать УТВЕРЖДЕНИЕ об эквивалентности конгруентных формул.

13. Доказать, что если множества формул T₀,T_1,T_2,… непротиворечивы иT_iÍT_i+1(i=0,1,…), то È T_i — непротиворечивое множество формул.

14. Пусть множество Г È <$xA(x)>непротиворечиво. Доказать, что если переменная ‘y’ не входит в Г и$xA(x), то множество ГÈ <$xA(x),A(y)>непротиворечиво.

15. Пусть множество формул Г полно и непротиворечиво. Доказать, что для любых замкнутых (не содержащих свободных переменных) формул AиBверно:a) Г|-A&BÛГ|-Aи Г|-B;

b) Г|-AÚBÛГ|-Aили Г|-B;

d) Г|-A®BÛне(Г|-A) или Г|-B.

16. Добавим в алфавит исчисления предикатов функциональные символы f ( n ) (x₁,…,x_n) (n³0) и определим новые выражения – термы: (1)x₁,x₂,…-термы; (2) еслиt₁,…,t_n– термы иf ( n ) (x₁,…,x_n) (n³0) – функциональный символ, тоf ( n ) (t₁,…,t_n) — функциональный терм.

Интерпретациями функциональных символов являются отображения (соответствующей местности) на заданной предметной области D¹Æ.

Найти значения функционального терма t=f(f(x)) на областиD=

и построить истинностную таблицу формулы P(f(x))®$xØP(f(f(x))).

17. Какие из термов: (a)f(x,y), (b)g(w,y), (c)g(z,f(x,y)), (d)g(y,f(h,x))

свободны для ‘x’ в формуле ‘»w(P(x,y)Ú$zQ(y,z)®R(w))’?

18. Пусть x– произвольная переменная иA(x) – произвольная формула,

t– терм, свободный дляxв формулеA(x).Доказать, что

19. Пусть формулы Г не содержат свободно переменной xи термtсвободен дляxв формулеA(x). Доказать, что Г|-A(x)ÞГ|-A(t).

Практическое занятие 2

Задание 1. Компоненты сильной связности ориентированного графа.

С помощью матрицы смежности найти компоненты сильной связности ориентированного графа D.

Cоставляем матрицу смежности A(D) размерности (n− количество вершин) для данного ориентированного графа: она состоит из нулей и единиц, номера строк – индексы вершин , из которых исходят дуги, номера столбцов – индексы вершин, в которые дуги входят (если есть дуга, исходящая из вершины v_i и входящая в v_j, то элемент матрицы смежности, стоящий на пересечении i-той строки и j-того столбца равен 1, иначе – 0.).

Для того, чтобы выделить компоненты сильной связности, необходимо сначала найти матрицу достижимости T(D) ориентированного графа по первой формуле утверждения 3, затем находим матрицу сильной связности S(D) ориентированного графа (она должна быть симметрической) по второй формуле из того же утверждения.

Источник