Способы развертки
Развертки можно разделить на детерминированные, при которых траектория движения развертывающего элемента четко определена и наперед задана, и недетерминированные, в которых направление движения развертывающего элемента автоматически устанавливается в зависимости от, содержания изображения. Последние возникли в связи с потребностью в оптимизации передачи и обработки визуальной информации.
Детерминированные развертки
Можно сформировать много различных траекторий движения развертывающего элемента при разложении изображения. Лучшей следует считать такую, которая обеспечивает разложение при удовлетворении следующих условий:
За полный цикл развертки передаются все элементы разложения, причем каждый однократно и за одно и то же время.
Частота кадров наименьшая.
Непроизводительные потери времени (на обратный ход развертки) минимальные.
Простота технической реализации. Первому условию удовлетворяют все линейные развертки (рис. 2.10): построчная (а), образуемая перемещением с постоянной скоростью развертывающего элемента вдоль параллельных линий (строк), смещающихся на один шаг, построчно-реверсивная (б), у которой направление смещения строк от кадра к кадру меняется на обратное; чересстрочные, при которых строчки прочерчиваются не подряд, а через одну (в), через две (д) и более, разделяя кадр соответственно на 2, 3 и более полей. Этому условию удовлетворяет и чересточечная развертка (г), в которой осуществляется чересстрочное разложение по вертикали и через элементное — вдоль строки: сначала передаются все белые на рисунке элементы в нечетных строках, затем в четных, после этого все синие элементы в нечетных строках, а затем в четных — весь кадр передается за четыре поля.
При реализации рассмотренных разверток оптико-механическими устройствами (например, с помощью диска Нипкова) они удовлетворяют и условию 3. Однако в электронных системах из-за того, что луч с конца одной строки должен вернуться в начало следующей и с конца одного кадра в начало следующего (кроме построчно-реверсивной развертки (б)), потери на обратный ход неизбежны и, следовательно, условие 3 не выполняется. Условию 2 хуже всего удовлетворяет построчно-реверсивная развертка, так как она приводит к снижению повторения крайних строк по сравнению с построчной (а) разверткой и в результате к необходимости повышения частоты кадров п. Лучше всего этому условию удовлетворяет чересточечная развертка (г), но она не удовлетворяет условию 4. Компромиссным вариантом, удовлетворяющим условиям 2 и 4, является чересстрочная развертка ◊, позволяющая снизить число кадров , воспроизводимых в секунду, в два раза по сравнению с построчной разверткой. Дальнейшее уменьшение частоты кадров за счет повышения коэффициента чересстрочности не удается, так как возникают межстрочные мерцания, поскольку угловое расстояние между строчками одного поля становится больше γ0
Здесь и в дальнейшем, если не указана кратность чересстрочной развертки, подразумевается, что она равна двум.
Зигзагообразные развертки (е, ж) удовлетворяют условию 3, но не удовлетворяют остальным: неизбежны пропуски и повторения элементов на краях растра, что противоречит условию 1, сложно осуществить идентичность прямых и обратных ходов, что противоречит условию 4.
Синусоидальная развертка (3) удовлетворяет условиям 3 и 4, но не удовлетворяет 1 и 2. Поэтому она применяется там, где требования к простоте аппаратуры являются первостепенными.
Спиральная развертка (и) с постоянной угловой скоростью достаточно хорошо удовлетворяет всем условиям, кроме 1. При переменной угловой скорости она может удовлетворить требованию 1, но тогда не будет удовлетворять 4.
Сопоставление различных траекторий разверток показывает, что наиболее целесообразной для систем телевизионного вещания, а также для ряда других систем, где ставится задача получения изображения обычных объектов, является чересстрочная развертка. Этот вид развертки в настоящее время наиболее распространен. Телевизионное вещание во всем мире работает по системе чересстрочной развертки.
Недостатки чересстрочной развертки проявляются при передаче движущихся изображений, контуры которых воспроизводятся размытыми . Рассмотрим, например, как будет воспроизводиться вертикальная полоса (рис. 2.11, а) шириной в 3/50 длины строки, движущаяся в направлении строчной развертки с такой скоростью u 1 что за 1 с она перемещается на ширину кадра. За время передачи одного поля (1/50 с) она сдвинется на 1/3 своей ширины и вследствие этого после развертки второго поля воспроизведется изломанной (рис. 2.11, б).
При передаче изображений, движущихся в вертикальном направлении, также происходит потеря четкости. Пусть передается изображение, перемещающееся в направлении кадровой развертки с такой скоростью u 2 что за время одного поля оно смещается вниз на одну строку (рис. 2.11, в). Рассмотрим, как будут воспроизводиться находящиеся на этом изображении две темные точки а и в, расположенные в соседних строках, каждая размером в один элемент разложения. Допустим, что при передаче первого поля точка б попадает на строку, а точка а — между строк, следовательно, в первом поле точка б будет воспроизведена, а точка а пропущена. При передаче второго поля (рис. 2.11, г) изображение сместится вниз на одну строку и, следовательно, точка б будет воспроизведена повторно на соседней строке, а точка а снова пропущена. После развертки полного кадра изображение точки а не воспроизведется, а точки б удлинится в два раза (рис. 2.11, д). Поэтому в устройствах, предназначенных для визуального анализа относительно быстро перемещающихся объектов, предпочтительнее построчная развертка. Спиральная развертка, несмотря на недостатки, может найти применение в специализированных устройствах, где другие виды разверток неприменимы. Допустим, что нужно передать изображение объекта, вращающегося со скоростью v об /с вокруг своей оси (рис. 2.12). Очевидно, и изображение объекта на мишени датчика сигнала будет вращаться с такой же скоростью.
Если обычным способом передать это изображение, то на экране приемника оно тоже будет вращаться, поэтому рассмотреть его невозможно. Применение спиральной развертки, центр которой совпадает с осью вращения объекта, позволяет видеть изображение объекта на экране приемника неподвижным, если скорость развертки в передающем устройстве сделать больше, чем в приемном, так, чтобы развертка догоняла убегающее изображение. Это условие будет выполнено, если в передающем устройстве скорость развертки составляет n+v кадров в секунду, а в приемном — п кадров в секунду.
Источник
Развертка поверхности. Способы построения разверток
Цель лекции: изучение свойств развертки и способов построения разверток многогранников и поверхностей вращения
· Развертка поверхностей. Общие понятия.
· Способы построения разверток: методы триангуляции, нормального сечения и раскатки.
· Построение разверток гранных поверхностей и поверхностей вращения.
Развертка поверхностей. Общие понятия
| Развертка | плоская фигура, полученная при совмещении поверхности геометрического тела с плоскостью (без наложения граней или иных элементов поверхности друг на друга). Развертку можно рассматривать как гибкую, нерастяжимую пленку. Некоторые из представленных таким образом поверхностей можно путем изгибания совместить с плоскостью. При этом, если отсек поверхности может быть совмещен с плоскостью без разрывов и склеивания, то такую поверхность называют развертывающейся, а полученную плоскую фигуру – ее разверткой. |
| Основные свойства развертки | 1 Длины двух соответствующих линий поверхности и ее развертки равны между собой; 2 Угол между линиями на поверхности равен углу между соответствующими им линиями на развертке; 3 Прямой на поверхности соответствует также прямая на развертке; 4 Параллельным прямым на поверхности соответствуют также параллельные прямые на развертке; 5 Если линии, принадлежащей поверхности и соединяющей две точки поверхности, соответствует прямая на развертке, то эта линия является геодезической. |
Методы триангуляции, нормального сечения и раскатки
Построение разверток гранных поверхностей и поверхностей вращения
| Существует три способа построения развертки многогранных поверхностей: | ||
| 1-й способ | 2-й способ | 3-й способ |
| Способ триангуляции (треугольника) | Способ нормального сечения | Способ раскатки |
а) Развертка поверхности многогранника.
Разверткой многогранной поверхности называется плоская фигура, получаемая последовательным совмещением всех граней поверхности с плоскостью.
Так как все грани многогранной поверхности изображаются на развертке в натуральную величину, построение ее сводится к определению величины отдельных граней поверхности – плоских многоугольников.
Метод триангуляции
Пример 1. Развертка пирамиды (рисунок 13.1).
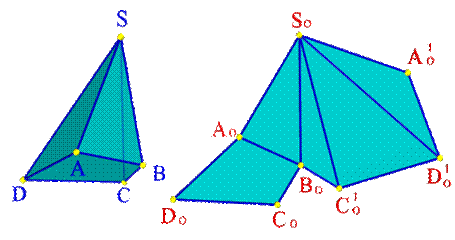
При построении развертки пирамиды применяется способ треугольника. Развертка боковой поверхности пирамиды представляет собой плоскую фигуру, состоящую из треугольников – граней пирамиды и многоугольника — основания. Поэтому построение развертки пирамиды сводится к определению натуральной величины основания и граней пирамиды. Грани пирамиды можно построить по трем сторонам треугольников, их образующих.
Рисунок 13.1. Пирамида и её развертка
Для этого необходимо знать натуральную величину ребер и сторон основания. Алгоритм построения можно сформулировать следующим образом (рисунок 13.2):
| 1 Определяют натуральную величину основания пирамиды (например, методом замены плоскостей проекций) |
| 2 Определяют истинную величину всех ребер пирамиды любым из известных способов (в данном примере натуральная величина всех ребер пирамиды определена методом вращения вокруг оси перпендикулярной горизонтальной плоскости проекций и проходящей через вершину пирамиды S) |
| 3 Строят основание пирамиды и по найденным трем сторонам строят какую-либо из боковых граней, пристраивая к ней следующие (рисунок 13.3). |
Рисунок 13.2. Определение истинной величины
основания и ребер пирамиды
Точки, расположенные внутри контура развертки, находят во взаимно однозначном соответствии с точками поверхности многогранника. Но каждой точке тех ребер, по которым многогранник разрезан, на развертке соответствуют две точки, принадлежащие контуру развертки. Примером первой точки на рисунках служит точка К0 и КÎSАD, а иллюстрацией второго случая являются точки М0 и М0 * . Для определения точки К0 на развертке пришлось по ее ортогональным проекциям найти длины отрезков АМ (метод замены плоскостей проекций) и SК (метод вращения). Эти отрезки были использованы затем при построении на развертке сначала прямой S0М0 и, наконец, точки К0.

Рисунок 13.3. Построение развертки пирамиды
Способ нормального сечения
В общем случае развертка призмы выполняется следующим образом. Преобразуют эпюр так, чтобы ребра призмы стали параллельны новой плоскости проекций. Тогда на эту плоскость ребра проецируются в натуральную величину.
Пример 2. Развертка призмы (рисунок 13.4).
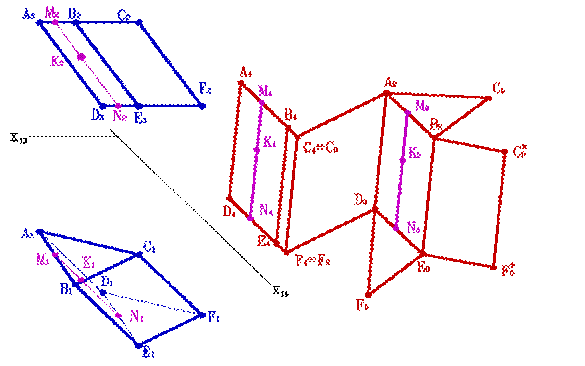
Пересекая призму вспомогательной плоскостью α, перпендикулярной ее боковым ребрам (способ нормального сечения), строят проекции фигуры нормального сечения – треугольника 1, 2, 3, а затем определяют истинную величину этого сечения. На примере она найдена методом вращения.
В дальнейшем строям отрезок 10-10 * , равный периметру нормального сечения. Через точки 10, 20, 30 и 10 * проводят прямые, перпендикулярные 10-10 * , на которых откладывают соответствующие отрезки боковых ребер призмы, беря их с новой фронтальной проекции. Так, на перпендикуляре, проходящем через точку 10, отложены отрезки 10D0=14D4 и 10А0=14А4.. Соединив концы отложенных отрезков, получают развертку боковой поверхности призмы. Затем достраивают основание.
Способ раскатки
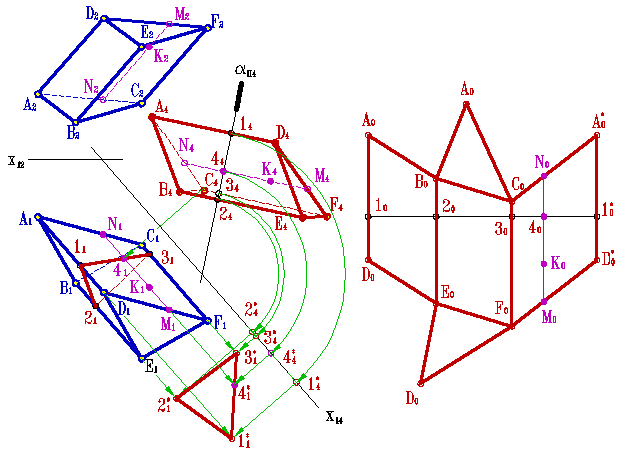
Пример 3. Развертка призмы, частный случай, когда основание призмы на одну из плоскостей проекций проецируется в натуральную величину (рисунок 13.5).
Развертка боковой поверхности такой призмы осуществляется способом раскатки. Этот способ заключается в следующем. Сначала, как и в предыдущем примере, преобразуют эпюр так, чтобы боковые ребра призмы стали параллельны одной из плоскостей проекций.
Рисунок 13.4. Развертка призмы способом нормального сечения

Затем новую проекцию призмы вращают вокруг ребра С4F4 до тех пор пока грань ACDF не станет параллельной плоскости П4.
При этом положение ребра С4F4 остается неизменным, а точки принадлежащие ребру AD перемещаются по окружностям, радиус которых определяется натуральной величиной отрезков AC и DF (так как основания призмы параллельны П1 то на эту плоскость проекций они проецируются без искажения, т.е. R=A1C1=D1F1), расположенных в плоскостях, перпендикулярных ребру С4F4.
Таким образом, траектории движения точек A и D на плоскость П4 проецируются в прямые, перпендикулярные ребру С4F4.
Когда грань ACDFстанет параллельна плоскости П4, она проецируется на неё без искажения т.е. вершины A и D окажутся удаленными от неподвижных вершин C и F на расстояние, равное натуральной величине отрезков AC и DF. Таким образом, засекая перпендикуляры, по которым перемещаются точки A4 и D4 дугой радиуса R=A1C1=D1F1, можно получить искомое положение точек развертки A0 и D0.
Следующую грань АBDE вращают вокруг ребра AD. На перпендикулярах, по которым перемещаются точки B4и E4 делают засечки из точек A0 и D0 дугой радиуса R=A1B1=D1E1. Аналогично строится развертка последней боковой грани призмы.
Процесс последовательного нахождения граней призмы вращением вокруг ребер можно представить как раскатку призмы на плоскость параллельную П4 и проходящую через ребро С4F4.
Построение на развертке точки К, принадлежащей боковой грани АBDE, ясно из рисунка. Предварительно через эту точку по грани провели прямую NМ, параллельную боковым ребрам, которая затем построена на развертке.
б) Развертка цилиндрической поверхности.
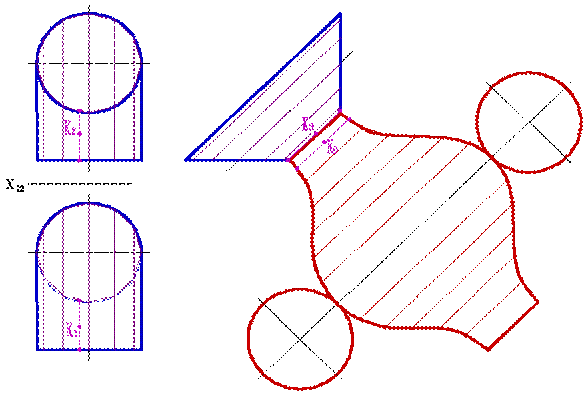
Развертка цилиндрической поверхности выполняется аналогично развертке призмы. Предварительно в заданный цилиндр вписывают n-угольную призму (рисунок 13.6). Чем больше углов в призме, тем точнее развертка (при n →призма преобразуется в цилиндр).
в) Развертка конической поверхности
Развертка конической поверхности выполняется аналогично развертке пирамиды, предварительно вписав в конус n-угольную пирамиду (рисунок 13.6).
Если задана поверхность прямого конуса, то развертка его боковой поверхности представляет круговой сектор, радиус которого равен длине образующей конической поверхности l, а центральный угол φ=360 о r / l, где r – радиус окружности основания конуса.
Рисунок 13.6. Развертка цилиндрической поверхности

| Запомните! Задание | Существует три способа построения развертки: способ нормального сечения, раскатки и треугольника.Дайтехарактеристику каждому из способов. Внимательно рассмотрите примеры, приведенные в лекции. Выполните построения по рисункам 13.1…13.7. |
Контрольные вопросы
1 Что называют разверткой поверхности?
2 Какие поверхности называют развертывающимися и какие – неразвертывающимися?
3 Укажите основные свойства разверток
4 Укажите последовательность графических построений разверток поверхностей конуса и цилиндра.
5 Какие способы построения разверток многогранников вы знаете?
Источник