Для функции заданной табличным способом укажите имеет она обратную или нет

Обратная функция

формировать коммуникативную компетентность

Просмотр содержимого документа
«Обратная функция»

• Образовательна я:
• закрепить знаний по теме в соответствии с программным материалом; продолжить изучать свойства обратимости функции и нахождение функции обратной данной.
• Развивающая:
• овладеть понятием обратной функции и усвоить методы нахождения обратной функции;
• развивать навыки самоконтроля, предметную речь.
• Воспитательная:
• формировать коммуникативную компетентность.

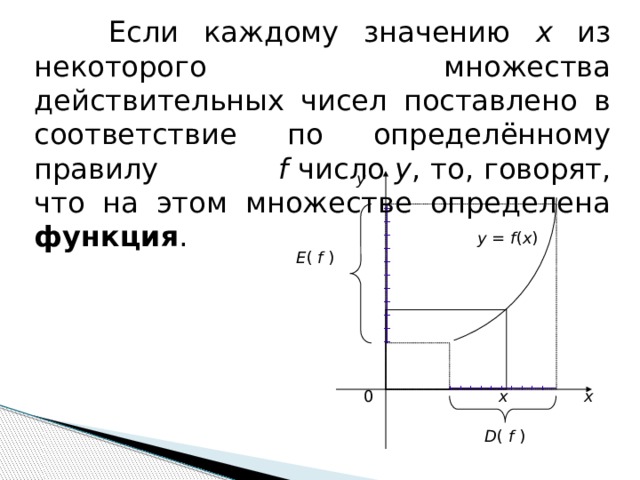
Если каждому значению х из некоторого множества действительных чисел поставлено в соответствие по определённому правилу f число у , то, говорят, что на этом множестве определена функция .

Если функция у = f ( х ) принимает каждое своё значение у только при одном значении х , то эту функцию называют обратимой.

• Пусть у = f ( x ) – обратимая функция. Тогда каждому у из множества значений функции соответствует одно определённое число х из области её определения, такое, что f ( x ) = y . Это соответствие определяет функцию х от у , которую обозначим х = g ( y ). Поменяем местами х и у : у = g ( x ).
• Функцию у = g ( x ) называют обратной к функции у = f ( x ).

Чтобы найти функцию обратную данной нужно:

Свойства обратных функций

• Область определения обратной функции f-1совпадает с множеством значений исходной f, а множество значений обратной функции f-1совпадает с областью определения исходной функции f:

Свойства обратных функций

• Монотонная функция является обратимой:

если функция f возрастает, то обратная к ней функция f -1 также возрастает;

если функция f убывает, то обратная к ней функция f -1 также убывает.

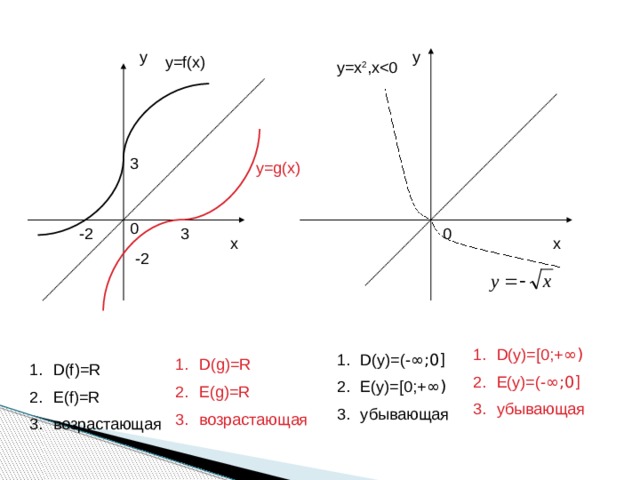
• D(y)=[0;+ ∞)
• E(y)=(- ∞;0]
• убывающая

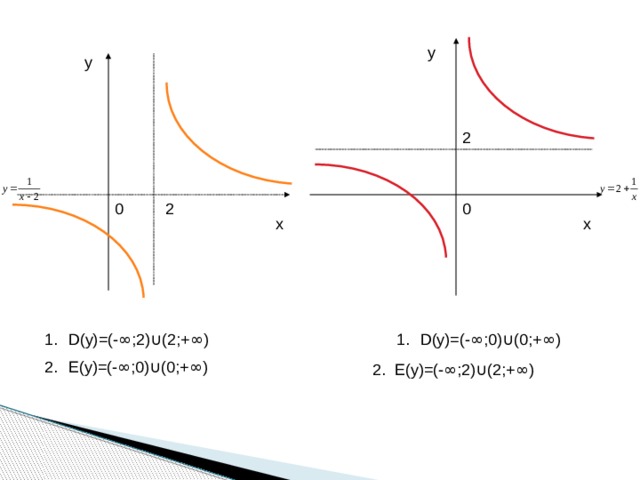
• D(y)=(- ∞;0]
• E(y)=[0;+ ∞)
• убывающая

• D(g)=R
• E(g)=R
• возрастающая

• D(f)=R
• E(f)=R
• возрастающая

Свойства обратных функций

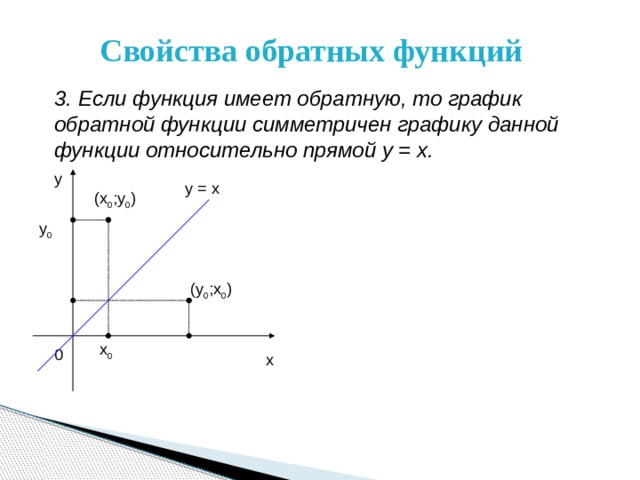
3. Если функция имеет обратную, то график обратной функции симметричен графику данной функции относительно прямой у = х.

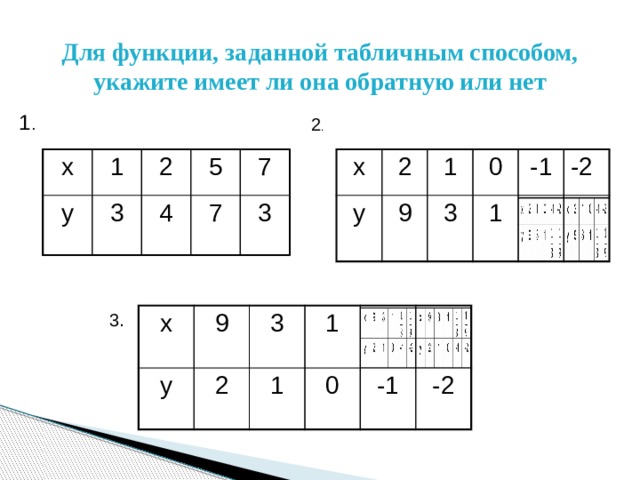
Для функции, заданной табличным способом, укажите имеет ли она обратную или нет

Источник

Функция x f у у g x g(x) = f -1 (x). А роза упала на лапу Азора 2. — презентация

Презентация была опубликована 8 лет назад пользователемЛеонид Карпенко

Похожие презентации

Презентация на тему: » Функция x f у у g x g(x) = f -1 (x). А роза упала на лапу Азора 2.» — Транскрипт:

1 Функция x f у у g x g(x) = f -1 (x)

2 А роза упала на лапу Азора 2

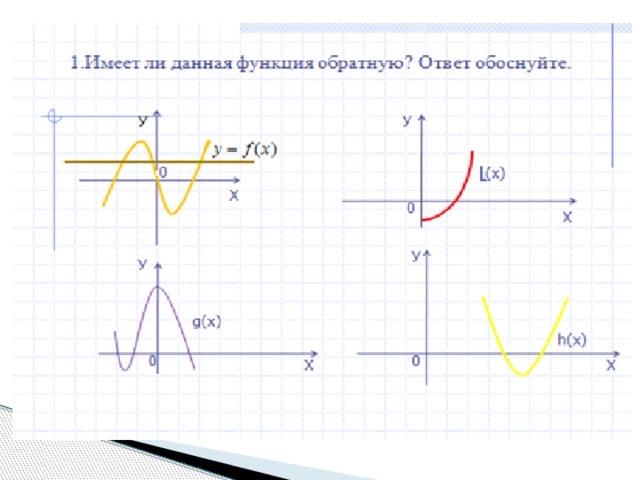
3 Х 1 0 У 0 1.Имеет ли данная функция обратную? Ответ обоснуйте. 2.Если прямая функция возрастает, то и обратная Графики взаимно обратных функций симметричны относительно … 3.Если прямая функция убывает, то и обратная. Х 1

4 Обратная функция. Упражнения. 1. Определите по графику функции, какая имеет обратную, а какая нет. У У У У 1) 2) 3) 4) f(x) g(x) h(x) y(x) 0 X 0 X 0 X 0 X 2. Для функции, заданной табличным способом, укажите имеет она обратную или нет; в случае положительного ответа, постройте график обратной функции: 1) 2) х1257 у3473 х9311/31/9 у210-2 х210-2 у9311/31/9

5 3.Для функции у = х 3, х 0 найдите обратную и постройте графики обеих функций. 4. Для функции у = найдите обратную. 5.(Дополнительное задание) Для функции найдите обратную и постройте графики обеих функций.

6 Ответы к зданиям 3 и 4. 1) у =, если х 0; 2) или У У У 0 Х 2 у = х X X y = D(y) = D(y) = E(y) = E(y) =

7 6. Дано: f(x) = и f -1(x) = g(x) =. Найти область определения и множество значений данных функций.

8 1. Для функции, заданной табличным способом, укажите имеет она обратную или нет; в случае положительного ответа постройте график обратной функции: 1) 2) 2. Для заданной функции найдите обратную функции: 1) у = 2 + 4х; 2) у = 5х + 2; 3) у = ; 4) у =. 3. Для функции у = f(x), график которой изображен на рисунке, постройте график обратной функции. Y Y X X На каждом из указанных промежутков найдите, если это возможно, функцию обратную 1) (-; 0]; R; 2) [0; +); R. х у1/21248 х84210,50,25 у В каждом задании выполнить нечетные номера – вариант1, четные номера – вариант2

9 1. Y Y 1) 1 2) X 0 1 X 2. 1) у = 2 + 4х; или ; 2) у = 5х + 2; или ; 3) у = ;. 4) у = ;. 3. Y Y Y 6 1 y = f(x) 0 1 Х y = f (x) X X

10 Задание на с/п 1. Задайте функцию табличным способом, так чтобы она имела обратную и нет (в).Постройте график функции и прочтите его, у =, если данная функция имеет обратную, то постройте ее график. 3* (а). y = 3x + |x|. Математику нельзя изучать, наблюдая, как это делает сосед! А. Нивен

11 5.(Д/з) Для функции найдите обратную и постройте графики обеих функций. 210 У X 2 1

Источник

Презентация по математике для 10 класса «Числовые функции»

Описание презентации по отдельным слайдам:

Числовые функции Установить соответствие и задать функцию означает одно и тоже. Маркушевич А. И Урок разработан учителем математики МБОУ «СОШ №34», г. Бийска Алтайского края Масловой Светланой Константиновной, при участии учащихся 10 класса (Пановой В, Галкиной А, Ралдугина И, Хисамутдинова А)

«Определение числовой функции и способы её задания» Учащийся 10 класса Хисамутдинов А

Определение 1 Если даны числовое множество Х и правило f, позволяющее поставить в соответствие каждому элементу х из множества Х определённое число у, то говорят, что задана функция у = f (x) с областью определения Х. Область определения функции обозначают D (f). Множество всех значений функций у = f (x), х є Х называют областью значений функции и обозначают E (f). Учащийся 10 класса Хисамутдинов А

Способы задания функции. Аналитический. Графический. Табличный. Учащийся 10 класса Хисамутдинов А

Определение 2 Если дана функция у = f (x), x принадлежит Х и на координатной плоскости х О у отмечены все точки вида (х ; у), где х принадлежит Х, а у = f (x), то множество этих точек называют графиком функции у = f (x), x принадлежит Х. Учащийся 10 класса Хисамутдинов А

Пример Построить график функции Решение. Учащийся 10 класса Хисамутдинов А

№1. Выясните, на каком рисунке указаны графики функций y=f(x). Укажите область определения и область значения этих функций (за единицу масштаба принять размер одной клетки). Ответ: a) D(f)=(-3;3], E(f)=(-1;3], в) D(f)=[-1; +∞), E(f)=[-2; +∞). Урок учителя математики Масловой С. К.

№2. Найдите область определения функций Ответ: [12; +∞) Ответ: [-12;-1)U(-1;1) U(1; +∞) Урок учителя математики Масловой С. К.

Учащаяся 10 класса Панова В

1. D (f) = [-4; +∞) 2. E (f) = [ 0; +∞) 3. у= 0, при х = -4 4. у> 0, при х є ( -4; +∞) 5. Возрастает при х є [-4; 0] u [3;+∞) Убывает при х є [ 0; 3] 6. унаиб — не существует, унаим = 0 7. Функция ни четная и ни нечетная 8. уmax=4 , уmin= 1 9. Функция не периодическая 10. Функция ограничена снизу 11. Функция непрерывна 12. Функция выпукла вверх при х є [-4;0], функция выпукла вниз при х є [ 0; 3] 13. Асимптот нет. Учащаяся 10 класса Панова В

Ответ: б). №3. Укажите график нечетной функции Урок учителя математики Масловой С. К.

Периодические функции. Функцию, имеющую отличный от нуля период Т, называют переодической. Если функция у = f(х), хХ имеет период Т, то любое число, кратное Т(т.е. число вида kТ, kєZ), также является её периодом. выполняются равенства: f(х — Т) = f(х) = f(х + Т) Учащаяся 10 класса Галкина А

Пример. Доказать, что функция у = <х>– периодическая. Решение. Числа х и х ± k, где k – любое целое число, имеет одинаковую дробную часть, т. е. <х - k>= <х>= <х + k>. Значит, любое целое число является периодом функции; есть и основной период: Т = 1. Учащаяся 10 класса Галкина А

№4. Постройте график периодической функции f(x)=ІxІ с периодом 2 на отрезке [-1;1]. Укажите её свойства. Урок учителя математики Масловой С. К.

Учащийся 10 класса Ралдугин И

Учащийся 10 класса Ралдугин И

Если функция y=f(x) монотонна на множестве X, то она обратима. Учащийся 10 класса Ралдугин И

Показать ,что для функции y=5x-3 существует обратная функция ,и найти её аналитическое выражение. Решение. Линейная функция Y=5X-3 определена на R,возрастает на R и область её значений есть R. Значит , обратная функция существует на R. Чтобы найти её аналитическое выражение ,решим уравнение Y=5X-3 относительно x; получим:X=(y+3)/5.Это и есть искомая обратная функция. Она определена и возрастает на R. Учащийся 10 класса Ралдугин И

№5. Для функции, заданной табличным способом, укажите её область значений и определите имеет ли она обратную функцию? а) б) Ответ: а) нет, б) да. Урок учителя математики Масловой С. К. х 1 2 5 7 У 3 4 7 3 х 1 2 3 7 у 5 8 9 1

№6. у = f(x) и y = g(x) – взаимно-обратные функции, причем f(5) = 8 и g(7) = 1. Решите уравнения f(3x) = 7 и g(5-x) = 5. Ответ: 1/3, -3. Урок учителя математики Масловой С. К.

Ответы к тесту. Вариант 1. Шкала оценок Вариант 2. Урок учителя математики Масловой С. К. № задания 1 2 3 4 5 6 7 Прав. ответ 2 3 2 3 1 3 2 № задания 1 2 3 4 5 6 7 Прав. ответ 2 4 3 1 4 3 1 Кол-во ошибок Оценка 0 5 1 4 2-3 3

Домашнее задание. Учебник 10 класса Алгебра и начала анализа (в 2-х частях) А.Г. Мордкович, П.В. Семенов. Глава 2, № 7.29, 8.21, 8.34, 9.28, 10.27 (в), 8.32 (б). Урок учителя математики Масловой С. К.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 798 человек из 78 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 281 человек из 70 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 605 человек из 75 регионов

Ищем педагогов в команду «Инфоурок»

Презентация к уроку математики в 10 классе по теме «Числовые функции», учителя МБОУ «СОШ №34» города Бийска Алтайского края Масловой С.К., составлена совместно с учащимися. Урок носит обобщающий характер и является подготовительным к контрольной работе по данной теме. В уроке использованы элементы самоконтроля и взаимоконтроля, задания из Единого государственного экзамена, в конце урока проводиться небольшое тестирование. Учащиеся повторяют полностью такие подтемы как определение и способы задания числовой функции, обратная и периодическая функции, исследование числовой функции.

Номер материала: 37623032501

Международная дистанционная олимпиада Осень 2021

Не нашли то что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Безлимитный доступ к занятиям с онлайн-репетиторами

Выгоднее, чем оплачивать каждое занятие отдельно

Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст

Время чтения: 1 минута

В Пензенской области запустят проект по снижению административной нагрузки на учителей

Время чтения: 1 минута

На новом «Уроке цифры» школьникам расскажут о разработке игр

Время чтения: 1 минута

В Минпросвещения предложили организовать телемосты для школьников России и Узбекистана

Время чтения: 1 минута

Минпросвещения разрабатывает образовательный минимум для подготовки педагогов

Время чтения: 2 минуты

В Северной Осетии организовали бесплатные онлайн-курсы по подготовке к ЕГЭ

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник