Длина отрезка двумя способами

Отрезок. Длина отрезка

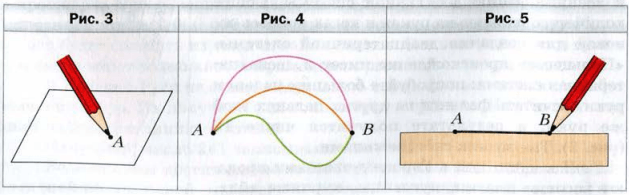
Если вы хорошо заточенным карандашом прикоснетесь к тетрадному листу, то останется след, который дает представление о точке. (рис. 3 ).

Отметим на листе бумаги две точки A и B. Эти точки можно соединить различными линиями (рис. 4 ). А как соединить точки A и B самой короткой линией? Это можно сделать с помощь линейки (рис. 5 ). Полученную линию называют отрезком.

Точка и отрезок − примеры геометрических фигур.

Точки A и B называют концами отрезка.

Существует единственный отрезок, концами которого являются точки A и B. Поэтому отрезок обозначают, записывая точки, которые являются его концами. Например, отрезок на рисунке 5 обозначают одним из двух способов : AB или BA. Читают: «отрезок AB» или «отрезок BA».

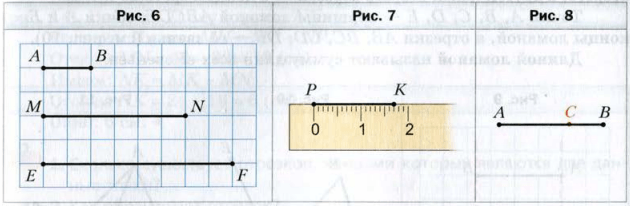
На рисунке 6 изображены три отрезка. Длина отрезка AB равна 1 см. Он помещается в отрезке MN ровно три раза, а в отрезке EF − ровно 4 раза. Будем говорить, что длина отрезка MN равна 3 см, а длина отрезка EF − 4 см.

Также принято говорить: «отрезок MN равен 3 см», «отрезок EF равен 4 см». Пишут : MN = 3 см , EF = 4 см.

Длины отрезков MN и EF мы измерили единичным отрезком, длина которого равна 1 см. Для измерения отрезков можно выбрать и другие единицы длины, например: 1 мм, 1 дм, 1 км. На рисунке 7 длина отрезка равна 17 мм. Он измерен единичным отрезком, длина которого равна 1 мм, с помощью линейки с делениями. Также с помощью линейки можно построить (начертить) отрезок заданной длины (см. рис. 7 ).

Вообще, измерить отрезок означает подсчитать, сколько единичных отрезков в нем помещается.

Длина отрезка обладает следующим свойством.

Если на отрезке AB отметить точку C, то длина отрезка AB равна сумме длин отрезков AC и CB (рис. 8 ).

Пишут : AB = AC + CB.

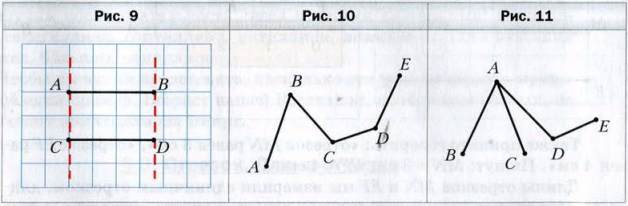
На рисунке 9 изображены два отрезка AB и CD. Эти отрезки при наложении совпадут.

Два отрезка называют равными, если они совпадут при наложении.

Следовательно отрезки AB и CD равны. Пишут : AB = CD.

Равные отрезки имеют равные длины.

Из двух неравных отрезков бОльшим будем считать тот, у уоторого длина больше. Например, на рисунке 6 отрезок EF больше отрезка MN.

Длину отрезка AB называют расстоянием между точками A и B.

Если несколько отрезков расположить так, как показано на рисунке 10, то получится геометрическая фигура, которую называют ломаная . Заметим, что все отрезки на рисунке 11 ломаную не образуют. Считают, что отрезки, образуют ломаную, если конец первого отрезка совпадает с концом второго, а другой конец второго отрезка − с концом третьего и т. д.

Точки A, B, C, D, E − вершины ломаной ABCDE, точки A и E − концы ломаной , а отрезки AB, BC, CD, DE − ее звенья (см. рис. 10 ).

Длиной ломаной называют сумму длин всех ее звеньев.

На рисунке 12 изображены две ломаные, концы которых совпадают. Такие ломаные называют замкнутыми.

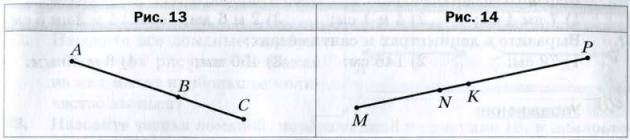
Пример 1 . Отрезок BC на 3 см меньше отрезка AB, длина которого равна 8 см (рис. 13 ). Найдите длину отрезка AC.

Решение. Имеем : BC = 8 − 3 = 5 (см).

Воспользовавшись свойством длины отрезка, можно записать AC = AB + BC. Отсюда AC = 8 + 5 = 13 (см).

Пример 2 . Известно, что MK = 24 см , NP = 32 см , MP = 50 см (рис. 14 ). Найдите длину отрезка NK.

Источник

Математика. 6 класс

Конспект урока

Перечень рассматриваемых вопросов:

• длина отрезка;
• единицы измерения длины;
• способы измерения длины отрезка;
• решение задач на вычисление длины отрезка.

Отрезок – это часть прямой, ограниченная двумя точками.

Длина отрезка – это расстояние между его концами.

Измерение длины отрезка – это сравнение длины отрезка с выбранной единицей измерения.

Длиной отрезка называется положительная величина, определённая для каждого отрезка.

Любой отрезок имеет определённую длину, большую нуля.

1. Никольский С. М. Математика. 6 класс. Учебник для общеобразовательных учреждений // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017, стр. 258.

1. Чулков П. В. Математика: тематические тесты.5-6 кл. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина – М.: Просвещение, 2009, стр. 142.
2. Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. // И. Ф. Шарыгин, А. В. Шевкин – М.: Просвещение, 2014, стр. 95.

Теоретический материал для самостоятельного изучения

Что такое отрезок?

Отрезок – это часть прямой, ограниченная двумя точками.

Как отрезки обозначаются на чертежах?

Отрезок можно обозначить двумя заглавными буквами – отрезок АВ. Или можно обозначить отрезок одной строчной буквой – отрезок с.

Любой отрезок имеет определённую длину, большую нуля.

Длина может быть выражена натуральным или дробным числом.

Измерить отрезок – значит найти его длину.

Длина отрезка – это расстояние между его концами.

Свойства длин отрезков:

– равные отрезки имеют равные длины;

– если отрезок состоит из двух отрезков, то его длина равна сумме длин его частей.

Эти свойства длины отрезка используются при её измерении. Чтобы измерить длину отрезка, нужно выбрать единицу длины.

Такой единицей может быть длина произвольного отрезка. В мультфильме «38 попугаев» герои измеряли длину удава в попугаях.

Для определения длины отрезка надо узнать, сколько раз в данном отрезке помещается выбранная единица измерения.

Можно сравнивать длины отрезков, не имея под рукой линейки. Например, прикладывать к отрезкам один и тот же карандаш, ластик или использовать циркуль. Для этого нужно установить иглу в начало отрезка, провести дугу, пересекающую отрезок, затем, не меняя расстояния между иглой и карандашом циркуля, переставить иглу в точку пересечения и повторить действия.

В десятичной системе мер единицами измерения длины являются 1 мм, 1 см, 1 дм, 1 м и т. д.

Рассмотрим несколько примеров измерения длины отрезка. Измерения небольших отрезков удобно производить с помощью линейки.

Прикладываем линейку так, чтобы один конец отрезка совместился с нулём. Единичный отрезок 1 см отложился 7 раз, значит, длина отрезка АВ = 7 см.

Если единичный отрезок 1 см отложился n раз, и осталась часть меньшая 1 см, то откладываем отрезки равные 1/10 см. Длина отрезка СD = 8,7 см.

При необходимости можно продолжить откладывать по 1/100 части единичного отрезка и т. д.

Алгоритм измерения длины отрезков:

– выбрать какой-либо отрезок и принять его за единицу длины;

– от одного из концов отрезка отложить последовательно отрезки, равные единичному;

– если единичные отрезки отложились n раз и конец последнего совпал с концом измеряемого отрезка, то значение его длины равно n единиц длины;

– если отрезок или его часть меньше единичного отрезка, то нужно отложить отрезки, равные 1/10 части единичного отрезка;

– если десятые части единичного отрезка отложились ровно n раз, то длина измеряемого отрезка есть конечная десятичная дробь, в которой целая часть равна количеству целых единичных отрезков, а после запятой в разряде десятых стоит количество десятых частей единичного отрезка;

– при необходимости можно откладывать 1/100 часть единичного отрезка и т. д.

Таким образом, для каждого положительного действительного числа существует отрезок, длина которого выражается этим числом.

И для каждого положительного действительного числа существует отрезок, длина которого выражается этим числом.

На практике используют приближённое значение длин отрезков, например, с точностью 1/10 или 1/100 части единичного отрезка, но точность приближения зависит от поставленной задачи.

Рассмотрим фигуры, составленные из отрезков.

Возьмем на плоскости несколько точек и соединим их отрезками. Если никакие два из этих отрезков, имеющих общие точки, не лежат на одной прямой, то линию называют ломаной.

Отрезки, из которых состоит ломаная, называются звеньями, а концы этих отрезков – вершинами ломаной.

Длина ломаной – это сумма длин всех её звеньев.

Если концы ломаной совпадают, то такая ломаная называется замкнутой.

Замкнутая ломаная линия, у которой звенья не пересекаются между собой, называется многоугольником.

Периметр многоугольника равен сумме длин всех его сторон.

Разбор заданий тренировочного модуля

Тип 1. Ввод с клавиатуры пропущенных элементов в тексте.

Впишите верный ответ.

Точка P лежит на отрезке AB. Известно, что отрезок AP больше отрезка PB на 3,6 см, а отрезок AB = 10,4 см. Найдите длину отрезка PB.

Пусть PB = x, тогда AP = x + 3,6 см.

По условию AB = 10,4 см.

Если отрезок состоит из двух отрезков, то его длина равна сумме длин его частей.

Составим и решим уравнение:

Значит, длина отрезка PB = 3,4 см.

Тип 2. Множественный выбор

Выберите верные ответы.

Известно, что отрезок AС = 3,6 см, а отрезок BС = 7,5 см. Найдите длину отрезка АB, если все три точки лежат на одной прямой.

Варианты ответов: 3,9; 11,1; 4,8; 13,2; 16,5; 2,9.

Первый вариант решения

В этом случае АВ = АС + ВС = 3,6 + 7,5 = 11,1 (см).

АВ = ВС – АС = 7,5 – 3,6 = 3,9 (см).

Значит, длина отрезка АВ может быть равна 11,1 см или 3,9 см. Выбираем эти варианты.

Источник

Отрезок. Формула длины отрезка.

Отрезком обозначают ограниченный двумя точками участок прямой. Точки – концы отрезка.

Общеизвестный факт, что каждая точка А плоскости имеет свои координаты (х, у).

В данном примере вектор AB задан координатами (х₂— х₁, y₂— y₁). Квадрат длины вектора будет равен сумме квадратов его координат. Следовательно, расстояние d между точками А и В, или, что то же самое, длина вектора АВ, вычисляется согласно формуле:

Эта формула длины отрезка предоставляет возможность рассчитывать расстояние между двумя произвольными точками плоскости, при условии, что известны координаты этих точек

Вышеуказанную формулу длины отрезка можно доказать и другим способом. В системе координат заданы координаты крайних точек отрезка координатами его концов(х₁y₁) и (х₂,у₂).

Прочертим прямые лини через эти точки перпендикулярно к осям координат, в результате имеем прямоугольный треугольник. Первоначальный отрезок является гипотенузой образовавшегося треугольника. Катеты треугольника сформированы отрезками, их длиной будет проекция гипотенузы на оси координат.

Установим длину этих проекций.

На ось у длина проекции равна y₂ — y₁, а на ось х длина проекции равна х₂ — х₁. На основании теоремы Пифагора видим, что |AB|² = (y₂ – y₁)² + (x₂ – x₁)².

В рассмотренном случае |AB| выступает длиной отрезка.

Вычислим длину отрезка АВ, для этого извлечем квадратный корень. Результатом является все та же формула длины отрезков по известным координатам конца и начала.

Источник

Как сравнить два отрезка: способы и примеры

Отрезок — часть прямой, ограниченная двумя точками, кратчайшее расстояние между этими точками. Существует несколько способов сравнения геометрических фигур, выбор такого способа зачастую зависит не только от условия задачи, но и от возможностей. Как же сравнивать отрезки, расскажем в этой статье.

Способы сравнения двух отрезков

В геометрии две фигуры, имеющие одинаковый размер и форму, называются равными. Сравнение фигур дает возможность сказать, одинаковы ли они. Одним из способов является наложение. Если фигуры удается совместить наложением, они считаются равными.

Сравнить фигуры — значит, определить, которая из них длиннее или короче. Ответ должен быть определенным, нельзя сказать, что один отрезок длиннее или равен второму. В математике такой ответ неправилен, его можно приравнять к отсутствию ответа.

Записывают результат сравнения с помощью знаков больше, меньше и знака равенство (>; АБ.

Сравнивать фигуры можно разными способами, выбор которых зависит от возможностей или условий:

• визуальный способ;
• измерительный;
• сравнение наложением;
• сравнение в координатной сетке.

Лучше всего, если они различаются по длине визуально, и, просто посмотрев на них, вы можете сказать, который длиннее. Но так бывает не всегда.

Измерение длины

Самый простой способ — измерение. Для этого можно использовать линейку, просто измерив длину отрезка, мы поймем, который из них длиннее. Если нет линейки, но они начерчены на листе в клетку, для измерения их длин можно посчитать клетки. В одном сантиметре две клетки. Это метод сравнения измерением длин, но есть еще метод сравнения наложением.

Обратите внимание: что такое луч в геометрии.

Наложение друг на друга

Как происходит совмещение АБ и ВГ:

• Нужно конец, А одного из них совместить с концом В другого, если совпадают и другие концы этих отрезков — Б и Г, значит, они равны, что записывается с помощью знака равно.
• Если нет, значит, один из них длиннее другого, и записывается это также с помощью математических знаков больше или меньше (> или

Сравнение в координатной сетке

Допустим, что у нас есть два отрезка, координаты которых мы знаем — а (Х1, Y1; Х2, Y2) и b (Х3, Y3; X4, Y4).

Первое, что нужно сделать — придать координатам числовые значения:

• Длина, а — Da = √((X1 — X2) ² + (Y1 — Y2) ²);
• Длина b — Db = √((X3 — X4) ² + (Y3 — Y4) ²).

Пусть X1 = -7, Y1 = 4, X2 = 3, Y2 = -4, X3 = -3, Y3 = -5, X4 = 0, Y4 = -3. Получаем:

Da = √ ((-7 — 3) ² + (4 — (-4)) ²) = √ (-10 ² + 8 ²) = √ 100 + 64 = √ 164

Db = √ ((-3 — 0) ² + (-5 — (-3)) ²) = √ (-3 ² + (-8) ²) = √ (9+ 64) = √ 73

√ 164 > √ 73, значит, Da > Db.

Также можно сравнить отрезки, находящиеся в трехмерной системе координат, надо учитывать не две, а три координаты каждого из них.

Примеры

Рассмотрим сравнение методом наложения. У нас имеется два отрезка — АБ и ВГ.

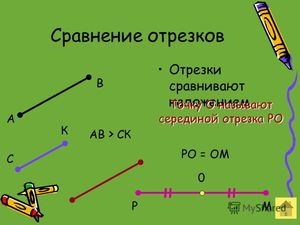
Чтобы узнать, равны они или нет, просто приложим их друг к другу так, чтобы их «начала» были в одной точке, то есть совместим точки, А и В.

Если мы видим, что АБ получается частью ВГ, значит, он меньше, то есть АБ 2, значит, CD>AB, то есть отрезок CD длиннее AB.

Источник