Дискретный способ представления информации системы счисления

Дискретный способ представления информации системы счисления

Код ОГЭ: 1.1.3 Дискретная форма представления информации. Единицы измерения количества информации

Информация может быть представлена в аналоговой или дискретной форме. Величина в аналоговой форме может принимать бесконечное множество значений. Примерами аналогового представления информации могут служить звук скрипки, картина художника, показатели температуры воздуха, уровня воды в реке.

Величина в дискретной форме может принимать только конечное множество значений. Примеры дискретного представления информации: цифровые показания часов или спидометра, текст в книге, изображение на экране монитора.

Величину в аналоговой форме представления информации можно преобразовать в величину в дискретной форме. Этот процесс называется дискретизацией.

Представление информации в компьютере дискретно . В процессах хранения, обработки и передачи информации в компьютере используется двоичная знаковая система. Ее алфавит состоит всего из двух знаков <0, 1>. Для удобства использования такого алфавита договорились называть любой из его знаков бит (от англ. bit — binary digit — двоичный знак). Поскольку один бит может принимать только одно из двух значений, то им выражают одно из двух взаимоисключающих понятий: да/нет, истина/ложь, включено/выключено.

Способ представления информации с помощью кода из двух знаков оказался наиболее значимым для развития техники. Двоичные числа удобно хранить, обрабатывать и передавать с помощью электронных устройств. Основным носителем информации в них являются элементы, которые могут находиться в одном из двух состояний: включено/выключено, высокий/низкий уровень напряжения или тока, наличие/отсутствие намагниченности материалов. Условно одно состояние обозначают через 1, а другое через 0. Каждый такой элемент способен хранить один двоичный разряд, или бит информации.

Любое информационное сообщение представляется последовательностью нулей и единиц (цифрового кода). Этот метод представления информации называется двоичным кодированием. Таким образом, двоичный код является универсальным средством кодирования информации. Благодаря двоичному кодированию все действия по обработке сообщений компьютером сводятся к совокупности простых действий над 0 и 1.

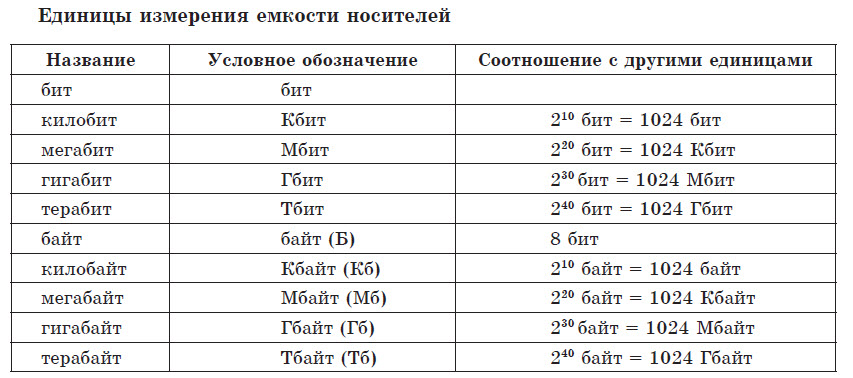
Единицы измерения количества информации

Основной единицей хранения и обработки цифровой информации принят байт.

Соответственно, с помощью одного байта можно получить 256 (= 2 8 ) двоичных значений (от 00000000 до 11111111). В современных персональных компьютерах байт является наименьшей совокупностью битов, которую компьютер обрабатывает одномоментно.

На практике применяют более емкие, чем байт, единицы измерения объема сообщений и емкости носителей — килобайты, мегабайты, гигабайты, терабайты. Множителем при переходе к более емкой единице измерения выступает число 1024 (= 2 10 ).

Системы счисления

Система счисления — совокупность обозначений, приемов и правил для записи чисел цифровыми знаками. В зависимости от способов изображения чисел цифрами системы счисления делятся на непозиционные и позиционные.

Непозиционные системы счисления — такие, в которых количественное значение каждой цифры не зависит от занимаемой ею позиции в изображении числа.

Примером может служить египетская система счисления — в ней иероглифы (цифры), составляющие число, можно записывать сверху вниз, справа налево или вперемежку. Значение числа равно сумме значений цифр в его записи.

Переходной от непозиционных систем к позиционным служит римская система счисления. В ней позиция некоторых цифр уже меняет значение числа: например, в числе IX единицу нужно отнять от десяти, а в числе XI единицу нужно прибавить к десяти. Однако количественное значение самих цифр Х и I от их позиции не зависит.

В римской системе цифры записываются слева направо в порядке убывания, и тогда их значения складываются. Если слева записана меньшая цифра, а справа — большая, то их значения вычитаются. Нежелательно записывать более трех одинаковых цифр подряд.

Например, для представления числа 348 в римской системе счисления надо выписать сначала число сотен, затем десятков и единиц: 300 — ССС, 40 — ХL, 8 — VIII. Затем соединить эти записи: CCCXLVIII. Аналогично для числа 1977: 1 тысяча — М, 900 — СМ, 70 — LXХ, 7 — VII. Результат: MCMLXXVII.

В непозиционных системах очень трудно производить многие действия над числами, особенно умножение и деление, слишком громоздка запись для больших чисел. Поэтому широкое распространение получили позиционные системы счисления.

Позиционные системы счисления — такие, в которых количественное значение каждой цифры зависит от ее позиции в числе.

Количество знаков (цифр), используемых для изображения числа, называется основанием системы счисления (или мощностью алфавита). Систему с основанием 10 называют десятичной, с основанием 2 — двоичной, с основанием 16 — шестнадцатеричной, в общем случае: с основанием k — k-ичной.

Место цифры в числе называется разрядом, а количество цифр в числе — его разрядностью. Разряды целого числа нумеруются справа налево начиная с 0. Дробные разряды нумеруют слева направо начиная с -1.

Примером позиционной системы счисления является используемая нами арабская десятичная система счисления. Иногда ее называют индо-арабской, поскольку она была придумана в Индии, а стала известна в Европе из арабских трактатов. Алфавит этой системы составляют 10 цифр — от 0 до 9. Каждая цифра в числе при перемещении справа налево в следующий разряд увеличивает свое значение в 10 раз. Чтобы определить значение числа, надо сложить произведения каждой его цифры на 10 в степени, равной разряду этого числа.

348 = 3 • 10 2 + 4 • 10 1 + 8 • 10 0

–348,17 = –(3 • 10 2 + 4 • 10 1 + 8 • 10 0 + 1 • 10 –1 + 7 • 10 –2 )

Системы счисления могут иметь различные основания. Чтобы различать, в какой системе счисления записано число, принято указывать ее основание в виде нижнего индекса справа от числа. Сам индекс всегда представляется в десятичной системе. Для самой десятичной системы индекс указывают только тогда, когда используется какая–либо другая система:

316 — число в десятичной системе счисления,
316₈ — число в восьмеричной системе счисления.

Свойства записи чисел в позиционной системе счисления:

1. Для записи чисел в позиционной системе счисления с основанием k требуется k знаков (алфавит системы состоит из k цифр или букв).
2. Основание системы счисления, записанное в ней, всегда имеет вид 10 (читается «один ноль»).
3. С помощью n разрядов в позиционной системе счисления с основанием k могут быть записаны k n чисел (от 0 до k n–1 ).

Если основание системы k больше 10, то цифры старше 10 при записи обозначают прописными буквами латинского алфавита: A, B, …, Z. При этом цифре 10 соответствует знак A, цифре 11 — знак B и т. д.

Информация в компьютере представлена в цифровой двоичной форме. В целях экономичного отображения двоичную информацию можно представлять в шестнадцатеричном виде. В программировании часто используется восьмеричная запись чисел.

В общем виде число в позиционной системе счисления может быть представлено как последовательность символов алфавита (цифр), обозначенных через а₁, а₂, а₃ и т. д. Для числа А с количеством целых разрядов n и количеством дробных разрядов m запись имеет вид:

Такая запись называется свернутой записью числа. Эту форму записи мы используем в повседневной жизни, поэтому ее называют также естественной.

Представление числа в виде многочлена называют развернутой записью числа:

Развернутая запись числа задает правило для вычисления числа по его цифрам в k–ичной системе счисления. Для уменьшения количества вычислений пользуются схемой Горнера, которая получается путем поочередного выноса основания системы k за скобки:

Конспект урока по информатике «Дискретная форма представления информации».

Источник

Универсальность дискретного (цифрового) представления информации. Представление информации в двоичной системе счисления

Просмотр содержимого документа
«Универсальность дискретного (цифрового) представления информации. Представление информации в двоичной системе счисления»

Универсальность цифрового представления информации

Для передачи информации используется физический процесс, который может быть описан математической формулой и называется сигналом.

Именно сигналы различают по способу их представления как аналоговые и дискретные.

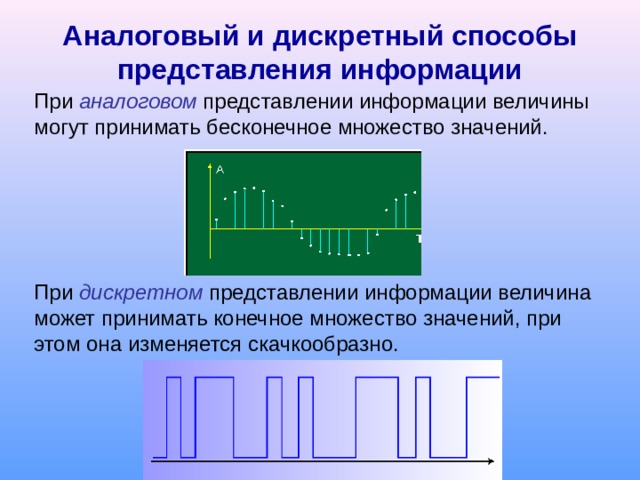
Аналоговый и дискретный способы представления информации

При аналоговом представлении информации величины могут принимать бесконечное множество значений.

При дискретном представлении информации величина может принимать конечное множество значений, при этом она изменяется скачкообразно.

Двоичное представление информации

Количество символов: N =2

Информационный вес символа:

Каждая буква алфавита ( 0 1) несет один бит информации.

Некоторое число в двоичной системе счисления записывается как 1001010. Определите это число и запишите его в ответе в десятичной системе счисления.

Воспользовавшись правилом развёрнутой записи чисел, переведём двоичное число в его десятичное представление:

2. Некоторое число в двоичной системе счисления записывается как 10111. Определите это число и запишите его в ответе в десятичной системе счисления.

3. Некоторое число в двоичной системе счисления записывается как 111010. Определите это число и запишите его в ответе в десятичной системе счисления.

3. Некоторое число в восьмеричной системе счисления записывается как 53 8 . Определите это число в десятичной системе счисления и запишите его в ответе.

4. Некоторое число в восьмеричной системе счисления записывается как 37 8 . Определите это число и запишите его в ответе в десятичной системе счисления.

Универсальность цифрового представления информации

Какого вида информация может быть представлена в виде двоичного кода?

• текст
• графика
• звук
• видео

Для обработки текстовой информации на компьютере необходимо представить её в двоичной знаковой системе.

Unicode — это «уникальный код для любого символа, независимо от платформы, независимо от программы, независимо от языка» .

в таблицу ASCII: 1 байт (8 бит)

Часто используемые символы: 2 байта (16 бит)

Символы, не входящие в таблицу ASCII: 2-4 байта (16-32 бит)

Редко используемые символы: 4 байта (32 бит)

Информационный объем сообщения

Информационный объём сообщения — количество бит (байт, килобайт, мегабайт и т. д.), необходимых для записи этого сообщения.

i – информационный вес символа

N – мощность алфавита (количество символов в алфавите)

K – количество символов в сообщении

I – информационный объём сообщения

Каков информационный объем сообщения

Я помню чудное мгновенье.

при условии что слова разделяются 1 пробелом, а информационный вес символа равен 8 бит (алфавит клавиатуры)?

I = 25 x 1 б = 25 б . Ответ: I = 25 б .

1 . Для передачи сообщения использовалась кодировка Unicode ( N = 65536). Сообщение заняло 10 страниц, на каждой из которых 64 строки по 32 символа. Каков информационный объём сообщения? Ответ дать в килобайтах.

2. Количество информации в сообщении, содержащем 2048 символов, составляет 1/512 часть мегабайта.

Какова мощность алфавита, с помощью которого записано сообщение?

Дискретное представление графической информации

Изображение на экране монитора дискретно. Оно составляется из отдельных точек – пикселей.

Пиксель – минимальный участок изображения, которому независимым образом можно задать цвет.

В процессе дискретизации могут использоваться разные палитры.

Палитра ( N ) – количество цветов, которые могут быть использованы для воспроизведения изображения.

Глубина цвета ( i ) – количество бит, используемое для представления цвета при кодировании одного пикселя.

Определить количество цветов в 24-битовой палитре.

N = 2 24 = 16777216

Ответ: 16777216 цветов

Какой объём на диске (в Мбайтах) будет занимать 16-цветное изображение размером 2048х1024 пикселей?

I = K x i = 2048 x1024 x 4 = 2 1 x2 10 x2 10 x2 2 =2 23 бит = 1Мб

1 . Какой объём памяти (в Кбайтах) нужен для сохранения растрового изображения размером 64х256 пикселей при условии, что в изображении используется 4 цвета.

2. Скольких различных цветов могут быть пиксели растрового изображения, имеющего размер 1024х256 пикселей и занимающего на диске 160 килобайт?

Дискретное представление звуковой информации

Звук представляет собой звуковую волну с непрерывно меняющейся амплитудой и частотой.

Чем больше амплитуда сигнала, тем он громче для человека, чем больше частота сигнала, тем выше тон.

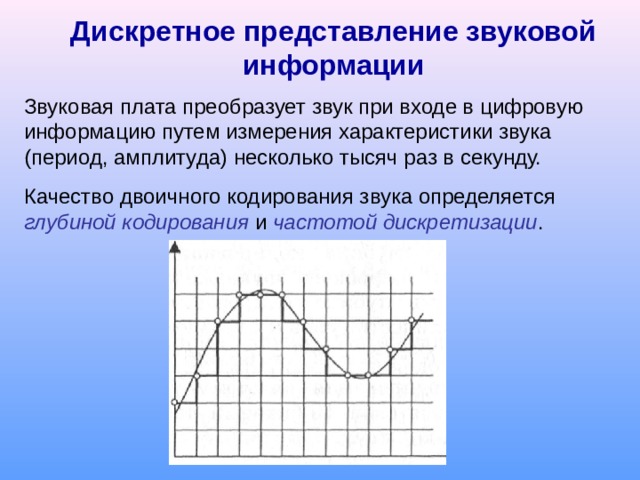
Дискретное представление звуковой информации

Звуковая плата преобразует звук при входе в цифровую информацию путем измерения характеристики звука (период, амплитуда) несколько тысяч раз в секунду.

Качество двоичного кодирования звука определяется глубиной кодирования и частотой дискретизации .

Дискретное представление звуковой информации

Частота дискретизации ( f ) – количество измерений уровня сигнала в единицу времени.

Частота дискретизации измеряется в герцах ( Гц ) и килогерцах ( кГц ). 1 кГц = 1000 Гц . Частота дискретизации, равная 100 Гц означает, что за одну секунду проводилось 100 измерений громкости звука.

Глубина кодирования или разрешение ( i ) — число разрядов, используемое для создания цифрового звука, —

Информационный объем звукозаписи

Размер цифрового аудиофайла ( I ) измеряется по формуле:

I – размер файла (в битах)

K — количество каналов записи (1 – моно, 2 – стерео)

f – частота дискретизации (в герцах )

i – разрешение, т.е. число бит, используемых для хранения каждого измеренного значения;

t – продолжительность звукового фрагмента (в секундах).

Определить размер (в байтах) цифрового моноаудиофайла, время звучания которого составляет 10 секунд при частоте дискретизации 22,05 кГц и разрешении 8 бит.

I = 1 x 2205 0 x 8 x 10 = 1764000 бит = 220500 байт

1 . Определите информационный объём стереоаудиофайла длительностью звучания 1 минута, если глубина кодирования 16 бит, а частота дискретизации 48 кГц.

2. Определить объем памяти для хранения цифрового моноаудиофайла, время звучания которого составляет две минуты при частоте дискретизации 44,1 кГц и разрешении 16 бит.

Источник