Дискретному способу представления информации примеры

Здравствуйте! Меня зовут Александр Георгиевич, и я являюсь вашим информационным гидом в области информационных технологий.

Если у вас возникли какие-либо недопонимания с такой темой, как «Дискретная форма представления информации», то записывайтесь ко мне на пробный индивидуальный урок по информатике и ИКТ.

В данной статье поговорим об аналоговом и дискретном процессе. Для глубоко понимания того, как кодируется различная информация, в обязательном порядке нужно разобраться с понятием дискретизации информации.

Настоятельно рекомендую вам, если решите записаться ко мне на частную подготовку, выбрать дистанционную форму обучения. Это очень удобно, недорого и крайне эффективно.

Пример аналогового процесса

Рассмотрим конкретный пример аналогового процесса, имеющий место быть в нашей повседневной жизни. Допустим, что проходят соревнования по кольцевым автогонкам на специальных гоночных автомобилях, называемых болидами.

Инженеры Формулы-$1$ построили зависимость, которая отражает скорость движения среднестатистического болида от времени.

Аналоговая форма представления информации

По оси абсцисс откладывается текущее время, измеряемое в секундах, а по оси ординат откладывается текущая скорость болида, измеряемая в километрах в час. Как видно из данного графика, общее время, затрачиваемое гоночной машины на проезд по кругу трассы, составляет ровно $90$ секунд.

Возникает закономерный следующий вопрос. Наш болид двигается по трассе постоянно или делает паузы, то есть рывками? Конечно, гоночная машина совершает свое движение в каждый момент времени, пока находится на трассе, то есть движение болида можно считать непрерывным процессом.

Давайте посмотрим на скорость, которую достигает болид в процессе движения. Очевидно, что скорость автомашины Формулы-$1$ не может принимать отрицательные значения. Минимальное значение скорости равно нулю, когда болид стоит на месте, не двигается.

Максимальное значение машины можно получить, «прочитав» предложенный график функции. За все время своего движения болид имел пиковую, максимальную скорость на $60$-ой секунде, и она составляла $310$ км/час. То есть в данном случае диапазон скорости, которую может принимать болид, равен $0-310$ км/час.

Как мы ранее рассмотрели, гоночная автомашина производит движение в каждый момент временного континуума, а, следовательно, и скорость ее также будет иметь строго детерминированное, то есть определенное значение в любой промежуток времени.

Аналоговый процесс или аналоговая форма представления информации – такое представление, в котором некая физическая величина принимает абсолютно любое значение из строго определенного диапазона, причем ее значения могут меняться непрерывно.

В нашем предметном случае физической величиной выступает скорость автомашины Формулы-$1$. Скорость болида может принимать любое значение из диапазона от $0$ до $310$ км/час. А величина скорости, как видно из графика, в самом грубом приближении меняется каждую долю секунды. А сам график можно считать аналоговой формой представления информации.

Приведу еще примеры аналоговых процессов:

построение в графическом виде зависимости между температурой окружающей среды и днем года, в который был произведен данный замер;

визуализация зависимости между громкостью речи, произносимой человеком, и временем, в течение которого человек говорил текст.

В аналоговых системах, как правило, происходит очень плавное изменение ее параметров, не наблюдается каких-либо скачков, рывков.

Что такое дискретная информация

В самом грубом приближении процессор персонального компьютера не способен обрабатывать ничего, кроме всевозможных комбинаций двух значений — $0$ и $1$. Система счисления, оперирующая алфавитом, содержащим лишь два различных значения, называется двоичной.

Двоичная система счисления и дискретная форма представления информации очень сильно взаимосвязаны между собой.

Давайте обратимся вновь к графику, на котором показана зависимость скорости болида от времени. Как мы поняли, компьютер не сможет «переварить» значения скорости, равные, например, $0$, $95$, $160$, да и вообще любые другие.

Вот здесь и приходит на помощь дискретная форма представления информации.

Вообще словосочетание «дискретная информация» означает то, что это прерывная информация.

Следовательно, нам нужно получить из аналоговой системы дискретную систему, а для этого придется непрерывную систему раздробить на несколько участков, фрагментов.

Давайте получим значения скорости машины Формулы-$1$ из графика, производя замеры каждые $10$ секунд. И построим точечный график функции на основе полученных данных.

Дискретная форма представления информации

Необходимо очень четко понимать, почему в данном случае был изображен точечный график, то есть точки-данные не соединены плавной сглаживающей линией.

Это связано с тем, что мы не знаем, какие значения принимает скорость болида, когда время не кратно десяти. Например, мы не проводили замеров на $11$, $24$ или $73$ секунде, следовательно, чему равняется скорость машины в этот времени, неизвестно.

Итак, мы произвели $8$ замеров (замер скорости на $0$ секунде и $90$ секунде бессмысленен, так как в этот момент временного континуума автогоночный автомобиль находится в состоянии покоя, и его скорость равна $0$):

Время, сек	$10$	$20$	$30$	$40$	$50$	$60$	$70$	$80$
Скорость, км/час	$95$	$100$	$190$	$200$	$285$	$310$	$175$	$80$

Подобную информацию персональный компьютер уже способен хранить, обрабатывать, передавать, копировать, переносить.

Только не нужно забывать, что мы должны работать в двоичной системе счисления, а для этого значения скорости, выраженные десятичными числами, необходимо перевести в бинарные значения, которые будут состоять исключительно из $0$ и $1$.

Осуществляем преобразование величин из десятичной системы счисления в бинарную систему:

Десятичное число	$95$	$100$	$190$	$200$	$285$	$310$	$175$	$80$
Двоичное число	$101111$	$1100100$	$10111110$	$11001000$	$100011101$	$100110110$	$10101111$	$101000$

По сути, мы представили исходную аналоговую информацию, заданную графиком функции, в дискретной форме представления информации.

Дискретная форма представления информации – такое представление, в котором физическая величина принимает конечное множество значений, причем ее величина изменяется скачкообразно.

Возвращаясь к нашему примеру необходимо понимать, что мы преобразовали заданную аналоговую систему (графическую зависимость скорости от времени) в дискретную систему, которая характеризуется $8$ двоичными числами.

А теперь мы попытаемся из дискретной системы восстановить аналоговую.

Итак, наш компьютер сохранил $8$ бинарных чисел, и теперь настало время восстановить информацию и построить на основе ее график зависимости скорости болида от текущего времени.

То есть представьте, что у вас в распоряжении есть $8$ двоичных чисел, которые выражают скорость машины Формулы-$1$ с шагом времени, равном $10$ секунд, и вы хотите построить некую графическую зависимость.

Восстановление аналогового процесса

И настал момент истины! Теперь можно сравнить точность преобразования информации из аналоговой формы в дискретную форму.

Видно, что аналоговый график, восстановленный из дискретных данных (изображение слева), не точно отражает исходную аналоговую модель (изображение справа).

С чем это связано?! В $1$-ую очередь с количеством замеров. Мы производили замеры каждые $10$ секунд и получили погрешность. Чтобы добиться полного соответствия, нам нужно производить замеры как можно чаще.

В современных системах специальные устройства производят замеры исследуемой величины несколько тысяч раз за секунду. А вообще, в теории информатики, процесс замера чего-либо аналогового называют частотой дискретизации.

Если мы провели замеры скорости хотя бы с периодичностью $0.1$ секунды, то получили бы практически идеальные вычисления с точки зрения дискретной формы представления информации. Тогда бы наши графики функции совпали на $99.9\%$.

Дискретная форма представления числовой, текстовой, графической, звуковой и видеоинформации

Информационные технологии за столь короткий период своего существования получили масштабное развитие. Человек научил персональный компьютер кодировать, то есть представлять в дискретной форме следующие виды информации:

Необходимо понимать, что в процессе перевода информации на дискретные «рельсы» всегда будет происходить искажение информации.

Чтобы минимизировать девиации, то есть отклонения в вычислениях, необходимо как можно чаще производить замеры исследуемой величины, т е повышать частоту дискретизации.

Обязательно познакомьтесь с дискретными формами приведенных выше видов информации, т к на официальном экзамене ЕГЭ по информатике и ИКТ может попасться любая из них.

На самом деле видов информации гораздо больше, чем было перечислено выше! Существует еще тактильная, вкусовая и обонятельная информация. Кстати, далеко не все виды информации можно представить в дискретной форме.

Остались вопросы по данной теме?

Если после прочтения данного материала вам что-то непонятно, то прошу ко мне на индивидуальную консультацию. Также можете задать дополнительные уточняющие вопросы в комментариях.

Тему «Дискретная форма представления информации» я считаю базовой и обязательной для детального изучения. Не поняв принцип дискретизации, очень сложно будет разбираться с тем, как происходит кодирование различных видов информации.

Также не пожалейте буквально $2-3$ минуты собственного времени и познакомьтесь с отзывами учеников, прошедших подготовку под моим началом. Все они добились поставленных целей за разумное время.

Источник

Дискретному способу представления информации примеры

Код ОГЭ: 1.1.3 Дискретная форма представления информации. Единицы измерения количества информации

Информация может быть представлена в аналоговой или дискретной форме. Величина в аналоговой форме может принимать бесконечное множество значений. Примерами аналогового представления информации могут служить звук скрипки, картина художника, показатели температуры воздуха, уровня воды в реке.

Величина в дискретной форме может принимать только конечное множество значений. Примеры дискретного представления информации: цифровые показания часов или спидометра, текст в книге, изображение на экране монитора.

Величину в аналоговой форме представления информации можно преобразовать в величину в дискретной форме. Этот процесс называется дискретизацией.

Представление информации в компьютере дискретно . В процессах хранения, обработки и передачи информации в компьютере используется двоичная знаковая система. Ее алфавит состоит всего из двух знаков <0, 1>. Для удобства использования такого алфавита договорились называть любой из его знаков бит (от англ. bit — binary digit — двоичный знак). Поскольку один бит может принимать только одно из двух значений, то им выражают одно из двух взаимоисключающих понятий: да/нет, истина/ложь, включено/выключено.

Способ представления информации с помощью кода из двух знаков оказался наиболее значимым для развития техники. Двоичные числа удобно хранить, обрабатывать и передавать с помощью электронных устройств. Основным носителем информации в них являются элементы, которые могут находиться в одном из двух состояний: включено/выключено, высокий/низкий уровень напряжения или тока, наличие/отсутствие намагниченности материалов. Условно одно состояние обозначают через 1, а другое через 0. Каждый такой элемент способен хранить один двоичный разряд, или бит информации.

Любое информационное сообщение представляется последовательностью нулей и единиц (цифрового кода). Этот метод представления информации называется двоичным кодированием. Таким образом, двоичный код является универсальным средством кодирования информации. Благодаря двоичному кодированию все действия по обработке сообщений компьютером сводятся к совокупности простых действий над 0 и 1.

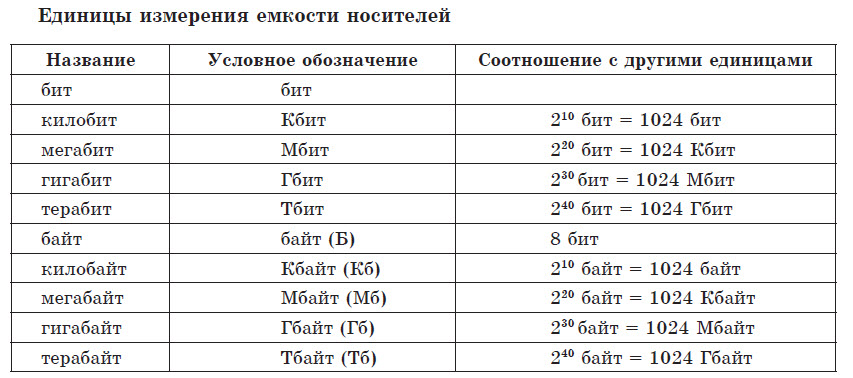
Единицы измерения количества информации

Основной единицей хранения и обработки цифровой информации принят байт.

Соответственно, с помощью одного байта можно получить 256 (= 2 8 ) двоичных значений (от 00000000 до 11111111). В современных персональных компьютерах байт является наименьшей совокупностью битов, которую компьютер обрабатывает одномоментно.

На практике применяют более емкие, чем байт, единицы измерения объема сообщений и емкости носителей — килобайты, мегабайты, гигабайты, терабайты. Множителем при переходе к более емкой единице измерения выступает число 1024 (= 2 10 ).

Системы счисления

Система счисления — совокупность обозначений, приемов и правил для записи чисел цифровыми знаками. В зависимости от способов изображения чисел цифрами системы счисления делятся на непозиционные и позиционные.

Непозиционные системы счисления — такие, в которых количественное значение каждой цифры не зависит от занимаемой ею позиции в изображении числа.

Примером может служить египетская система счисления — в ней иероглифы (цифры), составляющие число, можно записывать сверху вниз, справа налево или вперемежку. Значение числа равно сумме значений цифр в его записи.

Переходной от непозиционных систем к позиционным служит римская система счисления. В ней позиция некоторых цифр уже меняет значение числа: например, в числе IX единицу нужно отнять от десяти, а в числе XI единицу нужно прибавить к десяти. Однако количественное значение самих цифр Х и I от их позиции не зависит.

В римской системе цифры записываются слева направо в порядке убывания, и тогда их значения складываются. Если слева записана меньшая цифра, а справа — большая, то их значения вычитаются. Нежелательно записывать более трех одинаковых цифр подряд.

Например, для представления числа 348 в римской системе счисления надо выписать сначала число сотен, затем десятков и единиц: 300 — ССС, 40 — ХL, 8 — VIII. Затем соединить эти записи: CCCXLVIII. Аналогично для числа 1977: 1 тысяча — М, 900 — СМ, 70 — LXХ, 7 — VII. Результат: MCMLXXVII.

В непозиционных системах очень трудно производить многие действия над числами, особенно умножение и деление, слишком громоздка запись для больших чисел. Поэтому широкое распространение получили позиционные системы счисления.

Позиционные системы счисления — такие, в которых количественное значение каждой цифры зависит от ее позиции в числе.

Количество знаков (цифр), используемых для изображения числа, называется основанием системы счисления (или мощностью алфавита). Систему с основанием 10 называют десятичной, с основанием 2 — двоичной, с основанием 16 — шестнадцатеричной, в общем случае: с основанием k — k-ичной.

Место цифры в числе называется разрядом, а количество цифр в числе — его разрядностью. Разряды целого числа нумеруются справа налево начиная с 0. Дробные разряды нумеруют слева направо начиная с -1.

Примером позиционной системы счисления является используемая нами арабская десятичная система счисления. Иногда ее называют индо-арабской, поскольку она была придумана в Индии, а стала известна в Европе из арабских трактатов. Алфавит этой системы составляют 10 цифр — от 0 до 9. Каждая цифра в числе при перемещении справа налево в следующий разряд увеличивает свое значение в 10 раз. Чтобы определить значение числа, надо сложить произведения каждой его цифры на 10 в степени, равной разряду этого числа.

348 = 3 • 10 2 + 4 • 10 1 + 8 • 10 0

–348,17 = –(3 • 10 2 + 4 • 10 1 + 8 • 10 0 + 1 • 10 –1 + 7 • 10 –2 )

Системы счисления могут иметь различные основания. Чтобы различать, в какой системе счисления записано число, принято указывать ее основание в виде нижнего индекса справа от числа. Сам индекс всегда представляется в десятичной системе. Для самой десятичной системы индекс указывают только тогда, когда используется какая–либо другая система:

316 — число в десятичной системе счисления,
316₈ — число в восьмеричной системе счисления.

Свойства записи чисел в позиционной системе счисления:

Для записи чисел в позиционной системе счисления с основанием k требуется k знаков (алфавит системы состоит из k цифр или букв).
Основание системы счисления, записанное в ней, всегда имеет вид 10 (читается «один ноль»).
С помощью n разрядов в позиционной системе счисления с основанием k могут быть записаны k n чисел (от 0 до k n–1 ).

Если основание системы k больше 10, то цифры старше 10 при записи обозначают прописными буквами латинского алфавита: A, B, …, Z. При этом цифре 10 соответствует знак A, цифре 11 — знак B и т. д.

Информация в компьютере представлена в цифровой двоичной форме. В целях экономичного отображения двоичную информацию можно представлять в шестнадцатеричном виде. В программировании часто используется восьмеричная запись чисел.

В общем виде число в позиционной системе счисления может быть представлено как последовательность символов алфавита (цифр), обозначенных через а₁, а₂, а₃ и т. д. Для числа А с количеством целых разрядов n и количеством дробных разрядов m запись имеет вид:

Такая запись называется свернутой записью числа. Эту форму записи мы используем в повседневной жизни, поэтому ее называют также естественной.

Представление числа в виде многочлена называют развернутой записью числа:

Развернутая запись числа задает правило для вычисления числа по его цифрам в k–ичной системе счисления. Для уменьшения количества вычислений пользуются схемой Горнера, которая получается путем поочередного выноса основания системы k за скобки:

Конспект урока по информатике «Дискретная форма представления информации».

Источник