Динамическое программирование это способ решения

Динамическое программирование

Динамическое программирование — это когда у нас есть задача, которую непонятно как решать, и мы разбиваем ее на меньшие задачи, которые тоже непонятно как решать. (с) А.Кумок

Содержание

Процесс разработки алгоритмов динамического программирования [ править ]

В процессе составления алгоритмов динамического программирования, требуется следовать последовательности из четырёх действий:

1. Описать структуру оптимального решения.
2. Рекурсивно определить значение оптимального решения.
3. Вычислить значение оптимального решения с помощью метода восходящего анализа.
4. Составить оптимальное решение на основе полученной информации.

Оптимальная подструктура [ править ]

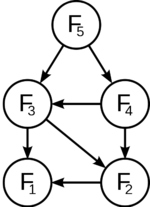
Наличие оптимальной подструктуры в задаче используется для определения применимости динамического программирования и жадных алгоритмов для решения оной. Например, задача по нахождению кратчайшего пути между некоторыми вершинами графа содержит в себе оптимальное решение подзадач.

Многие задачи, решаемые динамическим программированием, можно определить как поиск в заданном ориентированном ациклическом графе кратчайшего пути от одной вершины к другой.

Отсутствие оптимальной подструктуры [ править ]

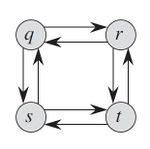
Иногда оптимальная подструктура может отсутствовать в задаче. Рассмотрим задачу, в которой имеется ориентированный граф $G = (V, E)$ и вершины $u, v \in V$, задачу по определению простого пути от вершины $u$ к вершине $v$, состоящий из максимального количества рёбер.

Рассмотрим путь $q \rightarrow r \rightarrow t$, который является самым длинным простым путем $q \rightsquigarrow t$. Является ли путь $q \rightarrow r$ самым длинным путем $q \rightsquigarrow r$? Нет, поскольку простой путь $q \rightarrow s \rightarrow t \rightarrow r$ длиннее. Является ли путь $r \rightarrow t$ самым длинным путем $r \rightsquigarrow t$? Снова нет, поскольку простой путь $r \rightarrow q \rightarrow s \rightarrow t$ длиннее. Таким образом, в задаче о поиске самого длинного невзвешенного пути не возникает никаких оптимальных подструктур. Для этой задачи до сих пор не найдено ни одного эффективного алгоритма, работающего по принципу динамического программирования. Фактически, это NP-полная задача, т.е. вряд ли ее можно решить в течение полиномиального времени.

Оптимальность для подзадач [ править ]

Важнейшее свойство задач, которое позволяет решать их с помощью динамического программирования, это оптимальность для подзадач. В зависимости от формулировки задачи, будь то динамическое программирование на отрезке, на префиксе, на дереве, термин оптимальности для подзадач может быть различным, но, в целом, формулируется так: если есть оптимальное решение для некоторой подзадачи, которая возникает в процессе решения задачи, то именно его нужно использовать для решения задачи в целом.

Принцип оптимальности на префиксе [ править ]

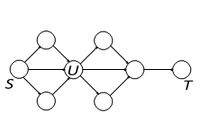
Рассмотрим некий необратимый процесс производства и представим его в виде ориентированного и ациклического графа. Процесс проходит некий ряд состояний. Началом производства (первым состоянием) обозначим вершину графа $S$, а конец производства (последнее состояние) $T$. Процесс требует оптимизации, т.е. требуется найти оптимальный путь $S \rightsquigarrow T$. Он проходит через вершину графа $U$. Префикс оптимального пути $S \rightsquigarrow U$ является оптимальным путём $S \rightsquigarrow U$. Теперь рассмотрим принцип оптимальности для динамического программирования на префиксе. Итак, имеем некоторый оптимальный путь $S \rightsquigarrow T$, который проходит через $U$. Пусть префикс $ \Delta U$, т.е. путь от $S \rightsquigarrow U$, неоптимален. Тогда заменим неоптимальную часть $S \rightsquigarrow U$ пути $S \rightsquigarrow T$ оптимальной, а путь $U \rightsquigarrow T$ добавим в конец. Получим оптимальный путь $S \rightsquigarrow T$. Принцип оптимальности для подзадач выполняется. Т.е. чтобы получить оптимальный путь из одной вершины графа в другую, префиксы меньших путей должны быть оптимальными.

В качестве примера рассмотрим следующую задачу: пусть дан ациклический ориентированный взвешенный граф, требуется найти вес кратчайшего пути из u в v. Воспользуемся принципом оптимальности на префиксе.
Пусть [math]d[/math] — функция, где [math]d(i)[/math] — вес кратчайшего пути из [math]u[/math] в [math]i[/math] . Ясно, что [math]d(u)[/math] равен [math]0[/math] . Пусть [math]w(i, j)[/math] — вес ребра из [math]i[/math] в [math]j[/math] . Будем обходить граф в порядке топологической сортировки. Получаем следующие соотношения:

Так как мы обходим граф в порядке топологической сортировки, то на [math]i[/math] -ом шаге всем [math]d(j)[/math] ( [math]j[/math] такие, что существует ребро из [math]j[/math] в [math]i[/math] ) уже присвоены оптимальные ответы, и, следовательно, [math]d(i)[/math] также будет присвоен оптимальный ответ.

Примеры задач [ править ]

Принцип оптимальности на подотрезках [ править ]

Требуется посчитать функцию $f(1, n)$. Принцип состоит в следующем: пусть для всех отрезков $i$, $j$ (где [math] u \leqslant i \leqslant j \leqslant v [/math] ) известен оптимальный ответ для функции $f(i, j)$. Тогда мы будем вычислять $f(u, v)$ через такие $f(i, j)$. В качестве примера рассмотрим следующую классическую задачу: дана строка длины n, нужно найти максимальный подпалиндром (подпоследовательность максимальной длины, которая является палиндромом). Пусть $d(i, j)$ — ответ на задачу для подстроки, начинающаяся с символа $i$ и заканчивающаяся в символе $j$. Ясно, что $d(i, j) = 0$ для всех $i, j,$ таких что $i > j$ и $d(i, i) = 1$ для всех $i$. Пусть нам нужно посчитать значение для $d(i, j)$, причем значение $d$ для всех $l, r$, таких что [math] i \leqslant l \leqslant r \leqslant j [/math] уже посчитаны и они оптимальны. Рассмотрим два случая:

1. [math] s(i) \neq s(j) [/math] , тогда [math] d(i, j) = \max(d(i, j — 1), d(i + 1, j)) [/math]
2. [math] s(i) = s(j) [/math] , тогда [math] d(i, j) = d(i + 1, j — 1) + 2 [/math]

1. Так [math]s(i) \neq s(j)[/math] , символы $s(i)$ и $s(j)$ не могут входить в максимальный подпалиндром одновременно, то есть либо $s(i)$ входят в максимальный подпалиндром(тогда его длина $d[i, j — 1]$), либо $s(j)$ входит в максимальный подпалиндром (тогда его длина $d[i + 1, j]$), либо оба не входят в максимальный подпалиндром (тогда его длина $= d[i, j — 1] = d[i + 1, j]$).
2. Данное равенство следует из факта, что выгодно включить в максимальный подпалиндром символы $s(i)$ и $s(j)$.

Примеры задач [ править ]

Принцип оптимальности на подмножествах [ править ]

Требуется посчитать функцию [math]f(A)[/math] , где [math]A[/math] — некоторое множество. Принцип состоит в следующем: пусть для всех множеств [math]B[/math] (где [math]B \in A[/math] ) известен оптимальный ответ для функции [math]f(B)[/math] . Тогда будем вычислять [math]f(A)[/math] через такие [math]f(B)[/math] . В качестве примера рассмотрим задачу о коммивояжере.

Обозначим [math]d[i][mask][/math] как наименьшую стоимость пути из вершины [math]i[/math] в вершину [math]0[/math] , проходящую (не считая вершины [math]i[/math] ) единожды по всем тем и только тем вершинам [math]j[/math] , для которых [math]mask_j = 1[/math] (т.е. [math]d[i][mask][/math] уже найденный оптимальный путь от [math]i[/math] -ой вершины до [math]0[/math] -ой, проходящий через те вершины, где [math]mask_j=1[/math] . Если [math]mask_j=0[/math] ,то эти вершины еще не посещены). Тогда воспользуемся принципом оптимальности на подмножествах. Стоимостью минимального гамильтонова цикла в исходном графе будет значение [math] d[0][2^n-1][/math] — стоимость пути из [math]0[/math] -й вершины в [math]0[/math] -ю, при необходимости посетить все вершины.

Примеры задач [ править ]

Мемоизация [ править ]

Определение:

Мемоизация (англ. memoization) — сохранение результатов выполнения функций для предотвращения повторных вычислений.

Это один из способов оптимизации, применяемый для увеличения скорости выполнения компьютерных программ. Перед вызовом функции проверяется, вызывалась ли функция ранее:

• если не вызывалась, функция вызывается и результат её выполнения сохраняется;
• если вызывалась, используется сохранённый результат.

В качестве примера рассмотрим задачу о нахождении числа Фибоначчи под номером [math]n[/math] . Без мемоизации:

Источник

Динамическое программирование. Классические задачи

Здравствуй, Хабрахабр. В настоящий момент я работаю над учебным пособием по олимпиадному программированию, один из параграфов которого посвящен динамическому программированию. Ниже приведена выдержка из данного параграфа. Пытаясь объяснить данную тему как можно проще, я постарался сложные моменты сопроводить иллюстрациями. Мне интересно ваше мнение о том, насколько понятным получился данный материал. Также буду рад советам, какие еще задачи стоит включить в данный раздел.

Во многих олимпиадных задачах по программированию решение с помощью рекурсии или полного перебора требует выполнения очень большого числа операций. Попытка решить такие задачи, например, полным перебором, приводит к превышению времени выполнения.

Однако среди переборных и некоторых других задач можно выделить класс задач, обладающих одним хорошим свойством: имея решения некоторых подзадач (например, для меньшего числа n), можно практически без перебора найти решение исходной задачи.

Такие задачи решают методом динамического программирования, а под самим динамическим программированием понимают сведение задачи к подзадачам.

Последовательности

Классической задачей на последовательности является следующая.

Один из способов решения, который может показаться логичным и эффективным, — решение с помощью рекурсии:

Используя такую функцию, мы будем решать задачу «с конца» — будем шаг за шагом уменьшать n, пока не дойдем до известных значений.

Но как можно заметить, такая, казалось бы, простая программа уже при n = 40 работает заметно долго. Это связано с тем, что одни и те же промежуточные данные вычисляются по несколько раз — число операций нарастает с той же скоростью, с какой растут числа Фибоначчи — экспоненциально.

Один из выходов из данной ситуации — сохранение уже найденных промежуточных результатов с целью их повторного использования:

Приведенное решение является корректным и эффективным. Но для данной задачи применимо и более простое решение:

Такое решение можно назвать решением «с начала» — мы первым делом заполняем известные значения, затем находим первое неизвестное значение (F₃), потом следующее и т.д., пока не дойдем до нужного.

Именно такое решение и является классическим для динамического программирования: мы сначала решили все подзадачи (нашли все F_i для i 2, соответственно.

Следующая задача одномерного динамического программирования встречается в различных вариациях.

Задача 1. Посчитать число последовательностей нулей и единиц длины n, в которых не встречаются две идущие подряд единицы.

При n 2. То есть данная задача фактически сводится к нахождению чисел Фибоначчи.

Двумерное динамическое программирование

Классической задачей двумерного динамического программирования является задача о маршрутах на прямоугольном поле.
В разных формулировках необходимо посчитать число маршрутов или найти маршрут, который является лучшим в некотором смысле.

Приведем пару формулировок таких задач:

Задача 2. Дано прямоугольное поле размером n*m клеток. Можно совершать шаги длиной в одну клетку вправо или вниз. Посчитать, сколькими способами можно попасть из левой верхней клетки в правую нижнюю.

Задача 3. Дано прямоугольное поле размером n*m клеток. Можно совершать шаги длиной в одну клетку вправо, вниз или по диагонали вправо-вниз. В каждой клетке записано некоторое натуральное число. Необходимо попасть из верхней левой клетки в правую нижнюю. Вес маршрута вычисляется как сумма чисел со всех посещенных клеток. Необходимо найти маршрут с минимальным весом.

Для всех таких задач характерным является то, что каждый отдельный маршрут не может пройти два или более раз по одной и той же клетке.

Рассмотрим более подробно задачу 2. В некоторую клетку с координатами (i,j) можно прийти только сверху или слева, то есть из клеток с координатами (i – 1, j) и (i, j – 1):

Таким образом, для клетки (i, j) число маршрутов A[i][j] будет равно
A[i – 1][j] + A[i][j – 1], то есть задача сводится к двум подзадачам. В данной реализации используется два параметра — i и j — поэтому применительно к данной задаче мы говорим о двумерном динамическом программировании.

Теперь мы можем пройти последовательно по строкам (или по столбцам) массива A, находя число маршрутов для текущей клетки по приведенной выше формуле. Предварительно в A[0][0] необходимо поместить число 1.

В задаче 3 в клетку с координатами (i, j) мы можем попасть из клеток с координатами
(i – 1, j), (i, j – 1) и (i – 1, j – 1). Допустим, что для каждой из этих трех клеток мы уже нашли маршрут минимального веса, а сами веса поместили в W[i – 1][j], W[i][j – 1],
W[i – 1][j – 1]. Чтобы найти минимальный вес для (i, j), необходимо выбрать минимальный из весов W[i – 1][j], W[i][j – 1], W[i – 1][j – 1] и прибавить к нему число, записанное в текущей клетке:

W[i][j] = min(W[i–1][j], W[i][j – 1], W[i – 1][j – 1]) + A[i][j];

Данная задача осложнена тем, что необходимо найти не только минимальный вес, но и сам маршрут. Поэтому в другой массив мы дополнительно для каждой клетки будем записывать, с какой стороны в нее надо попасть.

На следующем рисунке приведен пример исходных данных и одного из шагов алгоритма.

В каждую из уже пройденных клеток ведет ровно одна стрелка. Эта стрелка показывает, с какой стороны необходимо прийти в эту клетку, чтобы получить минимальный вес, записанный в клетке.

После прохождения всего массива необходимо будет проследить сам маршрут из последней клетки, следуя по стрелкам в обратную сторону.

Задачи на подпоследовательности

Рассмотрим задачу о возрастающей подпоследовательности.

Задача 4. Дана последовательность целых чисел. Необходимо найти ее самую длинную строго возрастающую подпоследовательность.

Начнем решать задачу с начала — будем искать ответ, начиная с первых членов данной последовательности. Для каждого номера i будем искать наибольшую возрастающую подпоследовательность, оканчивающуюся элементом в позиции i. Пусть исходная последовательность хранится в массиве A. В массиве L будем записывать длины максимальных подпоследовательностей, оканчивающихся текущим элементом. Пусть мы нашли все L[i] для 1

Источник