Дифференцированный способ погашения кредита задачи

Дифференцированный способ погашения кредита задачи

Решите задачи на дифференцированные платежи (задания ЕГЭ) Алексей взял кредит в банке на срок 17 месяцев. По договору Алексей должен вернуть кредит ежемесячными платежами. В конце каждого месяца к оставшейся сумме долга добавляется r % этой суммы и своим ежемесячным платежом Алексей погашает эти добавленные проценты и уменьшает сумму долга. Ежемесячные платежи подбираются так, чтобы долг уменьшался на одну и ту же величину каждый месяц. Известно, что общая сумма, выплаченная Алексеем банку за весь срок кредитования, оказалась на 27% больше, чем сумма, взятая им в кредит. Найдите r.

Пусть сумма кредита равна S. По условию долг Алексея должен уменьшаться до нуля равномерно:

К концу каждого месяца к сумме долга добавляется r%. Пусть Тогда последовательность сумм долга вместе с процентами такова:

Следовательно, выплаты должны быть следующими:

Всего следует выплатить:

Общая сумма выплат оказалась на 27% больше суммы, взятой в кредит, поэтому:

Откуда полeчаем, что

Ответ:

Решите задачи на дифференцированные платежи (задания ЕГЭ) Алексей взял кредит в банке на срок 12 месяцев. По договору Алексей должен вернуть кредит ежемесячными платежами. В конце каждого месяца к оставшейся сумме долга добавляется r % этой суммы и своим ежемесячным платежом Алексей погашает эти добавленные проценты и уменьшает сумму долга. Ежемесячные платежи подбираются так, чтобы долг уменьшался на одну и ту же величину каждый месяц. Известно, что общая сумма, выплаченная Алексеем банку за весь срок кредитования, оказалась на 13% больше, чем сумма, взятая им в кредит. Найдите r.

Ответ:

Аналоги к заданию № 3470: 3471 Все

Решите задачи на дифференцированные платежи (задания ЕГЭ) Сергей взял кредит в банке на срок 9 месяцев. В конце каждого месяца общая сумма оставшегося долга увеличивается на 12%, а затем уменьшается на сумму, уплаченную Сергеем. Суммы, выплачиваемые в конце каждого месяца, подбираются так, чтобы в результате сумма долга каждый месяц уменьшалась равномерно, то есть на одну и ту же величину. Сколько процентов от суммы кредита составила переплата (сумма, уплаченная сверх тела кредита)?.

Пусть сумма кредита S, переплата от суммы кредита x %.

Предложение «Суммы, выплачиваемые в конце каждого месяца, подбираются так, чтобы в результате сумма долга каждый месяц уменьшалась равномерно, то есть на одну и ту же величину» означает: Сергей взятую сумму возвращал в банк равными долями. Сумма, образованная применением процентной ставки, составляет:

Найдём значение процента переплаты от суммы кредита:

Ответ:

Решите задачи на дифференцированные платежи (задания ЕГЭ) Иван взял кредит в банке на срок 19 месяцев. В конце каждого месяца общая сумма оставшегося долга увеличивается на 15%, а затем уменьшается на сумму, уплаченную Иваном. Суммы, выплачиваемые в конце каждого месяца, подбираются так, чтобы в результате сумма долга каждый месяц уменьшалась равномерно, то есть на одну и ту же величину. Сколько процентов от суммы кредита составила переплата (сумма, уплаченная сверх тела кредита)?.

Ответ:

Аналоги к заданию № 3472: 3473 Все

Решите задачи на дифференцированные платежи (задания ЕГЭ) В июле планируется взять кредит в банке на сумму 9 млн рублей на целое число лет. Условия возврата таковы: каждый январь долг возрастает на 20% по сравнению с концом предыдущего года; с февраля по июнь каждого года необходимо вы-платить часть долга; в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года. Чему будет равна общая сумма выплат после полного погашения кредита, если наибольший годовой платёж составит 3,6 млн рублей?.

По условию долг уменьшается в арифметической прогрессии:

Первая выплата равна

Вторая выплата равна

Третья выплата равна

Четвертая выплата равна и так далее.

Значит, наибольшая выплата — первая, d = 1,8, то есть всего будет 5 выплат и они составляют арифметическую прогрессию с разностью

Общая выплата равна

Ответ:

Источник

Решение задачи про дифференцированный платеж в общем виде. Задание 17

В этой статье мы выведем общую формулу для решения экономических задач, условие которых предполагает погашение задолженности по кредиту с использованием дифференцированного платежа.

Дифференцированный платеж – это способ погашения кредита, при котором заемщиком выплачивается основная сумма займа («тело кредита») равными частями, а начисление процентов осуществляется только на остаток задолженности в каждый конкретный момент времени.

Если в задаче присутствуют слова «равными частями», или «долг уменьшается на одну и ту же величину» , то, скорее всего, речь идет о дифференцированном платеже.

Отметим, что в этом случае платежи отличаются между собой.

Внимание! Следует отличать эти задачи от тех, в которых долг отдается равными платежами.

Пусть заемщик взял в кредит 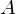рублей на лет при годовой процентной ставке, равной %.

В случае дифференцированного платежа ежегодный платеж состоит из двух частей и равен

1) — часть долга, выплачиваемая ежегодно. Это та составляющая ежегодной выплаты, которая остается постоянной.

2) Проценты на оставшуюся часть долга. Это составляющая ежегодного платежа, которая меняется с каждой выплатой и зависит от порядкового номера этой выплаты.

В первый год выплата процентов по кредиту равна ,

во второй —

в третий —

Выплата процентов по кредиту в — ый год равна .

Тогда общий платеж в первый год равен

Во второй:

В — ый:

Выплаты по процентам представляют собой убывающую арифметическую прогрессию, в которой

Суммарно выплаты по процентам равны:

Сумма слагаемых в скобках находится по формуле суммы членов арифметической прогрессии:

В итоге, если клиент берет в кредит 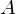рублей на лет при годовой процентной ставке, равной %, то при дифференцированном платеже он выплатит за лет всего

В этом случае переплата банку составляет рублей или процентов (считаем, сколько процентов составляет переплата от суммы долга, для этого сумму переплаты делим на сумму долга и умножаем на 100%).

Например, если клиент берет ипотеку на квартиру 10 млн руб. сроком на 20 лет под 10% годовых (фантастически низкий процент), то по истечении этого срока он заплатит за квартиру:

млн. руб. То есть сумму, более чем в два раза превышающую сумму кредита.

В июле пла­ни­ру­ет­ся взять кре­дит в банке на сумму 28 млн руб­лей на не­ко­то­рый срок (целое число лет). Усло­вия его воз­вра­та та­ко­вы:

— каж­дый ян­варь долг воз­рас­та­ет на 25% по срав­не­нию с кон­цом преды­ду­ще­го года;

— с фев­ра­ля по июнь каж­до­го года не­об­хо­ди­мо вы­пла­тить часть долга;

— в июле каж­до­го года долг дол­жен быть на одну и ту же сумму мень­ше долга на июль преды­ду­ще­го года.

Чему будет равна общая сумма вы­плат после пол­но­го по­га­ше­ния кре­ди­та, если наи­боль­ший го­до­вой платёж со­ста­вит 9 млн руб­лей?

По условию задачи процентная ставка % годовых.

Пусть кредит взят на лет. Наибольший годовой платеж будет в первый год, когда невыплаченный остаток максимальный, он равен сумме, взятой в кредит. Годовой платеж в первый год равен млн руб.

По условию наибольший годовой платеж равен 9 млн руб.

Следовательно, кредит взят на 14 лет.

Тогда общая сумма выплат равна млн руб.

Ответ: млн руб.

Источник