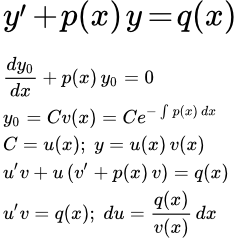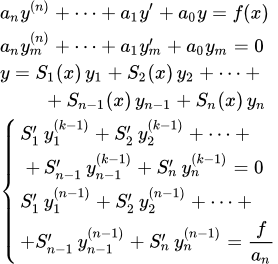Дифференциальные уравнения способ вариации постоянных

Метод Лагранжа (вариации постоянной). Линейные дифференциальные уравнения первого порядка.

Рассмотрим линейное неоднородное дифференциальное уравнение первого порядка:
(1) .
Существует три способа решения этого уравнения:

Рассмотрим решение линейного дифференциального уравнения первого порядка методом Лагранжа.

Метод вариации постоянной (Лагранжа)

В методе вариации постоянной мы решаем уравнение в два этапа. На первом этапе мы упрощаем исходное уравнение и решаем однородное уравнение. На втором этапе мы заменим постоянную интегрирования, полученную на первой стадии решения, на функцию. После чего ищем общее решение исходного уравнения.

Шаг 1 Решение однородного уравнения

Ищем решение однородного уравнения:

Это уравнение с разделяющимися переменными

Разделяем переменные — умножаем на dx , делим на y :

Интегрируем:

Интеграл по y — табличный:

Тогда

Потенцируем:

Заменим постоянную e C на C и уберем знак модуля, что сводится к умножению на постоянную ±1 , которую включим в C :

Шаг 2 Заменим постоянную C на функцию

Теперь заменим постоянную C на функцию от x :
C → u ( x )
То есть, будем искать решение исходного уравнения (1) в виде:
(2)
Находим производную.

По правилу дифференцирования сложной функции:
.
По правилу дифференцирования произведения:

.
Подставляем в исходное уравнение (1):
(1) ;

.
Два члена сокращаются:
;
.
Интегрируем:
.
Подставляем в (2):
.
В результате получаем общее решение линейного дифференциального уравнения первого порядка:
.

Пример решения линейного дифференциального уравнения первого порядка методом Лагранжа

Решаем однородное уравнение:

Разделяем переменные:

Умножим на :

Интегрируем:

Интегралы табличные:

Потенцируем:

Заменим постоянную e C на C и убираем знаки модуля:

Отсюда:

Заменим постоянную C на функцию от x :
C → u ( x )

Находим производную:
.
Подставляем в исходное уравнение:
;
;
Или:
;
.
Интегрируем:
;
Решение уравнения:
.

Общее решение уравнения:
.

Автор: Олег Одинцов . Опубликовано: 27-07-2012 Изменено: 01-03-2015

Источник

Метод вариации произвольной постоянной решения линейных неоднородных уравнений

Пример №1 . Найдём общее решение уравнения y» + 4y’ + 3y = 9e -3 x . Рассмотрим соответствующее однородное уравнение y» + 4y’ + 3y = 0. Корни его характеристического уравнения r 2 + 4r + 3 = 0 равны -1 и -3. Поэтому фундаментальная система решений однородного уравнения состоит из функций y₁ = e — x и y₂ = e -3 x . Решение неоднородного уравнения ищем в виде y = C₁(x)e — x + C₂(x)e -3 x . Для нахождения производных C’₁, C’₂ составляем систему уравнений (8)
C′₁·e -x +C′₂·e -3x =0
-C′₁·e -x -3C′₂·e -3x =9e -3x
решая которую, находим , Интегрируя полученные функции, имеем
Окончательно получим

Пример №2 . Решить линейные дифференциальные уравнения второго порядка с постоянными коэффициентами методом вариации произвольных постоянных:

y(0) =1 + 3ln3
y’(0) = 10ln3

Решение:
Данное дифференциальное уравнение относится к линейным дифференциальным уравнениям с постоянными коэффициентами.
Решение уравнения будем искать в виде y = e rx . Для этого составляем характеристическое уравнение линейного однородного дифференциального уравнения с постоянными коэффициентами:
r 2 -6 r + 8 = 0
D = (-6) 2 — 4·1·8 = 4

Корни характеристического уравнения: r₁ = 4, r₂ = 2
Следовательно, фундаментальную систему решений составляют функции: y₁=e 4x , y₂=e 2x
Общее решение однородного уравнения имеет вид: y =C₁·e 4x +C₂·e 2x
Поиск частного решения методом вариации произвольной постоянной.
Для нахождения производных C’_i составляем систему уравнений:
C′₁·e 4x +C′₂·e 2x =0
C′₁(4e 4x ) + C′₂(2e 2x ) = 4/(2+e -2x )
Выразим C’₁ из первого уравнения:
C’₁ = -c₂e -2x
и подставим во второе. В итоге получаем:
C’₁ = 2/(e 2x +2e 4x )
C’₂ = -2e 2x /(e 2x +2e 4x )
Интегрируем полученные функции C’_i:
C₁ = 2ln(e -2x +2) — e -2x + C * ₁
C₂ = ln(2e 2x +1) – 2x+ C * ₂

Поскольку y =C₁·e 4x +C₂·e 2x , то записываем полученные выражения в виде:
C₁ = (2ln(e -2x +2) — e -2x + C * ₁) e 4x = 2 e 4x ln(e -2x +2) — e 2x + C * ₁ e 4x
C₂ = (ln(2e 2x +1) – 2x+ C * ₂)e 2x = e 2x ln(2e 2x +1) – 2x e 2x + C * ₂ e 2x
Таким образом, общее решение дифференциального уравнения имеет вид:
y = 2 e 4x ln(e -2x +2) — e 2x + C * ₁ e 4x + e 2x ln(2e 2x +1) – 2x e 2x + C * ₂ e 2x
или
y = 2 e 4x ln(e -2x +2) — e 2x + e 2x ln(2e 2x +1) – 2x e 2x + C * ₁ e 4x + C * ₂ e 2x

Найдем частное решение при условии:
y(0) =1 + 3ln3
y’(0) = 10ln3

Подставляя x = 0, в найденное уравнение, получим:
y(0) = 2 ln(3) — 1 + ln(3) + C * ₁ + C * ₂ = 3 ln(3) — 1 + C * ₁ + C * ₂ = 1 + 3ln3
Находим первую производную от полученного общего решения:
y’ = 2e 2x (2C₁ e 2x + C₂ -2x +4 e 2x ln(e -2x +2)+ ln(2e 2x +1)-2)
Подставляя x = 0, получим:
y’(0) = 2(2C₁ + C₂ +4 ln(3)+ ln(3)-2) = 4C₁ + 2C₂ +10 ln(3) -4 = 10ln3

Получаем систему из двух уравнений:
3 ln(3) — 1 + C * ₁ + C * ₂ = 1 + 3ln3
4C₁ + 2C₂ +10 ln(3) -4 = 10ln3
или
C * ₁ + C * ₂ = 2
4C₁ + 2C₂ = 4
или
C * ₁ + C * ₂ = 2
2C₁ + C₂ = 2
Откуда: C₁ = 0, C * ₂ = 2
Частное решение запишется как:
y = 2e 4x ·ln(e -2x +2) — e 2x + e 2x ·ln(2e 2x +1) – 2x·e 2x + 2·e 2x

Источник

Решение линейных неоднородных дифференциальных уравнений высших порядков методом Лагранжа

Метод Лагранжа (вариация постоянных)

Рассмотрим линейное неоднородное дифференциальное уравнение с постоянными коэффициентами произвольного n-го порядка:
(1) .
Метод вариации постоянной, рассмотренный нами для уравнения первого порядка, также применим и для уравнений более высоких порядков.

Решение выполняется в два этапа. На первом этапе мы отбрасываем правую часть и решаем однородное уравнение. В результате получаем решение, содержащее n произвольных постоянных. На втором этапе мы варьируем постоянные. То есть мы считаем, что эти постоянные являются функциями от независимой переменной x и находим вид этих функций.

Хотя мы здесь рассматриваем уравнения с постоянными коэффициентами, но метод Лагранжа также применим и для решения любых линейных неоднородных уравнений. Для этого, однако, должна быть известна фундаментальная система решений однородного уравнения.

Шаг 1. Решение однородного уравнения

Как и в случае уравнений первого порядка, вначале мы ищем общее решение однородного уравнения, приравнивая правую неоднородную часть к нулю:
(2) .
Общее решение такого уравнения имеет вид:
(3) .
Здесь – произвольные постоянные; – n линейно независимых решений однородного уравнения (2), которые образуют фундаментальную систему решений этого уравнения.

Шаг 2. Вариация постоянных – замена постоянных функциями

На втором этапе мы займемся вариацией постоянных. Другими словами, мы заменим постоянные на функции от независимой переменной x :
.
То есть мы ищем решение исходного уравнения (1) в следующем виде:
(4) .

Если мы подставим (4) в (1), то получим одно дифференциальное уравнение для n функций . При этом мы можем связать эти функции дополнительными уравнениями. Тогда получится n уравнений, из которых можно определить n функций . Дополнительные уравнения можно составить различными способами. Но мы это сделаем так, чтобы решение имело наиболее простой вид. Для этого, при дифференцировании, нужно приравнивать к нулю члены, содержащие производные от функций . Продемонстрируем это.

Чтобы подставить предполагаемое решение (4) в исходное уравнение (1), нам нужно найти производные первых n порядков от функции, записанной в виде (4). Дифференцируем (4), применяя правила дифференцирования суммы и произведения:
.
Сгруппируем члены. Сначала выпишем члены с производными от , а затем – члены с производными от :

.
Наложим на функции первое условие:
(5.1) .
Тогда выражение для первой производной по будет иметь более простой вид:
(6.1) .

Тем же способом находим вторую производную:

.
Наложим на функции второе условие:
(5.2) .
Тогда
(6.2) .
И так далее. В дополнительных условиях, мы приравниваем члены, содержащие производные функций , к нулю.

Таким образом, если выбрать следующие дополнительные уравнения для функций :
(5.k) ,
то первые производных по будут иметь наиболее простой вид:
(6.k) .
Здесь .

Подставляем в исходное уравнение (1):
(1) ;

.
Учтем, что все функции удовлетворяют уравнению (2):
.
Тогда сумма членов, содержащих дают нуль. В итоге получаем:
(7) .

В результате мы получили систему линейных уравнений для производных :
(5.1) ;
(5.2) ;
(5.3) ;
. . . . . . .
(5.n-1) ;
(7′) .

Решая эту систему, находим выражения для производных как функции от x . Интегрируя, получим:
.
Здесь – уже не зависящие от x постоянные. Подставляя в (4), получаем общее решение исходного уравнения.

Заметим, что для определения величин производных мы нигде не использовали тот факт, что коэффициенты a_i являются постоянными. Поэтому метод Лагранжа применим для решения любых линейных неоднородных уравнений, если известна фундаментальная система решений однородного уравнения (2).

Далее рассмотрены примеры решения уравнений методом Лагранжа.

Примеры

Решить уравнения методом вариации постоянных (Лагранжа).

Решение примеров > > >

Автор: Олег Одинцов . Опубликовано: 05-08-2013 Изменено: 22-06-2017

Источник

Дифференциальные уравнения способ вариации постоянных

Линейное неоднородное уравнение второго порядка с переменными коэффициентами имеет вид \[y» + \left( x \right)y’ + \left( x \right)y = f\left( x \right),\] где \(\left( x \right),\) \(\left( x \right)\) и \(f\left( x \right)\) − непрерывные функции на отрезке \(\left[ \right].\)

Соответствующее однородное уравнение записывается в виде \[y» + \left( x \right)y’ + \left( x \right)y = 0.\] Общее решение неоднородного уравнения представляет собой сумму общего решения \(\left( x \right)\) ассоциированного однородного уравнения и частного решения \(Y\left( x \right)\) неоднородного уравнения: \[y\left( x \right) = \left( x \right) + Y\left( x \right).\] Для построения общего решения неоднородного уравнения чаще всего используют следующий подход:

Сначала путем подбора находят частное решение однородного уравнения.

Затем по формуле Лиувилля-Остроградского получают общее решение однородного уравнения.

Далее методом вариации постоянных (методом Лагранжа) определяют общее решение неоднородного уравнения.

Первые два пункта описанной схемы рассмотрены на странице Однородные дифференциальные уравнения второго порядка с переменными коэффициентами . Ниже мы рассмотрим подробнее третий шаг, то есть метод вариации постоянных .

Метод вариации постоянных (или метод Лагранжа) используется для построения общего решения неоднородного уравнения, когда известно общее решение ассоциированного с ним однородного уравнения.

Пусть общее решение однородного уравнения \(2\)-го порядка выражается через фундаментальную систему решений \(\left( x \right)\) и \(\left( x \right):\) \[\left( x \right) = \left( x \right) + \left( x \right),\] где \(,\) − произвольные постоянные. Идея данного метода состоит в том, что вместо постоянных \(\) и \(\) рассматриваются функции \(\left( x \right)\) и \(\left( x \right),\) которые подбираются таким образом, чтобы решение удовлетворяло неоднородному уравнению.

Производные неизвестных функций \(\left( x \right)\) и \(\left( x \right)\) можно определить из системы уравнений \[\left\< \begin \left( x \right)\left( x \right) + \left( x \right)\left( x \right) = 0\\ \left( x \right)\left( x \right) + \left( x \right)\left( x \right) = f\left( x \right) \end \right..\] Главным определителем этой системы является вронскиан функций \(\) и \(,\) который не равен нулю в силу линейной независимости решений \(\) и \(.\) Поэтому данная система уравнений всегда имеет однозначное решение. Окончательные формулы для \(\left( x \right)\) и \(\left( x \right)\) имеют вид \[ <\left( x \right) = — \frac<<\left( x \right)f\left( x \right)>><<,>>\left( x \right)>>,>\;\; <\left( x \right) = \frac<<\left( x \right)f\left( x \right)>><<,>>\left( x \right)>>.> \] Применяя метод вариации параметров, важно помнить, что функция \(f\left( x \right)\) должна соответствовать дифференциальному уравнению, приведенному к стандартному виду, т.е. коэффициент \(\left( x \right)\) перед старшей производной должен быть равен \(1.\)

Далее, зная производные \(\left( x \right)\) и \(\left( x \right),\) можно найти и сами функции \(\left( x \right)\) и \(\left( x \right):\) \[ <\left( x \right) = — \int <\frac<<\left( x \right)f\left( x \right)>><<,>>\left( x \right)>>dx> + ,>\;\; <\left( x \right) = \int <\frac<<\left( x \right)f\left( x \right)>><<,>>\left( x \right)>>dx> + ,> \] где \(,\) \(\) − постоянные интегрирования.

Тогда общее решение исходного неоднородного уравнения будет выражаться формулой \[ \left( x \right)\left( x \right) + \left( x \right)\left( x \right) > = <\left[ < - \int <\frac<<\left( x \right)f\left( x \right)>><<,>>\left( x \right)>>dx> + > \right]\left( x \right) > + <\left[ <\int <\frac<<\left( x \right)f\left( x \right)>><<,>>\left( x \right)>>dx> + > \right]\left( x \right) > = <\left( x \right) + \left( x \right) + Y\left( x \right),> \] в которой \[ = <\left( x \right)\int <\frac<<\left( x \right)f\left( x \right)>><<,>>\left( x \right)>>dx> > — <\left( x \right)\int <\frac<<\left( x \right)f\left( x \right)>><<,>>\left( x \right)>>dx> > \] обозначает частное решение неоднородного уравнения.

Теперь воспользуемся методом вариации постоянных и построим общее решение неоднородного уравнения. Будем рассматривать параметры \(\) и \(\) как функции от переменной \(x.\) Производные этих функций определяются из системы уравнений \[\left\< \begin + x = 0\\ <\left( <> \right)^\prime > + <\left( x \right)^\prime >= 1 + \frac<1><<>> \end \right..\] Здесь правая часть \(1 + \large\frac<1><<>>\normalsize\) во втором уравнении записана после преобразования исходного дифференциального уравнения в стандартную форму: \[ <y» — 2xy’ + 2y = + 1,>\;\; <\Rightarrow y'' - \frac<2>y’ + \frac<2><<>>y = 1 + \frac<1><<>>.> \] Решая данную систему уравнений, находим производные \(\left( x \right),\) \(\left( x \right)\) и затем сами функции \(\left( x \right)\) и \(\left( x \right).\) Имеем \[ <= \frac<1> + \frac<1><<>>,>\;\; <= — 1 — \frac<1><<>>,>\;\; <\Rightarrow = \ln x — \frac<1><<2>> + ,>\;\; <= — x + \frac<1> + ,> \] где \(,\) − постоянные интегрирования.

В результате получаем общее решение неоднородного уравнения в виде \[ \left( x \right) + \left( x \right)x > = <\left( <\ln x - \frac<1><<2>> + > \right) + \left( < - x + \frac<1> + > \right)x > = < + x + \left( <\ln x - 1>\right) + \frac<1><2>.> \]

Теперь, используя метод вариации постоянных, найдем общее решение неоднородного уравнения, которое в стандартном виде записывается как \[y» — \frac<> <\right)>> + \frac<<\left( <\ln x - 1>\right)>> = \frac<<\ln x - 1>>.\] Полагая, что \[y\left( x \right) = \left( x \right)\ln x + \left( x \right)x,\] найдем функции \(\left( x \right)\) и \(\left( x \right)\) из системы уравнений \[ <\left\< \begin \ln x + x = 0\\ <\left( <\ln x>\right)^\prime > + <\left( x \right)^\prime >= \frac<<\ln x - 1>> \end \right.,>\;\; <\Rightarrow \left\< \begin \ln x + x = 0\\ \frac<<>> + = \frac<<\ln x - 1>> \end \right..> \] Умножим второе уравнение на \(x\) и вычтем из него первое уравнение: \[ <\left\< \begin \ln x + x = 0\\ + x = \ln x — 1 \end \right.,>\;\; <\Rightarrow \left( <1 - \ln x>\right) = \ln x — 1,>\;\; <\Rightarrow = — 1.> \] Далее, подставляя \(,\) например, в первое уравнение, находим \(:\) \[ <- \ln x + x = 0,>\;\; <\Rightarrow = \frac<<\ln x>>.> \] Интегрируя, получаем: \[ <= \int <\left( < - 1>\right)dx> = — x + ,>\;\; <= \int <\frac<<\ln x>>dx> > = <\int <\ln x\,d\left( <\ln x>\right)> > = <\frac<<<<\ln >^2>x>> <2>+ ,> \] где \(,\) − постоянные интегрирования.

Итак, общее решение исходного неоднородного уравнения имеет вид: \[ \left( x \right)\ln x + \left( x \right)x > = <\left( < - x + > \right)\ln x + \left( <\frac<<<<\ln >^2>x>> <2>+ > \right)x > = <\ln x + x + \frac<2>\ln x\left( <\ln x - 2>\right).> \]

Источник