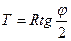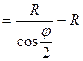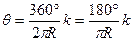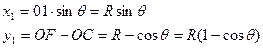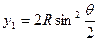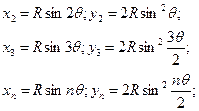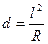ДЕТАЛЬНАЯ РАЗБИВКА КРУГОВЫХ КРИВЫХ
Детальная разбивка кривой предусматривает не только закреп-ление на местности начала НК, конца КК и середины СК кривой, но и обозначение всей кривой, например, колышками через определен-ный интервал. Существует ряд способов разбивки круговых кривых: способ прямоугольных координат, способ углов, способ продолжен-ных хорд.
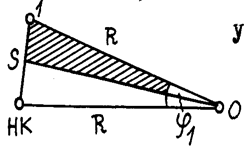
Способ прямоугольных координат (ординат от тангенса).
|
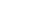
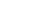


|
|
|
|
|
|
В эти формулы подставляют значение угла j1, зависящее от величины интервала К, которое можно найти из выражения:
j1= 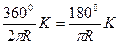
На местности откладывают от начала кривой НК по направ-лению на вершину угла поворота ВУ (по направлению тангенса) абсциссы Хi , а по перпендикулярному направлению ординаты Уi и закрепляют точки 1, 2, 3 и т.д. Так производят разбивку до середины кривой. Другую половину кривой разбивают с ее конца. Для определения координат Х и У существуют специальные таблицы.
Этот способ применяется на ровной площадке и является наиболее точным, так как точки 1, 2, 3 и т.д. выносят независимо друг от друга, поэтому ошибка положения одной точки не окажет влияния на положение других точек, чего нельзя сказать о рассмат-риваемых далее способах углов и продолженных хорд .
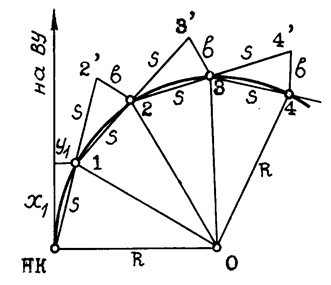
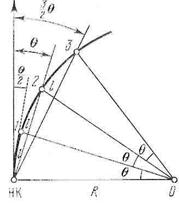
Способ углов (полярный способ).
|
|
|
|
|
Этот способ удобно применять в стесненных условиях, когда есть видимость между НК и точками 1, 2, 3. (например, на высокой насыпи, где способ прямоугольных координат неприемлем).
|
|

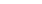
|
|
|
|
Способ продолженных хорд
|
Вначале по координатам Х1 и У1 выносят точку 1. Затем в створе НК-1 на расстоянии S от точки 1 отмечают вспомогательную точку 2’, от которой откладывают так называемое промежуточное
|
|
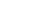




|
|
Этим способом одну половину кривой разбивают с HK, а дру-гую половину — с конца кривой КК. Способ применим в любыхстес-ненных условиях, в том числе и в выемке, где первые два способа неприемлемы.
Недостатком способов углов и продолженных хорд является снижение точности разбивки кривой по мере возрастания ее длины, так как положение каждой последующей точки определяется относительно предыдущей.
Источник
Способы детальной разбивки закруглений



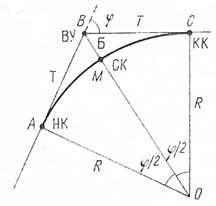
Схема круговой кривой
Для расчета закругления на местности теодолита измеряют угол β, для того чтобы вычислить угол поворота трассы φ=180º–β (φ–угол между первоначальным и последующим направлением трассы)
Радиус закругления R выбирают в соответствии с условиями техники безопасности эксплуатации сооружения и рельефа. По φ и R вычисляют основные элементы круговой кривой.
Тангенс (Т) – расстояние от вершины угла (ВУ) до начало кривой (НК) или конца кривой (КК):
Кривая (К) – длина дуги окружности с радиусом R от НК до КК:
Биссектриса (Б) – расстояние от ВУ до середины кривой (СК):
Б
Домер (Д) – разность путей по ломаной линии и дуге:
За концом кривой все пикеты смещаются вперед на Д.
Для того чтобы разбить круговую кривую на местности достаточно закрепить ее основные точки: начало, середину и конец.
Для того чтобы закрепить НК и КК от ВУ по оси трассы откладывают Т. Для того чтобы закрепить СК, при помощи теодолита откладывают угол β/2 и в этом направлении откладывают Б.
Пикетажное значение НК и КК вычисляют по формулам:
Контроль: КК=ВУ+Т–Д
При больших R не достаточно только закрепить НК, СК, КК. В этом случае пользуются детальной разбивкой круговой кривой, которая выполняется, например, способом прямоугольных координат, продолженных хорд и т.д.
Дальше приступают к нивелированию трассы, которое начинают с привязки трассы к реперу ГВС. Привязка заключается в проложении нивелирного хода о репера до начала трассы (ПК0). Далее нивелируют пикеты, «плюсовые» точки, поперечники, главные точки кривых. Нивелирование выполняется геометрическим способом «из середины», причем пикеты нивелируют как связующие точки (по двум сторонам реек), а остальные как промежуточные (по черной стороне). Заканчивается нивелирование привязкой трассы к реперу высотной сети.
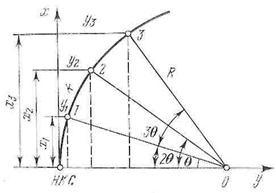
Способ прямоугольных координат является наиболее точным и простым; он применяется в открытой равнинной местности. В этом способе положение точек на кривой через равные промежутки k определяется прямоугольными координатами х и y; за ось абсцисс принимают линию тангенса (касательной), а за начало координат — начало (НК) или конец кривой (КК).
Для вычисления координат х, у точек детальной разбивки предварительно вычисляют центральный угол θ, соответствующий заданной дуге k,
Далее, решая прямоугольный треугольник ОС1, получают:
или
Аналогичным образом вычисляют координаты последующих точек, расположенных на первой половине кривой, через расстояние k по дуге кривой:
Определение положения точек 1, 2, 3, кривой на местности сводится к откладыванию рулеткой от НК (или КК) по направлению тангенса отрезков х1, х2, х3 построению при помощи эккера (теодолита) перпендикуляров из концов этих отрезков и откладыванию по ним отрезков у1, у2, у3
Разбивку ведут от начала кривой (НК) до середины, а затем от конца кривой (КК) также до середины кривой (СК). Обе половины кривой должны сомкнуться в точке СК, что контролирует точность детальной разбивки. Достоинством данного способа является то, что положение каждой точки кривой определяется независимыми промерами и при переходе от одной точки к другой погрешности не накапливаются.
Полярный способ (способ углов) целесообразно применять на косогорах, насыпях и в полузакрытой равнинной местности. Способ базируется на положении геометрии о том, что угол с вершиной в какой-либо точке кривой, образованный касательной и секущей, равен половине соответствующего центрального угла. Как видно из рисунка, хорда 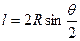
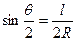
Положение точек кривой на местности определяют линейно-угловыми засечками. Для этого теодолит устанавливают в точке НК (или КК) и от направления тангенса откладывают последовательно углы 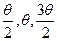
Недостатком способа является снижение точности детальной разбивки с увеличением числа точек, так как положение каждой последующей точки находится относительно предыдущей.

Способ продолженных хорд применяют при разбивке кривых на застроенных и залесенных участках, в выемках и тоннелях.
Разбивку кривой ведут с помощью мерной ленты и рулетки. По радиусу кривой R и принятой длине хорды l вычисляют длину отрезка d, называемого промежуточным перемещением.
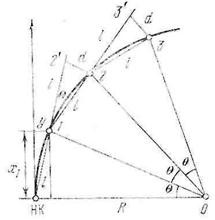
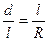
Положение первой точки кривой находят способом прямоугольных координат; при этом значения координат х1 и у1 вычисляют по формулам (1) и (2). Закрепив на местности точку 1, на продолжении створа линии НК-1 откладывают длину хорды l и отмечают временную точку 2′. Затем находят положение точки 2 на кривой линейной засечкой отрезками I из точки 1 и d из точки 2». Положение остальных точек детальной разбивки до середины кривой находится аналогичным образом.
Данный способ имеет тот же недостаток, что и полярный способ.
Источник

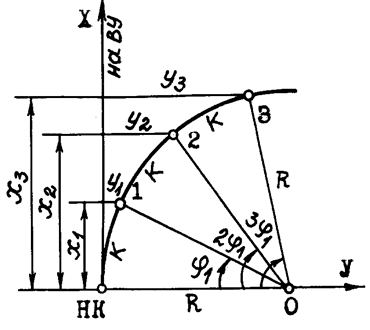
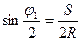 (из решения заштрихованного треугольника), причем в этом способе S явля-ется хордой определенной длины.
(из решения заштрихованного треугольника), причем в этом способе S явля-ется хордой определенной длины.