Дерево решений как способ выбора альтернативы

Дерево решений: пример. Алгоритмы построения дерева принятия решений

Метод дерева решений — это прекрасный способ выбрать стратегию последовательных действий в условиях риска. Именно риск здесь выступает ключевым словом, поскольку при опасности принять рациональное решение очень сложно, а продуманный план помогает проанализировать сложившуюся ситуацию.

Дерево принятия решений подобно настоящему: у него есть ствол, ветви и листья. «Ствол» — основа всего — это главный вопрос , на который нужно ответить. Ветви — это стрелочки с несколькими вариантами ответов. А листья — это ситуации , к которым приведет нас выбранный ответ.

Самый простой пример

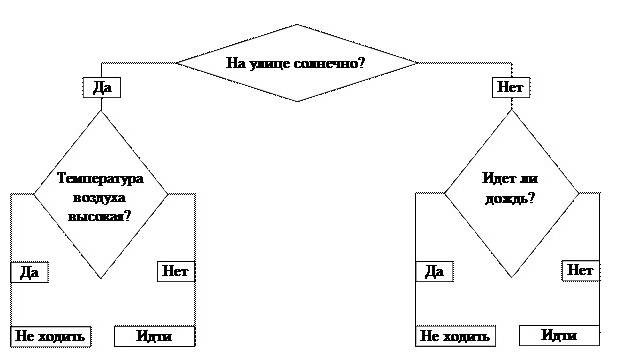
Любая теория воспринимается намного легче, если привести пример. Дерево решений «Пойти гулять? » — это самый простой алгоритм. В бизнесе все базируется на таких принципах . Кстати, в основе всех электронных программ тоже лежит алгоритм построения дерева.

Итак, стоит задача: решить, можно ли идти гулять. Наш ствол — первый вопрос — это ключевой фактор: «На улице солнечно?» От него зависит наш дальнейший путь. Если ответ положительный, двигаемся по направлению слова «Да». Приходим к новому разветвлению . Если температура воздуха высокая, мы получаем окончательный ответ — «Не и дти гулять», в противном случае тоже получаем итог, но уже с результатом «И дти гулять».

Можно было выбрать и другой путь. Дерево принятия решений подразумевает, что будут проанализированы все варианты движения и спрогнозированы результаты .

Почему следует выбирать этот метод

Преимущества дерева решений позволяют определить, почему данный метод является самым гибким из всех, что касаются вопроса о выборе решений.

• Это одномерная схема, которая наглядно показывает п ричинно -следственные связи. Ч то будет, если. И куда наш выбор приведет.
• Возможность одновременно рассматривать нетипичные ситуации и подбирать несколько вариантов их разрешения.
• Отсутствие каких-либо законов следствия.
• Простота в использовании.
• Работать над моделью может сразу несколько человек, что облегчает задачу.
• Дерево решений не ограничено во временных рамках.
• Подходит для большинства бизнес-ситуаций.

Область применения

Можно привести любой пример дерева решений. Это может быть вопрос о том, открывать ли новые производственные мощности, внедрять технологии, формировать новый ассортимент и т. д. Область применения данного метода невероятно широка.

Но можно выделить три большие группы, где дерево решений помогает выиграть время.

• Описание данных. Допустим, задача руководства — решить пробле му расширения ассортимента. Схема данной задачи будет состоять из конкретных цифр возможных сумм прибыли и рентабельности. С труктурировать такую информацию будет намного проще, если она будет храниться в виде схемы, а не в обширной таблице.
• Классификация. Появляется возможность сгруппировать исходные данные и сделать для них подборку.
• Регрессия. Дерево решений позволяет определить, как формируется целевая стратегия под воздействием независимых факторов. Например, на выбор стратегии формирования ассортимента будут влиять, кроме основных факторов производства, второстепенные, которые косвенно к этому относятся . Это может быть урожай какао-бобов из страны-экспортера или график движения транспортных судов. Вроде бы на выбор стратегии прямо не оказывают воздействия, но сбой их работы может помешать формированию ассортимента на кондитерской фабрике.

Алгоритмы

На сегодняшний день существует несколько известных алгоритмов, позволяющих создавать дерева решений (примеры мы уже рассмотрели).

• CART — аббревиатура слов Classification and Regression Tree (классификация и регрессия). Согласно его принципам, каждый узел дерева может иметь только два отв етвления .
• С4.5 — метод построения, при котором каждый узел может иметь неограниче нное количество веток. В такой схеме тяжело делать прогнозы, поэтому ее используют для классификации.
• QUEST ( Quick , U nbiased , E fficient S tatistical Trees ). Самая сложная из всех моделей, но очень достоверная. П озволяет создавать многомерное ветвление . Это значит, что в любом узле м ожет создаваться не просто множество веток, а примеров действия.

Сбор данных

Метод дерева решений будет эффективен в том случае, если правильно подойти к вопросу сбора данных. Приведем характерную последовательность:

• Определение жизненного цикла проекта: сколько будет этапов и какова продолжительность каждого из них.
• Выделение ключевых событий, на этапе которых может возникнуть дилемма выбрать одно или другое.
• Описание каждого из возможных факторов, которые повлияют на наступление того или иного события, описанного в предыдущем шаге.
• О ценка вероятности принятия этих решений.
• Расчет стоимости всех этапов жизненного цикла (считается между ключевыми событиями).

Пример дерева решений

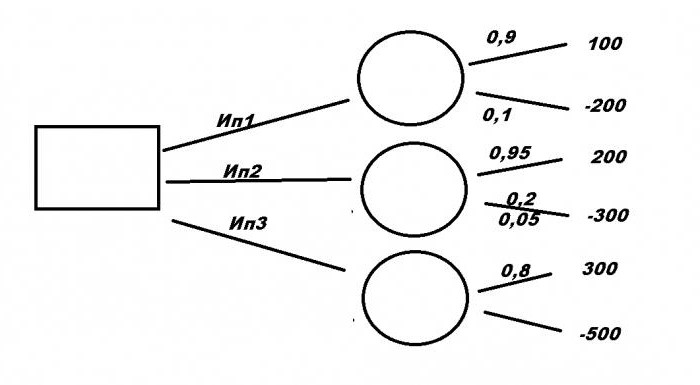
Рассмотрим типичную бизнес -ситуацию. Компании нужно выбрать выгодное инвестиционное вложение Ип1, Ип2, Ип3 с помощью дерева решений. Примеры решения задач формируются на основании исходных данных.

Первый проект требует вложения в размере 200 млн р ублей и принесет прибыль 100 млн руб . Для второго необходимо 300 млн р уб. , но принесет 200 млн руб . Третий, самый прибыльный, — 3 00 млн руб ., но вложить нужно 500. При этом есть риск потерять все. При первом варианте уровень риска — 10 %, при втором — 5 %, и при третьем — 20 %. Какой из проектов будет самый выгодный?

Провести математические расчеты довольно затруднительно. Поэтому нужно построить графическую схему. Правильное решение будет зависеть не только от того, насколько понятной будет модель, но и как будут расположены исходные данные.

Построение графика

Итак, у нас есть три проекта: Ип1, Ип2 и Ип3. Рассмотрим, как составить дерево решений. Двигаться будем от первого ключевого момента, обозначенного большим квадратом. Здесь мы напишем конечный итог, а пока пускай сектор остается пустым. От него чертим три ответвления с именами проектов. Далее каждый вариант имеет свой уровень математических ожиданий, обозначенный кружочком. Пока они пустые, в них нужно будет написать полученный результат расчетов. От каждого из них будет еще два ответвления. Вверх — это доход и уровень его ожидания, вниз — затраты и риски потерь.

Математические расчеты

Пора приступать к поиску правильного решения. Для этого составим формулы:

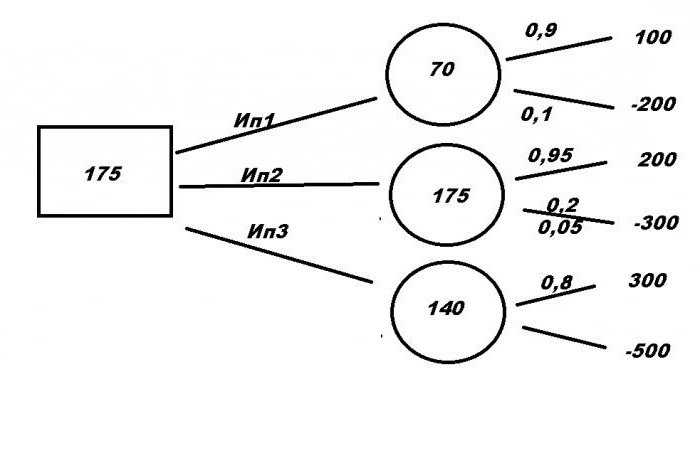
• Ип1= 100 × 0.9 — 200 × 0.1 = 70
• Ип2 = 200 × 0.95 — 300 × 0.05 = 175
• Ип3 = 300 × 0.8 — 500 × 0.2 = 140

Полученные данные записываем в кружочки. Выбираем наибольшее число — 175. И записываем его в квадрат. Это и есть математическое ожидание от проекта. И поскольку самое выгодное предложение — это Ип2, это и будет являться ответом на задачу.

Область применения

Казалось бы, что примеров дерева решений для бизнеса можно привести неограниче нное количество . Действительно, чаще всего об этом методе говорят в контексте менеджмента. Н о на самом деле область применения алгоритма намного больше. П риведем некоторые интересные факты:

• Дерево решений незаменимо в банковском деле. Его используют для оценки клиентов и принятия решения для выдачи кредита.
• Промышленность. Яркий пример — проверка качества. Поскольку на заводах не всегда есть возможность оценить все выпускаемые товары практическим методом, создают специальный алгоритм, с помощью которого брак отсекается на нескольких этапах проверки.
• Медицина. Для использования дерева решений в этой сфере не нужны листик и бумага. Л юбой врач делает это ежедневно при постановке диагноза. Доктор задает пациенту наводящие вопросы, о тветы на которые приведут к единому правильному решению.
• Молекулярная биология. Даже в этой уникальной области есть где применить метод построения схем. Например, анализ строения аминокислот.
• Программирование. Любая программа или веб-страница построены по принципу алгоритма и движения от целого к множеству.

Пример использования алгоритма в банковской сфере

Попробуем построить дерево решений, представив, что мы сотрудники отдела кредитования любого банка. Обозначим ключевых факторы:

• возраст;
• уровень дохода;
• иждивенцы , семейное положение;
• кредиты в других организациях;
• наличие движимого и недвижимого имущества.

Теперь по каждой из ключевых веток необходимо составить примерный план возможных действий.

Начнем с возраста. Больше 21? Ответ «да» или «нет». «Нет» сразу приводит нас к нулю. После ответа «Д а» двигаемся к следующему вопросу.

Уровень дохода выше 50 000 руб. в месяц? «Нет» — это сразу ноль , «Да» — переходим к следующей ветке.

Семейное положение . В этом разделе могут появляться дополнительные отв етвления , которые будут важными для нашего решения. Сколько человек в семье? Скол ько из них иждивенцы , какой доход у супруги\супруга. Если ответы нас удовлетворили, можно переходить к следующему сектору.

Кредиты в других организациях. Здесь рационально выделить: какую сумму брали, как быстро отдали, есть ли долги?

Наличие движимого и недвижимого имущества может стать дополнительной гарантией возврата средств, поэтому, если потенциальный заемщик дошел до этого этапа и положительно ответил на последний вопрос, то однозначно решение о выдаче ему денег будет позитивным.

Сократить путь к любому из решений «Выдать» или «Не выдать» можно на любом этапе .

Пример из медицины

Рассмотрим типичную ситуацию. К врачу пришел на осмотр пациент с кашлем. При постановке диагноза доктор оценивает человека по нескольким параметрам:

• как давно кашель;
• есть ли температура;
• заложен ли нос;
• как прослушиваются легкие, бронхи, наличие хрипов;
• сердечный ритм;
• возраст, наличие флюрографии и др. факторы.

Ответ на каждый из этих вопросов приведет доктора к постановке правильного диагноза.

Вывод

Пример дерева решений можно встретить в повседневной жизни. Люди сотни раз сталкиваются с дилеммой , решить которую можно, выбрав только самый короткий или самый выгодный путь. То чно так же и в бизнесе. Алгоритм помогает выбрать правильное решение, классифицировать и структурировать данные о вопросе, спрогнозировать исход. Важной задачей является выбор основных вопросов, которые составляют ключевые моменты, и ветвей с результатом. Существует множество моделей, компьютерных программ, позволяющих быстро и качественно построить дерево решений и облегчить поиск.

Источник

Деревья решений: общие принципы

Деревья решений — один из методов автоматического анализа данных. Разбираем общие принципы работы и области применения.

Деревья решений являются одним из наиболее эффективных инструментов интеллектуального анализа данных и предсказательной аналитики, которые позволяют решать задачи классификации и регрессии.

Они представляют собой иерархические древовидные структуры, состоящие из решающих правил вида «Если . то . ». Правила автоматически генерируются в процессе обучения на обучающем множестве и, поскольку они формулируются практически на естественном языке (например, «Если объём продаж более 1000 шт., то товар перспективный»), деревья решений как аналитические модели более вербализуемы и интерпретируемы, чем, скажем, нейронные сети.

Поскольку правила в деревьях решений получаются путём обобщения множества отдельных наблюдений (обучающих примеров), описывающих предметную область, то по аналогии с соответствующим методом логического вывода их называют индуктивными правилами, а сам процесс обучения — индукцией деревьев решений.

В обучающем множестве для примеров должно быть задано целевое значение, т.к. деревья решений являются моделями, строящимися на основе обучения с учителем. При этом, если целевая переменная дискретная (метка класса), то модель называют деревом классификации, а если непрерывная, то деревом регрессии.

Основополагающие идеи, послужившие толчком к появлению и развитию деревьев решений, были заложены в 1950-х годах в области исследований моделирования человеческого поведения с помощью компьютерных систем. Среди них следует выделить работы К. Ховеленда «Компьютерное моделирование мышления»[1] и Е. Ханта и др. «Эксперименты по индукции»[2].

Дальнейшее развитие деревьев решений как самообучающихся моделей для анализа данных связано с именами Джона Р. Куинлена[3], который разработал алгоритм ID3 и его усовершенствованные модификации С4.5 и С5.0, а так же Лео Бреймана[4], который предложил алгоритм CART и метод случайного леса.

Терминология

Введем в рассмотрение основные понятия, используемые в теории деревьев решений.

Название	Описание
Объект	Пример, шаблон, наблюдение
Атрибут	Признак, независимая переменная, свойство
Целевая переменная	Зависимая переменная, метка класса
Узел	Внутренний узел дерева, узел проверки
Корневой узел	Начальный узел дерева решений
Лист	Конечный узел дерева, узел решения, терминальный узел
Решающее правило	Условие в узле, проверка

Структура дерева решений

Собственно, само дерево решений — это метод представления решающих правил в иерархической структуре, состоящей из элементов двух типов — узлов (node) и листьев (leaf). В узлах находятся решающие правила и производится проверка соответствия примеров этому правилу по какому-либо атрибуту обучающего множества.

В простейшем случае, в результате проверки, множество примеров, попавших в узел, разбивается на два подмножества, в одно из которых попадают примеры, удовлетворяющие правилу, а в другое — не удовлетворяющие.

Затем к каждому подмножеству вновь применяется правило и процедура рекурсивно повторяется пока не будет достигнуто некоторое условие остановки алгоритма. В результате в последнем узле проверка и разбиение не производится и он объявляется листом. Лист определяет решение для каждого попавшего в него примера. Для дерева классификации — это класс, ассоциируемый с узлом, а для дерева регрессии — соответствующий листу модальный интервал целевой переменной.

Таким образом, в отличие от узла, в листе содержится не правило, а подмножество объектов, удовлетворяющих всем правилам ветви, которая заканчивается данным листом.

Очевидно, чтобы попасть в лист, пример должен удовлетворять всем правилам, лежащим на пути к этому листу. Поскольку путь в дереве к каждому листу единственный, то и каждый пример может попасть только в один лист, что обеспечивает единственность решения.

Задачи

Основная сфера применения деревьев решений — поддержка процессов принятия управленческих решений, используемая в статистике, анализе данных и машинном обучении. Задачами, решаемыми с помощью данного аппарата, являются:

• Классификация — отнесение объектов к одному из заранее известных классов. Целевая переменная должна иметь дискретные значения.
• Регрессия (численное предсказание) — предсказание числового значения независимой переменной для заданного входного вектора.
• Описание объектов — набор правил в дереве решений позволяет компактно описывать объекты. Поэтому вместо сложных структур, описывающих объекты, можно хранить деревья решений.

Процесс построения

Процесс построения деревьев решений заключается в последовательном, рекурсивном разбиении обучающего множества на подмножества с применением решающих правил в узлах. Процесс разбиения продолжается до тех пор, пока все узлы в конце всех ветвей не будут объявлены листьями. Объявление узла листом может произойти естественным образом (когда он будет содержать единственный объект, или объекты только одного класса), или по достижении некоторого условия остановки, задаваемого пользователем (например, минимально допустимое число примеров в узле или максимальная глубина дерева).

Алгоритмы построения деревьев решений относят к категории так называемых жадных алгоритмов. Жадными называются алгоритмы, которые допускают, что локально-оптимальные решения на каждом шаге (разбиения в узлах), приводят к оптимальному итоговому решению. В случае деревьев решений это означает, что если один раз был выбран атрибут, и по нему было произведено разбиение на подмножества, то алгоритм не может вернуться назад и выбрать другой атрибут, который дал бы лучшее итоговое разбиение. Поэтому на этапе построения нельзя сказать обеспечит ли выбранный атрибут, в конечном итоге, оптимальное разбиение.

В основе большинства популярных алгоритмов обучения деревьев решений лежит принцип «разделяй и властвуй». Алгоритмически этот принцип реализуется следующим образом. Пусть задано обучающее множество S , содержащее n примеров, для каждого из которых задана метка класса C_i(i=1..k) , и m атрибутов A_j(j=1..m) , которые, как предполагается, определяют принадлежность объекта к тому или иному классу. Тогда возможны три случая:

1. Все примеры множества S имеют одинаковую метку класса C_i (т.е. все обучающие примеры относятся только к одному классу). Очевидно, что обучение в этом случае не имеет смысла, поскольку все примеры, предъявляемые модели, будут одного класса, который и «научится» распознавать модель. Само дерево решений в этом случае будет представлять собой лист, ассоциированный с классом C_i . Практическое использование такого дерева бессмысленно, поскольку любой новый объект оно будет относить только к этому классу.
2. Множество S вообще не содержит примеров, т.е. является пустым множеством. В этом случае для него тоже будет создан лист (применять правило, чтобы создать узел, к пустому множеству бессмысленно), класс которого будет выбран из другого множества (например, класс, который наиболее часто встречается в родительском множестве).
3. Множество S содержит обучающие примеры всех классов C_k . В этом случае требуется разбить множество S на подмножества, ассоциированные с классами. Для этого выбирается один из атрибутов A_j множества S который содержит два и более уникальных значения (a_1,a_2. a_p) , где p — число уникальных значений признака. Затем множество S разбивается на p подмножеств (S_1,S_2. S_p) , каждое из которых включает примеры, содержащие соответствующее значение атрибута. Затем выбирается следующий атрибут и разбиение повторяется. Это процедура будет рекурсивно повторяться до тех пор, пока все примеры в результирующих подмножествах не окажутся одного класса.

Описанная выше процедура лежит в основе многих современных алгоритмов построения деревьев решений. Очевидно, что при использовании данной методики, построение дерева решений будет происходить сверху вниз (от корневого узла к листьям).

В настоящее время разработано значительное число алгоритмов обучения деревья решений: ID3, CART, C4.5, C5.0, NewId, ITrule, CHAID, CN2 и т.д. Но наибольшее распространение и популярность получили следующие:

• ID3 (Iterative Dichotomizer 3) — алгоритм позволяет работать только с дискретной целевой переменной, поэтому деревья решений, построенные с помощью данного алгоритма, являются классифицирующими. Число потомков в узле дерева не ограничено. Не может работать с пропущенными данными.
• C4.5 — усовершенствованная версия алгоритма ID3, в которую добавлена возможность работы с пропущенными значениями атрибутов (по версии издания Springer Science в 2008 году алгоритм занял 1-е место в топ-10 наиболее популярных алгоритмов Data Mining).
• CART (Classification and Regression Tree) — алгоритм обучения деревьев решений, позволяющий использовать как дискретную, так и непрерывную целевую переменную, то есть решать как задачи классификации, так и регрессии. Алгоритм строит деревья, которые в каждом узле имеют только два потомка.

Основные этапы построения

В ходе построения дерева решений нужно решить несколько основных проблем, с каждой из которых связан соответствующий шаг процесса обучения:

1. Выбор атрибута, по которому будет производиться разбиение в данном узле (атрибута разбиения).
2. Выбор критерия остановки обучения.
3. Выбор метода отсечения ветвей (упрощения).
4. Оценка точности построенного дерева.

Рассмотрим эти этапы ниже.

Выбор атрибута разбиения

При формировании правила для разбиения в очередном узле дерева необходимо выбрать атрибут, по которому это будет сделано. Общее правило для этого можно сформулировать следующим образом: выбранный атрибут должен разбить множество наблюдений в узле так, чтобы результирующие подмножества содержали примеры с одинаковыми метками класса, или были максимально приближены к этому, т.е. количество объектов из других классов («примесей») в каждом из этих множеств было как можно меньше. Для этого были выбраны различные критерии, наиболее популярными из которых стали теоретико-информационный и статистический.

Теоретико-информационный критерий

Как следует из названия, критерий основан на понятиях теории информации, а именно — информационной энтропии.

где n — число классов в исходном подмножестве, N_i — число примеров i-го класса, N — общее число примеров в подмножестве.

Таким образом, энтропия может рассматриваться как мера неоднородности подмножества по представленным в нём классам. Когда классы представлены в равных долях и неопределённость классификации наибольшая, энтропия также максимальна. Если все примеры в узле относятся к одному классу, т.е. N=N_i , логарифм от единицы обращает энтропию в ноль.

Таким образом, лучшим атрибутом разбиения A_j будет тот, который обеспечит максимальное снижение энтропии результирующего подмножества относительно родительского. На практике, однако, говорят не об энтропии, а о величине, обратной ей, которая называется информацией. Тогда лучшим атрибутом разбиения будет тот, который обеспечит максимальный прирост информации результирующего узла относительно исходного:

где \text(S) — информация, связанная с подмножеством S до разбиения, \text(S_A) — информация, связанная с подмножеством, полученными при разбиении по атрибуту A .

Таким образом, задача выбора атрибута разбиения в узле заключается в максимизации величины \text(A) , называемой приростом информации (от англ. gain — прирост, увеличение). Поэтому сам теоретико-информационный подход известен как критерий прироста информации. Он впервые был применён в алгоритме ID3, а затем в C4.5 и других алгоритмах.

Статистический подход

В основе статистического подхода лежит использование индекса Джини (назван в честь итальянского статистика и экономиста Коррадо Джини). Статистический смысл данного показателя в том, что он показывает — насколько часто случайно выбранный пример обучающего множества будет распознан неправильно, при условии, что целевые значения в этом множестве были взяты из определённого статистического распределения.

Таким образом индекс Джини фактически показывает расстояние между двумя распределениями — распределением целевых значений, и распределением предсказаний модели. Очевидно, что чем меньше данное расстояние, тем лучше работает модель.

Индекс Джини может быть рассчитан по формуле:

где Q — результирующее множество, n — число классов в нём, p_i — вероятность i-го класса (выраженная как относительная частота примеров соответствующего класса). Очевидно, что данный показатель меняется от 0 до 1. При этом он равен 0, если все примеры Q относятся к одному классу, и равен 1, когда классы представлены в равных пропорциях и равновероятны. Тогда лучшим будет то разбиение, для которого значение индекса Джини будут минимальным.

Критерий остановки алгоритма

Теоретически, алгоритм обучения дерева решений будет работать до тех пор, пока в результате не будут получены абсолютно «чистые» подмножества, в каждом из которых будут примеры одного класса. Правда, возможно при этом будет построено дерево, в котором для каждого примера будет создан отдельный лист. Очевидно, что такое дерево окажется бесполезным, поскольку оно будет переобученным — каждому примеру будет соответствовать свой уникальный путь в дереве, а следовательно, и набор правил, актуальный только для данного примера.

Переобучение в случае дерева решений ведёт к тем же последствиям, что и для нейронной сети — точное распознавание примеров, участвующих в обучении и полная несостоятельность на новых данных. Кроме этого, переобученные деревья имеют очень сложную структуру, и поэтому их сложно интерпретировать.

Очевидным решением проблемы является принудительная остановка построения дерева, пока оно не стало переобученным. Для этого разработаны следующие подходы.

1. Ранняя остановка — алгоритм будет остановлен, как только будет достигнуто заданное значение некоторого критерия, например процентной доли правильно распознанных примеров. Единственным преимуществом подхода является снижение времени обучения. Главным недостатком является то, что ранняя остановка всегда делается в ущерб точности дерева, поэтому многие авторы рекомендуют отдавать предпочтение отсечению ветвей.
2. Ограничение глубины дерева — задание максимального числа разбиений в ветвях, по достижении которого обучение останавливается. Данный метод также ведёт к снижению точности дерева.
3. Задание минимально допустимого число примеров в узле — запретить алгоритму создавать узлы с числом примеров меньше заданного (например, 5). Это позволит избежать создания тривиальных разбиений и, соответственно, малозначимых правил.

Все перечисленные подходы являются эвристическими, т.е. не гарантируют лучшего результата или вообще работают только в каких-то частных случаях. Поэтому к их использованию следует подходить с осторожностью. Каких-либо обоснованных рекомендаций по тому, какой метод лучше работает, в настоящее время тоже не существует. Поэтому аналитикам приходится использовать метод проб и ошибок.

Отсечение ветвей

Как было отмечено выше, если «рост» дерева не ограничить, то в результате будет построено сложное дерево с большим числом узлов и листьев. Как следствие оно будет трудно интерпретируемым. В то же время решающие правила в таких деревьях, создающие узлы, в которые попадают два-три примера, оказываются малозначимыми с практической точки зрения.

Гораздо предпочтительнее иметь дерево, состоящее из малого количества узлов, которым бы соответствовало большое число примеров из обучающей выборки. Поэтому представляет интерес подход, альтернативный ранней остановке — построить все возможные деревья и выбрать то из них, которое при разумной глубине обеспечивает приемлемый уровень ошибки распознавания, т.е. найти наиболее выгодный баланс между сложностью и точностью дерева.

К сожалению, это задача относится к классу NP-полных задач, что было показано Л. Хайфилем (L. Hyafill) и Р. Ривестом (R. Rivest), и, как известно, этот класс задач не имеет эффективных методов решения.

Альтернативным подходом является так называемое отсечение ветвей (pruning). Он содержит следующие шаги:

1. Построить полное дерево (чтобы все листья содержали примеры одного класса).
2. Определить два показателя: относительную точность модели — отношение числа правильно распознанных примеров к общему числу примеров, и абсолютную ошибку — число неправильно классифицированных примеров.
3. Удалить из дерева листья и узлы, отсечение которых не приведёт к значимому уменьшению точности модели или увеличению ошибки.

Отсечение ветвей, очевидно, производится в направлении, противоположном направлению роста дерева, т.е. снизу вверх, путём последовательного преобразования узлов в листья. Преимуществом отсечения ветвей по сравнению с ранней остановкой является возможность поиска оптимального соотношения между точностью и понятностью дерева. Недостатком является большее время обучения из-за необходимости сначала построить полное дерево.

Извлечение правил

Иногда даже упрощённое дерево решений все ещё является слишком сложным для визуального восприятия и интерпретации. В этом случае может оказаться полезным извлечь из дерева решающие правила и организовать их в наборы, описывающие классы.

Для извлечения правил нужно отследить все пути от корневого узла к листьям дерева. Каждый такой путь даст правило, состоящее из множества условий, представляющих собой проверку в каждом узле пути.

Визуализация сложных деревьев решений в виде решающих правил вместо иерархической структуры из узлов и листьев может оказаться более удобной для визуального восприятия.

Преимущества алгоритма

Рассмотрев основные проблемы, возникающие при построении деревьев, было бы несправедливо не упомянуть об их достоинствах:

• быстрый процесс обучения;
• генерация правил в областях, где эксперту трудно формализовать свои знания;
• извлечение правил на естественном языке;
• интуитивно понятная классификационная модель;
• высокая точность предсказания, сопоставимая с другими методами анализа данных (статистика, нейронные сети);
• построение непараметрических моделей.

В силу этих и многих других причин, деревья решений являются важным инструментом в работе каждого специалиста, занимающегося анализом данных.

Области применения

Модули для построения и исследования деревьев решений входят в состав большинства аналитических платформ. Они являются удобным инструментом в системах поддержки принятия решений и интеллектуального анализа данных.

Деревья решений успешно применяются на практике в следующих областях:

• Банковское дело. Оценка кредитоспособности клиентов банка при выдаче кредитов.
• Промышленность. Контроль за качеством продукции (выявление дефектов), испытания без разрушений (например, проверка качества сварки) и т.д.
• Медицина. Диагностика заболеваний.
• Молекулярная биология. Анализ строения аминокислот.
• Торговля. Классификация клиентов и товаров.

Это далеко не полный список областей где можно использовать деревья решений. Вместе с анализом данных деревья решений постоянно расширяют круг своего использования, становясь важным инструментом управления бизнес-процессами и поддержки принятия решений.

Источник