Дерево решений как способ принятия решений

Дерево решений: пример. Алгоритмы построения дерева принятия решений

Метод дерева решений — это прекрасный способ выбрать стратегию последовательных действий в условиях риска. Именно риск здесь выступает ключевым словом, поскольку при опасности принять рациональное решение очень сложно, а продуманный план помогает проанализировать сложившуюся ситуацию.

Дерево принятия решений подобно настоящему: у него есть ствол, ветви и листья. «Ствол» — основа всего — это главный вопрос , на который нужно ответить. Ветви — это стрелочки с несколькими вариантами ответов. А листья — это ситуации , к которым приведет нас выбранный ответ.

Самый простой пример

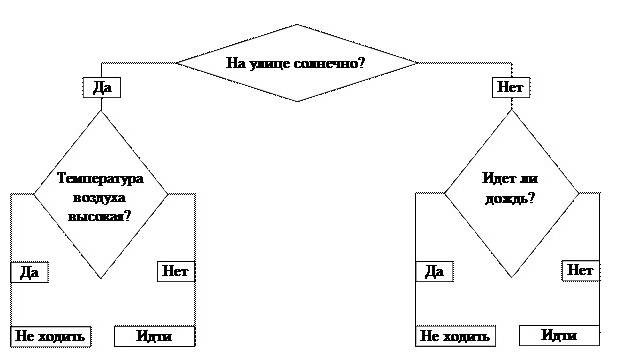
Любая теория воспринимается намного легче, если привести пример. Дерево решений «Пойти гулять? » — это самый простой алгоритм. В бизнесе все базируется на таких принципах . Кстати, в основе всех электронных программ тоже лежит алгоритм построения дерева.

Итак, стоит задача: решить, можно ли идти гулять. Наш ствол — первый вопрос — это ключевой фактор: «На улице солнечно?» От него зависит наш дальнейший путь. Если ответ положительный, двигаемся по направлению слова «Да». Приходим к новому разветвлению . Если температура воздуха высокая, мы получаем окончательный ответ — «Не и дти гулять», в противном случае тоже получаем итог, но уже с результатом «И дти гулять».

Можно было выбрать и другой путь. Дерево принятия решений подразумевает, что будут проанализированы все варианты движения и спрогнозированы результаты .

Почему следует выбирать этот метод

Преимущества дерева решений позволяют определить, почему данный метод является самым гибким из всех, что касаются вопроса о выборе решений.

• Это одномерная схема, которая наглядно показывает п ричинно -следственные связи. Ч то будет, если. И куда наш выбор приведет.
• Возможность одновременно рассматривать нетипичные ситуации и подбирать несколько вариантов их разрешения.
• Отсутствие каких-либо законов следствия.
• Простота в использовании.
• Работать над моделью может сразу несколько человек, что облегчает задачу.
• Дерево решений не ограничено во временных рамках.
• Подходит для большинства бизнес-ситуаций.

Область применения

Можно привести любой пример дерева решений. Это может быть вопрос о том, открывать ли новые производственные мощности, внедрять технологии, формировать новый ассортимент и т. д. Область применения данного метода невероятно широка.

Но можно выделить три большие группы, где дерево решений помогает выиграть время.

• Описание данных. Допустим, задача руководства — решить пробле му расширения ассортимента. Схема данной задачи будет состоять из конкретных цифр возможных сумм прибыли и рентабельности. С труктурировать такую информацию будет намного проще, если она будет храниться в виде схемы, а не в обширной таблице.
• Классификация. Появляется возможность сгруппировать исходные данные и сделать для них подборку.
• Регрессия. Дерево решений позволяет определить, как формируется целевая стратегия под воздействием независимых факторов. Например, на выбор стратегии формирования ассортимента будут влиять, кроме основных факторов производства, второстепенные, которые косвенно к этому относятся . Это может быть урожай какао-бобов из страны-экспортера или график движения транспортных судов. Вроде бы на выбор стратегии прямо не оказывают воздействия, но сбой их работы может помешать формированию ассортимента на кондитерской фабрике.

Алгоритмы

На сегодняшний день существует несколько известных алгоритмов, позволяющих создавать дерева решений (примеры мы уже рассмотрели).

• CART — аббревиатура слов Classification and Regression Tree (классификация и регрессия). Согласно его принципам, каждый узел дерева может иметь только два отв етвления .
• С4.5 — метод построения, при котором каждый узел может иметь неограниче нное количество веток. В такой схеме тяжело делать прогнозы, поэтому ее используют для классификации.
• QUEST ( Quick , U nbiased , E fficient S tatistical Trees ). Самая сложная из всех моделей, но очень достоверная. П озволяет создавать многомерное ветвление . Это значит, что в любом узле м ожет создаваться не просто множество веток, а примеров действия.

Сбор данных

Метод дерева решений будет эффективен в том случае, если правильно подойти к вопросу сбора данных. Приведем характерную последовательность:

• Определение жизненного цикла проекта: сколько будет этапов и какова продолжительность каждого из них.
• Выделение ключевых событий, на этапе которых может возникнуть дилемма выбрать одно или другое.
• Описание каждого из возможных факторов, которые повлияют на наступление того или иного события, описанного в предыдущем шаге.
• О ценка вероятности принятия этих решений.
• Расчет стоимости всех этапов жизненного цикла (считается между ключевыми событиями).

Пример дерева решений

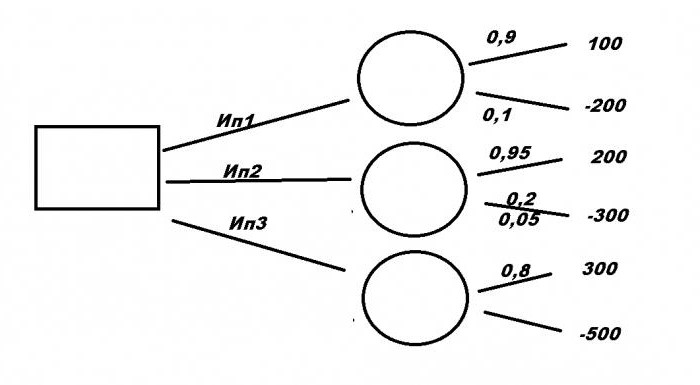
Рассмотрим типичную бизнес -ситуацию. Компании нужно выбрать выгодное инвестиционное вложение Ип1, Ип2, Ип3 с помощью дерева решений. Примеры решения задач формируются на основании исходных данных.

Первый проект требует вложения в размере 200 млн р ублей и принесет прибыль 100 млн руб . Для второго необходимо 300 млн р уб. , но принесет 200 млн руб . Третий, самый прибыльный, — 3 00 млн руб ., но вложить нужно 500. При этом есть риск потерять все. При первом варианте уровень риска — 10 %, при втором — 5 %, и при третьем — 20 %. Какой из проектов будет самый выгодный?

Провести математические расчеты довольно затруднительно. Поэтому нужно построить графическую схему. Правильное решение будет зависеть не только от того, насколько понятной будет модель, но и как будут расположены исходные данные.

Построение графика

Итак, у нас есть три проекта: Ип1, Ип2 и Ип3. Рассмотрим, как составить дерево решений. Двигаться будем от первого ключевого момента, обозначенного большим квадратом. Здесь мы напишем конечный итог, а пока пускай сектор остается пустым. От него чертим три ответвления с именами проектов. Далее каждый вариант имеет свой уровень математических ожиданий, обозначенный кружочком. Пока они пустые, в них нужно будет написать полученный результат расчетов. От каждого из них будет еще два ответвления. Вверх — это доход и уровень его ожидания, вниз — затраты и риски потерь.

Математические расчеты

Пора приступать к поиску правильного решения. Для этого составим формулы:

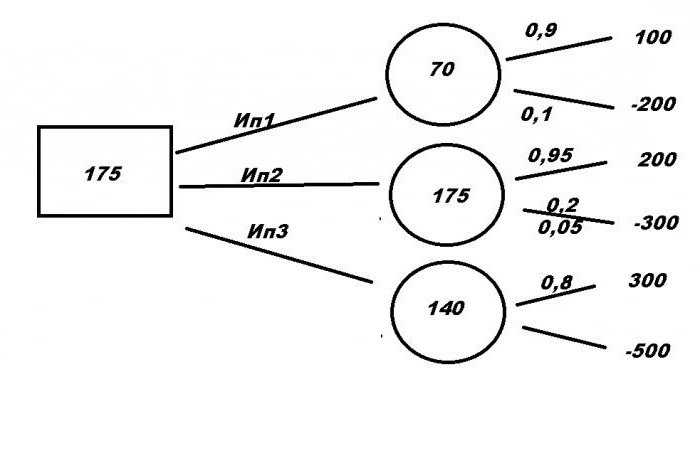
• Ип1= 100 × 0.9 — 200 × 0.1 = 70
• Ип2 = 200 × 0.95 — 300 × 0.05 = 175
• Ип3 = 300 × 0.8 — 500 × 0.2 = 140

Полученные данные записываем в кружочки. Выбираем наибольшее число — 175. И записываем его в квадрат. Это и есть математическое ожидание от проекта. И поскольку самое выгодное предложение — это Ип2, это и будет являться ответом на задачу.

Область применения

Казалось бы, что примеров дерева решений для бизнеса можно привести неограниче нное количество . Действительно, чаще всего об этом методе говорят в контексте менеджмента. Н о на самом деле область применения алгоритма намного больше. П риведем некоторые интересные факты:

• Дерево решений незаменимо в банковском деле. Его используют для оценки клиентов и принятия решения для выдачи кредита.
• Промышленность. Яркий пример — проверка качества. Поскольку на заводах не всегда есть возможность оценить все выпускаемые товары практическим методом, создают специальный алгоритм, с помощью которого брак отсекается на нескольких этапах проверки.
• Медицина. Для использования дерева решений в этой сфере не нужны листик и бумага. Л юбой врач делает это ежедневно при постановке диагноза. Доктор задает пациенту наводящие вопросы, о тветы на которые приведут к единому правильному решению.
• Молекулярная биология. Даже в этой уникальной области есть где применить метод построения схем. Например, анализ строения аминокислот.
• Программирование. Любая программа или веб-страница построены по принципу алгоритма и движения от целого к множеству.

Пример использования алгоритма в банковской сфере

Попробуем построить дерево решений, представив, что мы сотрудники отдела кредитования любого банка. Обозначим ключевых факторы:

• возраст;
• уровень дохода;
• иждивенцы , семейное положение;
• кредиты в других организациях;
• наличие движимого и недвижимого имущества.

Теперь по каждой из ключевых веток необходимо составить примерный план возможных действий.

Начнем с возраста. Больше 21? Ответ «да» или «нет». «Нет» сразу приводит нас к нулю. После ответа «Д а» двигаемся к следующему вопросу.

Уровень дохода выше 50 000 руб. в месяц? «Нет» — это сразу ноль , «Да» — переходим к следующей ветке.

Семейное положение . В этом разделе могут появляться дополнительные отв етвления , которые будут важными для нашего решения. Сколько человек в семье? Скол ько из них иждивенцы , какой доход у супруги\супруга. Если ответы нас удовлетворили, можно переходить к следующему сектору.

Кредиты в других организациях. Здесь рационально выделить: какую сумму брали, как быстро отдали, есть ли долги?

Наличие движимого и недвижимого имущества может стать дополнительной гарантией возврата средств, поэтому, если потенциальный заемщик дошел до этого этапа и положительно ответил на последний вопрос, то однозначно решение о выдаче ему денег будет позитивным.

Сократить путь к любому из решений «Выдать» или «Не выдать» можно на любом этапе .

Пример из медицины

Рассмотрим типичную ситуацию. К врачу пришел на осмотр пациент с кашлем. При постановке диагноза доктор оценивает человека по нескольким параметрам:

• как давно кашель;
• есть ли температура;
• заложен ли нос;
• как прослушиваются легкие, бронхи, наличие хрипов;
• сердечный ритм;
• возраст, наличие флюрографии и др. факторы.

Ответ на каждый из этих вопросов приведет доктора к постановке правильного диагноза.

Вывод

Пример дерева решений можно встретить в повседневной жизни. Люди сотни раз сталкиваются с дилеммой , решить которую можно, выбрав только самый короткий или самый выгодный путь. То чно так же и в бизнесе. Алгоритм помогает выбрать правильное решение, классифицировать и структурировать данные о вопросе, спрогнозировать исход. Важной задачей является выбор основных вопросов, которые составляют ключевые моменты, и ветвей с результатом. Существует множество моделей, компьютерных программ, позволяющих быстро и качественно построить дерево решений и облегчить поиск.

Источник

1.10. Деревья решений ¶

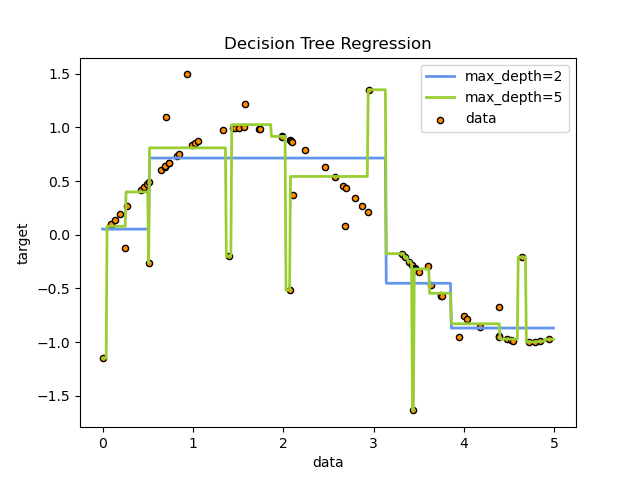
Деревья решений (DT) — это непараметрический контролируемый метод обучения, используемый для классификации и регрессии . Цель состоит в том, чтобы создать модель, которая предсказывает значение целевой переменной, изучая простые правила принятия решений, выведенные из характеристик данных. Дерево можно рассматривать как кусочно-постоянное приближение.

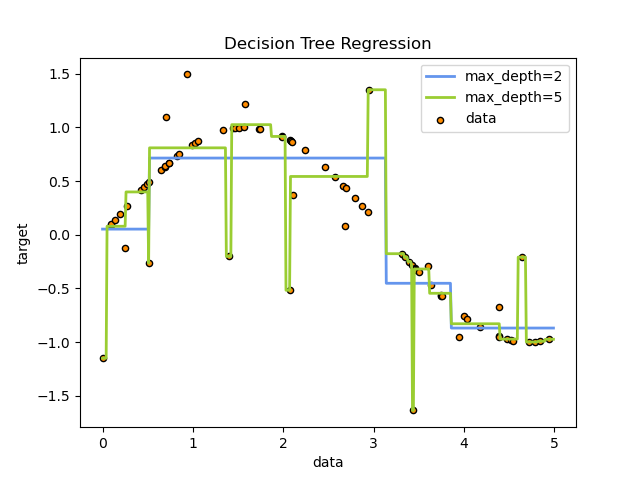
Например, в приведенном ниже примере деревья решений обучаются на основе данных, чтобы аппроксимировать синусоидальную кривую с набором правил принятия решений «если-то-еще». Чем глубже дерево, тем сложнее правила принятия решений и тем лучше модель.

Некоторые преимущества деревьев решений:

• Просто понять и интерпретировать. Деревья можно визуализировать.
• Требуется небольшая подготовка данных. Другие методы часто требуют нормализации данных, создания фиктивных переменных и удаления пустых значений. Однако обратите внимание, что этот модуль не поддерживает отсутствующие значения.
• Стоимость использования дерева (т. Е. Прогнозирования данных) является логарифмической по количеству точек данных, используемых для обучения дерева.
• Может обрабатывать как числовые, так и категориальные данные. Однако реализация scikit-learn пока не поддерживает категориальные переменные. Другие методы обычно специализируются на анализе наборов данных, содержащих только один тип переменных. См. Алгоритмы для получения дополнительной информации.
• Способен обрабатывать проблемы с несколькими выходами.
• Использует модель белого ящика. Если данная ситуация наблюдаема в модели, объяснение условия легко объяснить с помощью булевой логики. Напротив, в модели черного ящика (например, в искусственной нейронной сети) результаты могут быть труднее интерпретировать.
• Возможна проверка модели с помощью статистических тестов. Это позволяет учитывать надежность модели.
• Работает хорошо, даже если его предположения несколько нарушаются истинной моделью, на основе которой были сгенерированы данные.

К недостаткам деревьев решений можно отнести:

• Обучающиеся дереву решений могут создавать слишком сложные деревья, которые плохо обобщают данные. Это называется переобучением. Чтобы избежать этой проблемы, необходимы такие механизмы, как обрезка, установка минимального количества выборок, необходимых для конечного узла, или установка максимальной глубины дерева.
• Деревья решений могут быть нестабильными, поскольку небольшие изменения в данных могут привести к созданию совершенно другого дерева. Эта проблема смягчается за счет использования деревьев решений в ансамбле.
• Как видно из рисунка выше, предсказания деревьев решений не являются ни гладкими, ни непрерывными, а являются кусочно-постоянными приближениями. Следовательно, они не годятся для экстраполяции.
• Известно, что проблема обучения оптимальному дереву решений является NP-полной с точки зрения нескольких аспектов оптимальности и даже для простых концепций. Следовательно, практические алгоритмы обучения дереву решений основаны на эвристических алгоритмах, таких как жадный алгоритм, в котором локально оптимальные решения принимаются в каждом узле. Такие алгоритмы не могут гарантировать возврат глобального оптимального дерева решений. Это можно смягчить путем обучения нескольких деревьев в учащемся ансамбля, где функции и образцы выбираются случайным образом с заменой.
• Существуют концепции, которые трудно изучить, поскольку деревья решений не выражают их легко, например проблемы XOR, четности или мультиплексора.
• Ученики дерева решений создают предвзятые деревья, если некоторые классы доминируют. Поэтому рекомендуется сбалансировать набор данных перед подгонкой к дереву решений.

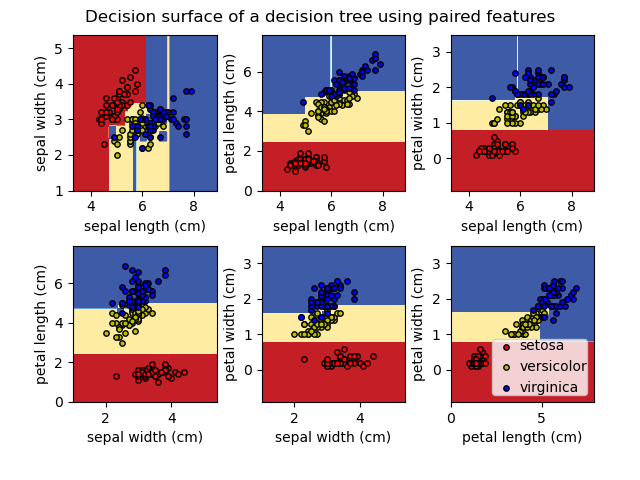
1.10.1. Классификация

DecisionTreeClassifier — это класс, способный выполнять мультиклассовую классификацию набора данных.

Как и в случае с другими классификаторами, DecisionTreeClassifier принимает в качестве входных данных два массива: массив X, разреженный или плотный, формы (n_samples, n_features), содержащий обучающие образцы, и массив Y целочисленных значений, формы (n_samples,), содержащий метки классов для обучающих образцов:

После подбора модель можно использовать для прогнозирования класса образцов:

В случае, если существует несколько классов с одинаковой и самой высокой вероятностью, классификатор предскажет класс с самым низким индексом среди этих классов.

В качестве альтернативы выводу определенного класса можно предсказать вероятность каждого класса, которая представляет собой долю обучающих выборок класса в листе:

DecisionTreeClassifier поддерживает как двоичную (где метки — [-1, 1]), так и мультиклассовую (где метки — [0,…, K-1]) классификацию.

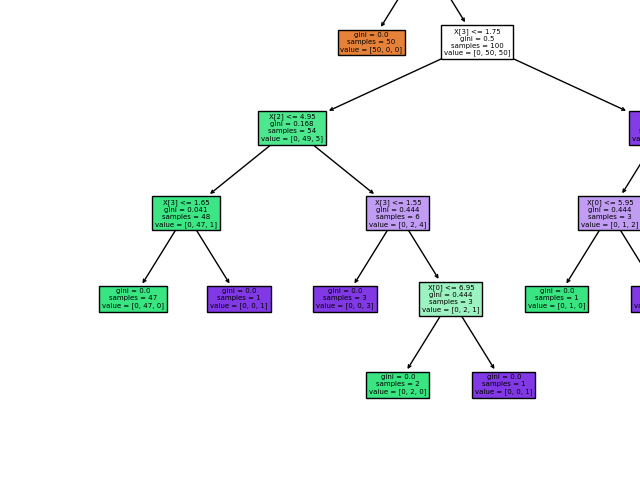
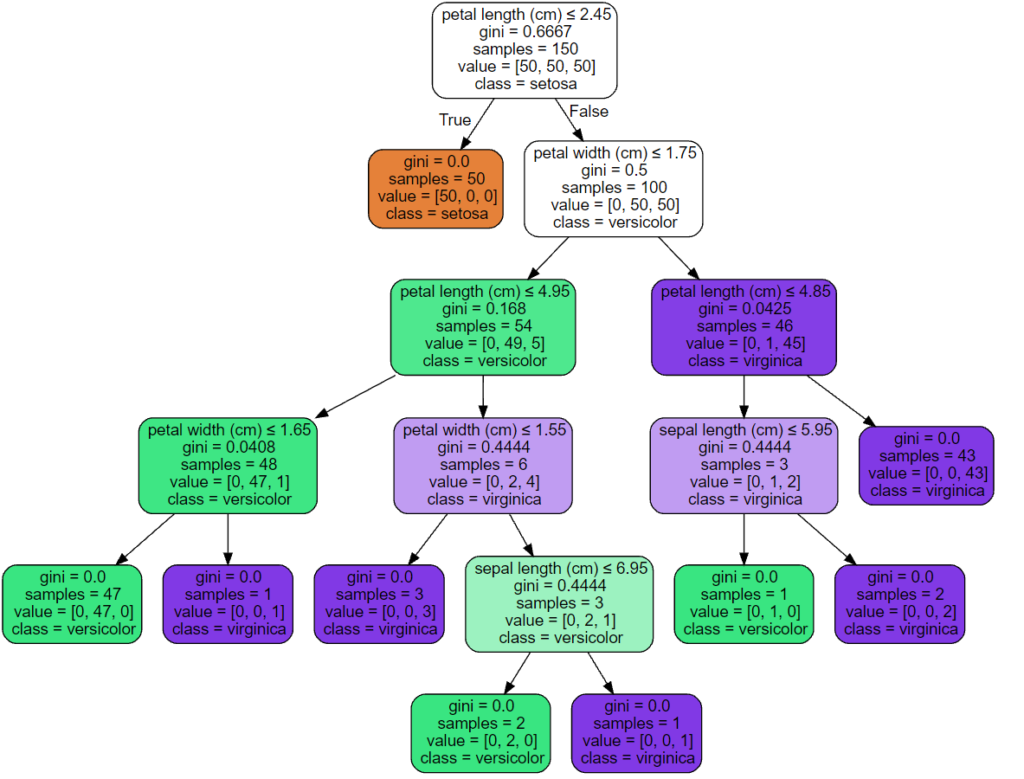
Используя набор данных Iris, мы можем построить дерево следующим образом:

После обучения вы можете построить дерево с помощью plot_tree функции:

Мы также можем экспортировать дерево в формат Graphviz с помощью export_graphviz экспортера. Если вы используете Conda менеджер пакетов, то Graphviz бинарные файлы и пакет питон может быть установлен conda install python-graphviz .

В качестве альтернативы двоичные файлы для graphviz можно загрузить с домашней страницы проекта graphviz, а оболочку Python установить из pypi с помощью pip install graphviz .

Ниже приведен пример экспорта graphviz вышеуказанного дерева, обученного на всем наборе данных радужной оболочки глаза; результаты сохраняются в выходном файле iris.pdf :

Экспортер export_graphviz также поддерживает множество эстетических вариантов, в том числе окраски узлов их класс (или значение регрессии) и используя явные имена переменных и классов , если это необходимо. Блокноты Jupyter также автоматически отображают эти графики встроенными:

В качестве альтернативы дерево можно также экспортировать в текстовый формат с помощью функции export_text . Этот метод не требует установки внешних библиотек и более компактен:

1.10.2. Регрессия

Деревья решений также могут применяться к задачам регрессии с помощью класса DecisionTreeRegressor .

Как и в настройке классификации, метод fit будет принимать в качестве аргументов массивы X и y, только в этом случае ожидается, что y будет иметь значения с плавающей запятой вместо целочисленных значений:

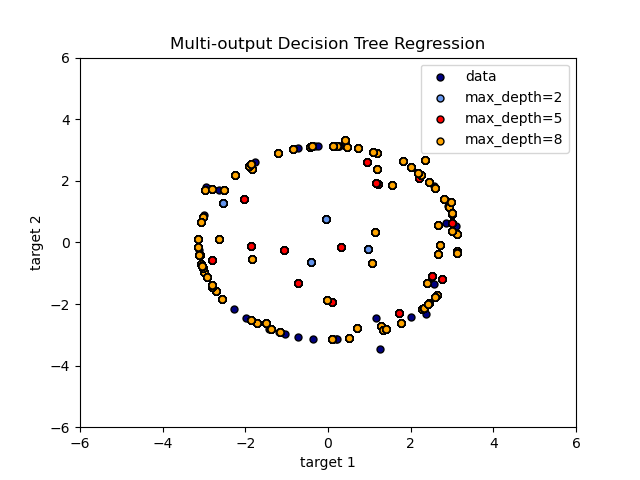
1.10.3. Проблемы с несколькими выходами

Задача с несколькими выходами — это проблема контролируемого обучения с несколькими выходами для прогнозирования, то есть когда Y — это 2-й массив формы (n_samples, n_outputs) .

Когда нет корреляции между выходами, очень простой способ решить эту проблему — построить n независимых моделей, то есть по одной для каждого выхода, а затем использовать эти модели для независимого прогнозирования каждого из n выходов. Однако, поскольку вполне вероятно, что выходные значения, относящиеся к одному и тому же входу, сами коррелированы, часто лучшим способом является построение единой модели, способной прогнозировать одновременно все n выходов. Во-первых, это требует меньшего времени на обучение, поскольку строится только один оценщик. Во-вторых, часто можно повысить точность обобщения итоговой оценки.

Что касается деревьев решений, эту стратегию можно легко использовать для поддержки задач с несколькими выходами. Для этого требуются следующие изменения:

• Сохранять n выходных значений в листьях вместо 1;
• Используйте критерии разделения, которые вычисляют среднее сокращение для всех n выходов.

Этот модуль предлагает поддержку для задач с несколькими выходами, реализуя эту стратегию как в, так DecisionTreeClassifier и в DecisionTreeRegressor . Если дерево решений соответствует выходному массиву Y формы (n_samples, n_outputs), то итоговая оценка будет:

• Вывести значения n_output при predict ;
• Выведите список массивов n_output вероятностей классов на predict_proba .

Использование деревьев с несколькими выходами для регрессии продемонстрировано в разделе «Регрессия дерева решений с несколькими выходами» . В этом примере вход X — это одно действительное значение, а выходы Y — синус и косинус X.

Использование деревьев с несколькими выходами для классификации демонстрируется в разделе «Завершение лица с оценками с несколькими выходами» . В этом примере входы X — это пиксели верхней половины граней, а выходы Y — пиксели нижней половины этих граней.

1.10.4. Сложность

В общем, время выполнения для построения сбалансированного двоичного дерева составляет $O(n_n_\log(n_))$ и время запроса $O(\log(n_))$. Хотя алгоритм построения дерева пытается генерировать сбалансированные деревья, они не всегда будут сбалансированными. Предполагая, что поддеревья остаются примерно сбалансированными, стоимость на каждом узле состоит из перебора $O(n_)$ найти функцию, обеспечивающую наибольшее снижение энтропии. Это стоит $O(n_n_\log(n_))$ на каждом узле, что приводит к общей стоимости по всем деревьям (суммируя стоимость на каждом узле) $O(n_n_^<2>\log(n_))$

1.10.5. Советы по практическому использованию

• Деревья решений имеют тенденцию чрезмерно соответствовать данным с большим количеством функций. Получение правильного соотношения образцов к количеству функций важно, поскольку дерево с небольшим количеством образцов в многомерном пространстве, скорее всего, переоборудуется.
• Предварительно рассмотрите возможность уменьшения размерности (PCA, ICA, или Feature selection), чтобы дать вашему дереву больше шансов найти отличительные признаки.
• Понимание структуры дерева решений поможет лучше понять, как дерево решений делает прогнозы, что важно для понимания важных функций данных.
• Визуализируйте свое дерево во время тренировки с помощью export функции. Используйте max_depth=3 в качестве начальной глубины дерева, чтобы понять, насколько дерево соответствует вашим данным, а затем увеличьте глубину.
• Помните, что количество образцов, необходимых для заполнения дерева, удваивается для каждого дополнительного уровня, до которого дерево растет. Используйте max_depth для управления размером дерева во избежание переобучения.
• Используйте min_samples_split или, min_samples_leaf чтобы гарантировать, что несколько выборок информируют каждое решение в дереве, контролируя, какие разделения будут учитываться. Очень маленькое число обычно означает, что дерево переоборудуется, тогда как большое число не позволяет дереву изучать данные. Попробуйте min_samples_leaf=5 в качестве начального значения. Если размер выборки сильно различается, в этих двух параметрах можно использовать число с плавающей запятой в процентах. В то время как min_samples_split может создавать произвольно маленькие листья, min_samples_leaf гарантирует, что каждый лист имеет минимальный размер, избегая малодисперсных, чрезмерно подходящих листовых узлов в задачах регрессии. Для классификации с несколькими классами min_samples_leaf=1 это часто лучший выбор.

Обратите внимание, что min_samples_split выборки рассматриваются напрямую и независимо от них sample_weight , если они предусмотрены (например, узел с m взвешенными выборками по-прежнему обрабатывается как имеющий ровно m выборок). Рассмотрим min_weight_fraction_leaf или min_impurity_decrease если учет образцов весов требуются при расколах.

Перед обучением сбалансируйте набор данных, чтобы дерево не смещалось в сторону доминирующих классов. Балансировка классов может быть выполнена путем выборки равного количества выборок из каждого класса или, предпочтительно, путем нормализации суммы весов выборок ( sample_weight ) для каждого класса к одному и тому же значению. Также обратите внимание, что критерии предварительного отсечения на основе веса, такие как min_weight_fraction_leaf , будут менее смещены в сторону доминирующих классов, чем критерии, которые не знают весов выборки, например min_samples_leaf .

Если выборки взвешены, будет проще оптимизировать древовидную структуру, используя основанный на весе критерий предварительной отсечения, например min_weight_fraction_leaf , который гарантирует, что конечные узлы содержат по крайней мере часть общей суммы весов выборки.

Все деревья решений np.float32 внутренне используют массивы. Если данные обучения не в этом формате, будет сделана копия набора данных.

Если входная матрица X очень разреженная, рекомендуется преобразовать ее в разреженную csc_matrix перед вызовом соответствия и разреженную csr_matrix перед вызовом предсказания. Время обучения может быть на порядки меньше для входной разреженной матрицы по сравнению с плотной матрицей, когда функции имеют нулевые значения в большинстве выборок.

1.10.6. Алгоритмы дерева: ID3, C4.5, C5.0 и CART

Что представляют собой различные алгоритмы дерева решений и чем они отличаются друг от друга? Какой из них реализован в scikit-learn?

ID3 (Iterative Dichotomiser 3) был разработан Россом Куинланом в 1986 году. Алгоритм создает многостороннее дерево, находя для каждого узла (т. Е. Жадным образом) категориальный признак, который даст наибольший информационный выигрыш для категориальных целей. Деревья вырастают до максимального размера, а затем обычно применяется этап обрезки, чтобы улучшить способность дерева обобщать невидимые данные.

C4.5 является преемником ID3 и снял ограничение, что функции должны быть категориальными, путем динамического определения дискретного атрибута (на основе числовых переменных), который разбивает непрерывное значение атрибута на дискретный набор интервалов. C4.5 преобразует обученные деревья (т. Е. Результат алгоритма ID3) в наборы правил «если-то». Затем оценивается точность каждого правила, чтобы определить порядок, в котором они должны применяться. Удаление выполняется путем удаления предусловия правила, если без него точность правила улучшается.

C5.0 — это последняя версия Quinlan под частной лицензией. Он использует меньше памяти и создает меньшие наборы правил, чем C4.5, но при этом является более точным.

CART (Classification and Regression Trees — деревья классификации и регрессии) очень похож на C4.5, но отличается тем, что поддерживает числовые целевые переменные (регрессию) и не вычисляет наборы правил. CART строит двоичные деревья, используя функцию и порог, которые дают наибольший прирост информации в каждом узле.

scikit-learn использует оптимизированную версию алгоритма CART; однако реализация scikit-learn пока не поддерживает категориальные переменные.

1.10.7. Математическая постановка

Данные обучающие векторы $x_i \in R^n$, i = 1,…, l и вектор-метка $y \in R^l$ дерево решений рекурсивно разбивает пространство признаков таким образом, что образцы с одинаковыми метками или аналогичными целевыми значениями группируются вместе.

Пусть данные в узле m быть представлен $Q_m$ с участием $N_m$ образцы. Для каждого раскола кандидатов $\theta = (j, t_m)$ состоящий из функции $j$ и порог $t_m$, разделите данные на $Q_m^(\theta)$ а также $Q_m^(\theta)$ подмножества
$$Q_m^(\theta) = <(x, y) | x_j predict_proba для этого региона установлено значение $p_$. Общие меры примеси следующие.

Энтропия:
$$H(Q_m) = — \sum_k p_ \log(p_)$$

Неверная классификация:
$$H(Q_m) = 1 — \max(p_)$$

1.10.7.2. Критерии регрессии

Если целью является непрерывное значение, то для узла m, общими критериями, которые необходимо минимизировать для определения местоположений будущих разделений, являются среднеквадратичная ошибка (ошибка MSE или L2), отклонение Пуассона, а также средняя абсолютная ошибка (ошибка MAE или L1). MSE и отклонение Пуассона устанавливают прогнозируемое значение терминальных узлов равным изученному среднему значению $\bar_m$ узла, тогда как MAE устанавливает прогнозируемое значение терминальных узлов равным медиане $median(y)_m$.

Половинное отклонение Пуассона:
$$H(Q_m) = \frac<1> \sum_ (y \log\frac<\bar_m> — y + \bar_m)$$

Настройка criterion=»poisson» может быть хорошим выбором, если ваша цель — счетчик или частота (количество на какую-то единицу). В любом случае, y>=0 является необходимым условием для использования этого критерия. Обратите внимание, что он подходит намного медленнее, чем критерий MSE.

Обратите внимание, что он подходит намного медленнее, чем критерий MSE.

1.10.8. Обрезка с минимальными затратами и сложностью

Сокращение с минимальными затратами и сложностью — это алгоритм, используемый для сокращения дерева во избежание чрезмерной подгонки, описанный в главе 3 [BRE] . Этот алгоритм параметризован $\alpha\ge0$ известный как параметр сложности. Параметр сложности используется для определения меры затрат и сложности, $R_\alpha(T)$ данного дерева $T$:
$$R_\alpha(T) = R(T) + \alpha|\widetilde|$$

где $|\widetilde|$ количество конечных узлов в $T$ а также $R(T)$ традиционно определяется как общий коэффициент ошибочной классификации конечных узлов. В качестве альтернативы scikit-learn использует взвешенную общую примесь конечных узлов для $R(T)$. Как показано выше, примесь узла зависит от критерия. Обрезка с минимальными затратами и сложностью находит поддеревоT что сводит к минимуму $R_\alpha(T)$.

Оценка сложности стоимости одного узла составляет $R_\alpha(t)=R(t)+\alpha$. Ответвление $T_t$, определяется как дерево, в котором узел $t$ это его корень. В общем, примесь узла больше, чем сумма примесей его конечных узлов, $R(T_t) ccp_alpha параметра.

Источник