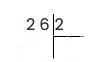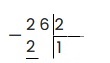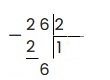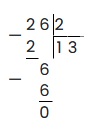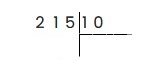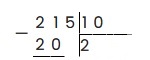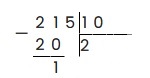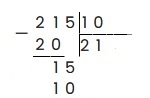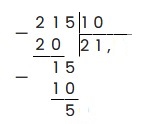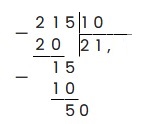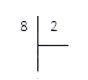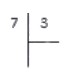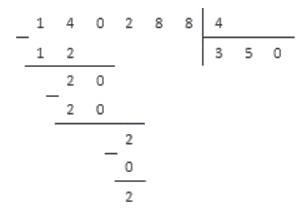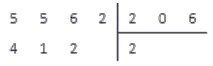Деление столбиком способом подбора

Деление в столбик

Сегодня мы рассмотрим вопрос, касающийся деления в столбик. Познакомимся с алгоритмом и закрепим материал на конкретных примерах.

Алгоритм деления в столбик

Делить столбиком гораздо проще, чем считать в уме. Для этого необходимо воспользоваться простым алгоритмом:

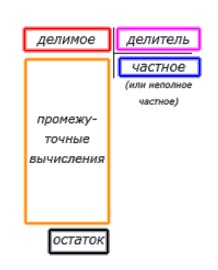
1. Слева размещаем делимое, справа делитель, рисуем уголок
2. В делимом выделяем наименьшее число, которое можно разделить на делитель;
3. Производим деление, в частное записываем результат деления (целое число), в промежуточные вычисления — остаток (делитель умножаем на текущую цифру из частного);
4. Делитель умножаем на полученную цифру в частном, считаем разность двух цифр, которая будет остатком.
5. Скидываем одну цифру из делимого в остаток;
6. В случае, если остаток меньше делителя, а в делимом еще остались цифры, скидываем цифру с делимого в остаток, а в частном ставим запятую;
7. В случае, если остаток меньше делителя, а требуемая точность вычисления не достигнута, при этом в делимом больше не осталось цифр, то добавляем по нулю в остаток и в частное (если в частном еще не было запятой — то вместо нуля ставим запятую);
8. Повторяем пункты 3-6 до тех пор пока, в делимом не останется цифр, а остаток не будет равен нулю (или не будет достигнута требуемая точность вычислений)

Примеры

Рассмотрим несколько примеров на закрепление алгоритма деления в столбик.

Пример 1: Разделить 26 на 2.

Слева записываем делимое, справа делитель, рисуем уголок.

Делимое у нас — 26, делитель — 2. Наименьшее число, которое можно взять из делимого и разделить на 2, будет двойка. 2 делим на 2, получаем 1. 2 умножить на 1 получится 2. Записываем это:

2 — 2 = 0, ноль писать не обязательно, поэтому исходя из алгоритма скидываем следующую цифру из делимого — 6

6 делим на 2 получаем 3, записываем в частное. 3 умножаем на 2 получаем 6. 6 — 6 = 0

Ответ: 26 : 2 = 13

Пример 2: Разделить 215 на 10.

Аналогично предыдущему примеру записываем условие уголком:

Наименьшее число, которое можно выделить из 215 и разделить на 10 — это 21. 21 делим на 10, и записываем в частное целую часть — 2. 2 умножаем на 10 — получаем 20:

21 — 20 = 1, записываем в остаток:

Сбрасываем из делимого оставшуюся цифру — 5, получаем 15. Аналогично делим 15 на 10 и получаем целую часть 1. 1 умножаем на 10, получаем 10, записываем:

15 — 10 = 5, записываем в остаток. 5 нацело на 10 не делится. Возвращаемся к 7 пункту алгоритма и ставим запятую в частном:

А, к остатку добавляем 0:

Теперь 50 мы легко можем разделить на 10 без остатка:

Источник

Как быстро научить ребенка делить столбиком?

Чтобы упростить деление чисел, традиционно используется метод деления в столбик. Не все дети понимают принцип с первого раза, а многие взрослые уже успели его забыть. Давайте разберемся, как без лишних слов объяснить ребенку деление «уголком», чтобы он научился решать примеры с двузначными, трехзначными и даже четырехзначными числами.

Как правильно делить в столбик?

Удобнее рассмотреть сам процесс на несложной иллюстрации (№1).

Как найти частное двух чисел – 35 и 5?

1. Пишем числа, участвующие в делении, так:
   
   Делимое в данном случае – 35, делитель – 5. Под делителем пишется частное.
2. Находим неполное частное. Посмотрим на первую цифру слева. В нашем случае это 3, и оно меньше 5 – значит, добавляем следующую цифру слева и будем работать с этой величиной (у нас 35).
3. Определяем, какое количество пятерок (5) поместится в 35. Вспоминаем таблицу умножения и заключаем, что в 35 поместиться 7 пятерок. Значит, в графе частное записываем 7.
   
4. Проверяем правильность действий путем умножения: 7 X 5=35. Все верно, решение выполнено точно.

Что нужно знать ребенку для понимания деления столбиком?

Чтобы любимое чадо освоило, как делить уголком (в столбик), нужно два условия:

• отличное знание таблицы умножения;
• умение быстро считать в уме.

В конце 3 класса ученики усваивают, как разделить простые двузначные числа.

При переходе в 4 класс дети учатся делить многозначные числа (больше, чем 100). Также происходит обучение делению уголком чисел с двузначным и трехзначным делителем, решение примеров с остатком.

Методика обучения детей делению столбиком

Если школьник пропустил занятия по математике либо не смог усвоить знания на уроке, то родители должны сами донести до него нужную информацию. Спешка в таком деле неуместна – быстро не значит хорошо. Следует проявить терпение. Деление чисел – простое дело для взрослого, а для школьника задача весьма сложная.

Проверьте знание таблицы умножения. Если ребенок не умножает «автоматически», позвольте подсматривать в табличку.

Первый пример можно взять простейший, с делением без остатка на однозначное число (как в иллюстрации №1).

Когда малыш понял принцип и успешно справился с несложным заданием, пора научить его делению трехзначных чисел. Выполним пример №2.

Работа с многозначными числами

Задание 2: разделим 372 на 6. Для этого на листке бумаги производим следующие действия:

1. Определяем делимое (372) и делитель (6), оформляем запись в уголок:
   
2. Неполное частное в нашем варианте, конечно, 37 (т. к. в 3 не поместится 6 ни разу, берем следующую цифру).
3. Считаем, много ли шестерок уместится в 37. Если 36:6, то получим 6. Получившееся 6 пишем в графе «частное», а 36 пишем под делителем.
4. Вычитаем из 37-36=1. Пишем единичку слева внизу под чертой:
   
5. В единичке не поместится ни одной шестерки, значит, берем оставшуюся цифру из делимого (2). Получилось 12. Нужно определить, сколько в 12 поместится 6 (12 больше 6 ровно в два раза). Получаем 2. Записываем в частное получившуюся величину:
   

Пример решен, можно проверить правильность путем умножения: 62X6=372.

Как объяснить деление с остатком?

Иногда разделить на равные доли невозможно. Легче всего объяснить такую ситуацию школьнику на несложной задаче. Например:

В группе 8 учеников, на обед им выдали 18 ватрушек на подносе. Когда каждый получит по 2 ватрушки (18:8=2 и ост. 2), на подносе останутся лишние 2 штуки. Это и есть остаток.

Решение столбиком с остатком, по математическому правилу, записывается точно так же, как и без него. Разница лишь в том, что в конце остаток будет. В этом варианте правильно прописать количество целых единиц и количество единиц в остатке (пример: 4 целых и 9 в остатке).

Обучение школьника должно проходить поэтапно, от простых примеров к более сложным. Если нет понимания простых действий в делении, значит, нужно повторить информацию еще раз. Постепенно решение примеров начнет происходить быстрее и увереннее. Главное – поверить в силы маленького человека, быть терпеливым, и тогда делить числа методом столбца станет интересным занятием для школьника.

Источник

Деление в столбик

О чем эта статья:

3 класс, 4 класс

Как правильно делить в столбик

Делить столбиком проще, чем высчитывать в уме. Этот способ наглядный, помогает держать во внимании каждый шаг и запомнить алгоритм, который впоследствии будет срабатывать автоматически.

Рассмотрим пример деления трехзначного числа на однозначное 322 : 7. Для начала определимся с терминами:

• 322 — делимое или то, что необходимо поделить;
• 7 — делитель или то, на что нужно поделить:
• частное — результат действия.

Шаг 1. Слева размещаем делимое 322, справа делитель 7, между ставим уголок, а частное посчитаем и запишем под делителем.

Шаг 2. Смотрим на делимое слева направо и находим ту часть, которая больше делителя. 3, 32 или 322? Нам подходит 32. Теперь нужно определить сколько раз наш делитель 7 содержится в числе 32. Похоже, что четыре раза.

Проверяем: 4 × 7 = 28, а 28

Шаг 3. Остаток равен 4. Для продолжения решения его нужно увеличить. Мы сделаем это за счет следующей цифры делимого. Приписываем к четверке оставшуюся двойку и продолжаем размышлять.

Шаг 4. Сколько раз делитель 7 содержится в числе 42? Кажется, шесть раз. Проверяем: 7 × 6 = 42, 42 = 42 — все верно. Записываем полученное число к четверке справа — это вторая цифра частного. Делаем вычитание в столбик 42 из 42, в остатке получаем 0. Значит, числа разделились нацело.

Мы закончили решать пример и в результате получили целое число 46.

Как выглядит деление в столбик с остатком

Это такое же деление, только в результате получается неровное число, как получилось в примере выше.

• Например, делим 19 на 5. Наибольшее число, делящееся на 5 до 19 это 15. Проверяем 5*3=15, 19-15=4. Ответ: 3 и остаток 4. Записываем так: 19:5=3(4).
• Еще пример: делим 29 на 6. Также определяем максимальное число, делящееся на 6 до 29. Подходит 24. Ответом будет: 4 и остаток 5. А записываем: 29:6=4(5).

Примеры на деление в столбик

Давайте закрепим знания на практике. Для этого разделите столбиком примеры ниже, а после проверьте полученные цифры — чур, не подглядывать!

Источник

Деление натуральных чисел столбиком: правило, примеры

Однозначные натуральные числа легко делить в уме. Но как делить многозначные числа? Если в числе уже более двух разрядов, устный счет может занять много времени, да и вероятность ошибки при операциях с многоразрядными числами возростает.

Деление столбиком — удобный метод, часто применяемый для операции деления многозначных натуральных чисел. Именно этому методу и посвящена данная статья. Ниже мы рассмотрим, как выполнять деление столбиком. Сначала рассмотрим агоритм деления в столбик многозначного числа на однозначное, а затем — многозначного на многозначное. Помимо теории в статье приведены практические примеры деления в столбик.

Запись чисел при делении столбиком

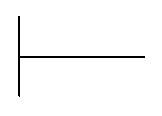
Удобнее всего вести записи на бумаге в клетку, так как при расчетах разлиновка не даст вам запутаться в разрядах. Сначала делимое и делитель записываются слева направо в одну строчку, а затем разделяются специальным знаком деления в столбик, который имеет вид:

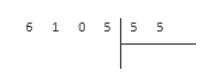
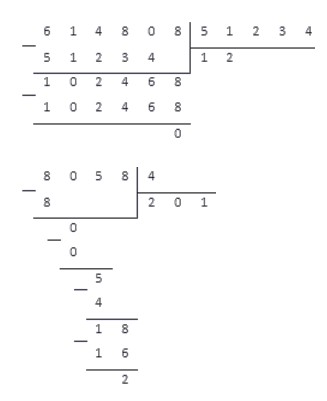
Пусть нам нужно разделить 6105 на 55 , запишем:

Промежуточные вычисление будем записывать под делимым, а результат запишется под делителем. В общем случае схема деления столбиком выглядит так:

Следует помнить, что для вычислений понадобится свободное место на странице. Причем, чем больше разница в разрядах делимого и делителя, тем больше будет вычислений.

Например, для деления чисел 614 808 и 51 234 понадобится меньше места, чем для деления числа 8 058 на 4. Несмотря на то, что во втором случае числа меньше, разница в числе их разрядов больше, и вычисления будут более громоздкими. Проиллюстрируем это:

Деление столбиком на однозначное число

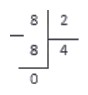
Практические навыки удобнее всего отрабатывать на простых примерах. Поэтому, разделим числа 8 и 2 в столбик. Конечно, данную операцию легко произвести в уме или по таблице умножения, однако провести подробный разбор будет полезно для наглядности, хоть мы и так знаем, что 8 ÷ 2 = 4 .

Итак, сначала запишем делимое и делитель согласно методу деления в столбик.

Следующим шагом нужно выяснить, сколько делителей содержит делимое. Как это сделать? Последовательно умножаем делитель на 0 , 1 , 2 , 3 . . Делаем это до тех пор, пока в результате не получится число, равное или большее, чем делимое. Если в результате сразу получается число, равное делимому, то под делителем записываем то число, на которое умножали делитель.

Иначе, когда получается число, большее чем делимое, под делителем записываем число, вычисленное на предпоследнем шаге.На место неполного частного записываем то число, на которое умножался делитель на предпоследнем шаге.

Вернемся к примеру.

2 · 0 = 0 ; 2 · 1 = 2 ; 2 · 2 = 4 ; 2 · 3 = 6 ; 2 · 4 = 8

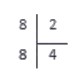
Итак, мы сразу получили число, равное делимому. Записываем его под делимым, а число 4 , на которое мы умножали делитель, записываем на место частного.

Теперь осталось вычесть числа под делителем (также по методу столбика). В нашем случае 8 — 8 = 0 .

Данный пример — деление чисел без остатка. Число, получащееся после вычитания — это остаток деления. Если оно равно нулю, значит числа разделились без остатка.

Теперь рассмотрим пример, когда числа делятся с остатком. Разделим натуральное число 7 на натуральное число 3 .

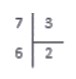
В данном случае, последовательно умножая тройку на 0 , 1 , 2 , 3 . . получаем в результате:

3 · 0 = 0 7 ; 3 · 1 = 3 7 ; 3 · 2 = 6 7 ; 3 · 3 = 9 > 7

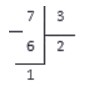
Под делимым записываем число , полученное на предпоследнем шаге. По делителем записываем число 2 — неполное частное, полученное на предпоследнем шаге. Именно на двойку мы умножали делитель, когда получили 6 .

В завершение операции вычитаем 6 из 7 и получаем:

Данный пример — деление чисел с остатком. Неполное частное равно 2 , а остаток равен 1 .

Теперь, после рассмотрения элементарых примеров, перейдем к делению многозначных натуральных чисел на однозначные.

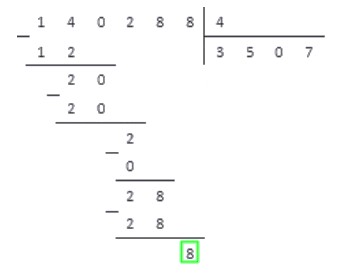
Алгоритм деления столбиком будем рассматривать на примере деления многозначного числа 140288 на число 4 . Сразу скажем, что понять суть метода гораздо легче на практических примерах, и данный пример выбран не случайно, так как иллюстрирует все возможные нюансы деления натуральных чисел столбиком.

Алгоритм деления столбиком

1. Запишем числа вместе с символом деления столбиком. Теперь смотрим на первую слева цифру в записи делимого. Возможны два случая: число, определяемое этой цифрой, больше, чем делитель, и наоборот. В первом случае мы работаем с этим числом, во втором — дополнительно берем следующую цифру в записи делимого и работаем с соответствующим двузначным числом. Согласно с этим пунктом, выделим в записе примера число, с которым будем работать первоначально. Это число — 14 , так как первая цифра делимого 1 меньше, чем делитель 4 .

2. Определяем, сколько раз числитель содержится полученном числе. Обозначим это число как x = 14 . Последовательно умножаем делитель 4 на каждый член ряда натуральных чисел ℕ , включая нуль : 0 , 1 , 2 , 3 и так далее. Делаем это, пока не получим в результате x или число, большее чем x . Когда в результате умножения получается число 14 , записываем его под выделенным числом по правилам записи вычитания в столбик. Множитель, на который умножался делитель, записываем под делителем. Если в результате умножения получается число, большее чем x , то под выделенным числом записываем число, полученное на предпоследнем шаге, а на место неполного частного (под делителем) пишем множитель, на который на предпоследнем шаге проводилось умножение.

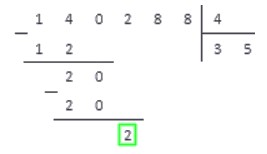
В соответствии с алгоритмом имеем:

4 · 0 = 0 14 ; 4 · 1 = 4 14 ; 4 · 2 = 8 14 ; 4 · 3 = 12 14 ; 4 · 4 = 16 > 14 .

Под выделенным числом записываем число 12 , полученное на предпоследнем шаге. На место частного записываем множитель 3 .

3. Столбиком вычитаем из 14 12 , результат записываем под горизонтальной чертой. По аналогии с первым пунктом сравниваем полученное число с делителем.

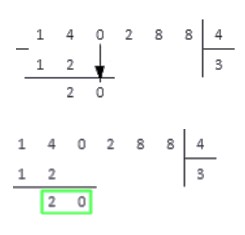
4. Число 2 меньше числа 4 , поэтому записываем под горизонтальной чертой после двойки цифру,расположенную в следующем разряде делимого. Если же в делимом более нет цифр, то на этом операция деления заканчивается. В нашем примере после полученного в предыдущем пункте числа 2 записываем следующую цифру делимого — 0 . В итоге отмечаем новое рабочее число — 20 .

Пункты 2 — 4 повторяются циклически до окончания операции деления натуральных чисел столбиком.

2. Снова посчитаем, сколько делителей содержится в числе 20 . Умножая 4 на 0 , 1 , 2 , 3 . . получаем:

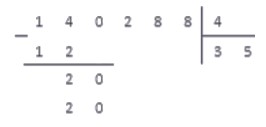
Так как мы получили в результе число, равное 20 , записываем его под отмеченным числом, а на месте частного, в следубщем разряде, записываем 5 — множитель, на который проводилось умножение.

3. Проводим вычитание столбиком. Так как числа равны, получаем в результате число ноль: 20 — 20 = 0 .

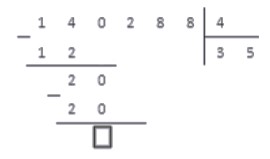
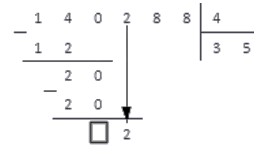
4. Мы не будем записывать число ноль, так как данный этап — еще не окончание деления. Просто запомним место, куда мы могли его записать и запишем рядом число из следующего разряда делимого. В нашем случае — число 2 .

Принимаем это число за рабочее и снова выполняем пункты алгоритма.

2. Умножаем делитель на 0 , 1 , 2 , 3 . . и сравниваем результат с отмеченным числом.

4 · 0 = 0 2 ; 4 · 1 = 4 > 2

Соответственно, под отмеченным числом записываем число 0 , и под делителем в следующий разряд частного также записываем 0 .

3. Выполняем операцию вычитания и под чертой записываем результат.

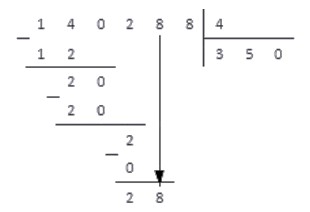
4. Справа под чертой добавляем цифру 8 , так как это следующая цифра делимого числа.

Таким образом, получаем новое работчее число — 28 . Снова повторяем пункты алгоритма.

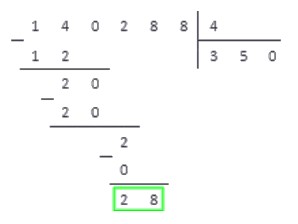
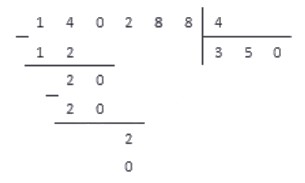
Проделав все по правилам, получаем результат:

Переносим под черту вниз последнюю цифру делимого — 8 . В последний раз повторяем пункты алгоритма 2 — 4 и получаем:

В самой нижней строчке записываем число 0 . Это число записывается только на последнем этапе деления, когда операция завершена.

Таким образом, результатом деления числа 140228 на 4 является число 35072 . Данный пример разобран очень подробно, и при решении практических заданий расписывать все действия столь досканально не нужно.

Приведем другие примеры деления чисел в столбик и примеры записи решений.

Пример 1. Деление натуральных чисел в столбик

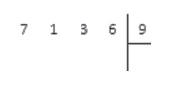
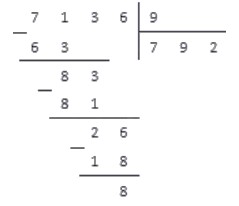
Разделим натуральное число 7136 на натуральное число 9 .

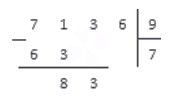
После второго, третьего и четвертого шага алгоритма запись примет вид:

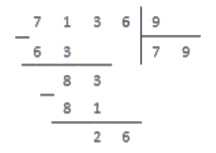
Последний проход, и поучаем результат:

Ответ: Неполное неполное частное чисел 7136 и 9 равно 792 , а остаток равен 8 .

При решении практических примеров в иделе вообще не использовать пояснения в виде словесных комментариев.

Пример 2. Деление натуральных чисел в столбик

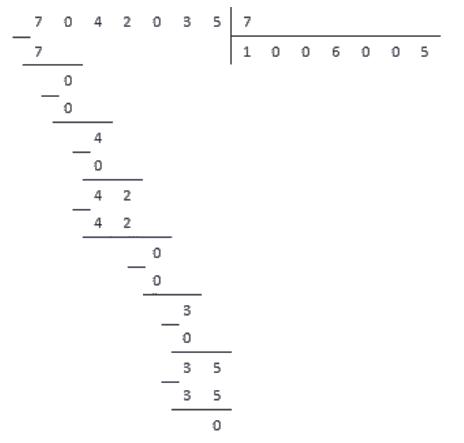
Разделим число 7042035 на 7 .

Деление многозначных натуральных чисел столбиком

Алгоритм деления многозначных чисел в столбик очень похож на рассмотренный ранее алгорим деления многозначного числа на однозначное. Если быть точнее, изменения касаются только первого пункта, а пункты 2 — 4 остаются неизменными.
Если при делении на однозначное число мы смотрели только на первую цифру делимого, то теперь будем смотреть на столько цифр, сколько есть в делителе.Когда число, определяемое этими цифрами, больше делителя, принимам его за рабочее число. Иначе — добавляем еще одну цифру из следующего разряда делимого. Затем следуем пунктам описанного выше алгоритма.

Рассмотрим применение алгоритма деления многозначных чисел на примере.

Пример 3. Деление натуральных чисел в столбик

Разделим 5562 на 206 .

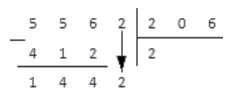
В записи делителя участвуют три знака, поэтому в делимом сразу выделим число 556 .
556 > 206 , поэтому принимаем это число за рабочее и переходим к пункту 2 аглоритма.
Умножаем 206 на 0 , 1 , 2 , 3 . . и получаем:

206 · 0 = 0 556 ; 206 · 1 = 206 556 ; 206 · 2 = 412 556 ; 206 · 3 = 618 > 556

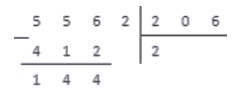
618 > 556 , поэтому под делителем записываем результат предпоследнего действия, а под делимым — множитель 2

Выполняем вычитание столбиком

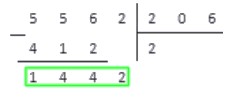
В результате вычитания имеем число 144 . Справа от результата под чертой записываем число из соответствующего разряда делимого и получаем новое рабочее число — 1442 .

Повторяем с ним пункты 2 — 4 . Получаем:

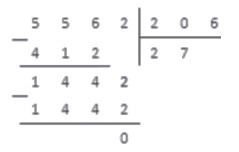
206 · 5 = 1030 1442 ; 206 · 6 = 1236 1442 ; 206 · 7 = 1442

Под отмеченным рабочим числом записываем 1442 , а в следующий разряд частного записываем цифру 7 — множитель.

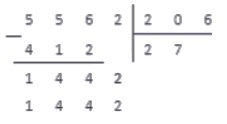
Выполняем вычитание в столбик, и понимаем, что на этом операция деления окончена: в делителе более нет цифр, чтобы записать их правее от результата вычитания.

В завершение данной темы приведем еще один пример деления многозначных чисел в столбик, уже без пояснений.

Пример 5. Деление натуральных чисел в столбик

Источник