Декурсивный метод начисления сложных процентов
При долгосрочных финансово-кредитных операциях проценты после очередного периода начисления присоединяются к сумме долга, и в следующем периоде проценты начисляются на общую сумму, т.е. с капитализацией процентов. Такие проценты называются сложными, база для их начисления увеличивается с каждым очередным периодом начисления.
Наращенная сумма за n лет при использовании постоянной годовой ставки сложных процентов iс определяется по формуле
Задача 7
Банк выдал ссуду 500 тыс. р. на 3 года. Определить погашаемую сумму при использовании сложной ставки 18% годовых и сумму процентных денег.
S = 500 000 (1 + 0.18) 3 = 821 516 р.
Процентные деньги = 821 516 – 500 000 = 321 516 р.
Начисление сложных процентов при сроке ссуды более одного года дает большую сумму процентных денег, чем начисление простых процентов.
Если начисление сложных процентов осуществляется несколько раз в году (по месяцам, кварталам, полугодиям), то используется номинальная ставка процентов – годовая ставка, исходя из которой определяется величина ставки процентов, применяемой в каждом периоде начисления.
Наращенная сумма при этом определяется по формуле
S = P (1 + j / m) mn ,
где j – номинальная ставка сложных процентов, десятичная дробь;
m – количество периодов начисления процентов в году;
n – срок ссуды в годах;
j / m – ставка процентов в каждом периоде начисления, десятичная дробь.
Задача 8
Банк ежеквартально начисляет проценты на вклады по номинальной ставке 16% годовых. Определить сумму, полученную вкладчиком через 5 лет, если первоначальная сумма вклада равна 100 тыс. р.
S = 100 000 (1 + 0.16 / 4) 4 х 5 = 219 112.2 р.
Из формулы для наращенной суммы можно определить значение суммы, выдаваемой заемщику, т.е. осуществить дисконтирование суммы S по сложной ставке процентов.
Решите самостоятельно
Задача 9
Определите современную величину суммы 500 тыс. р., которая будет выплачена через 3 года при использовании ставки сложных процентов 20% годовых.
Ответ: 289 351.8 р.
Срок ссуды (из формулы наращенной суммы) определится
n = log (S/P) / log (1+i).
Логарифмы могут браться с любыми равными основаниями.
Задача 10
Банк начисляет сложные проценты по ставке 12% годовых. Определите срок в годах, за который сумма вклада в 25 тыс. руб. вырастет до 40 тыс. р.
Задача 11
Сумма долга удвоилась за 3 года. Определить использованную годовую ставку сложных процентов.
Антисипативный метод начисления простых процентов
(простые учетные ставки)
При использовании учетных ставок сумма процентных денег от предоставления денег в долг определяется исходя из суммы, которая должна быть возвращена, т.е. величиной получаемого кредита считается не получаемая, а наращенная сумма. Процентные деньги, начисленные по учетной ставке, удерживаются непосредственно при выдаче ссуды, а заемщик получает сумму кредита сразу за вычетом процентных денег. Такая операция называется дисконтированием по учетной ставке, а также банковским или коммерческим учетом. Сумма процентных денег, начисленная по учетной ставке, называется дисконтом.
Сумма, получаемая заемщиком, определится по формуле
P = S (1 – n d),
где d –простая учетная ставка;
(1 – n d) – коэффициент дисконтирования по простой учетной ставке.
Из формулы видно, что, в отличие от ссудных ставок, учетные ставки не могут принимать любые значения, коэффициент дисконтирования не может быть отрицательным, т.е. n•d должно быть строго меньше единицы. Значения d, близкие к предельным, на практике не встречаются.
Задача 12
Заемщик берет ссуду на квартал с обязательством возвратить 100 тыс. р. Определить сумму, полученную заемщиком, и величину дисконта, удержанного банком, при учетной ставке 15% годовых.
P = 100 000 (1 – 0.25 х 0.15) = 96 250 р.
Дисконт = S – P = 100 000 – 96 250 = 3 750 р.
Если срок ссуды задан в днях (д), сумма, получаемая заемщиком, определится по формуле
P = S (1 – d • д / K),
где К – количество дней в году (временная база).
Решите самостоятельно
Задача 13
Определить сумму, полученную заемщиком, и величину дисконта, полученного банком, если по договору заемщик должен через 200 дней возвратить 100 тыс. р. при учетной ставке банка 10% годовых и временной базе 360 дней.
Ответ: 94 444.44 р.; 5 555.56 р.
На практике учетные ставки используются при покупке (учете) векселей и других денежных обязательств. В этом случае банк или другое финансовое учреждение до наступления срока по векселю покупает его у владельца (поставщика) по цене, меньшей той суммы, которая должна быть выплачена по нему в конце срока, или, как принято говорить, банк учитывает вексель с дисконтом. Владелец векселя при этом получает деньги ранее указанного в векселе срока за вычетом дохода банка в виде дисконта. Банк, получив при наступлении срока оплаты векселя указанную в нем сумму, реализует (получает) дисконт.
Указанную операцию можно рассматривать как выдачу банком ссуды в размере суммы, указанной в векселе, по учетной ставке, используемой при его учете, на срок, равный сроку от даты учета до даты погашения векселя. Следовательно, сумма, выдаваемая владельцу учитываемого векселя, будет определяться по формуле
P = S (1 – Δn·d) = S (1 – d·Δд / K),
где Δn = Δд / K – срок в днях от даты учета до даты погашения векселя;
Δд – число дней от даты учета до даты погашения векселя.
Задача 14
При учете векселя на сумму 100 тыс. р., до срока оплаты которого осталось 80 дней, банк выплатил его владельцу 98 тыс. р. Определить, какую учетную ставку использовал банк при временной базе 360 дней.
d = (100 000 – 98 000) х 360 / (100 000 х 80) = 0.09 = 9%.
Решите самостоятельно
Задача 15
Вексель на сумму 200 тыс. р. учет в банке за 30 дней до срока его погашения по учетной ставке 15% годовых. Определить сумму, полученную владельцем векселя, и сумму дисконта, полученную банком, при временной базе 360 дней.
Ответ: 197 500 р.; 2 500 р.
Задача 16
Банк выдает ссуды по учетной ставке 15% годовых. Определить срок ссуды в годах, если заемщик хочет получить 500 тыс. р., а погашаемая сумма должна составить 550 тыс. р
Источник
Начисление сложных процентов



Сложные проценты ( или «проценты на проценты») – это метод расчета дохода кредитора, при котором процентный платеж в каждом расчетном периоде добавляется к капиталу предыдущего периода, а в следующем периоде проценты начисляются уже на наращенный капитал.
В этом случае происходит капитализация процентов, т. е. присоединение начисленных процентов к их базе и, следовательно, база, с которой начисляются проценты, все время возрастает.
Если процентный платеж начисляется и добавляется к капиталу один раз в год, то считается, что капитализация является годовой.
Если процентный платеж начисляется и добавляется к капиталу каждые 6 месяцев, то это называется полугодовой капитализацией.
Начисление сложных процентов и их капитализация может производится поквартально, каждый месяц и т.д.
Существуют два способа начисления сложных процентов: антисипативное (предварительное) и декурсивное (последующее).
Антисипативное начисление сложных процентов – это начисление процентов в начале каждого расчетного периода. Этот способ используется в период высокой инфляции.
Декурсивное начисление сложных процентов – это начисление процентов в конце каждого расчетного периода. Это наиболее распространенный способ начисления сложных процентов.
При декурсивном способе расчета конечная стоимость капитала может быть рассчитана по следующей формуле:
Fn = P * (1 + r) n
где Fn — конечная стоимость капитала
P — первоначальная стоимость капитала
r – процентная ставка, выраженная в десятичных дробях
n – число периодов начисления
Величина (1 + r) называется декурсивным коэффициентом, а n–я степень этого коэффициента – коэффициентом наращивания.
Совокупный процентный платеж при декурсивном начислении можно рассчитать по следующей формуле:
I = P * [ (1 + r) n – 1]
Из выше перечисленных формул можно найти процентную ставку и период:
r = 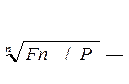
n =(log Fn – log P ) / log ( 1 + r)
При антисипативном начислении сложных процентов конечную сумму капитала можно рассчитать по следующей формуле:
Fn = P * [ 1 / (1 – r)] n
Отсюда при необходимости можно найти I, r, n
I = F – P = P*[ 1 / (1 – r)] n — P = P * ([1 / (1 – r)] n – 1)
Источник
Декурсивный и антисипативный способы начисления процентов
Цена денег – это плата за временное использование «чужих» денег, она определяется в виде простых или сложных процентов. Проценты – это доход от предоставления капитала в долг, то есть денежная плата, взимаемая за использование денег. Если проценты имеют стоимостное выражение, их принято называть процентными деньгами. Давая деньги взаймы сегодня, владелец подвергает себя риску их не возврата, то есть не получения дохода от возможных инвестиций, снижает свою ликвидность. Поэтому он стремится возместить потери – получить доход от предоставления денег в долг. Этот доход и называется процентными деньгами.
Процентная ставка – величина, характеризующая интенсивность начисления процентов.
Период начисленияпроцентов – промежуток времени, за который начисляются проценты (срок, на который предоставляются деньги).
Интервал начисления – минимальный период, по прошествии которого происходит начисление процентов.
Существует два способа начисления процентов: декурсивный и антисипативный.
Декурсивный способ начисления процентов – наращение первоначальной суммы по процентной ставке. Проценты (правильнее – процентные деньги) выплачиваются в конце каждого интервала начисления.
Декурсивная процентная ставка (i), называемая ссудным процентом, – это выраженное в процентах отношение суммы начисленного за определенный интервал дохода I (процентных денег) к сумме, имеющейся на начало данного интервала – P.
Наращение (рост) первоначальной суммы долга – увеличение суммы долга за счет присоединения начисленных процентов.
где S – наращенная сумма.
Коэффициент наращения Кн определяется следующим образом:

Процентная ставка i является относительной величиной, измеряется в долях единицы и определяется делением процентных денег на первоначальную сумму.

Формула расчета процентной ставки идентична расчету статистического показателя «темп прироста».
Определение наращенной суммы S называется компаундингом. Определение первоначальной суммы Р – дисконтированием.
День получения и день окончательного погашения займа считаются одним днем (граничный день). Начисление процентов по кредитам и депозитам происходит, как правило, ежедневно. При этом может использоваться или точное количество дней в году (360/365) или банковское (30 дней).
При антисипативном способе начисления процентов (предварительном)проценты выплачиваются в начале периода, за который начисляются проценты. Пример: проценты, взимаемые банком при учете векселей; по факторинговому кредит и проч. Величиной получаемого кредита является наращенная сумма S. Исходя из нее и начисляются проценты. Заемщик получает сумму кредита за вычетом процентов.
Разница между размером кредита S и выдаваемой суммой Р называется дисконтом, обозначается через D и представляет собой сумму процентных денег.
Ставка дисконта, выраженная в долях от единицы и определяемая делением суммы дисконта на величину Р, называется учетной ставкой d.

Можно заметить, что и сумма процентов I и величина дисконта D определяются одинаковым образом. Однако в первом случае речь идет о приросте текущей стоимости, своего рода «наценке», то есть определяется будущая стоимость «сегодняшних денег». Во втором случае определяется настоящая стоимость будущих денег, то есть определяется «скидка» с будущей стоимости (diskont в переводе с немецкого означает «скидка»).
Чаще всего антисипативный способ используется в чисто технических целях – при дисконтировании, а также при учете векселей в банке и при оплате факторинговых услуг. Во всех остальных случаях в мировой практике более распространен декурсивный способ начисления процентов.
Антисипативный способ применяется в странах с развитой рыночной экономикой в периоды высокой инфляции, так как наращение по антисипативному способу происходит более быстрыми темпами, чем при декурсивном способе начисления.
В хозяйственной практике РБ в настоящее время применяется в основном декурсивный способ начисления простых процентов. Проценты по счетам начисляются в соответствии с договором между банком и клиентом. По счетам учета кредитных и депозитных операций проценты начисляются за период, включающий день выдачи кредита или зачисления денег в депозит, и день, предшествующий погашению кредита или выдачи депозита (закрытия счета). При изменении процентной ставки начисление процентов по новой ставке осуществляется со дня ее установления.
Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций.
Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ — конструкции, предназначенные для поддерживания проводов на необходимой высоте над землей, водой.
Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰).
Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим.
Источник











