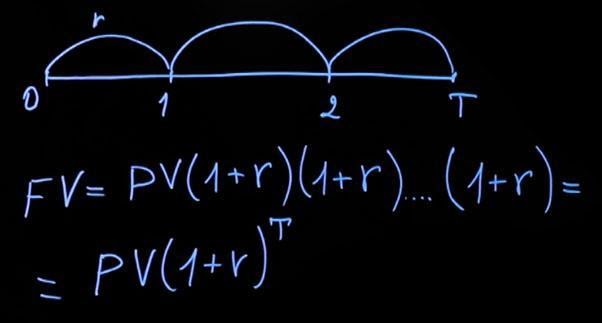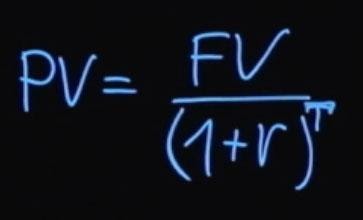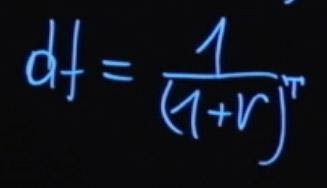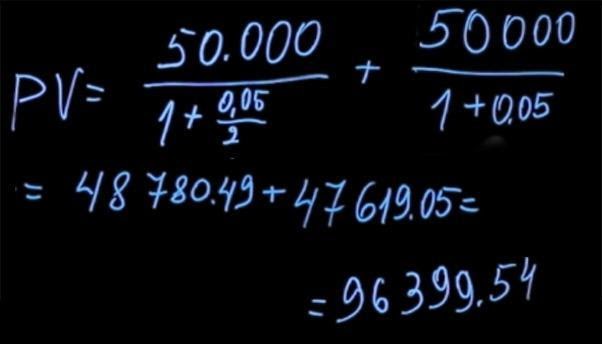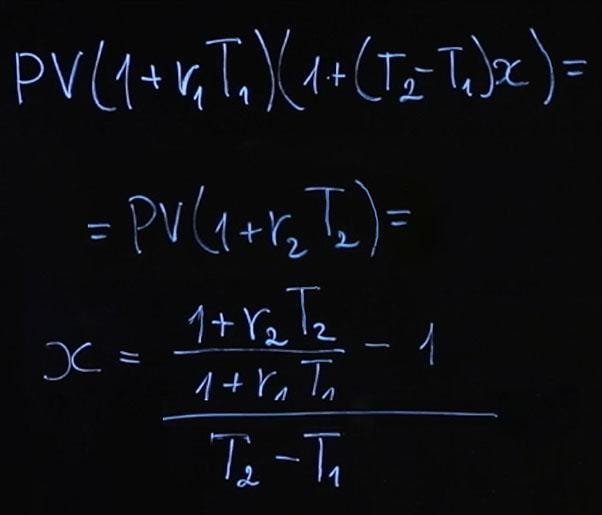Декурсивный способ начисления процентов формула

Декурсивный и антисипативный способы начисления процентов

Цена денег – это плата за временное использование «чужих» денег, она определяется в виде про­стых или сложных процентов. Проценты – это доход от предоставления капитала в долг, то есть денежная плата, взимаемая за использование денег. Если проценты имеют стоимостное выражение, их принято называть процентными деньгами. Давая деньги взаймы сегодня, владелец подвергает себя риску их не возврата, то есть не получения дохода от возможных инвестиций, снижает свою ликвидность. Поэтому он стремится возместить потери – получить доход от предоставления денег в долг. Этот доход и называется процентными деньгами.

Процентная ставка – величина, характеризующая интенсивность начисления процентов.

Период начисленияпроцентов – промежуток времени, за который начисляются проценты (срок, на который предоставляются деньги).

Интервал начисления – минимальный период, по прошествии которого происходит начисление процентов.

Существует два способа начисления процентов: декурсивный и антисипативный.

Декурсивный способ начисления процентов – наращение первоначальной суммы по процентной ставке. Проценты (правильнее – процентные деньги) выплачиваются в конце каждого интервала начисления.

Декурсивная процентная ставка (i), называемая ссудным процентом, – это выраженное в процентах отношение суммы начисленного за определенный интервал дохода I (процентных денег) к сумме, имеющейся на начало данного интервала – P.

Наращение (рост) первоначальной суммы долга – увеличение суммы долга за счет присоединения начисленных процентов.

где S – наращенная сумма.

Коэффициент наращения К_н определяется следующим образом:

. (4.3)

Процентная ставка i является относительной величиной, измеряется в долях единицы и определяется делением процентных денег на первоначальную сумму.

. (4.4)

Формула расчета процентной ставки идентична расчету статистического показателя «темп прироста».

Определение наращенной суммы S называется компаундингом. Определение первоначальной суммы Р – дисконтированием.

День получения и день окончательного погашения займа считаются одним днем (граничный день). Начисление процентов по кредитам и депозитам происходит, как правило, ежедневно. При этом может использоваться или точное количество дней в году (360/365) или банковское (30 дней).

При антисипативном способе начисления процентов (предварительном)проценты выплачиваются в начале периода, за который начисляются проценты. Пример: проценты, взимаемые банком при учете векселей; по факторинговому кредит и проч. Величиной получаемого кредита является наращенная сумма S. Исходя из нее и начисляются проценты. Заемщик получает сумму кредита за вычетом процентов.

Разница между размером кредита S и выдаваемой суммой Р называется дисконтом, обозначается через D и представляет собой сумму процентных денег.

Ставка дисконта, выраженная в долях от единицы и определяемая делением суммы дисконта на величину Р, называется учетной ставкой d.

. (4.6)

Можно заметить, что и сумма процентов I и величина дисконта D определяются одинаковым образом. Однако в первом случае речь идет о приросте текущей стоимости, своего рода «наценке», то есть определяется будущая стоимость «сегодняшних денег». Во втором случае определяется настоящая стоимость будущих денег, то есть определяется «скидка» с будущей стоимости (diskont в переводе с немецкого означает «скидка»).

Чаще всего антисипативный способ используется в чисто технических целях – при дисконтировании, а также при учете векселей в банке и при оплате факторинговых услуг. Во всех остальных случаях в мировой практике более распространен декурсивный способ начисления процентов.

Антисипативный способ применяется в странах с развитой рыночной экономикой в периоды высокой инфляции, так как наращение по антисипативному способу происходит более быстрыми темпами, чем при декурсивном способе начисления.

В хозяйственной практике РБ в настоящее время применяется в основном декурсивный способ начисления простых процентов. Проценты по счетам начисляются в соответствии с договором между банком и клиентом. По счетам учета кредитных и депозитных операций проценты начисляются за период, включающий день выдачи кредита или зачисления денег в депозит, и день, предшествующий погашению кредита или выдачи депозита (закрытия счета). При изменении процентной ставки начисление процентов по новой ставке осуществляется со дня ее установления.

Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ — конструкции, предназначен­ные для поддерживания проводов на необходимой высоте над землей, водой.

Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰).

Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций.

Источник

Декурсивный метод начисления сложных процентов

При долгосрочных финансово-кредитных операциях проценты после очередного периода начисления присоединяются к сумме долга, и в следующем периоде проценты начисляются на общую сумму, т.е. с капитализацией процентов. Такие проценты называются сложными, база для их начисления увеличивается с каждым очередным периодом начисления.

Наращенная сумма за n лет при использовании постоянной годовой ставки сложных процентов i_с определяется по формуле

Задача 7

Банк выдал ссуду 500 тыс. р. на 3 года. Определить погашаемую сумму при использовании сложной ставки 18% годовых и сумму процентных денег.

S = 500 000 (1 + 0.18) 3 = 821 516 р.

Процентные деньги = 821 516 – 500 000 = 321 516 р.

Начисление сложных процентов при сроке ссуды более одного года дает большую сумму процентных денег, чем начисление простых процентов.

Если начисление сложных процентов осуществляется несколько раз в году (по месяцам, кварталам, полугодиям), то используется номинальная ставка процентов – годовая ставка, исходя из которой определяется величина ставки процентов, применяемой в каждом периоде начисления.

Наращенная сумма при этом определяется по формуле

S = P (1 + j / m) mn ,

где j – номинальная ставка сложных процентов, десятичная дробь;

m – количество периодов начисления процентов в году;

n – срок ссуды в годах;

j / m – ставка процентов в каждом периоде начисления, десятичная дробь.

Задача 8

Банк ежеквартально начисляет проценты на вклады по номинальной ставке 16% годовых. Определить сумму, полученную вкладчиком через 5 лет, если первоначальная сумма вклада равна 100 тыс. р.

S = 100 000 (1 + 0.16 / 4) 4 х 5 = 219 112.2 р.

Из формулы для наращенной суммы можно определить значение суммы, выдаваемой заемщику, т.е. осуществить дисконтирование суммы S по сложной ставке процентов.

Читайте также:  Что не является способом образования права ответ

Решите самостоятельно

Задача 9

Определите современную величину суммы 500 тыс. р., которая будет выплачена через 3 года при использовании ставки сложных процентов 20% годовых.

Ответ: 289 351.8 р.

Срок ссуды (из формулы наращенной суммы) определится

n = log (S/P) / log (1+i).

Логарифмы могут браться с любыми равными основаниями.

Задача 10

Банк начисляет сложные проценты по ставке 12% годовых. Определите срок в годах, за который сумма вклада в 25 тыс. руб. вырастет до 40 тыс. р.

Задача 11

Сумма долга удвоилась за 3 года. Определить использованную годовую ставку сложных процентов.

Антисипативный метод начисления простых процентов

(простые учетные ставки)

При использовании учетных ставок сумма процентных денег от предоставления денег в долг определяется исходя из суммы, которая должна быть возвращена, т.е. величиной получаемого кредита считается не получаемая, а наращенная сумма. Процентные деньги, начисленные по учетной ставке, удерживаются непосредственно при выдаче ссуды, а заемщик получает сумму кредита сразу за вычетом процентных денег. Такая операция называется дисконтированием по учетной ставке, а также банковским или коммерческим учетом. Сумма процентных денег, начисленная по учетной ставке, называется дисконтом.

Сумма, получаемая заемщиком, определится по формуле

P = S (1 – n d),

где d –простая учетная ставка;

(1 – n d) – коэффициент дисконтирования по простой учетной ставке.

Из формулы видно, что, в отличие от ссудных ставок, учетные ставки не могут принимать любые значения, коэффициент дисконтирования не может быть отрицательным, т.е. n•d должно быть строго меньше единицы. Значения d, близкие к предельным, на практике не встречаются.

Задача 12

Заемщик берет ссуду на квартал с обязательством возвратить 100 тыс. р. Определить сумму, полученную заемщиком, и величину дисконта, удержанного банком, при учетной ставке 15% годовых.

P = 100 000 (1 – 0.25 х 0.15) = 96 250 р.

Дисконт = S – P = 100 000 – 96 250 = 3 750 р.

Если срок ссуды задан в днях (д), сумма, получаемая заемщиком, определится по формуле

P = S (1 – d • д / K),

где К – количество дней в году (временная база).

Решите самостоятельно

Задача 13

Определить сумму, полученную заемщиком, и величину дисконта, полученного банком, если по договору заемщик должен через 200 дней возвратить 100 тыс. р. при учетной ставке банка 10% годовых и временной базе 360 дней.

Ответ: 94 444.44 р.; 5 555.56 р.

На практике учетные ставки используются при покупке (учете) векселей и других денежных обязательств. В этом случае банк или другое финансовое учреждение до наступления срока по векселю покупает его у владельца (поставщика) по цене, меньшей той суммы, которая должна быть выплачена по нему в конце срока, или, как принято говорить, банк учитывает вексель с дисконтом. Владелец векселя при этом получает деньги ранее указанного в векселе срока за вычетом дохода банка в виде дисконта. Банк, получив при наступлении срока оплаты векселя указанную в нем сумму, реализует (получает) дисконт.

Указанную операцию можно рассматривать как выдачу банком ссуды в размере суммы, указанной в векселе, по учетной ставке, используемой при его учете, на срок, равный сроку от даты учета до даты погашения векселя. Следовательно, сумма, выдаваемая владельцу учитываемого векселя, будет определяться по формуле

P = S (1 – Δn·d) = S (1 – d·Δд / K),

где Δn = Δд / K – срок в днях от даты учета до даты погашения векселя;

Δд – число дней от даты учета до даты погашения векселя.

Задача 14

При учете векселя на сумму 100 тыс. р., до срока оплаты которого осталось 80 дней, банк выплатил его владельцу 98 тыс. р. Определить, какую учетную ставку использовал банк при временной базе 360 дней.

d = (100 000 – 98 000) х 360 / (100 000 х 80) = 0.09 = 9%.

Решите самостоятельно

Задача 15

Вексель на сумму 200 тыс. р. учет в банке за 30 дней до срока его погашения по учетной ставке 15% годовых. Определить сумму, полученную владельцем векселя, и сумму дисконта, полученную банком, при временной базе 360 дней.

Ответ: 197 500 р.; 2 500 р.

Задача 16

Банк выдает ссуды по учетной ставке 15% годовых. Определить срок ссуды в годах, если заемщик хочет получить 500 тыс. р., а погашаемая сумма должна составить 550 тыс. р

Источник

Стоимость денег, типы процентов, дисконтирование и форвардные ставки. Ликбез для гика, ч.1

Представьте себе ситуацию – вы покупаете машину, и вам предлагают два варианта: заплатить с рассрочкой в несколько месяцев или погасить всю сумму сразу и с небольшой скидкой. Какой окажется выгоднее?

Или, например, вы хотите разместить вклад на год. Можно положить на весь срок под высокий процент или на отдельные короткие сроки под более низкий. Что лучше и насколько?

Все ответы под катом. И добро пожаловать в мир, где время — всегда деньги. До этого вы знали об этом, но теперь — в деталях и с примерами.

Меня зовут Мария Абрашкина, я математик и Product Owner в команде по расчету портфельных рисков. А также один из авторов видеокурса про финансовую математику (Ч.1 – Типы начисления процентов, Ч.2 – Дисконтирование, Ч.3 – Форвардные процентные ставки). В этом посте я расскажу о стоимости денег, процентных ставках и облигациях. Эти знания помогут вам в будущем принимать финансовые решения основываясь на точном расчете, используя простую математику.

#1. Временная стоимость денег. Типы начисления процентов

Сначала поговорим о том, что такое временная стоимость денег, или Time Value of Money (TVM), почему деньги имеют стоимость и какие виды процентов существуют.

На картинке ниже показан список фильмов с максимальными кассовыми сборами.

Можем ли мы их сравнить по этим цифрам? Учитывая, что фильмы выходили в разные годы, вряд ли такое сравнение будет правильным. Как быть?

Давайте рассмотрим более простой пример. Допустим, у вас есть тысяча рублей, и я у вас прошу эту сумму в долг. Сколько вы хотите, чтобы я вам отдала через год? Возможно, вы подумаете, что на эту тысячу рублей вы сейчас можете купить бутылку вкусного вина или что-то другое. Также вы можете предположить, что через год на ту же самую тысячу рублей вы вряд ли сможете купить этот товар по причине инфляции. Кроме того, существует риск, что деньги я не верну. Поэтому, скорее всего, вы захотите компенсацию за то, что вы пока не будете покупать бутылку вина или какую-нибудь другую вещь. Также вам необходим стимул, оправдывающий риск того, что деньги я вам могу и не вернуть. Вероятно, вы потребуете от меня вернуть деньги с какой-то надбавкой, то есть с процентом.

Итак, деньги имеют стоимость, потому что их владелец хочет компенсации за то, что он не может купить какой-то товар или услугу, и за риск, который он несет, давая деньги в долг.

На языке математики это будет выглядеть так:

Сейчас вы мне даете тысячу рублей. Обозначим это как PV (Present Value) . Допустим ставка (r) равна 5%, и деньги вы даете мне сроком на один год. Тогда возвращая деньги FV (Future Value) , мне придется добавить к исходной сумме 50 рублей.

Если записать эту формулу в общем виде, то будущее значение равняется сумме долга, умноженной на единицу плюс процентная ставка.

А что, если начисление процентов происходит не раз в год, а чаще? Или что если проценты начисляются в течение двух, трех, десяти лет? В данном случае нам нужно всегда уточнять, каким образом происходит начисление процентов, в конце срока или с какой-то периодичностью и на сколько лет.

Простые проценты

Рассмотрим пример, когда проценты начисляются в конце срока вклада. Будущее значение будет равняться текущему значению плюс текущее значение, умноженное на годовую процентную ставку. Годовая процентная ставка будет прибавляться к сумме нашего вклада столько раз, на сколько лет мы сделали вклад.

Если же процентная ставка начисляется каждый год, то формула будет выглядеть иначе.

Рассмотрим ситуацию с начислением за период в несколько лет. Считаем, что действующая процентная ставка на протяжении всего периода будет одинаковая. Тогда формула принимает следующий вид: текущее значение, умноженное на сумму единица плюс процентная ставка, затем еще раз на сумму единицы и процентной ставки и т. д. Умножать следует столько раз, на какое количество лет был сделан вклад. В общем виде формула будет выглядеть следующим образом:

Обратите внимание – если в первом случае к нашему вкладу каждый год прибавлялась сумма процентов (как в первом примере, где добавлялось к сумме вклада 50 рублей), то в случае с ежегодным начислением на 50 рублей, добавленные в первом периоде, у нас каждый раз начисляется процент.

Всегда важно обращать внимание на то, каким образом происходит начисление процентов. Проценты могут начисляться не только раз в год, но и раз в полгода, каждый день. И в принципе нам ничего не мешает начислять эти проценты непрерывно.

Непрерывное начисление процентов

Давайте рассмотрим, как будет выглядеть формула для начислений процентов чаще одного раза в год. В этом случае будущее значение будет равняться текущему значению, умноженному на сумму единица плюс годовая процентная ставка, деленная на количество периодов начислений в году (n) в степени nT . Если начисления производятся каждые полгода, то n=2 , если каждый день, то n=365 .

Как же будет выглядеть формула, если мы хотим начислять проценты непрерывно? Тут придется вспомнить школьную математику. Формула будет следующей:

Для того, чтобы привести наш предел к какому-то удобному виду, нам нужно сделать подстановку. В итоге мы получаем следующее:

С учетом того, что наш предел равен числу Эйлера (е=2,71), наша формула преобразуется в очень простое выражение. Текущее значение нашего вклада умножается на экспоненту, которая возводится в степень, представленную произведением процентной ставки и количества лет, на которые начисляются наши проценты.

Давайте сравним, как выглядят платежи в зависимости от периодичности начислений. В таблице представлено будущее значение вклада в сто тысяч рублей, который положен на десять лет по ставке двадцать процентов.

Таким образом сумма вклада при начислении процентов ежегодно в два раза превышает сумму вклада при выплате процентов единожды в конце срока.

Если же начисления производятся непрерывно, то сумма вклада оказывается более 700 тысяч рублей против 300 тысяч рублей при простом начислении процентов.

На графике ниже наглядно показано, как растет итоговая сумма вкладов при разных способах начисления процентов.

Отсюда необходимо сделать вывод:

выбирая вклад, важно смотреть не только на размер процентной ставки, но и на периодичность начисления процентов. Высокая процентная ставка не всегда является по-настоящему выгодной.

Поэтому, перед тем как сделать свой выбор, имеет смысл сделать небольшие вычисления, чтобы узнать итоговую сумму вклада при заданных условиях.

#2. Дисконтирование (помогает понять, что лучше: взять рассрочку или заплатить сейчас со скидкой)

Мы рассмотрели, какие бывают ставки и какие бывают способы начисления процентов. Если проценты выплачиваются в конце срока действия вклада, проценты называются простыми, если проценты выплачиваются с какой-то периодичностью, то такие проценты называются сложными.

Давайте решим обратную задачу. Допустим, мы знаем, сколько нам заплатят в будущем (например, нам кто-то пообещал платеж за какой-то продукт). Мы также знаем, какая сейчас процентная ставка. Как нам посчитать текущую цену этого продукта?

Как было сказано ранее, будущее значение суммы платежа будет равняться текущему значению, умноженному на единицу плюс процентная ставка. Если из этой формулы мы выразим текущее значение, то оно будет равняться будущему значению, деленному на единицу плюс процентная ставка.

Если проценты начисляются с какой-то периодичностью, то в общем виде формула выглядит так:

T – это количество периодов выплат начислений процентной ставки. Такой процесс деления будущего значения на единицу плюс процентная ставка в степени T называется дисконтированием. А множитель, единица деленная на сумму единицы плюс r в степени T , называется коэффициентом дисконтирования.

Давайте вернемся к задаче о том, какую премию лучше выбрать. В зависимости от способа премирования сумма выплат может отличаться. При этом не всегда очевидно, какой из способов предпочтительнее. Чтобы дать правильный ответ, необходимо решить математическую задачу. Предположим, у нас есть возможность взять в конце года 105 тысяч рублей при процентной ставке 5 процентов. Либо мы можем выбрать другой способ премирования, когда нам выплачивают по 50 тысяч рублей раз в полгода при той же процентной ставке.

Сравним эти два платежа. Для этого посчитаем, какое будет текущее значение для каждой из данных выплат. Воспользовавшись формулой для нахождения текущего значения, нам нужно продисконтировать 105 тысяч по ставке пять процентов (в данном случае T=1). Получаем 100 тысяч.

Чтобы найти текущее значение выплат через каждые полгода, мы должны 50 тысяч рублей (которые получим через полгода) продисконтировать по ставке два с половиной процента (потому что начисление происходит только в первые полгода. Строго говоря, ставка на 6 мес не равна половине годовой ставки. N(1+x)(1+x)=N(1+0.05) => x=2.4695% мы инвестируем на 6 мес, а потом опять на 6 и это идентично инвестиции на год), пять процентов годовых, деленные на два, плюс 50 тысяч полученные в конце года, которые мы дисконтируем по ставке 5 процентов. В результате подсчетов мы получаем цену первого платежа за полгода в размере 48780 рублей 49 копеек и второго платежа — 47619 рублей 5 копеек. Сумма ценностей составляет 96399 рублей 54 копеек.

Выгоднее получить премию в 105 тыс рублей, подождав дольше.

Например, когда вам предлагают купить автомобиль в рассрочку или заплатить полную сумму сейчас с какой-нибудь скидкой. Нужно взять будущую сумму, которую вы заплатите, привести к текущему значению, а затем сравнивать платежи, происходящие в один и тот же момент времени.

В таком случае сравнение будет корректным.

#3. Форвардные процентные ставки

Допустим, мы с вами договоримся о процентной ставке. Под эту процентную ставку я через год возьму у вас деньги в долг, которые верну через два года плюс процент. Какова должна быть в данном случае процентная ставка, чтобы она была справедливой? Распишем этот пример подробнее.

Мы находимся сейчас в моменте времени «ноль». Через год я у вас по ставке x возьму деньги и верну их вам через два года. Как рассчитать ставку x ? У нас есть несколько опций. Вы можете сейчас положить деньги по ставке r ₁ на год, а затем реинвестировать их по ставке x .

Либо положить деньги сразу по ставке r ₂ на два года.

На финансовом рынке существует правило отсутствия арбитража (No-Arbitrage Condition). Оно говорит о том, что если в конце срока мы получаем одинаковые выплаты, то для инструментов с одинаковым риском начальная сумма должна быть тоже одинаковая. Давайте распишем и это. Будущее значение первого варианта инвестиции FV ₁ будет равняться текущему значению, умноженному на сумму единицы и rT ₁ (будем считать, что у нас простое начисление процентов).

Момент времени T ₁ у нас равняется одному году. Дальше у нас произойдет реинвестирование суммы, и мы положим на промежуток времени от T ₂— T ₁, умноженную на нашу процентную ставку x . T ₂ – это момент времени, в нашем случае два года.

Либо будущее значение FV ₂ будет равняться текущему значению PV , умноженному на единица плюс r ₂, умноженное на T ₂. Согласно условию отсутствия арбитража FV ₁ должно равняться FV ₂.

Из этого мы получаем следующее:

Формула получилась достаточно громоздкая. Давайте рассчитаем по этой формуле пример, а затем подумаем, что мы можем сделать, чтобы она выглядела проще.

Пусть процентные ставки у нас r ₁=4%; r ₂=6%. В таком случае имеем следующее:

Казалось бы странно, что ставка на два года равняется шести процентам, на год она равняется четырем процентам, а от года до двух мы получаем ставку более семи процентов. Объясняется это так. Поскольку в первый год у нас годовая ставка ниже чем на два года, в следующий год она должна быть выше, чем обе этих ставки. Это необходимо для того, чтобы компенсировать недостаток начисления процентов в первом году, и после реинвестирования можно было бы получить такую же сумму, как при инвестировании на два года по более высокой ставке. Такая ставка называется форвардной процентной ставкой.

Чтобы облегчить себе жизнь, давайте упростим эту формулу. Если мы будем использовать формулу непрерывного начисления процентов ( FV=PVe rT ), то тогда мы можем переписать условие отсутствия арбитража следующим образом:

Если мы возьмем логарифм от обеих сторон нашего равенства и сократим константы, мы получим:

Далее легко найти x:

Согласитесь, такую формулу для будущих процентных ставок использовать гораздо проще и удобнее.

Вы можете задать вопрос – а зачем такой странный продукт и кто им пользуется?

Представьте себе ситуацию, когда у вас или у вашей компании точно будет поступление средств через год. Сейчас вы бы хотели обезопасить себя от риска изменения процентных ставок. Вы понимаете, что через год процентная ставка может увеличиться и стать более выгодной, но также вы понимаете, что она может понизиться. И вам вполне комфортно с действующей на рынке форвардной процентной ставкой. Тогда вы можете заключить контракт, указав в нем, что на те деньги которые поступят в будущем через год, вы заключаете договор по заданной ставке. Ставка фиксируется, и вы больше не переживаете о том, как будут происходить изменения процентных ставок на рынке.

Обратите внимание, что форвардная процентная ставка ни в коем случае не является предсказанием будущей цены. Это абсолютно не значит, что процентные ставки будут равны 7,7% через год, когда мы окажемся в точке T₁. Они могут принимать какое угодно значение, и вот почему. В момент, когда мы рассчитываем форвардную процентную ставку из ставок, действующих на рынке, мы можем сказать, что эта ставка является ожиданием рынка относительно будущих цен. Но к моменту, когда мы перемещаемся в будущее, происходят новые события, добавляется новая информация, и рынок каким-то образом меняется. Поэтому процентные ставки через год не будут совпадать с форвардными ставками, рассчитанными на год сейчас.

Источник