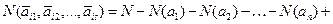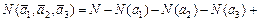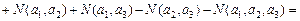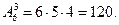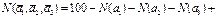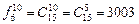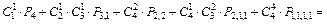Формула включений и исключений
Дата добавления: 2015-07-23 ; просмотров: 7608 ; Нарушение авторских прав
Пусть имеется N предметов и n свойств 
. Каждый из рассматриваемых предметов может обладать одним или несколькими из этих 
свойств. Обозначим через 
число предметов, обладающих свойствами 
(и, быть может, некоторыми другими), а через 
– число предметов, не обладающих свойствами .
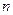
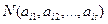
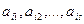
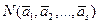
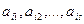
Например,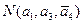 
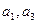
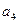
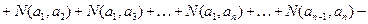
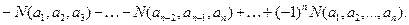
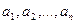
– число предметов, обладающих свойствами 
, но не обладающих свойством 
.
(2.9)
Формула (2.9) называется формулой включений и исключений.Здесь слагаемые включают все комбинации свойств 
без учета их порядка; знак «+» ставится, если число учитываемых свойств чётно, и знак «–», если это число нечётно.
Пример 2.3.8.В результате опроса 70 студентов выяснилось, что 45 из них занимаются спортом, 29 – музыкой, 9 – и спортом и музыкой. Сколько студентов из числа опрошенных не занимаются ни спортом, ни музыкой.
Решение. Чтобы применить формулу (2.9), обозначим через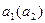 
– свойство студента, состоящее в том, что он занимается спортом (музыкой). Тогда имеем
N=70, N(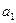 
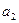
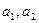
)=45, N( 
)=29, N( 
)=9.
Нужно найти число N(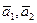 
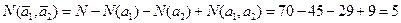
). По формуле (2.2) получаем
.
Пример 2.3.9. В студенческой группе 30 человек. Из них 15 человек знают английский язык, 10 – французский. 6 – немецкий, 5 – английский и французский, 3 – английский и немецкий, 3 – французский и немецкий, 2 – английский, французский и немецкий. Сколько человек в данной группе не знают ни одного языка?
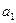
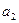
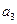
Решение. Обозначим количество студентов в данной группе N и введем три свойства для студентов данной группы: – знать английский язык, – знать французский язык, 
– знать немецкий язык. Тогда
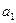
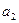
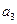
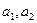
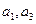
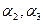
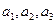
N( )=15, N( )=10, N( )=6, N( 
)=5,
N( 
)=3, N( 
)=3, N( 
)=2.
По формуле включений и исключений находим число студентов в данной группе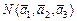 
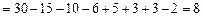
, которые не знают ни одного языка
.
2.4 Примеры решения задач
Задача 1. Имеется 10 билетов денежно-вещевой лотереи и 15 билетов художественной лотереи. Сколькими способами можно выбрать один лотерейный билет?
Решение. Билет денежно-вещевой лотереи можно выбрать 10 способами (все билеты различны), билет художественной лотереи – 15 способами. По правилу суммы выбор одного лотерейного билета можно осуществить 10+15=25 способами.
Задача 2. Сколькими способами из 28 костей домино можно выбрать кость, на которой есть 1 или 2?
Решение. Выбрать кость, содержащую 1, можно 7 способами, содержащую 2 – тоже 7 способами, но среди этих способов есть один общий – это выбор кости 1:2.
Значит, общее число способов выбора нужной кости считается как 7+7-1=13.
Задача 3. Из города А в город В идет 5 дорог, из В в С – 4 дороги. Сколько путей, проходящих через В, ведут из А в С?
Решение. Весь путь из А в С состоит из 2 частей – из А в В и из В в С. Из города А в город В можно выйти 5 способами, из города В в город С – 4 способами. Общее число путей, ведущее из А в С,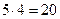 
.
Задача 4. Сколькими способами можно выбрать гласную и согласную букву из букв слова «компьютер»?
Решение. Гласную букву можно выбрать 3-мя способами. После любого выбора гласной согласную можно выбрать 5-ю способами.
По правилу произведения выбор гласной и согласной можно осуществить 15-ю способами.
Задача 5. На втором курсе изучаются 14 предметов. Сколькими способами можно составить расписание занятий на вторник, если в этот день недели должно быть 5 различных пар?
Решение. Различных способов составления расписания, очевидно, столько, сколько существует пятиэлементных упорядоченных подмножеств у четырехзначного множества.
Следовательно, число способов равно число размещений из 14 элементов по 5, т.е. равно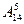 
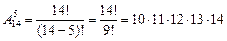
. По формуле (2.4):
.
Задача 6. Сколько шестизначных чисел, кратных пяти, можно составить из цифр 1, 2, 3, 4, 5, 6 при условии, что в числе цифры не повторяются?
Решение. Для того, чтобы число, составленное из заданных цифр, делилось на 5, необходимо и достаточно, чтобы цифра 5 стояла на последнем месте. Остальные пять цифр могут стоять на оставшихся пяти местах в любом порядке. Следовательно, искомое число шестизначных чисел, кратных пяти, равно числу перестановок из пяти элементов, т.е.
.
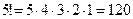
Задача 7. Сколько различных перестановок можно образовать из букв слова «задача»?
Решение. Образовать какую-либо перестановку из букв слова «задача» – это значит на шесть занумерованных мест каким-либо образом поставить одну букву «з», одну букву «д», одну букву «ч» и три буквы «a». Если буквы «з», «д» и «ч» как-то поставлены, то остальные места заполняются буквами «а». Но сколькими способами можно поставить три различных буквы на шесть мест? Очевидно, что число способов равно числу всех трехэлементных упорядоченных подмножеств шестиэлементного множества, т.е равно
Задача 8. Сколько экзаменационных комиссий, состоящих из 7 членов, можно образовать из 14 преподавателей?
Решение. Очевидно, столько, сколько существует семиэлементных подмножеств у четырнадцати элементарного множества. По формуле (2.6) находим:
.
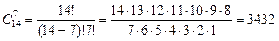
Задача 9. В чемпионате страны по футболу (высшая лига) участвуют 18 команд, причем каждые две команды встречаются между собой 2 раза. Сколько матчей играется в течение сезона?
Решение. В первом круге состоится столько матчей, сколько существует двухэлементных подмножеств у множества, содержащего 18 элементов, т.е. их число равно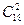 
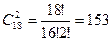
. По формуле (2.6) получаем:
.
Во втором круге играется столько же матчей, поэтому в течение сезона состоится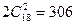 
встреч.
Задача 10. Сколько чисел в первой сотне, которые, не делятся нацело ни на 2, ни на 3, ни на 5?
Решение. Эта задача решается с помощью формулы включения-исключения. Введем обозначения:
– свойство чисел делиться на 2;
– свойство чисел делиться на 3;
– свойства чисел делиться на 5;
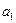
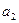
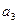
Тогда,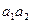 
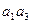
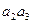
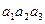
означает, что число делится на 6, 
означает, что число делится на 10, 
означает, что число делится на 15, наконец, 
означает, что число делится на 30.
По формуле включения-исключения имеем
;
; 
; 
; 
; 
;
; 
.
.
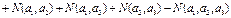
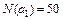
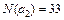
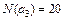
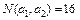
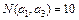
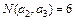
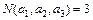
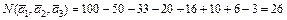
Таким образом, 26 чисел из 100 не делятся ни на 2, ни на 3, ни на 5.
Задача 11. Сколько слов можно составить, переставив буквы в слове «математика»?
Решение. В слове «математика» 3 буквы «a», 2 буквы «м», 2 буквы «т», поэтому число перестановок всех букв разделим на число перестановок повторяющихся букв:
.
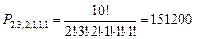
Задача 12. На книжной полке стоят 20 книг по линейной алгебре, 12 – по дискретной математике, 7 – по математическому анализу и 25 – по мировой экономике. Сколькими способами можно выбрать книгу по математике?
Решение. Найдем число способов, которыми можно выбрать книгу по линейной алгебре, или по дискретной математике, или по математическому анализу.
Книгу по линейной алгебре можно выбрать 20 способами, по дискретной математике – 12 способами и по математическому анализу – 7 способами. Эти выборы несовместны.
Поэтому по правилу суммы находим, что выбрать книгу по математике можно N=20+12+7=39 способами.
Задача 13. Сколько трехзначных чисел можно составить из цифр 1, 3, 5, если цифры в числе не повторяются?
Решение. На месте сотен поставим любую из трех цифр. После каждого такого выбора на месте десятков можно поставить любую из оставшихся цифр, так как цифры в числе не повторяются. Наконец, на месте единиц можно поставить оставшуюся одну цифру.
Повторным применением правила произведения найдем число трехзначных чисел, равное
.
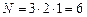
Задача 14. Сколько различных «слов», состоящих не менее из четырех разных букв, можно образовать из букв слова «цветок»?
Решение. Слово «цветок» состоит из шести различных букв. По правилу произведения можно составить
четырехбуквенных слов,
пятибуквенных и
шестибуквенных слов.
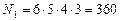
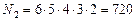
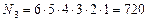
По правилу суммы всего можно составить
слов,
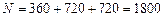
состоящих не менее чем из четырех букв.
Задача 15. Четверо студентов сдают экзамен. Сколькими способами могут быть поставлены им оценки, если известно, что никому из них не будет поставлена неудовлетворительная оценка?
Решение. Каждый из студентов может получить любую из оценок: «отлично», «хорошо», «удовлетворительно». Значит, рассматриваемое множество Х состоит из трех различных элементов. При этом порядок расстановки отметок существенен, отметки могут повторяться, а общее число поставленных отметок равно четырем (например, «отлично», «хорошо», «отлично», «удовлетворительно»).
Следовательно, необходимо составить размещения с повторениями из трех элементов по четыре. А это число равно
.
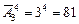
Задача 16. В студенческий научный клуб избрали 9 человек. Из них надо выбрать секретаря и председателя СНК. Сколькими способами можно это сделать?
Решение. Из множества, содержащего 9 различных элементов, выбираются 2 элемента. Порядок существенен (например, выборы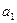 
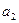
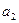
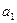
– секретарь, – председатель и – секретарь, – председатель, состоящие из одних и тех же элементов, различны). Элементы не могут повторяться.
Следовательно, необходимо найти число размещений без повторений из девяти элементов по два элемента в каждом, т.е.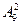 
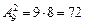
. Значит, секретаря и председателя можно выбрать 
способами.
Задача 17. Имеется 5 различных стульев и 7 рулонов обивочной ткани различных цветов. Сколькими способами можно осуществить обивку стульев?
Решение. Поскольку стулья различны, то мы можем расположить их в определенном порядке. Тогда каждый способ обивки есть по существу кортеж длины 5, составленный из элементов данного множества цветов ткани, содержащего 7 элементов.
Значит, всего способов обивки столько, сколько имеется таких кортежей, т.е. размещений с повторениями из 7 элементов по 5. Воспользовавшись формулой (2.5), находим
.
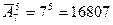
Задача 18. В Российской Федерации для автомобильных номеров используются 10 цифр и 28 букв (кроме ё, й, ь, ъ, ы). Каждый номер состоит из трех букв и трех цифр (кроме сочетания цифр 000). Какое максимальное число машин может получить номера при такой системе?
Решение. Сначала осуществим выбор трех цифр. Каждый такой комплект есть кортеж длины 3, составленный из элементов данного 10-элементного множества цифр, а всего таких кортежей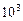 
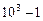
. Если исключить кортеж 000, останется 
кортежей.
Аналогично выбор трех букв из 28 можно осуществить числом способов, равным 28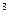 
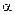
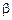
. Пусть 
– комплект цифр, 
– комплект букв.
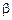
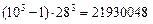
Тогда каждый номер есть по существу пара , а число способов выбора такой пары находится по правилу произведения. Использовав это правило, получим 
номеров машин.
Задача 19. Сколько хорд провести через 6 точек, лежащих на одной окружности?
Решение. Из множества, содержащего 6 различных элементов, выбирают 2 элемента, так как хорда однозначно определяется двумя точками, ледащими на окружности. Порядок элементов роли не играет. Например,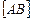 
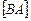
и 
– одна и та же хорда.
Следовательно, необходимо найти число сочетаний из шести элементов по два, т.е.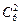 
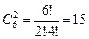
. Значит, можно провести 
различных хорд.
Задача 20. Даны натуральные числа от 1 до 30. Сколькими способами можно выбрать три числа так, чтобы их сумма была четной?
Решение. Сумма трех чисел будет четной, если все слагаемые четные или одно слагаемое четное и два слагаемых нечетные.
Следовательно, из 15 четных чисел 3 числа можно выбрать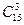 
различными способами, так как порядок слагаемых не учитывается.
Кроме того, из 15 нечетных чисел 2 числа можно выбрать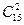 
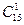
различными способами и после каждого такого выбора по одному четному числу из 15 можно выбрать 
способами.
По правилу произведения число выборок, содержащих два нечетных и одно четное число, равно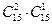 
.
Применяя правило суммы, найдем общее число выборок, удовлетворяющих условию
.
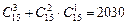
Задача 21. Сколькими способами можно расставить белые фигуры (2 ладьи, 2 слона, 2 коня, ферзь и король) на первой линии шахматной доски?
Решение. Рассматриваемые кортежи имеют длину 8 и состоят из элементов пяти видов. Состав кортежей имеет вид (2,2,2,1,1).
Следовательно, число способов, которыми можно расставить 8 фигур на первой линии шахматной доски, равно
.
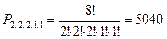
Задача 22. В цветочном магазине продаются цветы шести сортов. Сколько можно составить различных букетов из десяти цветов в каждом? (Букеты, отличающиеся лишь расположением цветов, считаются одинаковыми.)
Решение. Рассматриваемое множество состоит из шести различных элементов, а кортежи имеют длину 10. Поскольку порядок расположения цветов в букете не играет роли, то число букетов равно числу сочетаний с повторениями из шести элементов по десяти в каждом.
Следовательно, можно составить
Задача 23. Сколько имеется перестановок букв в слове excellent?
Решение: В этом слове буквы e встречается трижды, а буква l встречается дважды. Все остальные буквы – x, с, n и t – встречаются по одному разу. По формуле 2.7 число перестановок равно
.
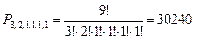
Задача 24.Набор данных содержит результаты 500 наблюдений. Эти данные обрабатываются тремя программами. Все вместе они обрабатывают результаты всех 500 наблюдений, причем каждая из них обрабатывает не менее 100 результатов. В остальном эти результаты разбиваются на группы произвольно. Сколькими способами это можно сделать?
Решение.Используем теорему 1 раздела 2.3.2. Тогда получим
.
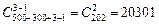
Задача 25.Сколько четырехбуквенных слов можно составить, используя буквы из набора a, a, a, b, b, с, с, с, с, d, d?
Решение: Первый шаг решения задачи состоит в том, чтобы разбить ее на несколько непересекающихся подслучаев. В каждом из них можно будет применить формулу 2.9, а для получения окончательного ответа нужно будет ко всем этим подслучаям применить принцип сложения.
Описания подслучаев и число способов выбора для них приведены в табл.
Таблица 2. 1
| Подслучаи | |||
| Виды букв | Число способов выбрать буквы | Число перестановок букв | |
| (a) | 4–одинаковые |  |  |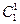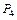
| (b) | 3–одинаковые 1–другая |   |  |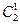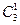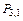
| (c) | 2–пары |  |  |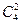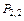
| (d) | 2–одинаковые 2–разные |   |  |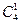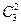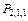
| (e) | 4–разные |  |  |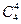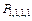
Согласно принципу сложения получается окончательный ответ:
.
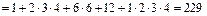
Когда разбиения состоят из множеств фиксированного размера и размеры множеств не все различны, нужно учитывать, что элементы разбиения можно менять местами, и при этом искомое число не изменяется.
Задача 26. Сколькими способами 12 экзаменов можно разбить на три набора по четыре экзамена в каждом?
Решение. По формуле 2.6 получим:
.
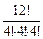
В полученном ответе не учитывается тот факт, что три множества можно менять местами, поэтому окончательный ответ имеет такой вид:
.
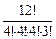
В данной задаче показано, как подсчитывать разбиения неразличимых элементов в множествах, которые сами могут быть неразличимыми.
Источник
